TREES Recursion Review Base Case how we exit

TREES

Recursion Review • Base Case- how we exit and don’t go into infinite recursion • Some work • Division of work • Recursive call (s) • For many of you, recursion is intimidating. Eventually it will become second nature just as loops and file operations have.

Recursive Process • Decide if you want to use recursion • Decide inputs and outputs • Decide how to break down the work • Tentatively decide on a base case • Make recursive calls • Bring back together the results • Return the proper values • Finalize your base case • Trace the recursion

Practice - Sum the numbers from 1 to n int sum(int n){ if(n==1){ return n; } int cur. Sum=n+sum(n-1); return cur. Sum; }

Practice - Sum array int sum( int* arr, int pos, int size){ if(pos==size-1) return arr[pos]; return arr[pos]+sum(arr, pos+1, size); }

Practice - Linked List class Node { public: int value; Node *next; Node( int val, Node *n = NULL ){ value=val; next=n; } };

Practice - Linked List Print Void print(Node* cur){ if( cur==NULL) return; cout<<cur->value; print(cur->next); }

Binary Search Tree • What is a tree? • What is a Binary search tree?

Binary Search Tree • Is a binary tree (each node has two pointers to children) • Ordered to facilitate searching • Anything to the left is a smaller value • Anything to the right is a greater value • Children are binary search trees • Cannot have duplicate values because it violates the search property

Example 1

At your seats • Build a tree from these nodes • B R L M T C A N P D

Deletion • We need to preserve the binary search properties • Deleting a leaf is easy, we can just delete it, and set its parent’s pointer to null • The easiest way to delete a node is to find its successor, copy the value over, then delete that leaf node

Code - Node class Node { public: int value; Node *left; Node *right; Node( int val, Node *l = NULL, Node *r = NULL ){ value=val; left=l; right=r; } };

Code - Search Node* search( int value, Node* cur){ if(cur==NULL) return NULL; else if( value == cur->value) return cur; else if( value < cur->value) return search(value, cur->left); else return search(value, cur->right); }

Code - Delete void delete( int value, Node* cur){ }

Complexity • Search • Insert • Delete

Disadvantages • What is my worst case? When will it occur?

Balanced • Balanced means the heights of the left and right sub-trees differ by at most one • This needs to be true for every node in the tree • If a tree is balanced, what is the worst case?

Balanced Examples

Alternatives • AVL and Splay trees • Self balancing

AVL - Adelson, Velskii, Landis • Binary tree • Balanced • Determining if it is an AVL tree • Check each node for • Right sub-tree is an AVL tree • Left sub-tree is an AVL tree • Heights of right and left differ by at most one • AVL search Tree • An AVL tree, but also a binary tree

AVL practice • Is it AVL? Is it AVL search?

AVL • We usually only look at AVL search • When I say AVL, I mean AVL search • If not search, I will specify by saying non-search AVL

Properties • Height is logn • Can do it for any n • Search is logn • Insertion is logn • Deletion is logn

AVL - Search • How do we search?

AVL - Insert • How is it done?

AVL - Rotations • RR • LL • RL • LR

AVL - Single Left Rotation • Fixes a RR inbalance

AVL - Double Left Rotation • Fixes an RL inbalance

AVL Insert • 3, 2, 1, 4, 5, 6, 7, 16, 15, 14

AVL Delete • How do we delete?

AVL Delete • How do we delete? • Same way as in a binary search tree • But the tree can be thrown off balance • Re- balance the tree using rotations • May need to do multiple rotations.

AVL Delete • Rebalancing • Starting where we deleted, we follow the recursion back up the tree • At every node we visit, we need to check that it is still balanced. • If it is not balanced, we use a rotation to fix it • What is the worst case for the number of rotations I have to do?

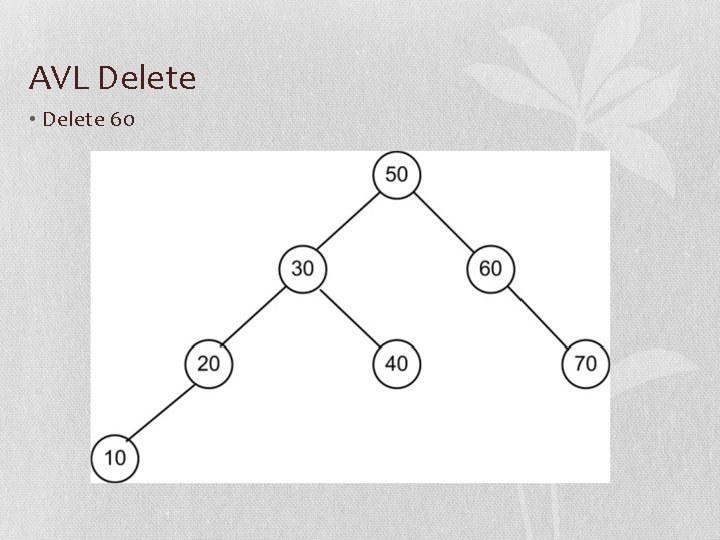
AVL Delete • Delete 60

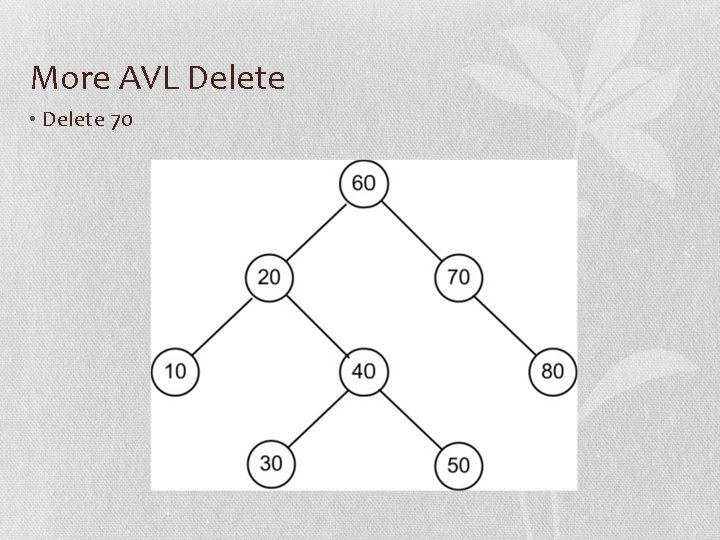
More AVL Delete • Delete 70

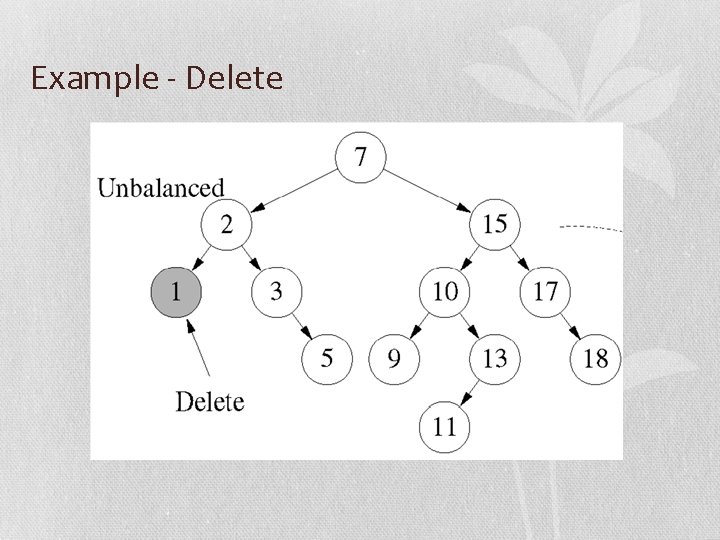
Example - Delete

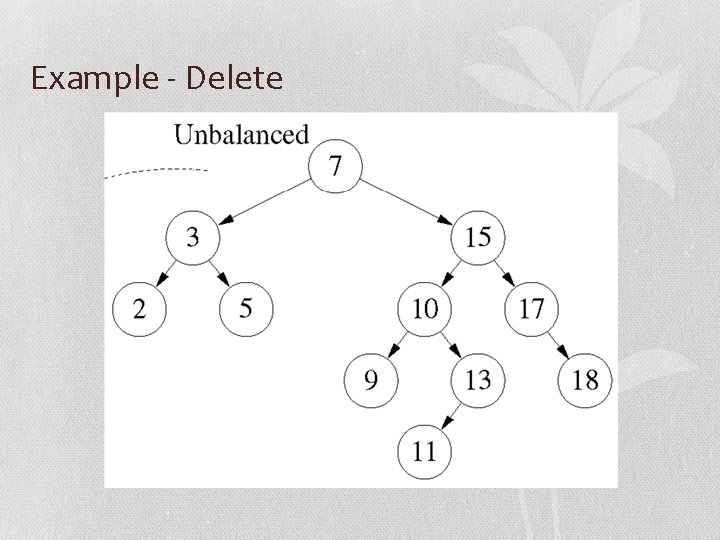
Example - Delete

Example - Delete

Delete – Code? int Delete (){ }

Participation Quiz – 5 points 1) Do you like the way I use power points to guide the lecture? Suggestions? 2) Do you feel I do a good job answering in class questions? Suggestions? 3) Do you find the examples, and asking for class guidance through them helpful? Suggestions? 4) Write a short snipet of code that has O(n) complexity. It can be simple, and does not need to do anything useful. 5) Which trees drawn on the board are AVL? (remember I mean AVL search) I want this to be the best learning experience possible for you, so please include any other comments or suggestions you have for improving the course.