Trees Mammal Dog 2014 Goodrich Tamassia Goldwasser Pig

Trees Mammal Dog © 2014 Goodrich, Tamassia, Goldwasser Pig Trees Cat 1

© 2014 Goodrich, Tamassia, Goldwasser Trees 2

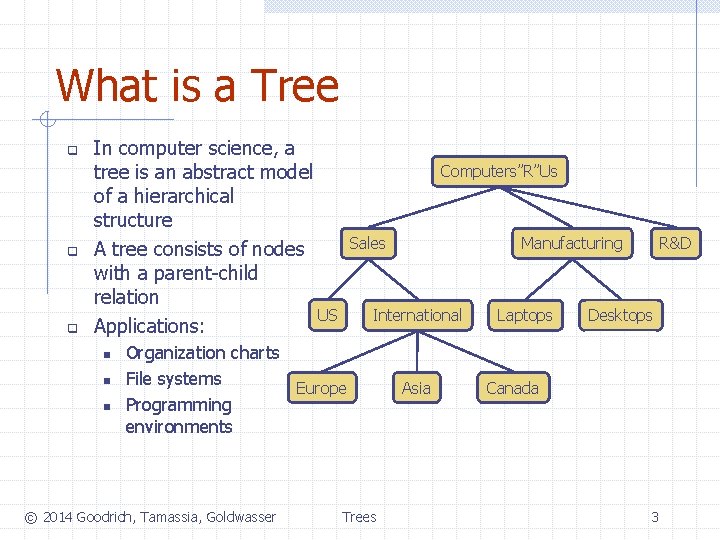
What is a Tree q q q In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes with a parent-child relation US Applications: n n n Computers”R”Us Sales International Organization charts File systems Europe Programming environments © 2014 Goodrich, Tamassia, Goldwasser Manufacturing Trees Asia Laptops R&D Desktops Canada 3

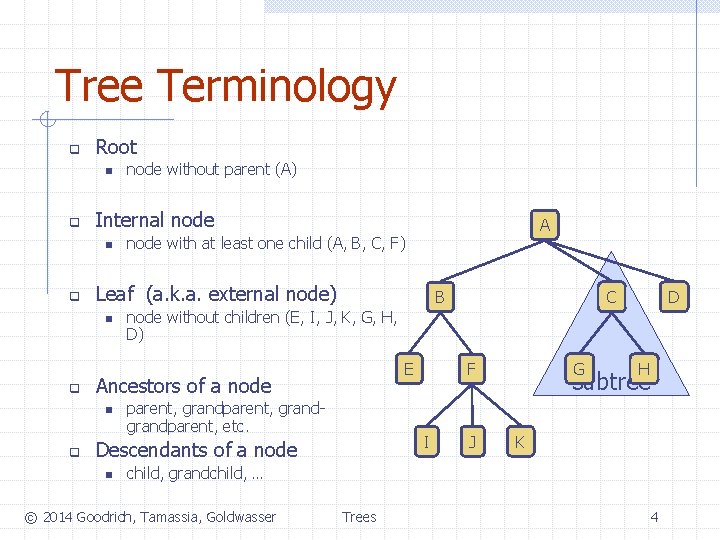
Tree Terminology q Root n q Internal node n q node with at least one child (A, B, C, F) B E parent, grandgrandparent, etc. F I Descendants of a node n C D node without children (E, I, J, K, G, H, D) Ancestors of a node n q A Leaf (a. k. a. external node) n q node without parent (A) J G H subtree K child, grandchild, … © 2014 Goodrich, Tamassia, Goldwasser Trees 4

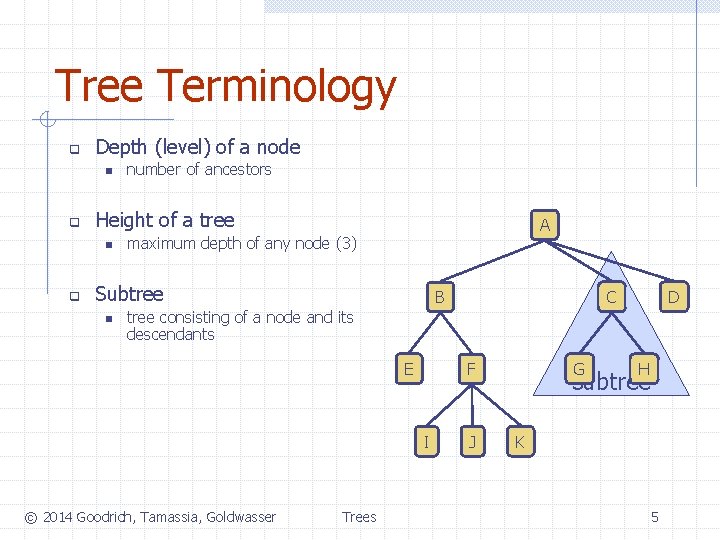
Tree Terminology q Depth (level) of a node n q Height of a tree n q number of ancestors A maximum depth of any node (3) Subtree n B C D tree consisting of a node and its descendants E F I © 2014 Goodrich, Tamassia, Goldwasser Trees J G H subtree K 5

Tree ADT q q We use “positions” to abstract nodes Generic methods: n n q Query methods: n n integer size() boolean is. Empty() n boolean is. Internal(p) boolean is. External(p) boolean is. Root(p) Accessor methods: n n position root() position parent(p) Iterable children(p) integer num. Children(p) © 2014 Goodrich, Tamassia, Goldwasser Additional update methods may be defined by data structures implementing the Tree ADT Trees 6

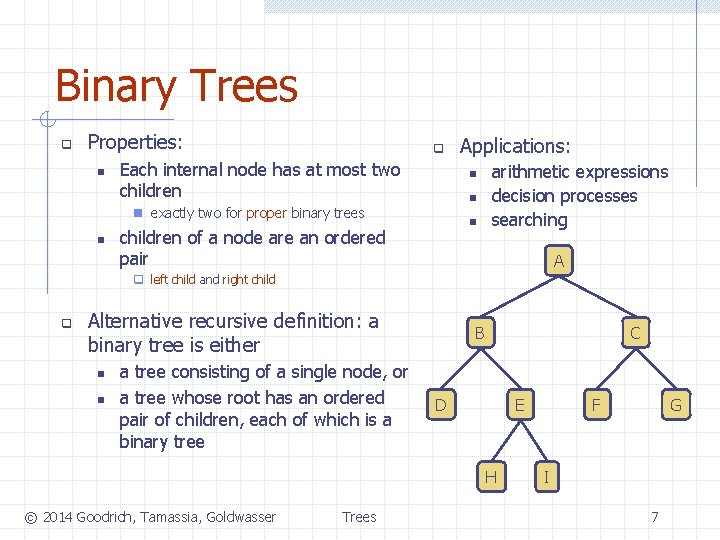
Binary Trees q Properties: n q Each internal node has at most two children n exactly two for proper binary trees n Applications: n children of a node are an ordered pair arithmetic expressions decision processes searching A q left child and right child q Alternative recursive definition: a binary tree is either n n a tree consisting of a single node, or a tree whose root has an ordered pair of children, each of which is a binary tree B C D H © 2014 Goodrich, Tamassia, Goldwasser Trees F E G I 7

Arithmetic Expression Tree q Binary tree associated with an arithmetic expression n n q internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a © 2014 Goodrich, Tamassia, Goldwasser 3 b 1 Trees 8

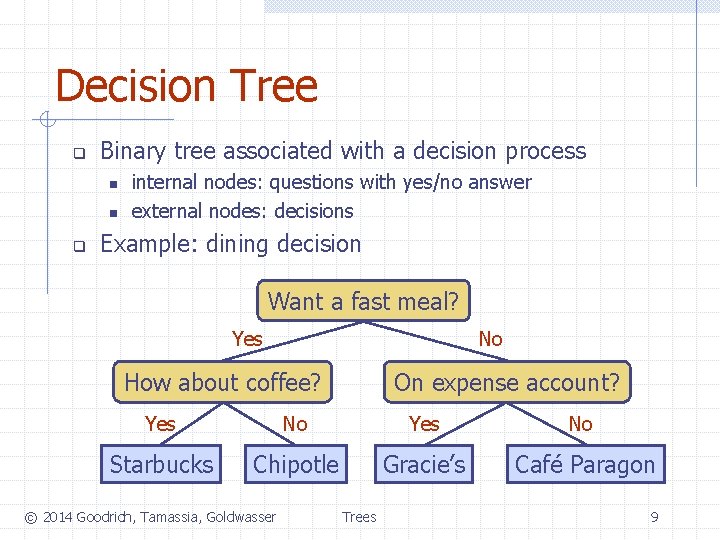
Decision Tree q Binary tree associated with a decision process n n q internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Chipotle Gracie’s Café Paragon © 2014 Goodrich, Tamassia, Goldwasser Trees 9

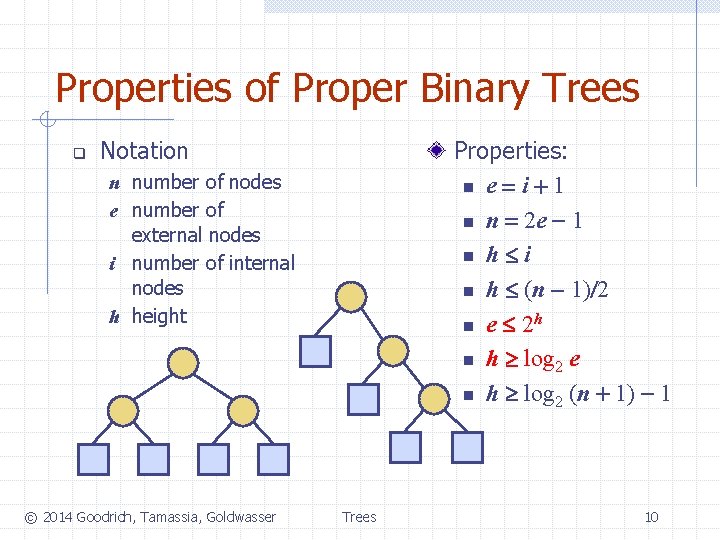
Properties of Proper Binary Trees q Notation Properties: n e = i + 1 n n = 2 e - 1 n h i n h (n - 1)/2 n e 2 h n h log 2 e n h log 2 (n + 1) - 1 n number of nodes e number of external nodes i number of internal nodes h height © 2014 Goodrich, Tamassia, Goldwasser Trees 10

Binary. Tree ADT q q The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT Additional methods: n n n position left(p) position right(p) position sibling(p) © 2014 Goodrich, Tamassia, Goldwasser Trees q q The above methods return null when there is no left, right, or sibling of p, respectively Update methods may be defined by data structures implementing the Binary. Tree ADT 11

Implementing Trees q How to store a tree? © 2014 Goodrich, Tamassia, Goldwasser Trees 12

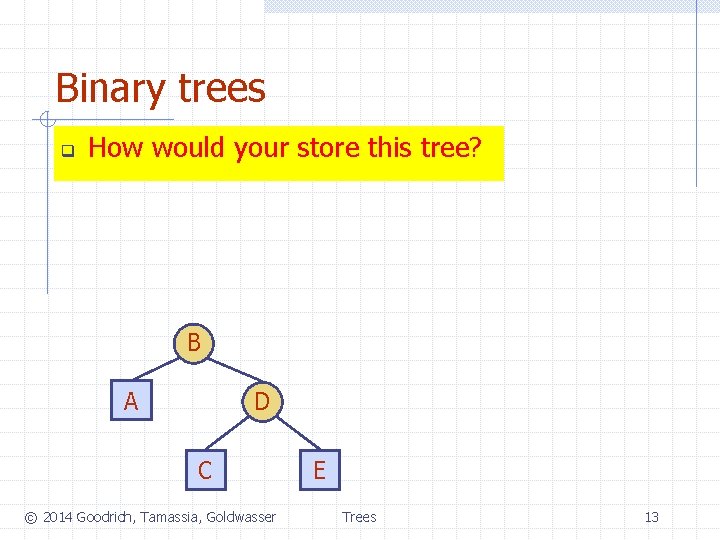
Binary trees q How would your store this tree? B D A C © 2014 Goodrich, Tamassia, Goldwasser E Trees 13

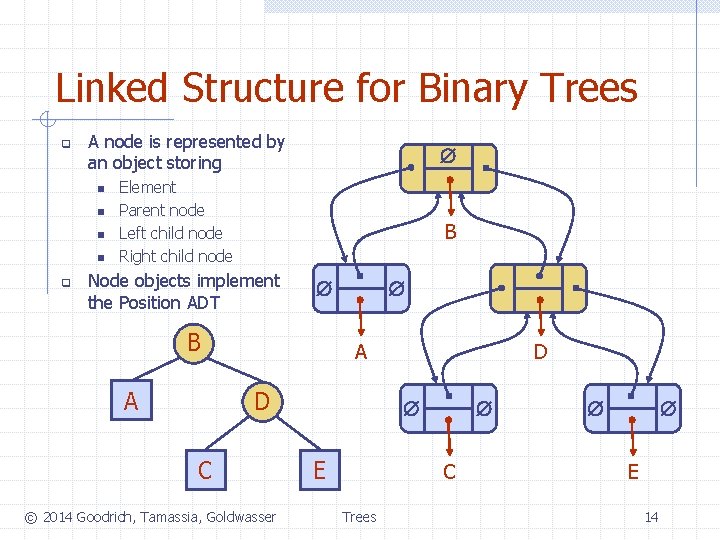
Linked Structure for Binary Trees q A node is represented by an object storing n n q Element Parent node Left child node Right child node B Node objects implement the Position ADT B A D A C © 2014 Goodrich, Tamassia, Goldwasser D E C Trees E 14

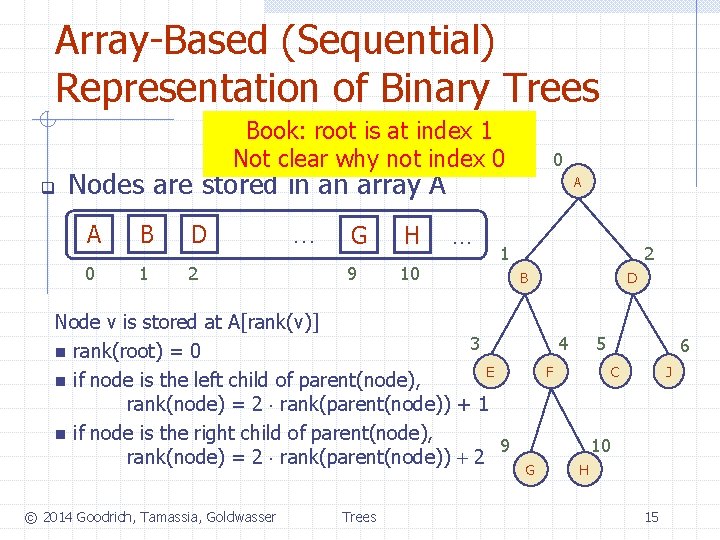
Array-Based (Sequential) Representation of Binary Trees Book: root is at index 1 Not clear why not index 0 q 0 Nodes are stored in an array A A B D 0 1 2 … G H 9 10 A … 1 Node v is stored at A[rank(v)] 3 n rank(root) = 0 E n if node is the left child of parent(node), rank(node) = 2 rank(parent(node)) + 1 n if node is the right child of parent(node), 9 rank(node) = 2 rank(parent(node)) + 2 © 2014 Goodrich, Tamassia, Goldwasser Trees 2 B D 4 5 6 C F J 10 G H 15

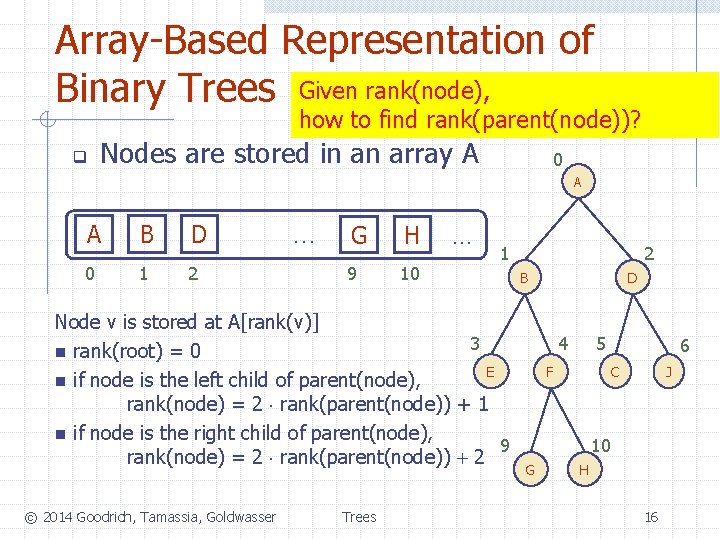
Array-Based Representation of Binary Trees Given rank(node), how to find rank(parent(node))? q Nodes are stored in an array A 0 A A B D 0 1 2 … G H 9 10 … 1 Node v is stored at A[rank(v)] 3 n rank(root) = 0 E n if node is the left child of parent(node), rank(node) = 2 rank(parent(node)) + 1 n if node is the right child of parent(node), 9 rank(node) = 2 rank(parent(node)) + 2 © 2014 Goodrich, Tamassia, Goldwasser Trees 2 B D 4 5 6 C F J 10 G H 16

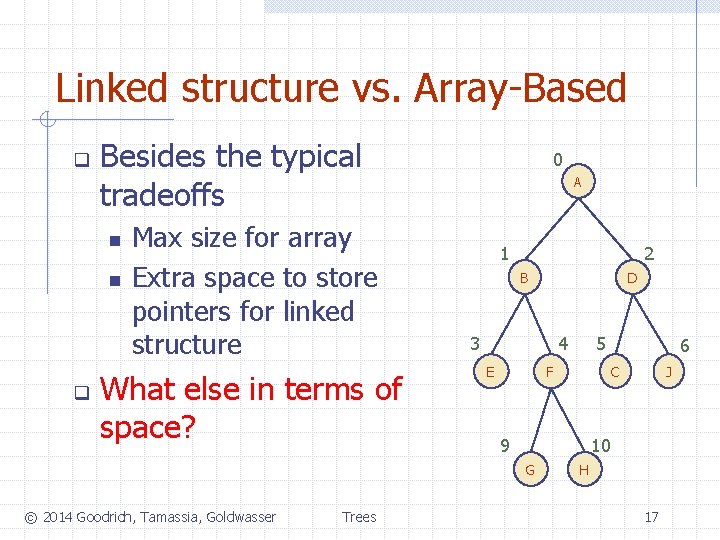
Linked structure vs. Array-Based q Besides the typical tradeoffs n n q Max size for array Extra space to store pointers for linked structure What else in terms of space? 0 A 1 2 B 3 4 E Trees 5 6 C F 9 J 10 G © 2014 Goodrich, Tamassia, Goldwasser D H 17

Time Complexity Operation Linked Structure Array-based left. Child(node) [or right. Child(node)] Parent(node) © 2014 Goodrich, Tamassia, Goldwasser Trees 18

Time Complexity Operation Linked Structure Array-based left. Child(node) [or right. Child(node)] O(1) Parent(node) O(1) © 2014 Goodrich, Tamassia, Goldwasser Trees 19

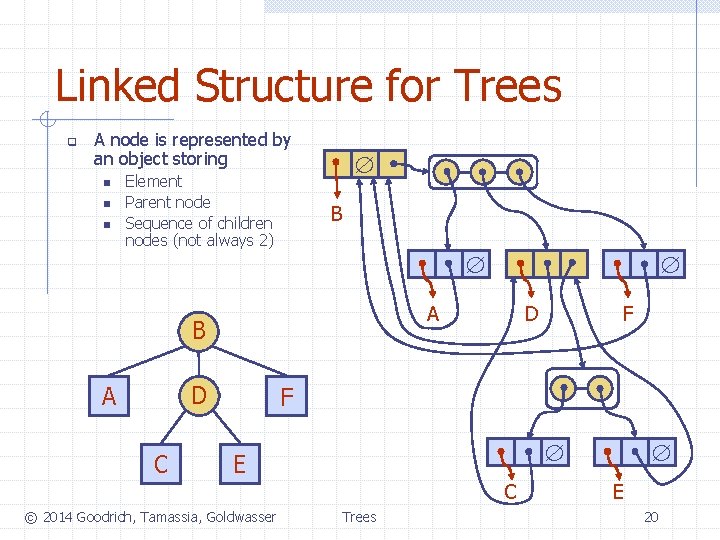
Linked Structure for Trees q A node is represented by an object storing n n n Element Parent node Sequence of children nodes (not always 2) B A B D A C D F F E C © 2014 Goodrich, Tamassia, Goldwasser Trees E 20

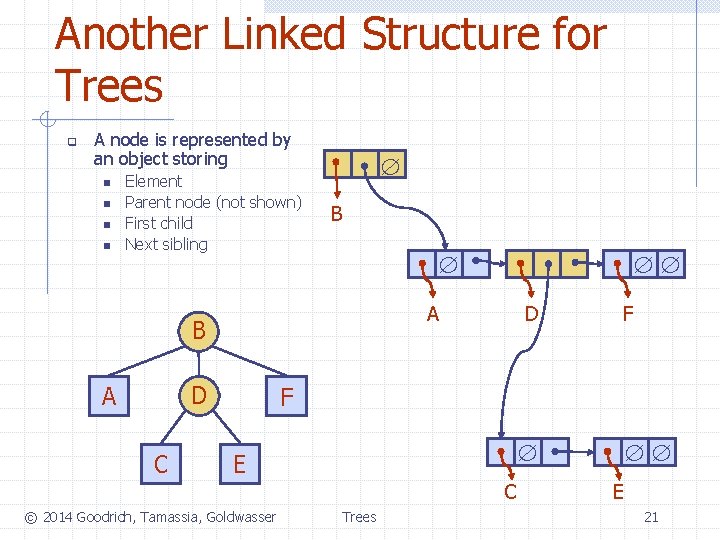
Another Linked Structure for Trees q A node is represented by an object storing n n Element Parent node (not shown) First child Next sibling B A B D A C D F F E C © 2014 Goodrich, Tamassia, Goldwasser Trees E 21

Traversing a Tree q Systematically visiting all tree nodes n n n Help find a particular node Help print the tree … © 2014 Goodrich, Tamassia, Goldwasser Trees 22

Traversal q Systemically visit each element in the data structure n Arrays w increment index n Linked lists w follow “next” pointer n Tree w What would you do? n In O(n) time © 2014 Goodrich, Tamassia, Goldwasser Trees 23

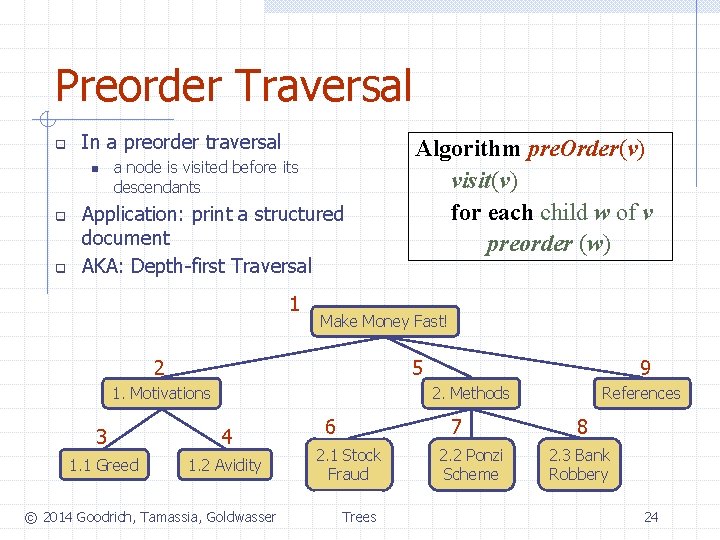
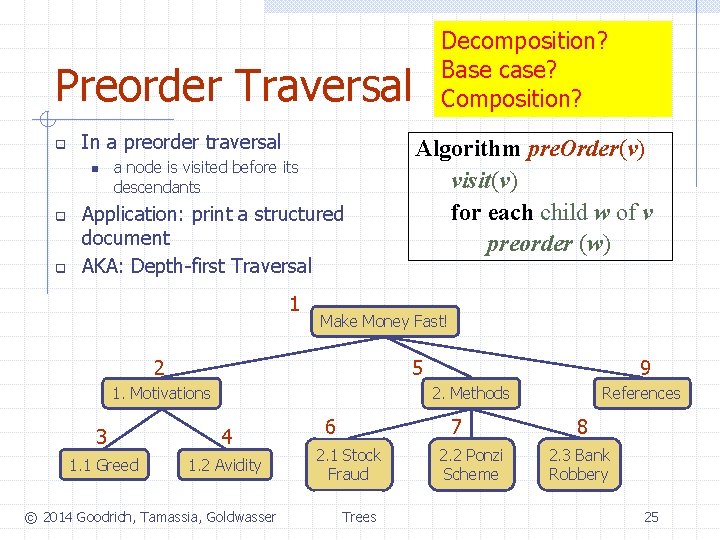
Preorder Traversal q In a preorder traversal n q q a node is visited before its descendants Application: print a structured document AKA: Depth-first Traversal 1 Algorithm pre. Order(v) visit(v) for each child w of v preorder (w) Make Money Fast! 2 5 1. Motivations 9 2. Methods 3 4 1. 1 Greed 1. 2 Avidity © 2014 Goodrich, Tamassia, Goldwasser 6 7 2. 1 Stock Fraud Trees 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery 24

Decomposition? Base case? Composition? Preorder Traversal q In a preorder traversal n q q a node is visited before its descendants Application: print a structured document AKA: Depth-first Traversal 1 Algorithm pre. Order(v) visit(v) for each child w of v preorder (w) Make Money Fast! 2 5 1. Motivations 9 2. Methods 3 4 1. 1 Greed 1. 2 Avidity © 2014 Goodrich, Tamassia, Goldwasser 6 7 2. 1 Stock Fraud Trees 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery 25

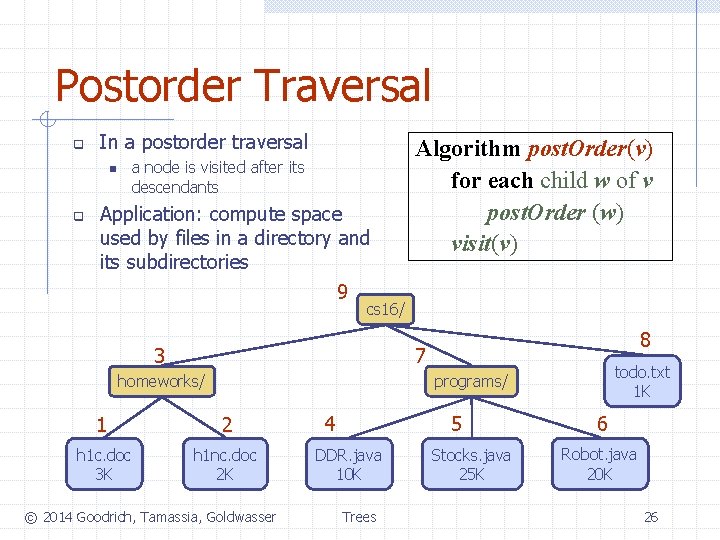
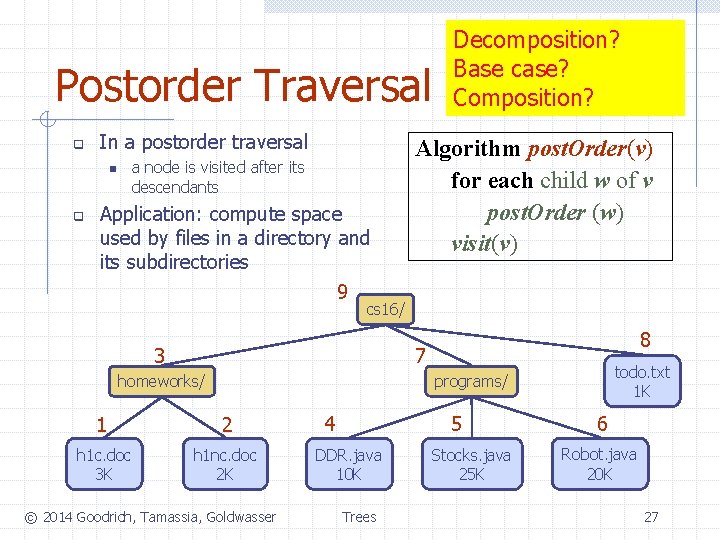
Postorder Traversal q In a postorder traversal a node is visited after its descendants n q Application: compute space used by files in a directory and its subdirectories 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 8 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K © 2014 Goodrich, Tamassia, Goldwasser 4 5 DDR. java 10 K Trees Stocks. java 25 K 6 Robot. java 20 K 26

Postorder Traversal q In a postorder traversal a node is visited after its descendants n q Application: compute space used by files in a directory and its subdirectories 9 Decomposition? Base case? Composition? Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 8 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K © 2014 Goodrich, Tamassia, Goldwasser 4 5 DDR. java 10 K Trees Stocks. java 25 K 6 Robot. java 20 K 27

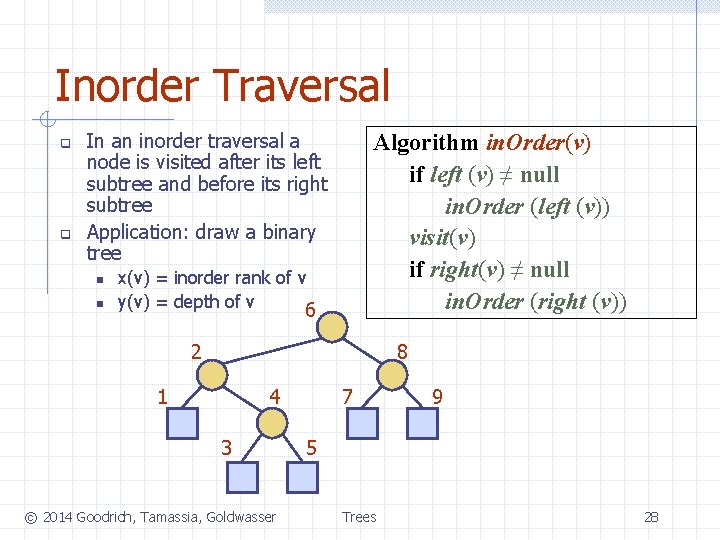
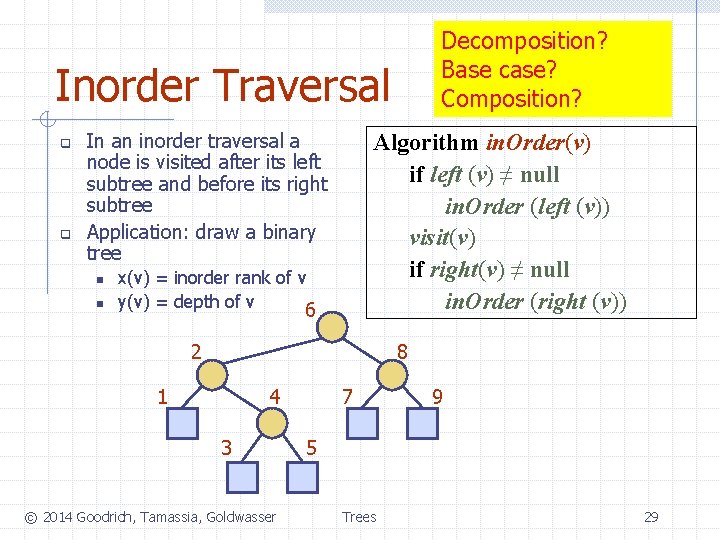
Inorder Traversal q q In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree n n Algorithm in. Order(v) if left (v) ≠ null in. Order (left (v)) visit(v) if right(v) ≠ null in. Order (right (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 © 2014 Goodrich, Tamassia, Goldwasser 7 9 5 Trees 28

Decomposition? Base case? Composition? Inorder Traversal q q In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree n n Algorithm in. Order(v) if left (v) ≠ null in. Order (left (v)) visit(v) if right(v) ≠ null in. Order (right (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 © 2014 Goodrich, Tamassia, Goldwasser 7 9 5 Trees 29

Print Arithmetic Expressions q Specialization of an inorder traversal n n n print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 3 Algorithm print. Expression(v) if left (v) ≠ null print(“(’’) in. Order (left(v)) print(v. element ()) if right(v) ≠ null in. Order (right(v)) print (“)’’) b ((2 (a - 1)) + (3 b)) 1 © 2014 Goodrich, Tamassia, Goldwasser Trees 30

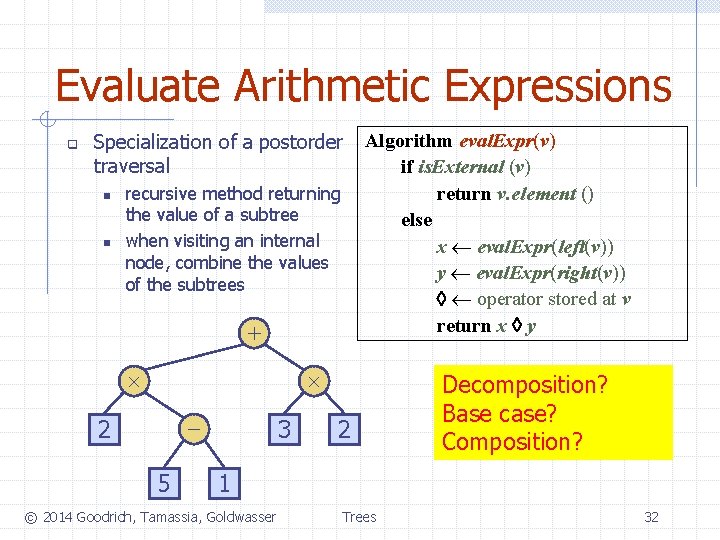
Evaluate Arithmetic Expressions q Specialization of a postorder traversal n n recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees + Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left(v)) y eval. Expr(right(v)) operator stored at v return x y - 2 5 3 2 1 © 2014 Goodrich, Tamassia, Goldwasser Trees 31

Evaluate Arithmetic Expressions q Specialization of a postorder traversal n n recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees + Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left(v)) y eval. Expr(right(v)) operator stored at v return x y - 2 5 3 2 Decomposition? Base case? Composition? 1 © 2014 Goodrich, Tamassia, Goldwasser Trees 32

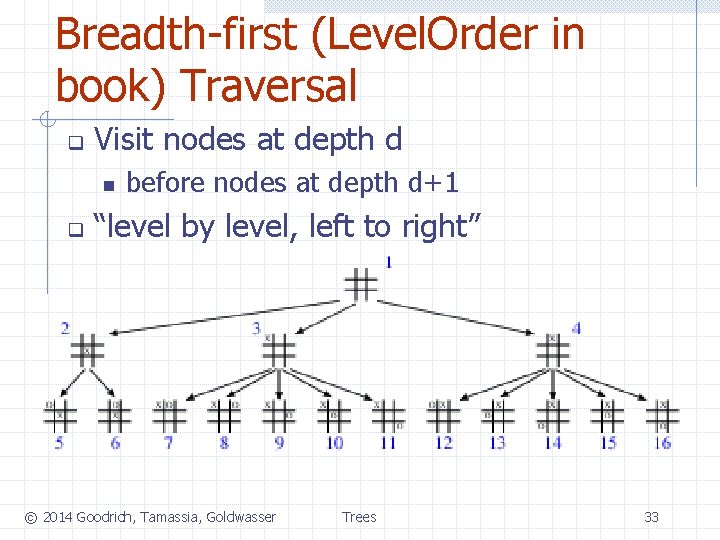
Breadth-first (Level. Order in book) Traversal q Visit nodes at depth d n q before nodes at depth d+1 “level by level, left to right” © 2014 Goodrich, Tamassia, Goldwasser Trees 33

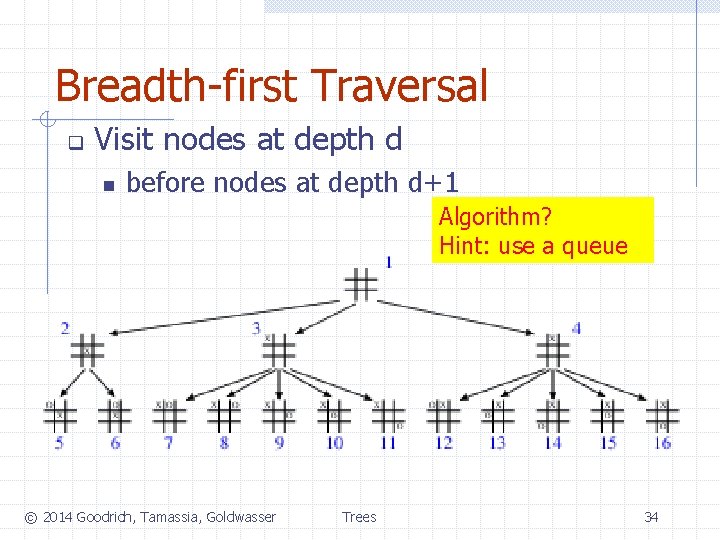
Breadth-first Traversal q Visit nodes at depth d n before nodes at depth d+1 Algorithm? Hint: use a queue © 2014 Goodrich, Tamassia, Goldwasser Trees 34

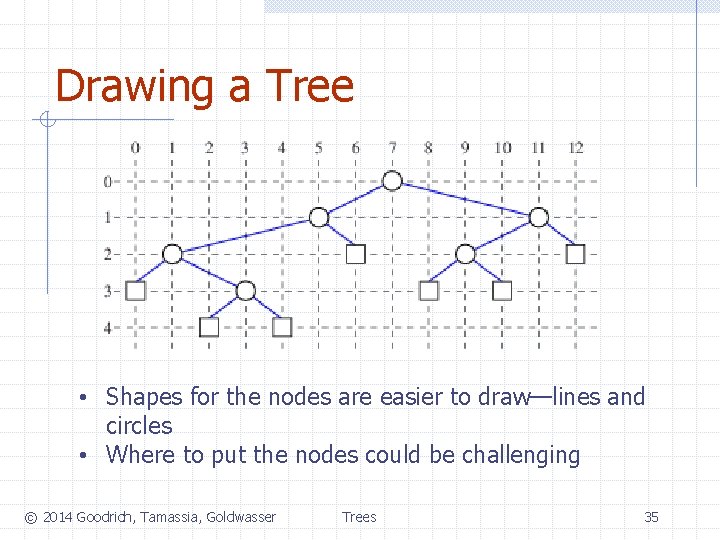
Drawing a Tree • Shapes for the nodes are easier to draw—lines and circles • Where to put the nodes could be challenging © 2014 Goodrich, Tamassia, Goldwasser Trees 35

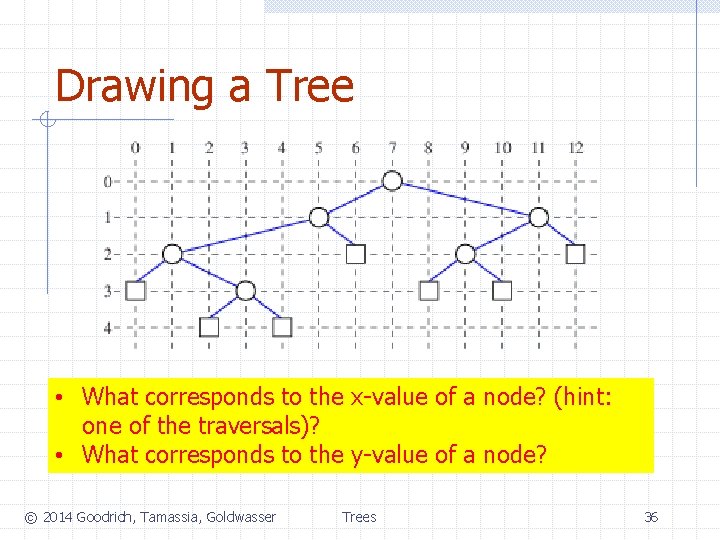
Drawing a Tree • What corresponds to the x-value of a node? (hint: one of the traversals)? • What corresponds to the y-value of a node? © 2014 Goodrich, Tamassia, Goldwasser Trees 36

Depth of Every Node q Print each node and its depth q Use in-order traversal n q Because we need in-order traversal later Algorithm in pseudocode? © 2014 Goodrich, Tamassia, Goldwasser Trees 37

Depth of Every Node d = depth of node 1. print. Depth(node, d) 2. if left. Child 3. print. Depth(left. Child, d+1) 4. print node, d 5. if right. Child 6. print. Depth(right. Child, d+1) q print. Depth(root, 0) © 2014 Goodrich, Tamassia, Goldwasser Trees 38

In-order Traversal Rank q Print each node and its in-order traversal rank © 2014 Goodrich, Tamassia, Goldwasser Trees 39

In-order Traversal Rank x = in-order traversal rank Parameter x: first available (smallest) rank for this tree Return value: next available (largest “+1”) rank after this tree 1. in. Order. Rank(node, x) 2. if left. Child 3. x = in. Order. Rank(left. Child, x) 4. print node, x 5. x++ 6. if right. Child 7. x = in. Order. Rank(right. Child, x) 8. return x © 2014 Goodrich, Tamassia, Goldwasser q in. Order. Rank(root, 0) Trees 40

Drawing a Tree q For each node, instead of printing n n q depth (d) and in-order traversal rank (x) Draw each node at coordinates n n n X-value = x Y-value = d Ie. at (x, d) © 2014 Goodrich, Tamassia, Goldwasser Trees 41

Drawing a Tree x = in-order traversal rank (x value) d = depth of node (y value) 1. draw. Tree(node, d, x) 2. if left. Child 3. x = draw. Tree(left. Child, d+1, x) 4. draw node at (x, d) 5. x++ 6. if right. Child 7. x = draw. Tree(right. Child, d+1, x) 8. return x q draw. Tree(root, 0, 0) © 2014 Goodrich, Tamassia, Goldwasser Trees 42

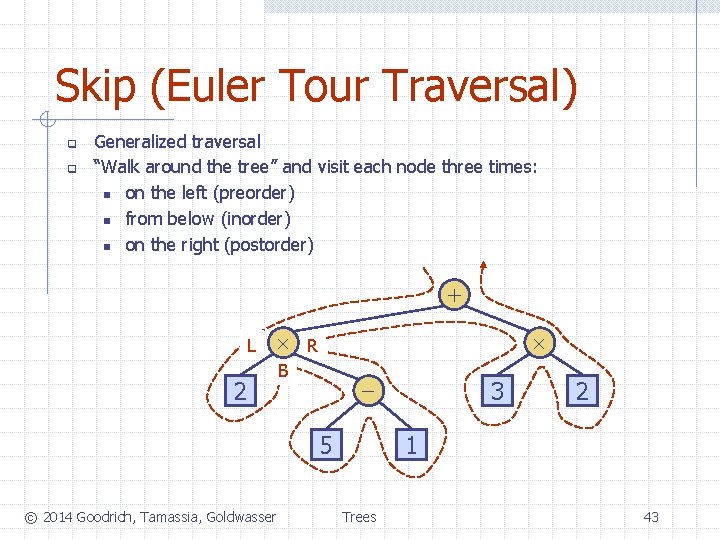
Skip (Euler Tour Traversal) q q Generalized traversal “Walk around the tree” and visit each node three times: n on the left (preorder) n from below (inorder) n on the right (postorder) + L 2 R B 5 © 2014 Goodrich, Tamassia, Goldwasser 3 2 1 Trees 43