TREES Linked Lists vs Trees z With large

TREES

Linked Lists vs Trees z. With large amounts of data, access time for linked lists is quite long. z. Access time can be improved with trees - Linked List : O (n) - Binary Tree : O (square root of n) - Binary Search Tree : O (log n)

Definition z. The Tree Data Structure Õstores objects (nodes) hierarchically Õnodes have parent-child relationships Õoperations include accessing the parent or children of a given node z. A tree T is a set of nodes such that Õthere is a distinguished node r (called the root) of T that has no parent Õeach node v of T except r has a parent node

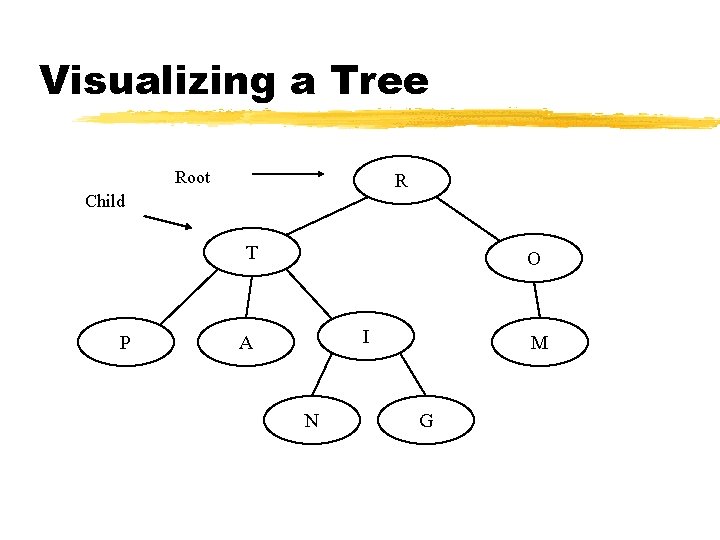
Visualizing a Tree Root R Child T P O I A N M G

Sample Uses z. A company’s organizational structure z. Family tree z. The Java class hierarchy z. O/S directory structure z. Book (parts, chapters, sections) z. Arithmetic expressions z. Web page links (? )

Tree Terminology z. Root Õthe only node that has no parent z. Leaf (External node) Õnode that has no children z. Internal node Õnode that has at least one child z. Siblings Õnodes that have a common parent

More Tree Terminology z. Ancestor Õrecursive definition: ancestors of a node v are v itself and the ancestors of its parent Õproper ancestors: ancestors excluding itself z. Descendant Õv is a descendant of u is an ancestor of v z. Subtree of T rooted at v Õset of all descendants of v

Even More Terminology z. Ordered Tree Õchildren of a node have a strict linear order z. Binary Tree Õan ordered tree where nodes have at most two children (left and right) z. Depth and Height of a node Õdepth: distance from node to root Õheight: from node to its farthest descendant

Tree ADT z. Tree-specific operations Õretrieval: root(), parent(v), children(v) Õtest: is. Internal(v), is. External(v), is. Root(v) z. Container-specific operations ÕTree ADT is just a special type of container Õmethods: size(), is. Empty(), replace(v, e), etc.

Tree Operations z root() z parent(v) z Return the root of T; error if tree is empty Input: None Output: Position (Node) z Return the parent of v; error if v = root() Input: Position Output: Position

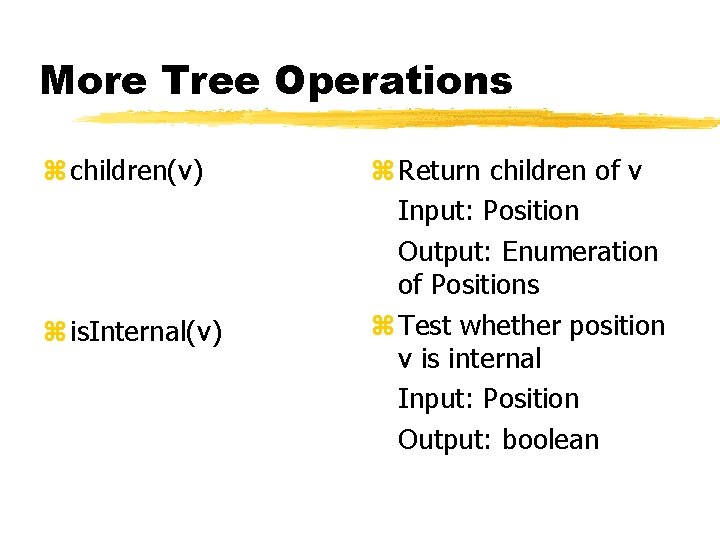
More Tree Operations z children(v) z is. Internal(v) z Return children of v Input: Position Output: Enumeration of Positions z Test whether position v is internal Input: Position Output: boolean

More Tree Operations z is. External(v) z is. Root(v) z Test whether position v is external Input: Position Output: boolean z Test whether position v is the root Input: Position Output: boolean

Container-Specific Operations zsize(): returns number of nodes/positions zis. Empty(): test for empty tree zpositions(): returns all positions zelements(): returns all objects/elements zswap(v, w): swaps elements of 2 positions zreplace(v, e): assigns element to position

Tree Implementation z. Sequence/Array-based implementation Õelements (or references to them) are stored in an array Õparent-child relationships derived from indices z. Linked implementation Õelements stored in nodes Õnodes contain pointers to parent and children

Algorithms on Trees z. Depth computation z. Height computation Õnode height Õtree height z. Traversals Õpreorder Õpostorder

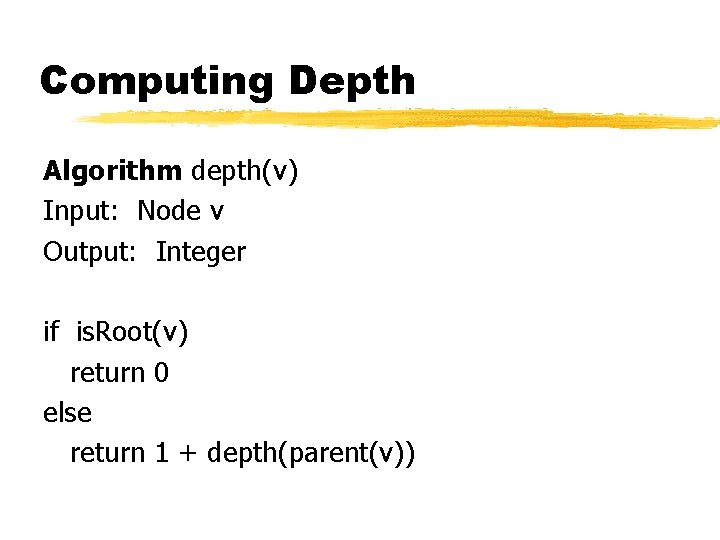
Computing Depth Algorithm depth(v) Input: Node v Output: Integer if is. Root(v) return 0 else return 1 + depth(parent(v))

Computing Node Height Algorithm height(v) Input: Node v Output: Integer if is. External(v) // leaf nodes have 0 height return 0 else m max[height(w)] where w is a child of v return 1 + m

Computing Tree Height z. Method 1 Õcompute the depths of all the leaves Õget the maximum z. Method 2 Õcompute height of root recursively Õheight of a node is one plus the maximum height of the subtrees rooted at its children Õheights of subtrees rooted at leaves: 0

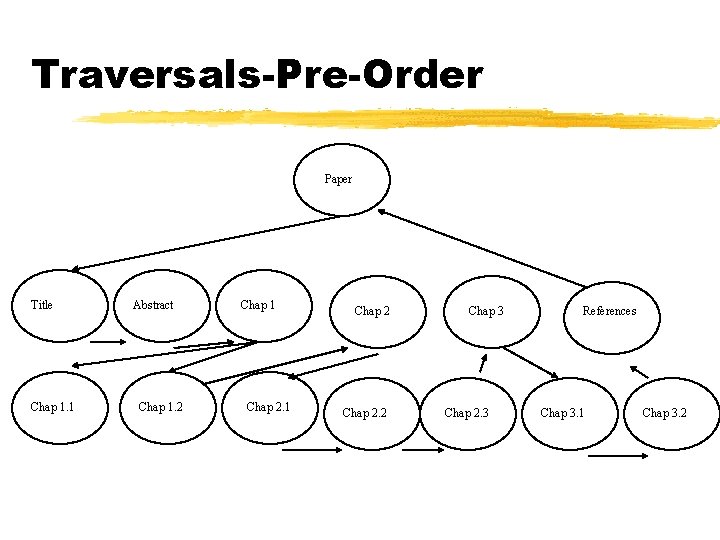
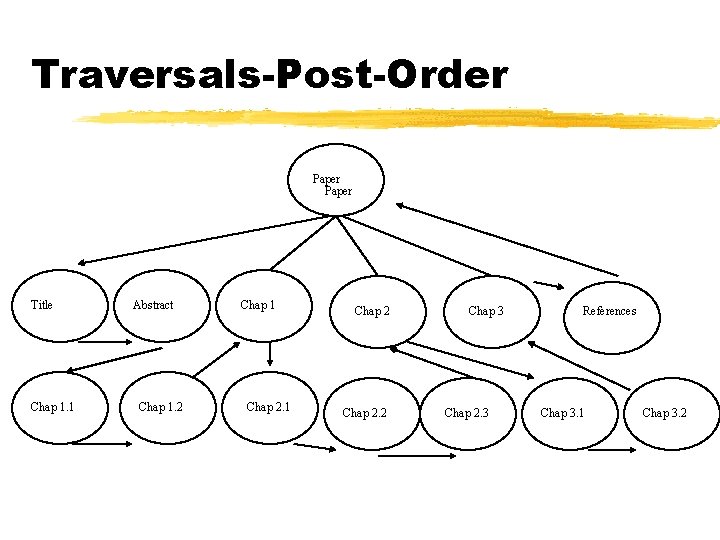
Traversals z. Traversal Õsystematic way of accessing or visiting the nodes of a tree z. Preorder Õvisit root first, then traverse its subtrees (recursive) z. Postorder Õvisit subtrees first, then root (recursive)

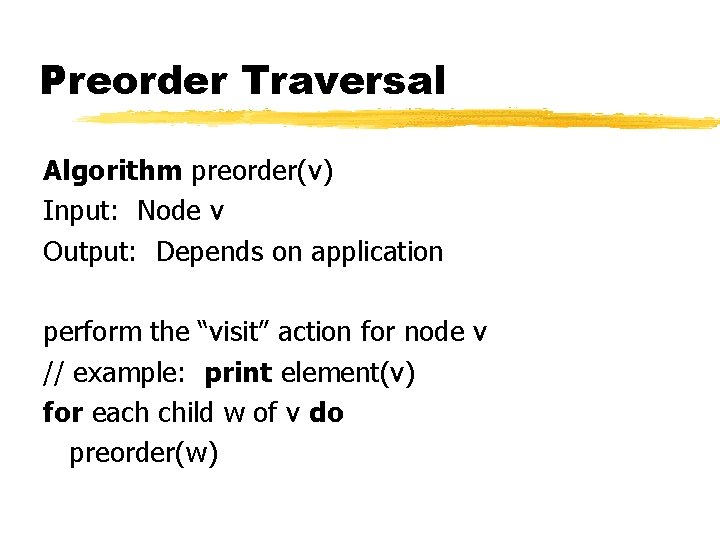
Preorder Traversal Algorithm preorder(v) Input: Node v Output: Depends on application perform the “visit” action for node v // example: print element(v) for each child w of v do preorder(w)

Postorder Traversal Algorithm postorder(v) Input: Node v Output: Depends on application for each child w of v do postorder(w) perform the “visit” action for node v // example: print element(v)

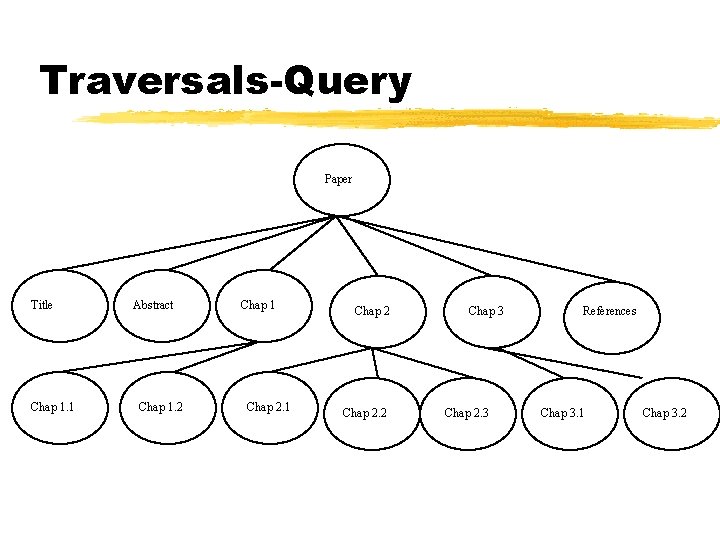
Traversals - Query z. Given the following tree, show (by arrows) a preorder and a post-order traversal.

Traversals-Query Paper Title Chap 1. 1 Abstract Chap 1. 2 Chap 1 Chap 2. 2 Chap 3 Chap 2. 3 References Chap 3. 1 Chap 3. 2

Traversals-Pre-Order Paper Title Chap 1. 1 Abstract Chap 1. 2 Chap 1 Chap 2. 2 Chap 3 Chap 2. 3 References Chap 3. 1 Chap 3. 2

Traversals-Post-Order Paper Title Chap 1. 1 Abstract Chap 1. 2 Chap 1 Chap 2. 2 Chap 3 Chap 2. 3 References Chap 3. 1 Chap 3. 2

Binary Trees z. Definition - A binary tree is a tree in which no nodes can have more than two children z- average depth is O (square root of n) z- special tree, binary search tree has an average depth of O (log n)

Binary Tree Properties Given a binary tree with n nodes, i internal nodes, e external nodes and height h: Õ h+1 <= e <= 2 h Õ h <= i <= 2 h -1 Õ 2 h +1 <= n <= 2 h+1 -1 Õ log(n+1) -1 <= h <= (n-1)/2 (Minimum height is O(log n))

Binary Tree access methods z left. Child(v) z right. Child(v) z Return the left child of v; error if external Input: Position Output: Position z Return the right child of v; error if external Input: Position Output: Position

Binary Tree insertion update methods z expand. External(v) z Create two nodes under node v; error if internal z remove. Above. External(v) z Remove parent of v including its two children; error if internal

Binary Trees- Query z. What tree is produced by a pre-order traversal of a binary tree ?

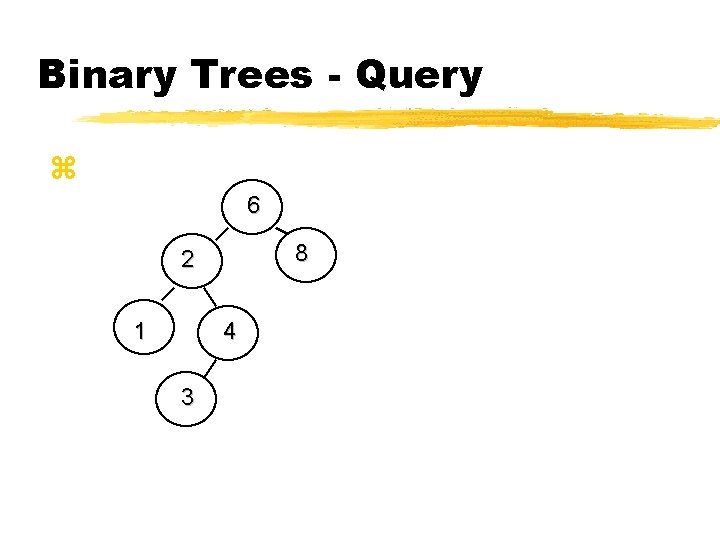
Binary Trees - Query z 6 8 2 1 4 3

Binary Tree Uses z. Heaps / Priority queues z. Arithmetic expression trees z. Decision trees z. Binary-search trees ÕDatabase storage (B+ Trees)

Binary Tree Traversals z. Preorder and Postorder ÕSame as general case ÕWhen processing children of a node, left child first, right child next z. Inorder Traversal Õapplies to binary trees only Õrecursively process left subtree, then root, then right subtree

Inorder Traversal for Binary Trees Algorithm inorder(v) Input: Node v Output: Depends on application if is. Internal(v) then inorder(left. Child(v)) perform the “visit” action for node v // example: print element(v) if is. Internal(v) then inorder(right. Child(v))

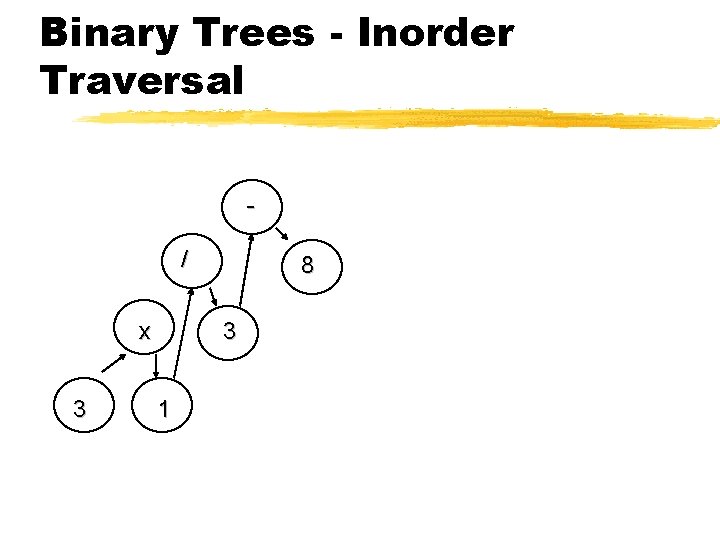
Binary Trees - Inorder Traversal / x 3 8 3 1

Binary Trees - Expression z. Expressions can be represented by a binary tree z. The leaves of an expression tree are operands (i. e. constants, variables, etc) z. Other nodes are the operators

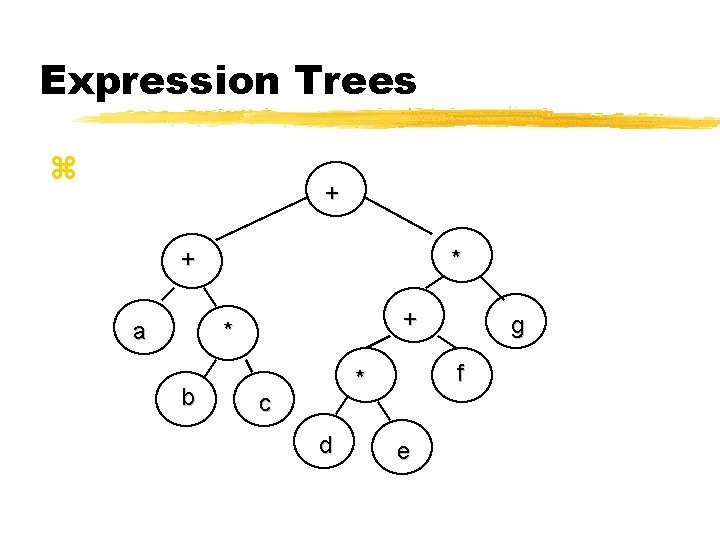
Expression Trees z. Example The expression (a+b*c)+((d*e+f)*g) can be represented as follows :

Expression Trees z + + a * + * b f * c d g e

Expression Trees z. If you do a post-traversal of the tree, the result is as follows : abc*+def+g*+ z. Postfix notation of the expression z. Compiler design

Expression Trees - Query z. Make an expression tree of the following formula : (a*b) * (c+d) - e

Binary Tree Array-Based Implementation z. Use array S[1. . max] to store elements Õderive parent/child relationships from indices z. Let i be an array index, S[i] be the node Õi = 1 for the root node Õleft child of S[i] is S[2*i] Õright child of S[i] is S[2*i+1] Õparent of S[i] is S[i/2] z. Slightly different formula if S[0. . max-1]

BT Array Implementation continued z. Implementations of root(), parent(v), left. Child(v), right. Child() and test methods Õsimple arithmetic computations z. May need an integer n to represent last valid node/first available node in the array Õe. g. , when implementing a heap z. Disadvantages: Õmaximum size has to be predetermined Õspace-inefficient for “skewed” trees

Binary Tree Linked Implementation z. Need a Node class containing Õelement Õleft, right and parent of class Node Õusual set/get methods z. Binary Tree class now contains Õroot variable of class Node Õsize variable (int) to monitor tree size

BT Linked Implementation continued z. Access and test methods Õall involve inspecting node data zexpand. External(v) Õcreate two nodes and set some pointers zremove. Above. External(v) Õreset child pointer of grandparent to null Õdispose garbage nodes (automatic in Java)

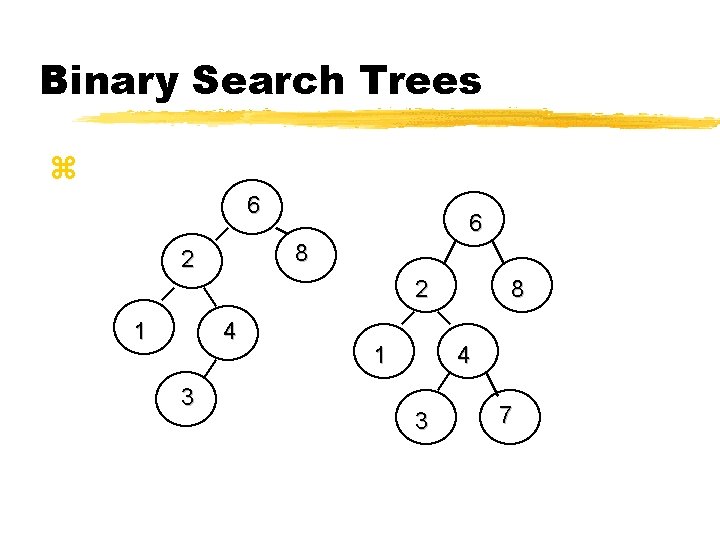
Binary Search Trees z. For every node x, in the tree, the values of all the keys in the left subtree are smaller than the key value in x and the values of all the keys in the right subtree are larger than the key value in x z. Average depth (access time) is O (log(n))

Binary Search Trees z 6 6 8 2 26 1 4 3 1 8 4 3 7

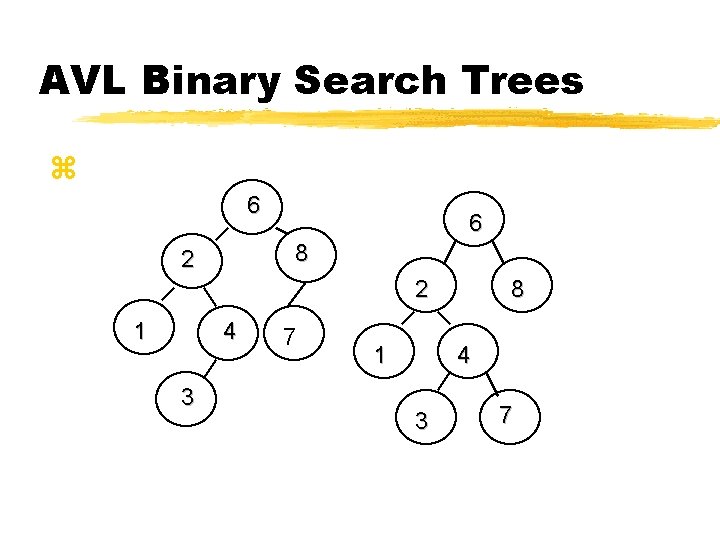
Binary Search Tree - AVL z. Definition - It is a binary search tree with a balance condition - for every node in the tree, the average height of the left and right subtrees can differ by at most one (1).

AVL Binary Search Trees z 6 6 8 2 26 1 4 3 7 1 8 4 3 7

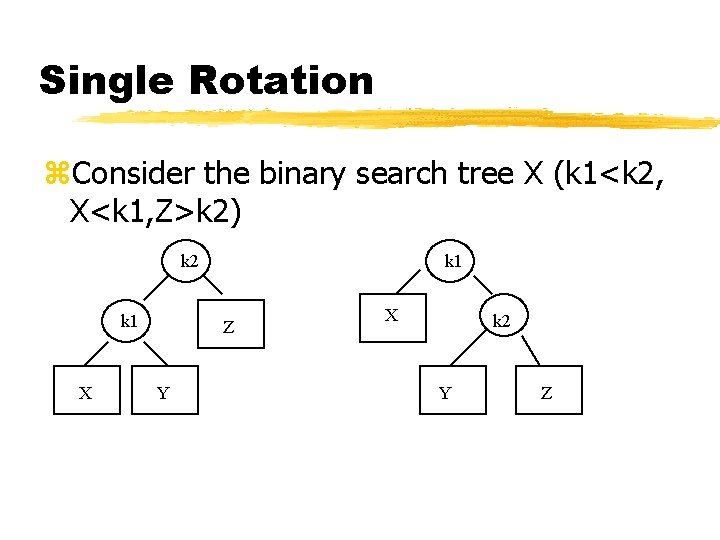
AVL Binary Search Trees z. Binary Search Trees are transformed to AVL Binary Search Trees by a process called rotation

Single Rotation z. Consider the binary search tree X (k 1<k 2, X<k 1, Z>k 2) k 2 k 1 X k 1 Z Y X Z Z k 2 Y Z

AVL Binary Search Trees z. Problem : Construct a AVL Binary Search Tree of the keys 1 - 7 assuming that the keys will be in sequential order.

z THE END