Trees general rooted binary balanced In graph theory

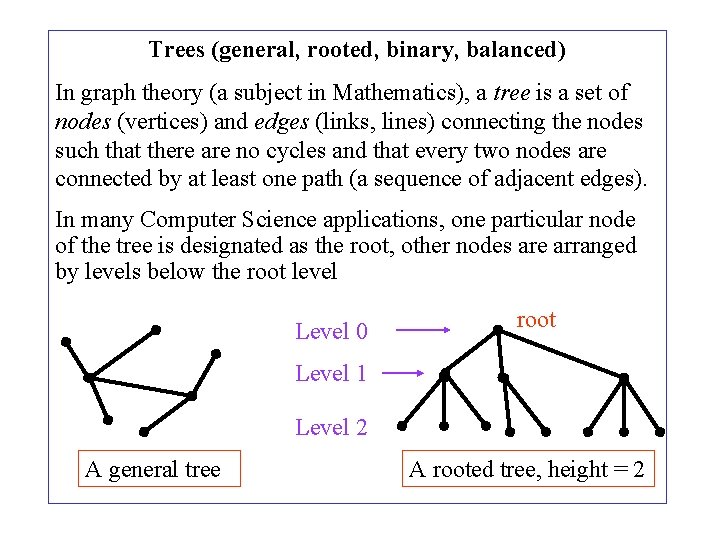
Trees (general, rooted, binary, balanced) In graph theory (a subject in Mathematics), a tree is a set of nodes (vertices) and edges (links, lines) connecting the nodes such that there are no cycles and that every two nodes are connected by at least one path (a sequence of adjacent edges). In many Computer Science applications, one particular node of the tree is designated as the root, other nodes are arranged by levels below the root level Level 0 root Level 1 Level 2 A general tree A rooted tree, height = 2

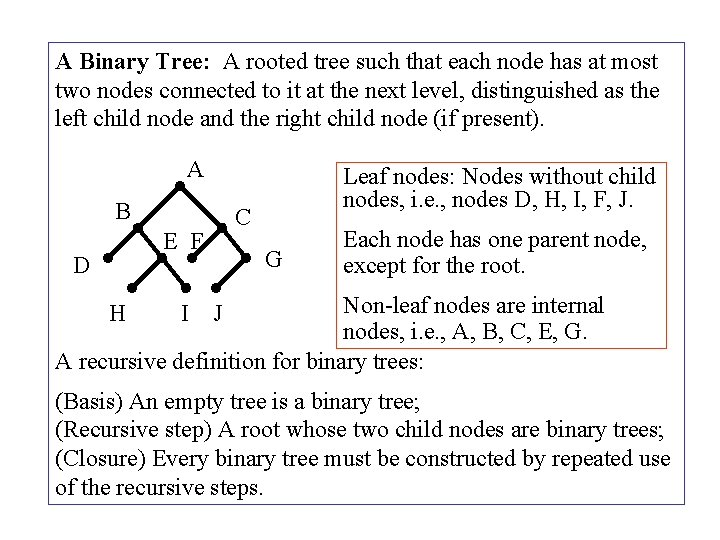
A Binary Tree: A rooted tree such that each node has at most two nodes connected to it at the next level, distinguished as the left child node and the right child node (if present). A B C E F D Leaf nodes: Nodes without child nodes, i. e. , nodes D, H, I, F, J. G Each node has one parent node, except for the root. Non-leaf nodes are internal nodes, i. e. , A, B, C, E, G. A recursive definition for binary trees: H I J (Basis) An empty tree is a binary tree; (Recursive step) A root whose two child nodes are binary trees; (Closure) Every binary tree must be constructed by repeated use of the recursive steps.

A Binary. Node class in Java: class Binary. Node { // Constructors Binary. Node(Comparable the. Element ) { this( the. Element, null ); } Binary. Node(Comparable the. Element, Binary. Node lt, Binary. Node rt) { element = the. Element; left = lt; right = rt; } // Friendly data; accessible by other package routines } Comparable element; // The data in the node Binary. Node left; // Left child Binary. Node right; // Right child

Theorem. Suppose T is a binary tree of n nodes, n 1, and height h 0. Let nq denote the total number of nodes at level q, for 0 q h. The following properties hold: (a) nq 2 q, for 0 q h; (b) Proof: We prove (a) by using induction on q, the level number. (Basis Step) When q = 0, that is, at the root level, there is only one node (the root). Thus, n 0 = 1 = 20 2 q. So the Basis Step is proved. (Induction Hypothesis) Consider q = k. Suppose Property (a) holds for level k, that is suppose nk = the total number of nodes of tree T at level k 2 k for some k 0. (Induction Step) Consider q = k + 1. We need to prove nk+1 2 k+1 ------ (1). Since each node at level (k + 1) must be a child of a node at level k, by the definition of level, and since each node has at most two child nodes, by the definition of binary tree, so the total number of nodes at level (k + 1) = nk+1 2 (nk) 2 (2 k) by the Induction Hypothesis = 2 k+1 = RHS of (1). Thus, the Induction Step is proved. By induction, we proved nq 2 q, for 0 q h.

(b) Note that the sum of all the nodes of all levels is equal to n; therefore, Applying the following summation formula (which can be proved using induction) substituting x = 2 and m = h yields which can be substituted into (2) to prove (b). In particular, if a binary tree is full, each level k has all 2 k nodes for 0 k the height h, then n = 2 h+1 – 1, or equivalently, h + 1 = lg(n+1). In general, lg(n+1) – 1 h n – 1. The tree is skewed if h is close to n – 1, . A skewed binary tree, height = n – 1 = 4.

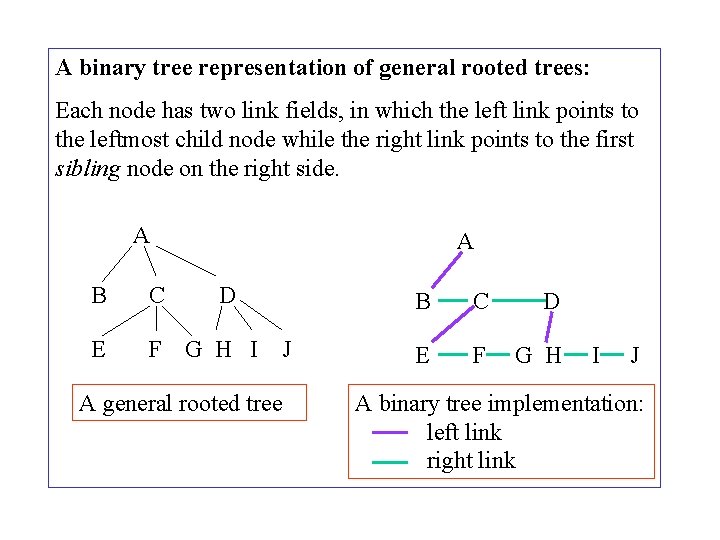
A binary tree representation of general rooted trees: Each node has two link fields, in which the left link points to the leftmost child node while the right link points to the first sibling node on the right side. A A B C D E F G H I J A general rooted tree B C D E F G H I J A binary tree implementation: left link right link

Common Tree Traversal Template public void traverse ( ) { action 0; Tree child = left. Child; if (child == null) return; child. traverse(); action 1; child = child. right. Sibling; if (child == null) return; child. traverse(); action 2; child = child. right. Sibling; … if (child == null) return; child. traverse(); action. K; } // traverse

Binary Expression Trees Labels are operators or atomic operands All operators are interior nodes. Common labels are +, –, *, / and unary – All atomic operands are leaves Inductive Definition A single atomic operand is represented by a single node binary tree If E and F are expressions represented by binary trees S and T, respectively, and op is a binary operator, then (E op F) is represented by the binary tree U consisting a new root labeled op with left child S and right child T. If E is an expression represented by tree S and op is a prefix unary operator, then (op E) is represented by the binary tree T consisting a new root labeled op with empty left child and right child S. Example Uses Interpreters and expression trees Compilers and expression trees Optimizing compilers and expression trees

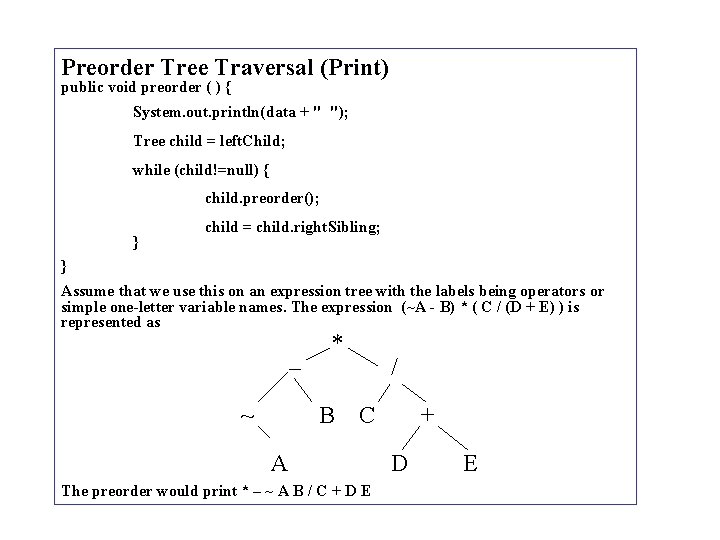
Preorder Tree Traversal (Print) public void preorder ( ) { System. out. println(data + " "); Tree child = left. Child; while (child!=null) { child. preorder(); } child = child. right. Sibling; } Assume that we use this on an expression tree with the labels being operators or simple one-letter variable names. The expression (~A - B) * ( C / (D + E) ) is represented as – ~ * B / C A The preorder would print * – ~ A B / C + D E

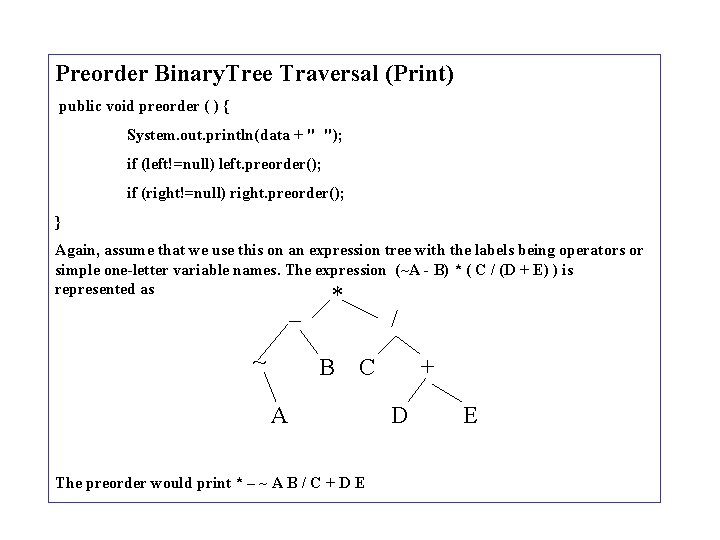
Preorder Binary. Tree Traversal (Print) public void preorder ( ) { System. out. println(data + " "); if (left!=null) left. preorder(); if (right!=null) right. preorder(); } Again, assume that we use this on an expression tree with the labels being operators or simple one-letter variable names. The expression (~A - B) * ( C / (D + E) ) is represented as – ~ * B / C A The preorder would print * – ~ A B / C + D E

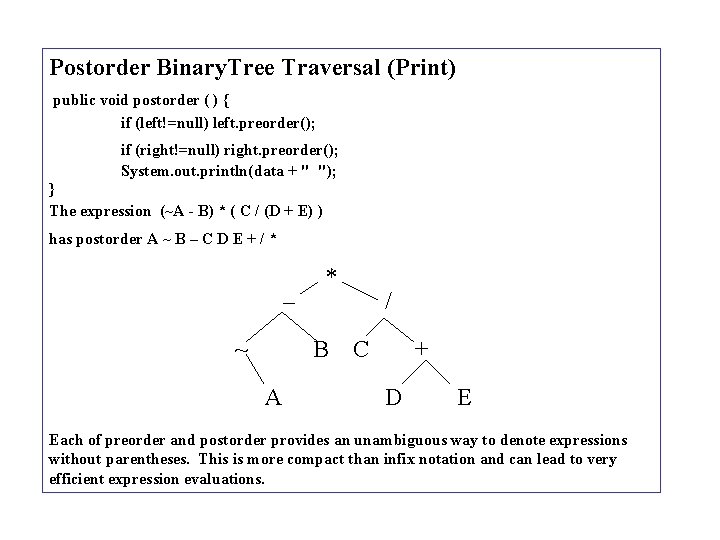
Postorder Binary. Tree Traversal (Print) public void postorder ( ) { if (left!=null) left. preorder(); if (right!=null) right. preorder(); System. out. println(data + " "); } The expression (~A - B) * ( C / (D + E) ) has postorder A ~ B – C D E + / * – ~ * B A / C + D E Each of preorder and postorder provides an unambiguous way to denote expressions without parentheses. This is more compact than infix notation and can lead to very efficient expression evaluations.

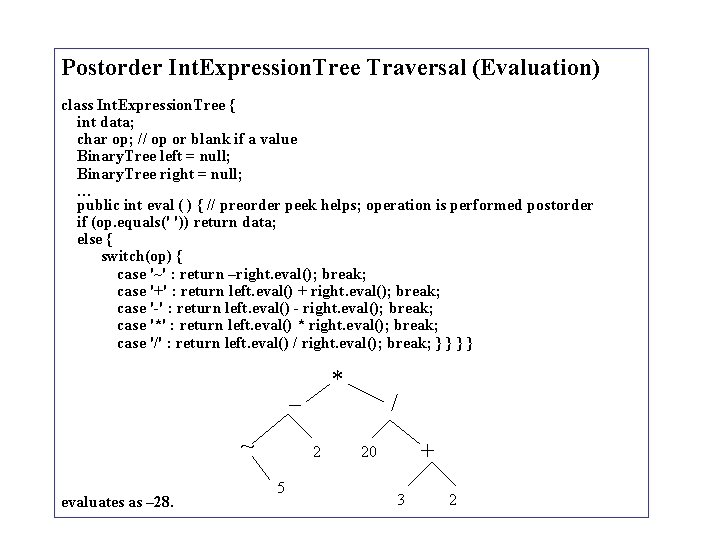
Postorder Int. Expression. Tree Traversal (Evaluation) class Int. Expression. Tree { int data; char op; // op or blank if a value Binary. Tree left = null; Binary. Tree right = null; … public int eval ( ) { // preorder peek helps; operation is performed postorder if (op. equals(' ')) return data; else { switch(op) { case '~' : return –right. eval(); break; case '+' : return left. eval() + right. eval(); break; case '-' : return left. eval() - right. eval(); break; case '*' : return left. eval() * right. eval(); break; case '/' : return left. eval() / right. eval(); break; } } * – ~ evaluates as – 28. 2 5 / + 20 3 2

Inorder and Binary Expression Trees public void inorder ( ) { System. out. println("("); if (left!=null) left. preorder(); System. out. println(data); if (right!=null) right. preorder(); System. out. println(")"); } – ~ B A The expression (~A - B) * ( C / (D + E) ) is printed as (((~(A))–(B))*(((C)/((D)+(E))))) The correct fully parenthesized version. * / C + D E

Binary Search Trees: A binary tree (i. e. a rooted tree in which each node has a left and right children which are also binary trees), such that the object (data) field contains elements which can be compared, resulting in less than, equal, or greater than results. A c++ Binary. Search. Tree node class definition: template <class Comparable> class Binary. Search. Tree; template <class Comparable> class Binary. Node { Comparable element; // class Comparable allows comparisons Binary. Node *left; Binary. Node *right; Binary. Node( const Comparable & the. Element, Binary. Node *lt, Binary. Node *rt ) : element(the. Element), left(lt), right(rt) { } friend class Binary. Search. Tree<Comparable>; };

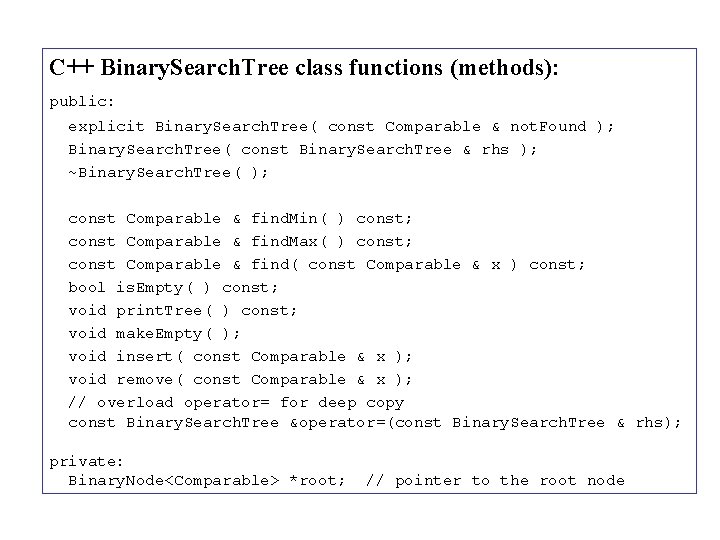
C++ Binary. Search. Tree class functions (methods): public: explicit Binary. Search. Tree( const Comparable & not. Found ); Binary. Search. Tree( const Binary. Search. Tree & rhs ); ~Binary. Search. Tree( ); const Comparable & find. Min( ) const; const Comparable & find. Max( ) const; const Comparable & find( const Comparable & x ) const; bool is. Empty( ) const; void print. Tree( ) const; void make. Empty( ); void insert( const Comparable & x ); void remove( const Comparable & x ); // overload operator= for deep copy const Binary. Search. Tree &operator=(const Binary. Search. Tree & rhs); private: Binary. Node<Comparable> *root; // pointer to the root node

Insert(): an element (of Comparable) to tree: template <class Comparable> void Binary. Search. Tree<Comparable>: : insert(const Comparable & x) { insert(x, root); // call an internal insert from the root }; /** * Internal method to insert item x into a subtree rooted at t; * set the new root t if it is empty */ template <class Comparable> void Binary. Search. Tree<Comparable>: : insert(const Comparable & x, Binary. Node<Comparable> *& t) const { if( t == NULL ) t = new Binary. Node<Comparable>( x, NULL ); else if( x < t->element ) insert( x, t->left ); else if( t->element < x ) insert( x, t->right ); else ; // Duplicate; do nothing }

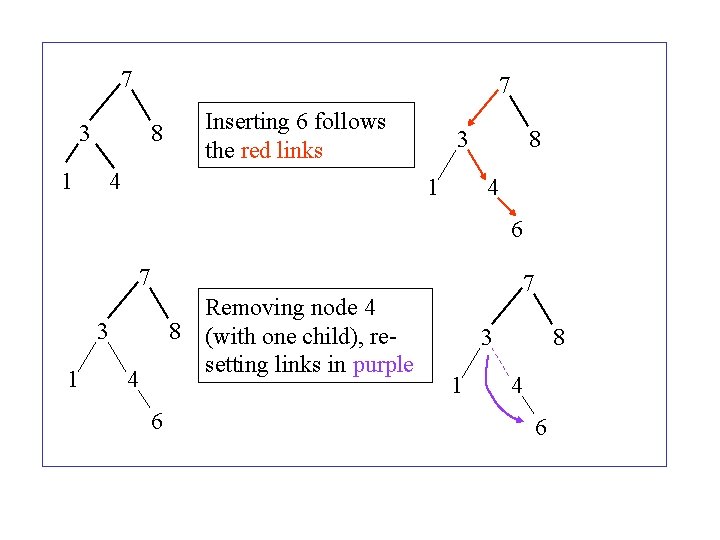
7 7 3 Inserting 6 follows the red links 8 1 4 3 1 8 4 6 7 3 1 8 4 6 Removing node 4 (with one child), resetting links in purple 7 3 1 8 4 6

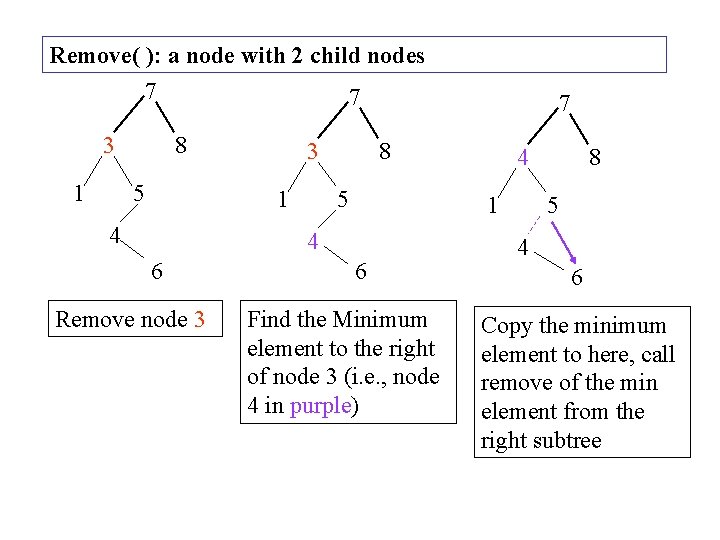
Remove( ): a node with 2 child nodes 7 7 3 1 8 5 3 1 4 8 5 Remove node 3 4 1 4 6 7 6 Find the Minimum element to the right of node 3 (i. e. , node 4 in purple) 8 5 4 6 Copy the minimum element to here, call remove of the min element from the right subtree

C++ code for remove( ): /** * An internal method called from a public method remove(x) to * remove x from a subtree rooted at t; set the new root t if it * is empty */ template <class Comparable> void Binary. Search. Tree<Comparable>: : remove( const Comparable & x, Binary. Node<Comparable>*& t) const { if( t == NULL return; // Item not found; do nothing if( x < t->element ) remove( x, t->left ) else if( t->element < x ) remove( x, t->right ); else if(t->left != NULL && t->right != NULL) // two children { t->element = find. Min( t->right )->element; remove( t->element, t->right ); } else // one child { Binary. Node<Comparable> *old. Node = t; t = ( t->left != NULL ) ? t->left : t->right; delete old. Node; } }

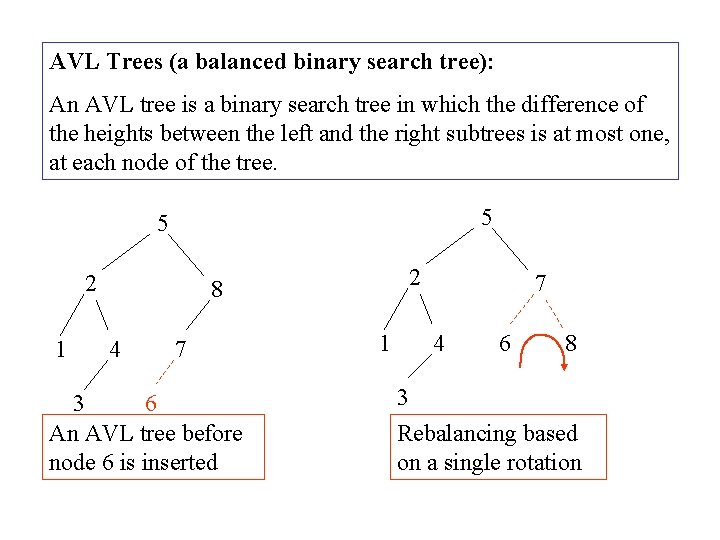
AVL Trees (a balanced binary search tree): An AVL tree is a binary search tree in which the difference of the heights between the left and the right subtrees is at most one, at each node of the tree. 5 5 2 1 2 8 4 7 3 6 An AVL tree before node 6 is inserted 1 7 4 6 8 3 Rebalancing based on a single rotation

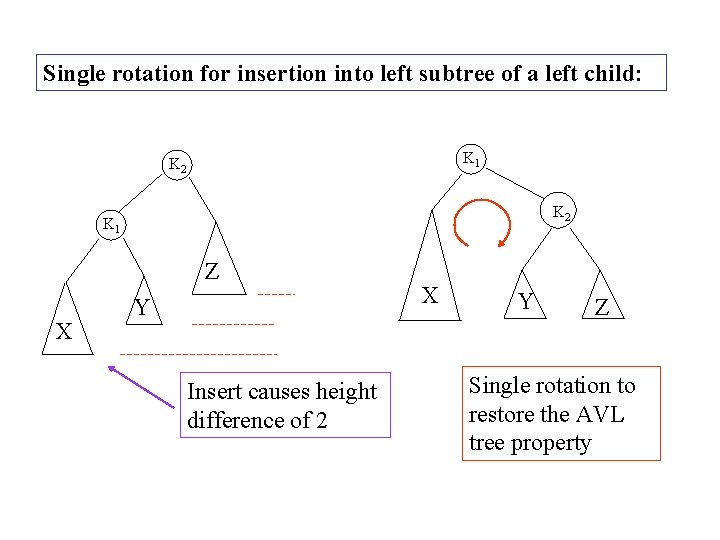
Single rotation for insertion into left subtree of a left child: K 1 K 2 K 1 Z X Y Insert causes height difference of 2 X Y Z Single rotation to restore the AVL tree property

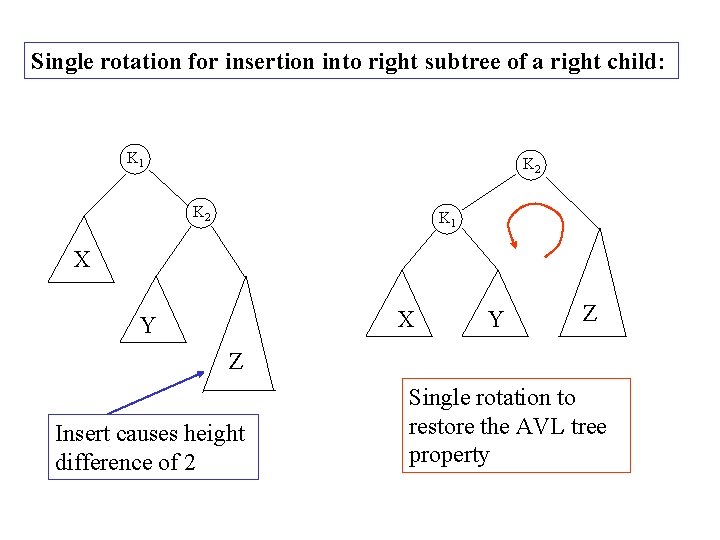
Single rotation for insertion into right subtree of a right child: K 1 K 2 K 1 X X Y Y Z Z Insert causes height difference of 2 Single rotation to restore the AVL tree property

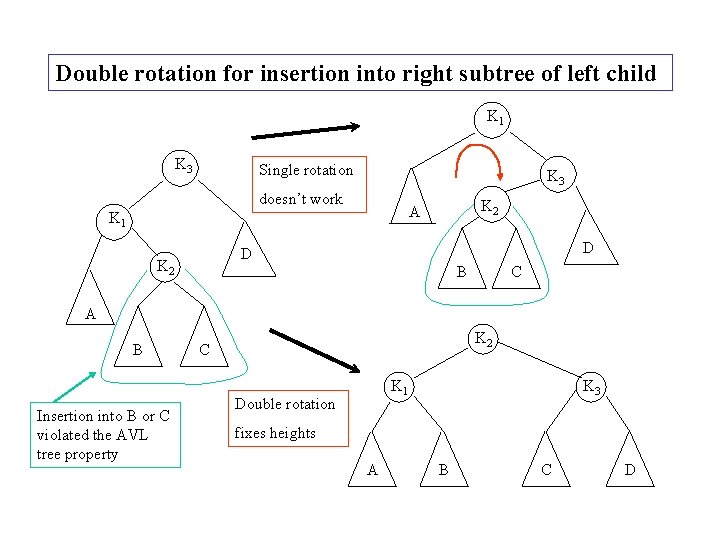
Double rotation for insertion into right subtree of left child K 1 K 3 Single rotation K 3 doesn’t work K 2 A K 1 D D K 2 B C A B Insertion into B or C violated the AVL tree property K 2 C K 1 Double rotation K 3 fixes heights A B C D