Trees Definition of a Tree Tree Terminology Importance

Trees • Definition of a Tree • Tree Terminology • Importance of Trees • Implementation of Trees • Binary Trees • – Definition – Full and Complete Binary Trees – Implementation and Applications Binary Search Trees – Definition – Importance – Implementation – Insertion – Deletion 1

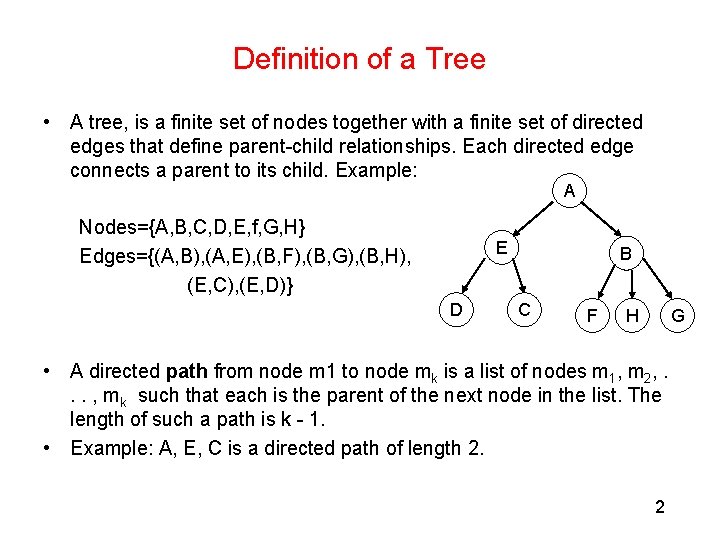
Definition of a Tree • A tree, is a finite set of nodes together with a finite set of directed edges that define parent-child relationships. Each directed edge connects a parent to its child. Example: A Nodes={A, B, C, D, E, f, G, H} Edges={(A, B), (A, E), (B, F), (B, G), (B, H), (E, C), (E, D)} E D B C F H G • A directed path from node m 1 to node mk is a list of nodes m 1, m 2, . . . , mk such that each is the parent of the next node in the list. The length of such a path is k - 1. • Example: A, E, C is a directed path of length 2. 2

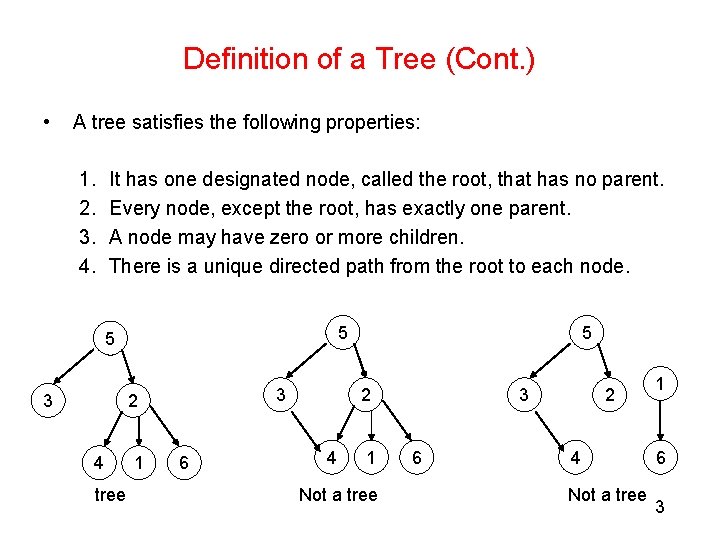
Definition of a Tree (Cont. ) • A tree satisfies the following properties: 1. 2. 3. 4. It has one designated node, called the root, that has no parent. Every node, except the root, has exactly one parent. A node may have zero or more children. There is a unique directed path from the root to each node. 5 5 3 3 2 4 tree 1 6 5 2 4 1 Not a tree 3 6 2 4 Not a tree 1 6 3

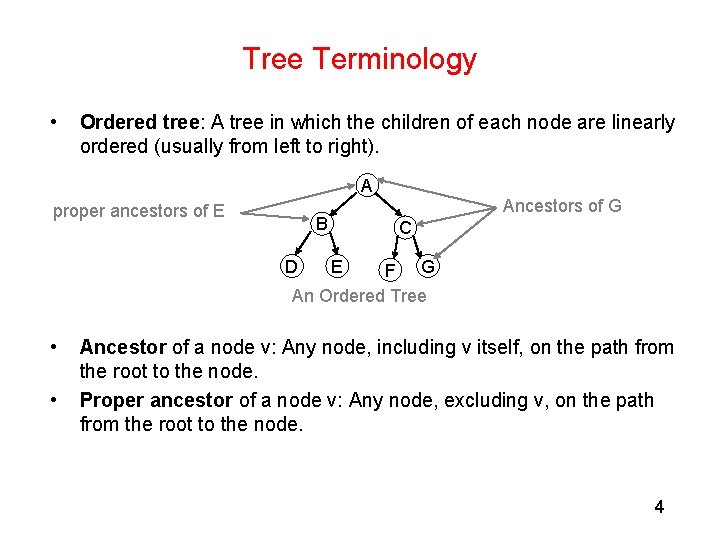
Tree Terminology • Ordered tree: A tree in which the children of each node are linearly ordered (usually from left to right). A proper ancestors of E B Ancestors of G C F G An Ordered Tree D • • E Ancestor of a node v: Any node, including v itself, on the path from the root to the node. Proper ancestor of a node v: Any node, excluding v, on the path from the root to the node. 4

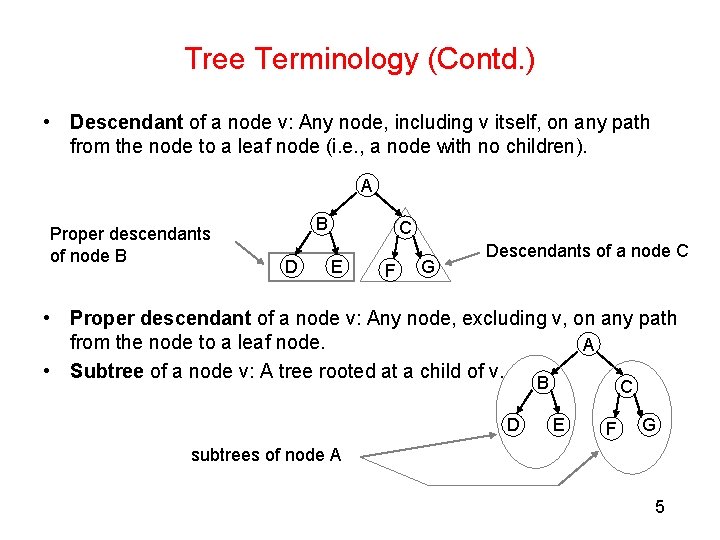
Tree Terminology (Contd. ) • Descendant of a node v: Any node, including v itself, on any path from the node to a leaf node (i. e. , a node with no children). A Proper descendants of node B B D C E F G Descendants of a node C • Proper descendant of a node v: Any node, excluding v, on any path from the node to a leaf node. A • Subtree of a node v: A tree rooted at a child of v. B D C E F G subtrees of node A 5

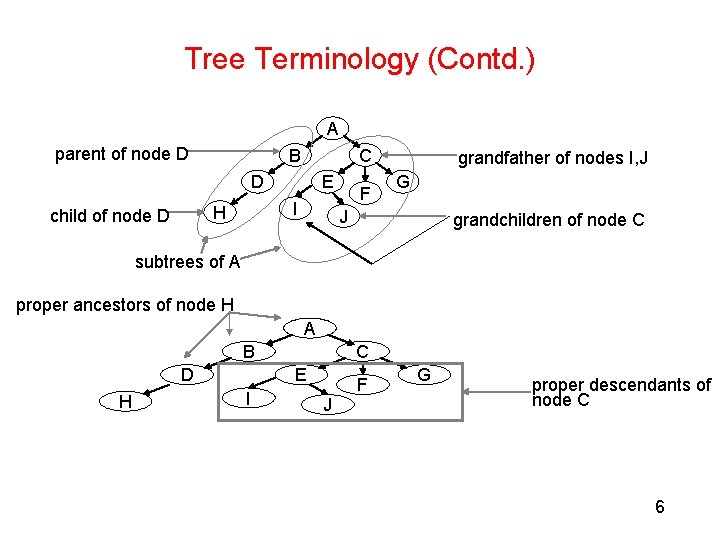
Tree Terminology (Contd. ) A parent of node D B C D I H child of node D E F grandfather of nodes I, J G J grandchildren of node C subtrees of A proper ancestors of node H A B D H C E I J F G proper descendants of node C 6

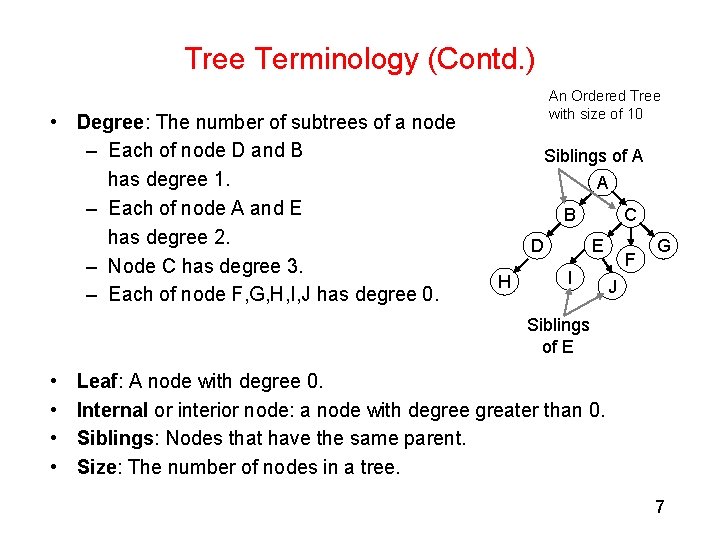
Tree Terminology (Contd. ) • Degree: The number of subtrees of a node – Each of node D and B has degree 1. – Each of node A and E has degree 2. – Node C has degree 3. – Each of node F, G, H, I, J has degree 0. An Ordered Tree with size of 10 Siblings of A A B D H C E I F G J Siblings of E • • Leaf: A node with degree 0. Internal or interior node: a node with degree greater than 0. Siblings: Nodes that have the same parent. Size: The number of nodes in a tree. 7

Tree Terminology (Contd. ) • Level (or depth) of a node v: The length of the path from the root to v. • Height of a node v: The length of the longest path from v to a leaf node. – The height of a tree is the height of its root node. – By definition the height of an empty tree is -1. • The height of the tree is 4. Level 0 A • The height of node C is 3. B D H E F I Level 1 C J G Level 2 Level 3 k Level 4 8

Importance of Trees • Trees are very important data structures in computing. • They are suitable for: – Hierarchical structure representation, e. g. , • File directory. • Organizational structure of an institution. • Class inheritance tree. – Problem representation, e. g. , • Expression tree. • Decision tree. – Efficient algorithmic solutions, e. g. , • Search trees. • Efficient priority queues via heaps. 9

Implementation of Trees • In a general tree, there is no limit to the number of children that a node can have. • Representing a general tree by linked lists: – Each node has a linked list of the subtrees of that node. – Each element of the linked list is a subtree of the current node public class protected //. . . } General. Tree extends Abstract. Container { Object key ; int degree ; My. Linked. List list ; 10

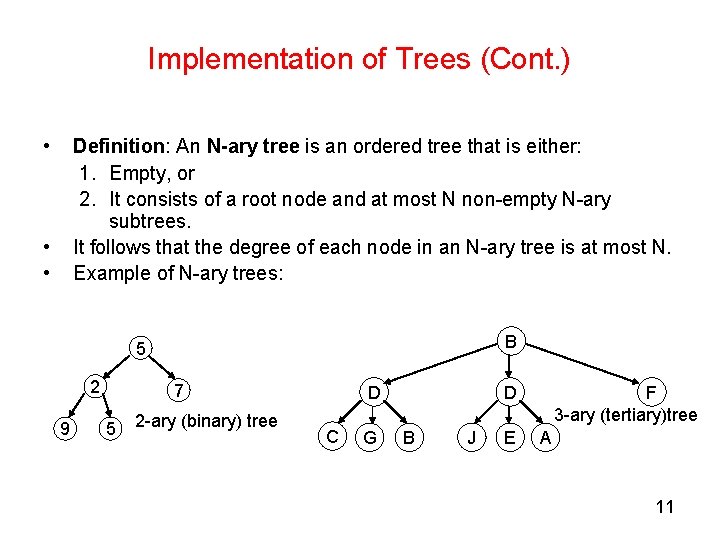
Implementation of Trees (Cont. ) • Definition: An N-ary tree is an ordered tree that is either: 1. Empty, or 2. It consists of a root node and at most N non-empty N-ary subtrees. It follows that the degree of each node in an N-ary tree is at most N. Example of N-ary trees: • • B 5 2 9 7 5 2 -ary (binary) tree D C G F 3 -ary (tertiary)tree D B J E A 11

Implementation of Trees (Cont. ) public class protected Nary. Tree extends Abstract. Container { Object key ; int degree ; Nary. Tree[ ] subtree ; public Nary. Tree(int degree){ key = null ; this. degree = degree ; subtree = null ; } public Nary. Tree(int degree, Object key){ this. key = key ; this. degree = degree ; subtree = new Nary. Tree[degree] ; for(int i = 0; i < degree; i++) subtree[i] = new Nary. Tree(degree); } //. . . } 12

Binary Trees • • Definition: A binary tree is an N-ary tree for which N = 2. Thus, a binary tree is either: 1. An empty tree, or 2. A tree consisting of a root node and at most two non-empty binary subtrees. Example: 5 2 9 7 5 13

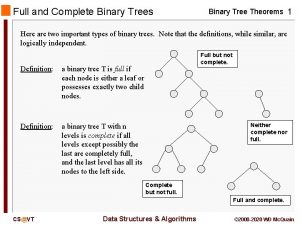
Binary Trees (Contd. ) • Definition: A full binary tree is either an empty binary tree or a binary tree in which every node is either a leaf node or an internal node with two children. • Definition: A complete binary tree is either an empty binary tree or a binary tree in which: 1. Each level k, k > 0, other than the last level contains the maximum number of nodes for that level, that is 2 k. 2. The last level may or may not contain the maximum number of nodes. 3. If a slot with a missing node is encountered when scanning the last level in a left to right direction, then all remaining slots in the level must be empty. 14

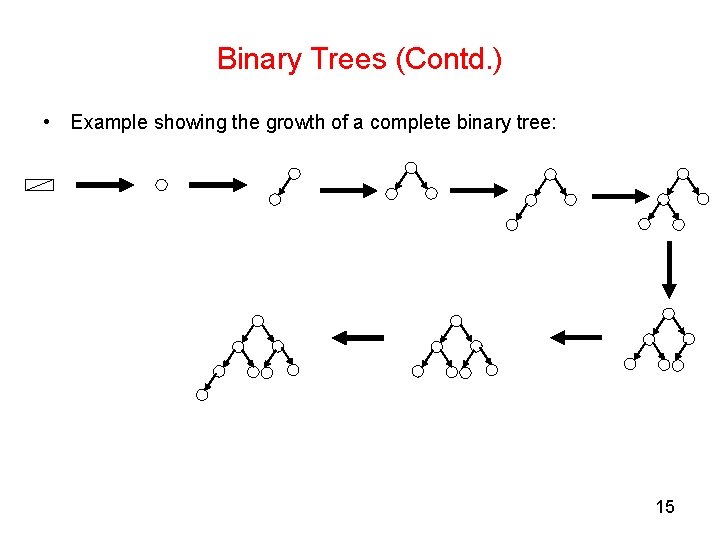
Binary Trees (Contd. ) • Example showing the growth of a complete binary tree: 15

Binary Trees (Contd. ) • What is the maximum height of a binary tree with n elements? n– 1 • What is the minimum height of a binary tree with n elements? log(n) • What is the minimum and maximum heights of a complete binary tree? Both are log(n) • What is the minimum and maximum heights of a full binary tree? log(n) and n/2 16

Binary Trees Implementation public class Binary. Tree extends Abstract. Container{ protected Object key ; protected Binary. Tree left, right ; public Binary. Tree(Object key, Binary. Tree left, Binary. Tree right){ this. key = key ; this. left = left ; this. right = right ; } public Binary. Tree( ) { this(null, null) ; } public Binary. Tree(Object key){ this(key, new Binary. Tree( )); } //. . . } left key right Example: A binary tree representing a + (b - c) * d + a * - b d c 17

Binary Trees Implementation (Contd. ) public boolean is. Empty( ){ return key == null ; } public boolean is. Leaf( ){ return ! is. Empty( ) && left. is. Empty( ) && right. is. Empty( ) ; } public Object get. Key( ){ if(is. Empty( )) throw new Invalid. Operation. Exception( ) ; else return key ; } public int get. Height( ){ if(is. Empty( )) return -1 ; else return 1 + Math. max(left. get. Height( ), right. get. Height( )) ; } public void attach. Key(Object obj){ if(! is. Empty( )) throw new Invalid. Operation. Exception( ) ; else{ key = obj ; left = new Binary. Tree( ) ; What is the complexity of right = new Binary. Tree( ) ; each of these operations? } } 18

Binary Trees Implementation (Contd. ) public Object detach. Key( ){ if(! is. Leaf( )) throw new Invalid. Operation. Exception( ) ; else { Object obj = key ; key = null ; left = null ; What is the complexity of right = null ; each of these operations? return obj ; } } public Binary. Tree get. Left( ){ if(is. Empty( )) throw new Invalid. Operation. Exception( ) ; else return left ; } public Binary. Tree get. Right( ){ if(is. Empty( )) throw new Invalid. Operation. Exception( ) ; else return right ; } 19

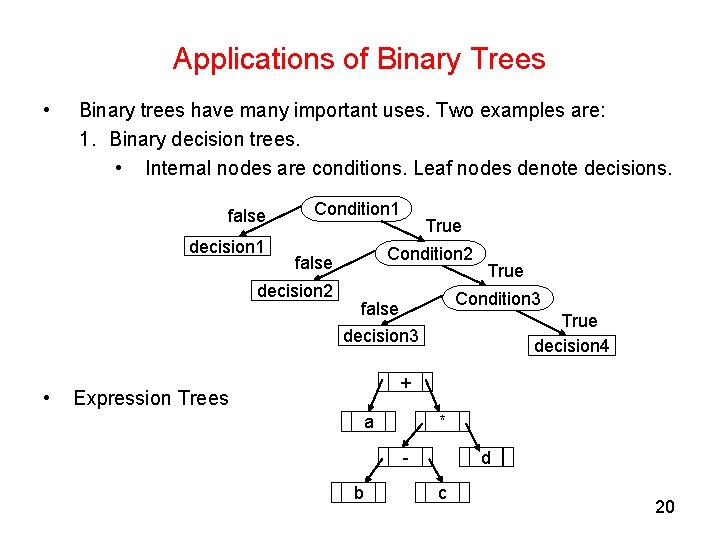
Applications of Binary Trees • Binary trees have many important uses. Two examples are: 1. Binary decision trees. • Internal nodes are conditions. Leaf nodes denote decisions. false decision 1 Condition 1 • Condition 2 false decision 2 True Condition 3 false decision 3 True decision 4 + Expression Trees a * - b d c 20

Binary Search Trees • • • Definition: A binary search tree (BST) is a binary tree that is empty or that satisfies the BST ordering property: 1. The key of each node is greater than each key in the left subtree, if any, of the node. 2. The key of each node is less than each key in the right subtree, if any, of the node. Thus, each key in a BST is unique. Examples: 6 A 2 1 8 4 3 7 5 B 9 C D 21

Importance of BSTs • • BSTs provide good logarithmic time performance in the best and average cases. Average case complexities of using linear data structures compared to BSTs: Data Structure Retrieval Insertion Deletion BST O(log n) FAST Sorted Array O(log n) FAST* O(n) SLOW Sorted Linked List O(n) SLOW *using binary search 22

Implementation of BSTs • The Binary. Search. Tree class inherits the instance variables key, left, and right of the Binary. Tree class: public class Binary. Search. Tree extends Binary. Tree implements Searchable. Container { private Binary. Search. Tree get. Left. BST(){ return (Binary. Search. Tree) get. Left( ) ; } private Binary. Search. Tree get. Right. BST( ){ return (Binary. Search. Tree) get. Right( ) ; } //. . . } What is the complexity of each of these operations? 23

Implementation of BSTs (Cont. ) • The find method of the Binary. Search. Tree class: public Comparable find(Comparable comparable) { if(is. Empty()) return null; Comparable key = (Comparable) get. Key(); if(comparable. compare. To(key)==0) return key; else if (comparable. compare. To(key)<0) return get. Left. BST(). find(comparable); else return get. Right. BST(). find(comparable); } What is the complexity of each of find? 24

Implementation of BSTs (Cont. ) • The find. Min method of the Binary. Search. Tree class: • By the BST ordering property, the minimum key is the key of the left-most node that has an empty left-subtree. public Comparable find. Min() { if(is. Empty()) return null; if(get. Left. BST(). is. Empty()) return (Comparable)get. Key(); else return get. Left. BST(). find. Min(); } What is the complexity of each of find. Min? 25

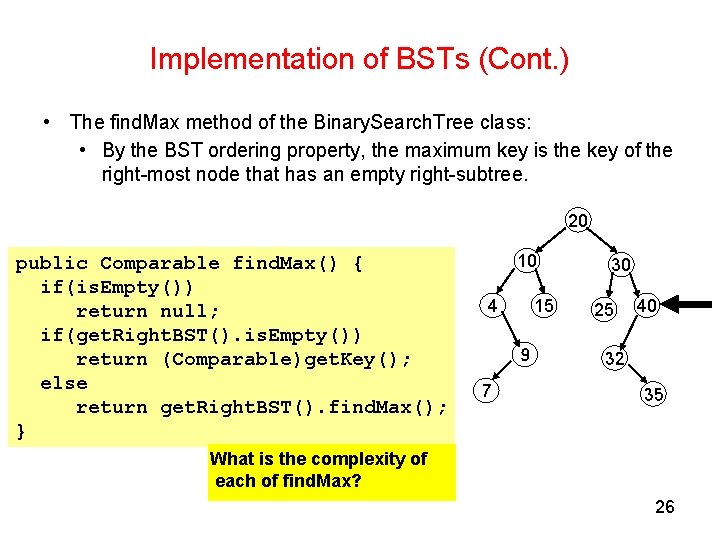
Implementation of BSTs (Cont. ) • The find. Max method of the Binary. Search. Tree class: • By the BST ordering property, the maximum key is the key of the right-most node that has an empty right-subtree. 20 public Comparable find. Max() { if(is. Empty()) return null; if(get. Right. BST(). is. Empty()) return (Comparable)get. Key(); else return get. Right. BST(). find. Max(); } 10 4 15 9 7 30 25 40 32 35 What is the complexity of each of find. Max? 26

Insertion in BSTs • By the BST ordering property, a new node is always inserted as a leaf node. • The insert method, given in the next page, recursively finds an appropriate empty subtree to insert the new key. It then transforms this empty subtree into a leaf node by invoking the attach. Key method: public void attach. Key(Object obj) { if(!is. Empty()) throw new Invalid. Operation. Exception(); else { key = obj; left = new Binary. Search. Tree(); right = new Binary. Search. Tree(); } } 27

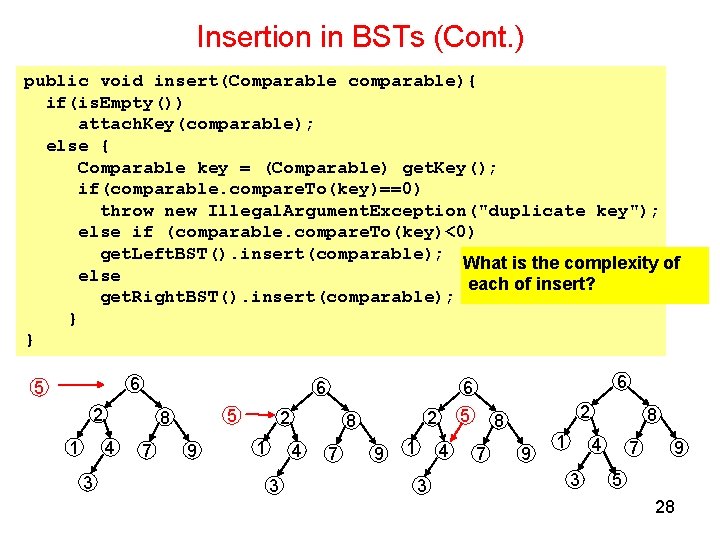
Insertion in BSTs (Cont. ) public void insert(Comparable comparable){ if(is. Empty()) attach. Key(comparable); else { Comparable key = (Comparable) get. Key(); if(comparable. compare. To(key)==0) throw new Illegal. Argument. Exception("duplicate key"); else if (comparable. compare. To(key)<0) get. Left. BST(). insert(comparable); What is the complexity of else each of insert? get. Right. BST(). insert(comparable); } } 6 5 6 2 1 4 3 5 8 7 9 2 1 3 7 5 2 8 4 6 6 9 1 4 3 2 8 7 9 1 8 4 3 7 9 5 28

Deletion in BSTs • There are three cases: 1. The node to be deleted is a leaf node. 2. The node to be deleted has one non-empty child. 3. The node to be deleted has two non-empty children. CASE 1: DELETING A LEAF NODE Convert the leaf node into an empty tree by using the detach. Key method: // In Binary Tree class public Object detach. Key( ){ if(! is. Leaf( )) throw new Invalid. Operation. Exception( ) ; else { Object obj = key ; key = null ; left = null ; right = null ; return obj ; } } 29

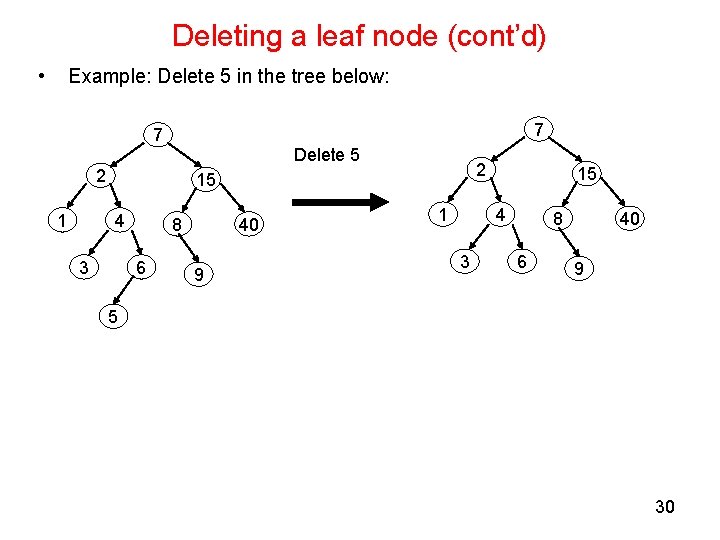
Deleting a leaf node (cont’d) • Example: Delete 5 in the tree below: 7 7 Delete 5 2 15 4 3 8 6 40 9 1 15 4 3 8 6 40 9 5 30

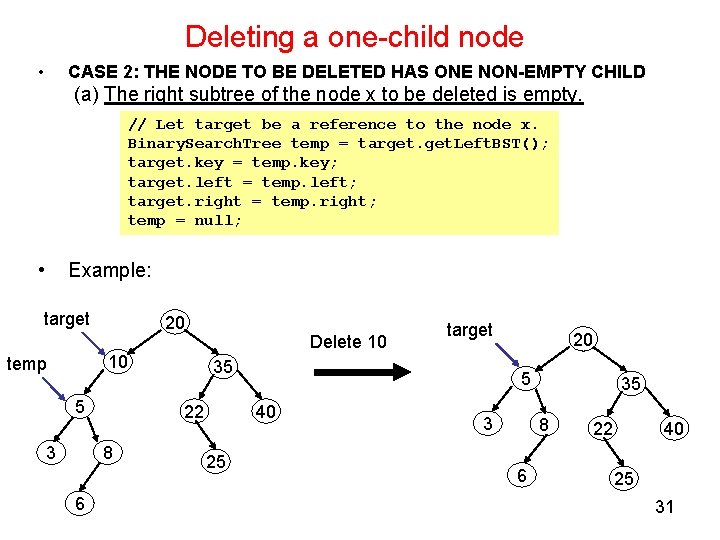
Deleting a one-child node • CASE 2: THE NODE TO BE DELETED HAS ONE NON-EMPTY CHILD (a) The right subtree of the node x to be deleted is empty. // Let target be a reference to the node x. Binary. Search. Tree temp = target. Left. BST(); target. key = temp. key; target. left = temp. left; target. right = temp. right; temp = null; • Example: target 20 10 temp 5 3 target 35 22 8 6 Delete 10 5 40 25 20 3 35 8 6 22 40 25 31

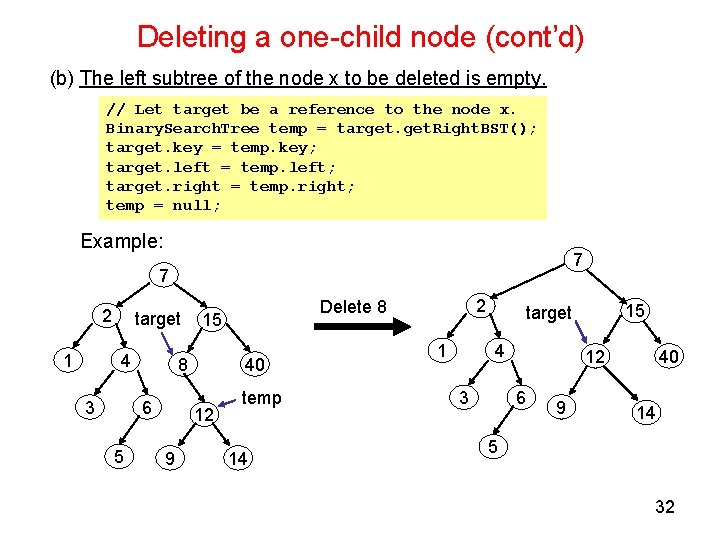
Deleting a one-child node (cont’d) (b) The left subtree of the node x to be deleted is empty. // Let target be a reference to the node x. Binary. Search. Tree temp = target. Right. BST(); target. key = temp. key; target. left = temp. left; target. right = temp. right; temp = null; Example: 7 7 2 1 target 4 3 8 6 5 40 12 9 2 Delete 8 15 temp 14 1 15 target 4 3 12 6 9 40 14 5 32

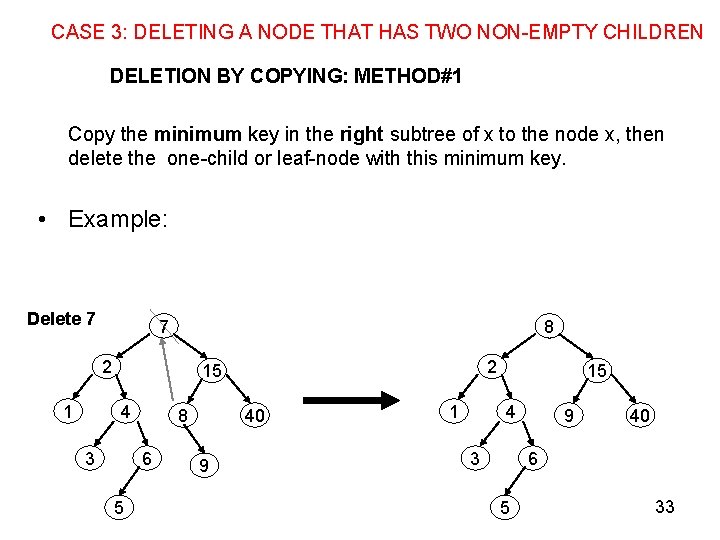
CASE 3: DELETING A NODE THAT HAS TWO NON-EMPTY CHILDREN DELETION BY COPYING: METHOD#1 Copy the minimum key in the right subtree of x to the node x, then delete the one-child or leaf-node with this minimum key. • Example: Delete 7 7 8 2 15 4 3 8 6 5 40 9 1 15 4 3 9 40 6 5 33

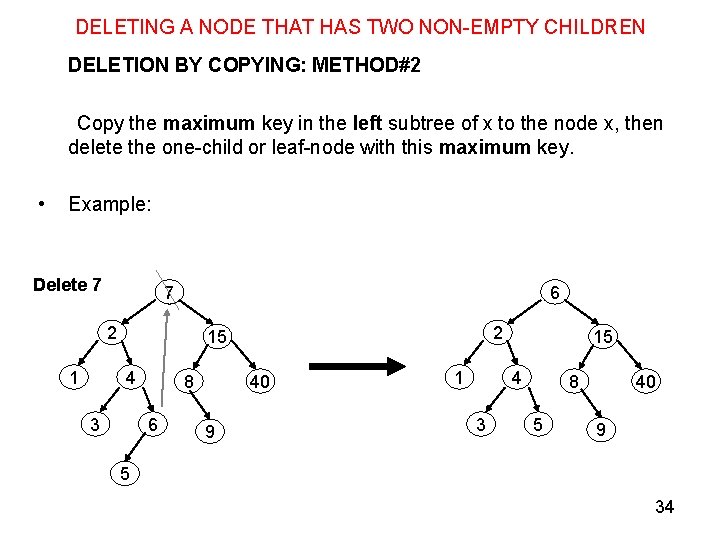
DELETING A NODE THAT HAS TWO NON-EMPTY CHILDREN DELETION BY COPYING: METHOD#2 Copy the maximum key in the left subtree of x to the node x, then delete the one-child or leaf-node with this maximum key. • Example: Delete 7 7 6 2 15 4 3 8 6 40 9 1 15 4 3 8 5 40 9 5 34

Two-child deletion method#1 code // find the minimum key in the right subtree of the target node Comparable min = target. Right. BST(). find. Min(); // copy the minimum value to the target. key = min; // delete the one-child or leaf node having the min target. Right. BST(). withdraw(min); All the different cases for deleting a node are handled in the withdraw (Comparable key) method of Binary. Search. Tree class What is the complexity of each of the delete method? 35