Trees Chapter 7 1 What is a Tree

Trees Chapter 7 1

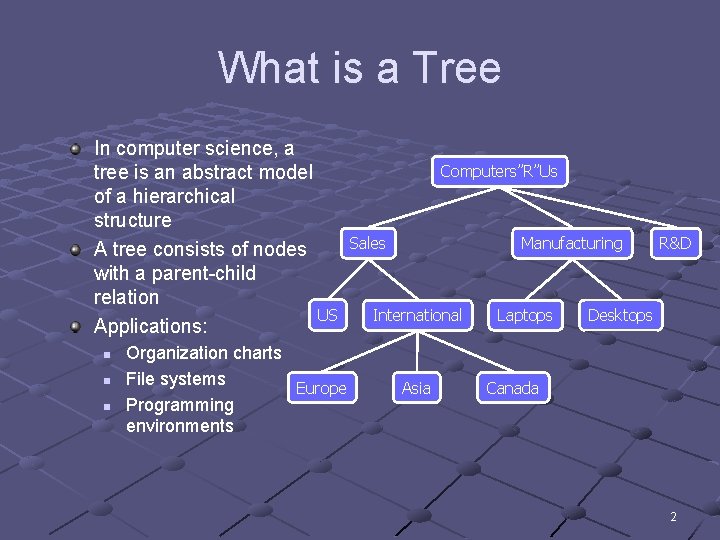
What is a Tree In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes with a parent-child relation US Applications: n n n Organization charts File systems Europe Programming environments Computers”R”Us Sales Manufacturing International Asia Laptops R&D Desktops Canada 2

Outline • Recursive Structure Definitions • Tree Terminology • Binary Tree Interface • Example - Expression Trees • Binary Tree Implementation • Tree Traversals • Tree Property-based methods 3

List Definition - Recursive • A list is either empty or it contains a head element and a sublist where the sublist must be a list. 4

Tree Definition - Recursive • A tree is either empty or it consists of an element called the root, and a (possibly empty) list of subtrees, where each subtree is a tree. • The term node is used to refer to an element at a particular location in a tree. 5

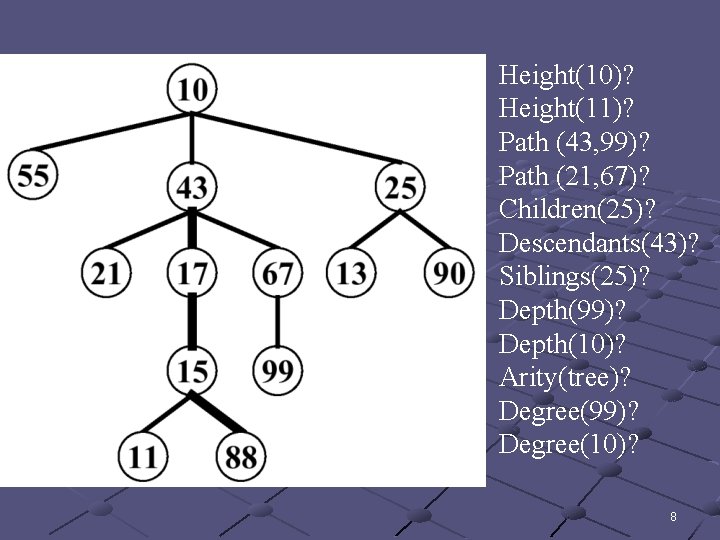
• A path is the unique shortest sequence of edges from a node to an ancestor. • The length of a path is the number of edges in it. • The height of a node = tree. height – length(path(root, node)). • The height of a tree is the height of its root. • The depth (level) of a node is the length of the path from the root to the node. • The degree of a node is the number of children it has. • The degree (arity) of a tree is the maximum degree of its nodes. 6

• If node N 2 is the root of a direct subtree of node N 1 , then node N 2 is a child of node N 1 and node N 1 is the parent of node N 2. • The root node of a tree has no parent node in that tree. • A node N 1 is an ancestor of a node N 2 , if N 1 is the parent of node N 2 or if N 1 is the ancestor of a parent of N 2 (this is a recursive definition: ancestors(N) = parent(N) + ancestors(parent(N))). • A node N 2 is a descendent of a node N 1 , if N 1 is an ancestor of node N 2. • A node with no children is called a leaf node. • A node with children is called an interior node. • Two nodes are siblings if they have the same parent. 7

Height(10)? Height(11)? Path (43, 99)? Path (21, 67)? Children(25)? Descendants(43)? Siblings(25)? Depth(99)? Depth(10)? Arity(tree)? Degree(99)? Degree(10)? 8

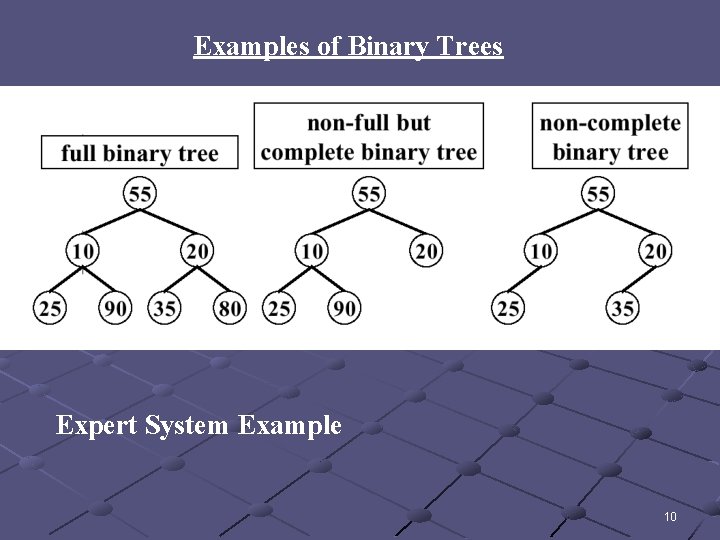
• A binary tree is a tree in which nodes can have a maximum of 2 children. • A binary tree is oriented if every node with 2 children differentiates between the children by calling them the left child and right child and every node with one child designates it either as a left child or right child. • A node in a binary tree is full if it has arity 2. • A full binary tree of height h has leaves only on level h and each of its interior nodes is full. • A complete binary tree of height h is a full binary tree of height h with 0 or more of the rightmost leaves of level h removed. 9

Examples of Binary Trees Expert System Example 10

Binary Tree Traversals There are four common binary tree traversals: – Preorder: process root then left subtree then right subtree – Inorder: process left subtree then root then right subtree – Postorder: process left subtree then right subtree then root – Levelorder: process nodes of level i, before processing nodes of level i + 1 11

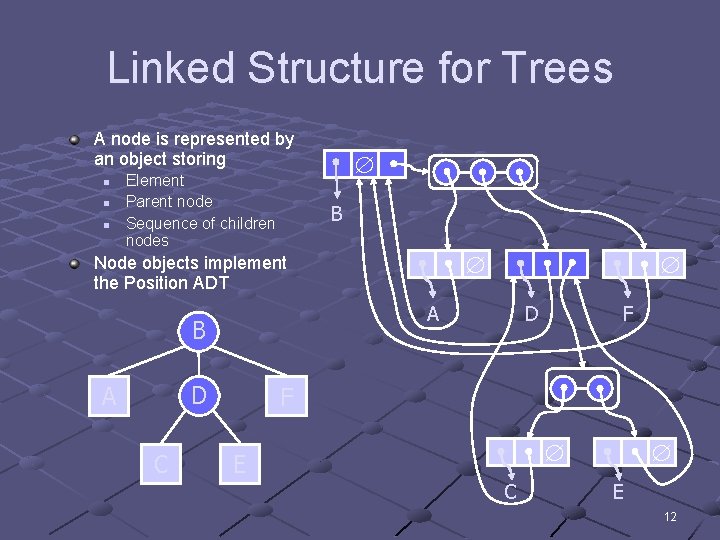
Linked Structure for Trees A node is represented by an object storing n n n Element Parent node Sequence of children nodes B Node objects implement the Position ADT A B D A C D F F E C E 12

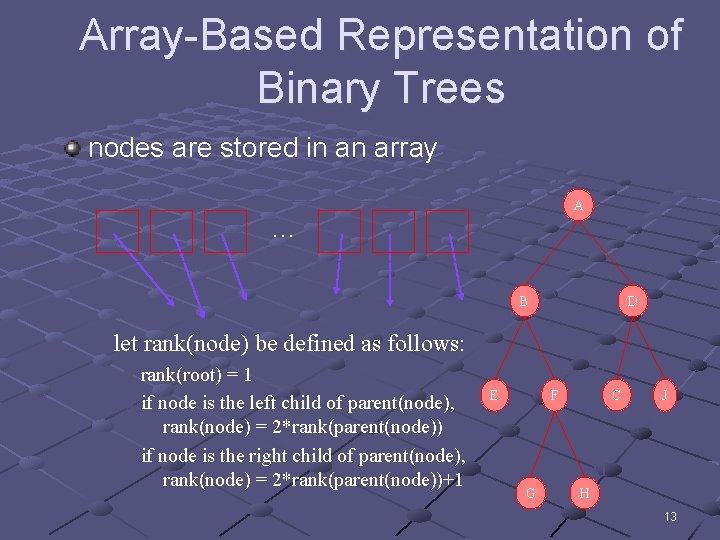
Array-Based Representation of Binary Trees nodes are stored in an array 1 A … 2 3 B n D let rank(node) be defined as follows: n n n 4 rank(root) = 1 if node is the left child of parent(node), rank(node) = 2*rank(parent(node)) if node is the right child of parent(node), rank(node) = 2*rank(parent(node))+1 5 E 6 7 C F 10 J 11 G H 13

Arithmetic Expression Tree Binary tree associated with an arithmetic expression n n internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a 3 b 1 14

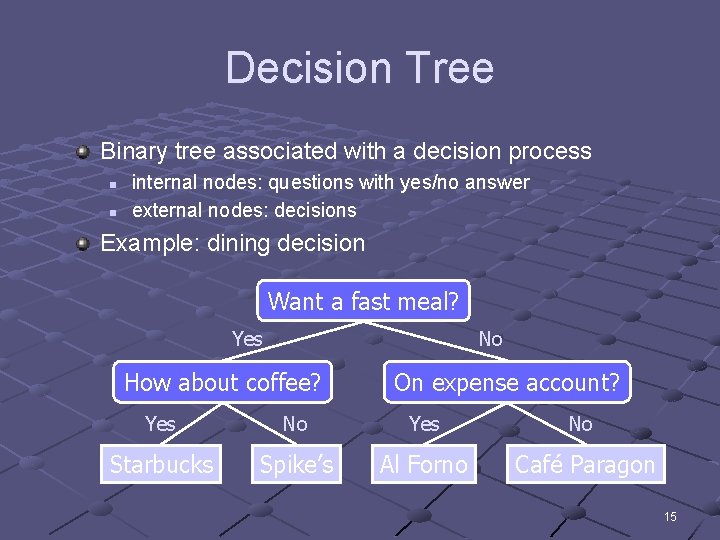
Decision Tree Binary tree associated with a decision process n n internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon 15

Print Arithmetic Expressions Specialization of an inorder traversal n n n print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 3 1 b Algorithm print. Expression(v) if has. Left (v) print(“(’’) in. Order (left(v)) print(v. element ()) if has. Right (v) in. Order (right(v)) print (“)’’) ((2 (a - 1)) + (3 b)) 16

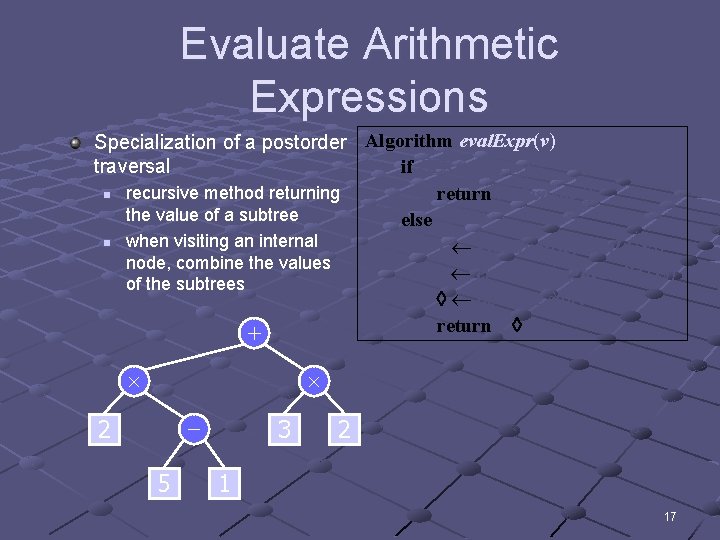
Evaluate Arithmetic Expressions Specialization of a postorder Algorithm eval. Expr(v) traversal if is. External (v) n recursive method returning return v. element () the value of a subtree else n when visiting an internal x eval. Expr(left. Child (v)) node, combine the values y eval. Expr(right. Child (v)) of the subtrees operator stored at v return x y + - 2 5 3 2 1 17