Trees and Binary Trees The class notes are

Trees and Binary Trees The class notes are a compilation and edition from many sources. The instructor does not claim intellectual property or ownership of the lecture notes.
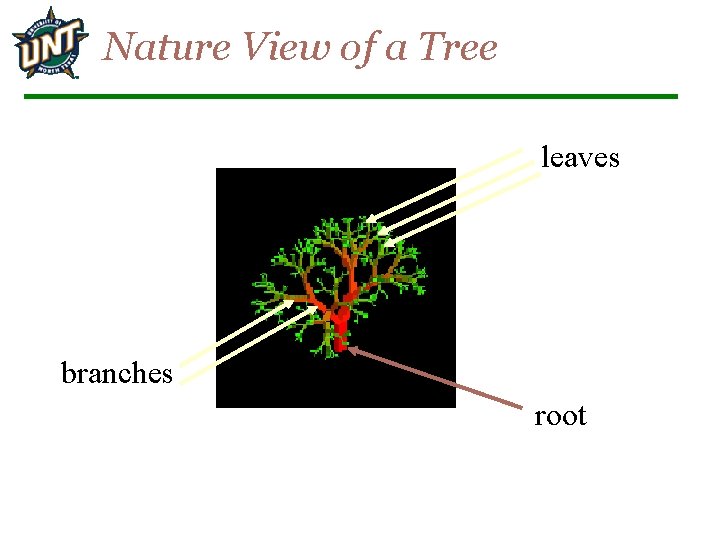
Nature View of a Tree leaves branches root
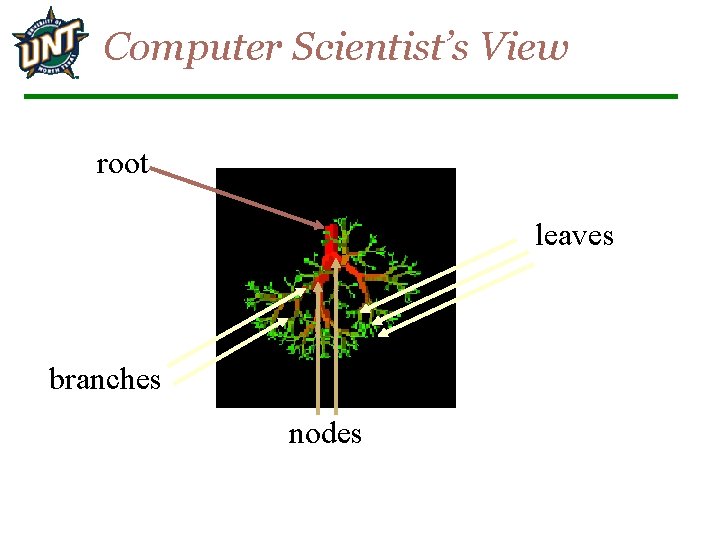
Computer Scientist’s View root leaves branches nodes
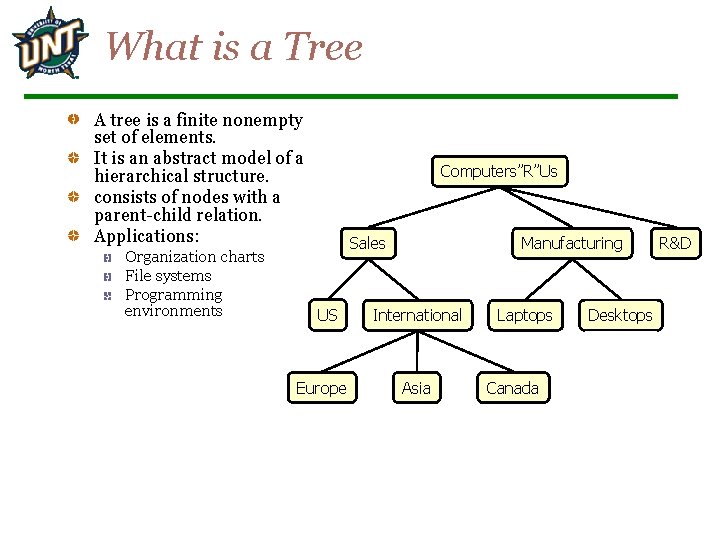
What is a Tree A tree is a finite nonempty set of elements. It is an abstract model of a hierarchical structure. consists of nodes with a parent-child relation. Applications: Organization charts File systems Programming environments Computers”R”Us Sales US Europe Manufacturing International Asia Laptops Canada Desktops R&D
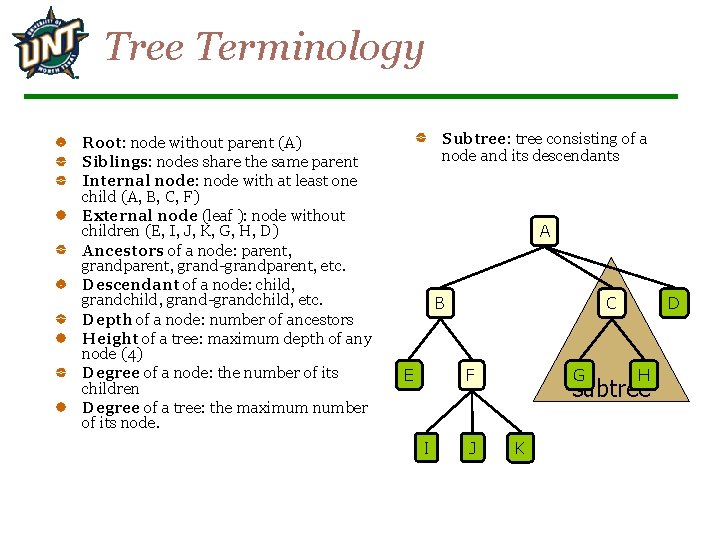
Tree Terminology Root: node without parent (A) Siblings: nodes share the same parent Internal node: node with at least one child (A, B, C, F) External node (leaf ): node without children (E, I, J, K, G, H, D) Ancestors of a node: parent, grand-grandparent, etc. Descendant of a node: child, grand-grandchild, etc. Depth of a node: number of ancestors Height of a tree: maximum depth of any node (4) Degree of a node: the number of its children Degree of a tree: the maximum number of its node. Subtree: tree consisting of a node and its descendants A E F I D C B J G H subtree K

Introduction (3/8) Some Terminology node: the item of information plus the branches to each node. degree: the number of subtrees of a node degree of a tree: the maximum of the degree of the nodes in the tree. terminal nodes (or leaf): nodes that have degree zero nonterminal nodes: nodes that don’t belong to terminal nodes. children: the roots of the subtrees of a node X are the children of X parent: X is the parent of its children.

Introduction (4/8) Some Terminology (cont’d) siblings: children of the same parent are said to be siblings. Ancestors of a node: all the nodes along the path from the root to that node. The level of a node: defined by letting the root be at level one. If a node is at level l, then it children are at level l+1. Height (or depth): the maximum level of any node in the tree
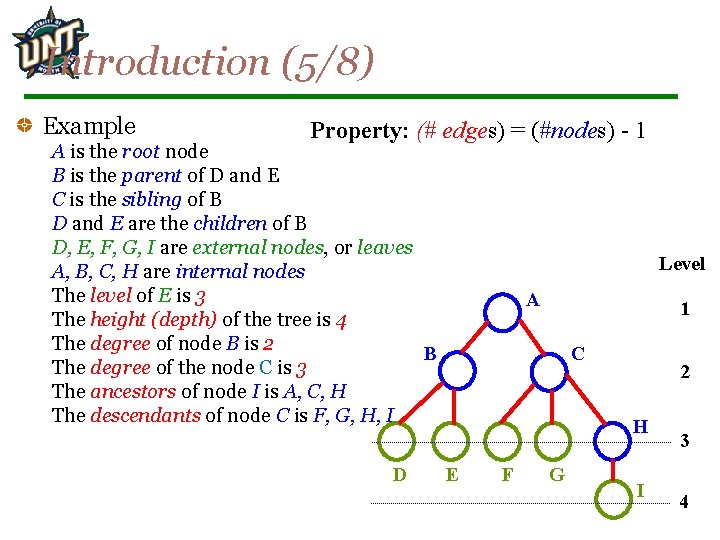
Introduction (5/8) Example Property: (# edges) = (#nodes) - 1 A is the root node B is the parent of D and E C is the sibling of B D and E are the children of B D, E, F, G, I are external nodes, or leaves A, B, C, H are internal nodes The level of E is 3 The height (depth) of the tree is 4 The degree of node B is 2 B The degree of the node C is 3 The ancestors of node I is A, C, H The descendants of node C is F, G, H, I D Level A 1 C 2 H E F G I 3 4

Tree ADT We use positions to abstract nodes Generic methods: integer size() boolean is. Empty() object. Iterator elements() position. Iterator positions() Accessor methods: position root() position parent(p) position. Iterator children(p) Query methods: boolean is. Internal(p) boolean is. External(p) boolean is. Root(p) Update methods: swap. Elements(p, q) object replace. Element(p, o) Additional update methods may be defined by data structures implementing the Tree ADT
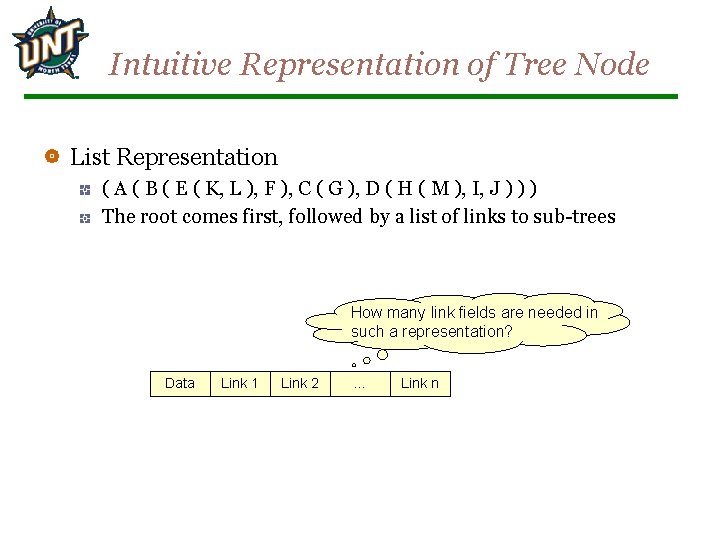
Intuitive Representation of Tree Node List Representation ( A ( B ( E ( K, L ), F ), C ( G ), D ( H ( M ), I, J ) ) ) The root comes first, followed by a list of links to sub-trees How many link fields are needed in such a representation? Data Link 1 Link 2 … Link n

List Representation of Trees The tree in previous slide could be written as (A (B (E (K, L), F), C(G), D(H (M), I, J))) A 0 B F 0 E K C L 0 G 0 D I H M 0 J 0

List Representation of Trees The tree in previous slide could be written as (A (B (E (K, L), F), C(G), D(H (M), I, J)))
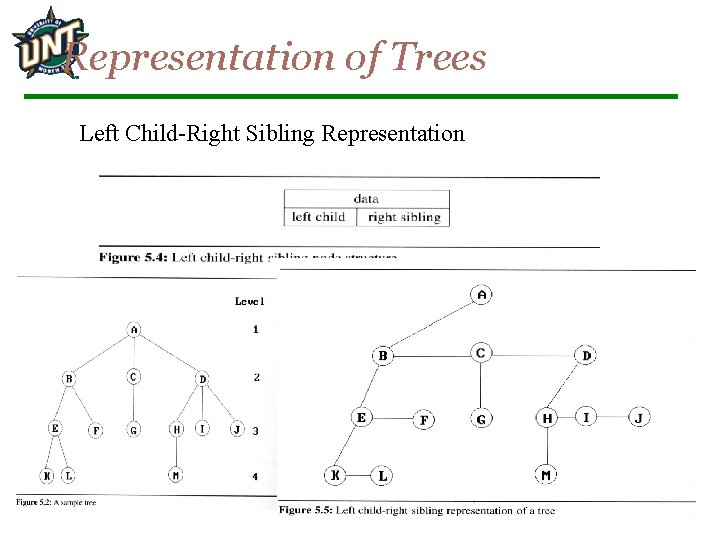
Representation of Trees Left Child-Right Sibling Representation

Binary Tree A tree in which every node can have a maximum of two children is called as Binary Tree.
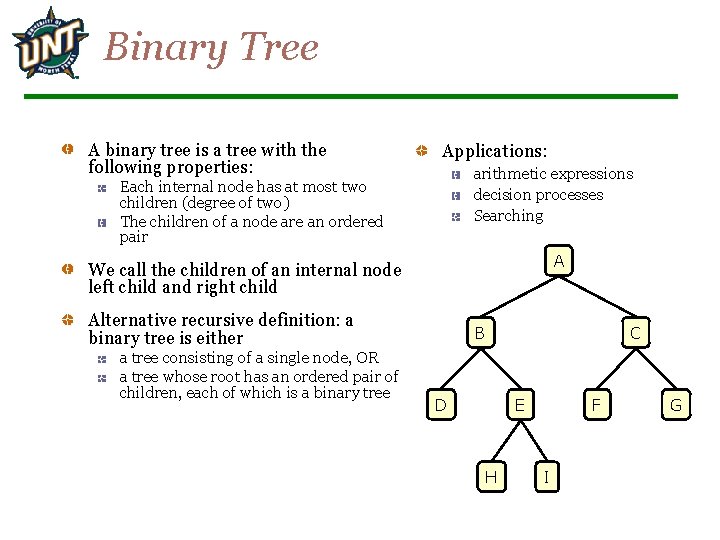
Binary Tree A binary tree is a tree with the following properties: Applications: arithmetic expressions decision processes Searching Each internal node has at most two children (degree of two) The children of a node are an ordered pair A We call the children of an internal node left child and right child Alternative recursive definition: a binary tree is either a tree consisting of a single node, OR a tree whose root has an ordered pair of children, each of which is a binary tree B C D F E H I G

Full Binary Tree A binary tree in which every node has either two or zero number of children , every level is completely filled , number of node at any level I in a full binary tree is 2^i is called Full Binary Tree

Full Binary Tree/Perfect Binary Tree A binary tree of height h that contains exactly (2^h)-1 elements is called a full binary tree. Number of nodes = 2 d+1 – 1 Number of leaf nodes = 2 d Where, d – Depth of the tree
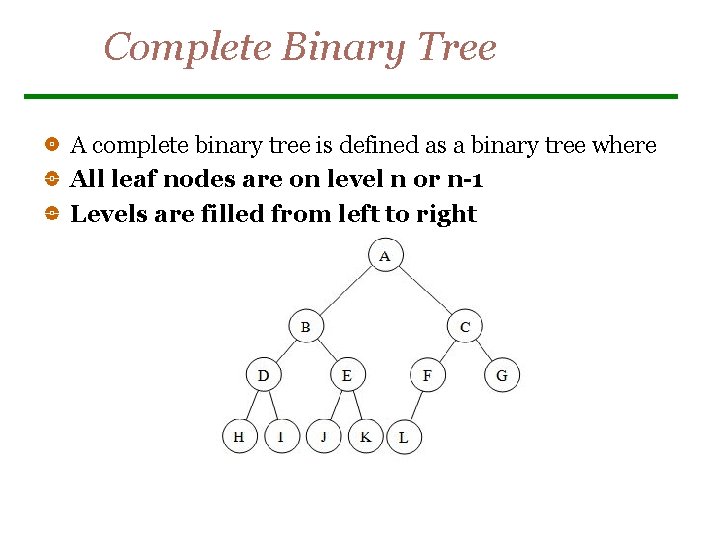
Complete Binary Tree A complete binary tree is defined as a binary tree where All leaf nodes are on level n or n-1 Levels are filled from left to right

Strictly Binary Tree A node will have either two children or no child at all.

Extended Binary Tree Extended binary Tree or 2 tree is a binary tree T, in which each node has zero or two children. Internal nodes. N(I)-7 External nodes. N(E)-8 N(I)=7 N(E)=N(I)+1
![The Properties of Binary Trees Lemma 5. 2 [Maximum number of nodes] 1) 2) The Properties of Binary Trees Lemma 5. 2 [Maximum number of nodes] 1) 2)](http://slidetodoc.com/presentation_image_h2/479743b227ff87db1297c10fae482a1b/image-21.jpg)
The Properties of Binary Trees Lemma 5. 2 [Maximum number of nodes] 1) 2) The maximum number of nodes on level i of a binary tree is 2 i-1, i ≥ 1. The maximum number of nodes in a binary tree of depth k is 2 k – 1, k ≥ 1. Lemma 5. 3 [Relation between number of leaf nodes and nodes of degree 2]: For any non-empty binary tree, T, if n 0 is the number of leaf nodes and n 2 the number of nodes of degree 2, then n 0 = n 2 + 1. Definition: A full binary tree of depth k is a binary tree of depth k having 2 k – 1 nodes, k ≥ 0.
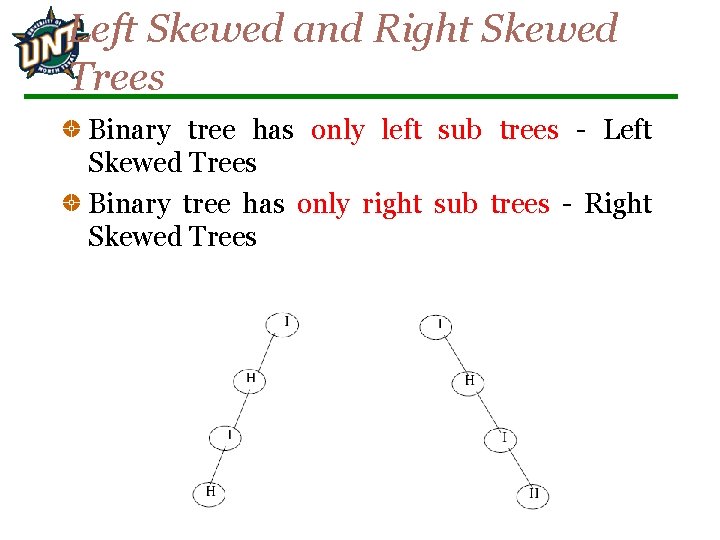
Left Skewed and Right Skewed Trees Binary tree has only left sub trees - Left Skewed Trees Binary tree has only right sub trees - Right Skewed Trees

Binary Tree Representation 1. Sequential representation using arrays 2. List representation using Linked list
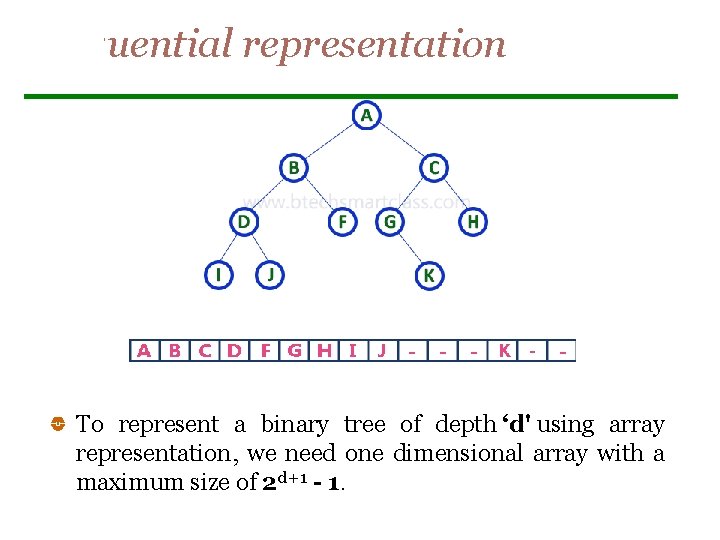
Sequential representation To represent a binary tree of depth ‘d' using array representation, we need one dimensional array with a maximum size of 2 d+1 - 1.

Sequential representation Advantages: Direct access to all nodes (Random access) Disadvantages: Height of tree should be known Memory may be wasted Insertion and deletion of a node is difficult
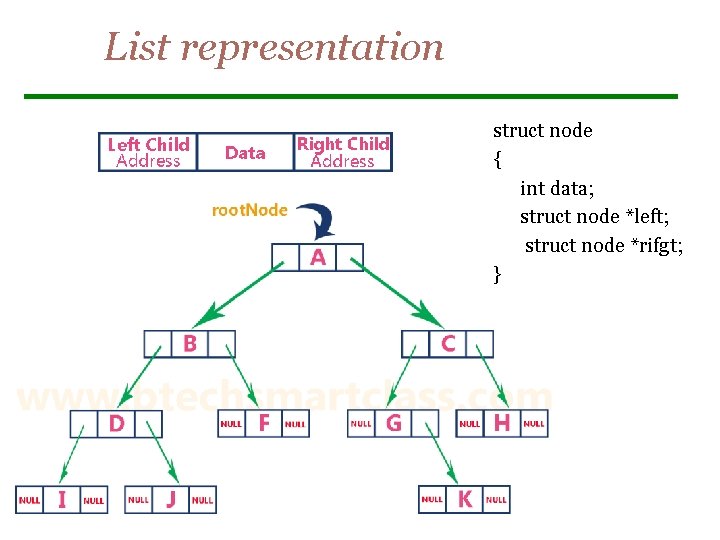
List representation struct node { int data; struct node *left; struct node *rifgt; }

List representation Advantages: Height of tree need not be known No memory wastage Insertion and deletion of a node is done without affecting other nodes Disadvantages: Direct access to node is difficult Additional memory required for storing address of left and right node


MCQ 1) Sequential representation of binary tree uses. A. Array with pointers B. Single linear array C. Two dimensional arrays D. Three dimensional arrays
![MCQ 2) TREE[1]=NULL indicates tree is. . . . A. Overflow B. Underflow C. MCQ 2) TREE[1]=NULL indicates tree is. . . . A. Overflow B. Underflow C.](http://slidetodoc.com/presentation_image_h2/479743b227ff87db1297c10fae482a1b/image-30.jpg)
MCQ 2) TREE[1]=NULL indicates tree is. . . . A. Overflow B. Underflow C. Empty D. Full

MCQ A binary tree whose every node has either zero or two children is called. . . . A. complete binary tree B. binary search tree C. extended binary tree D. data structure

MCQ In a 2 -tree, nodes with 0 children are called. . . A. Exterior node B. Outside node C. Outer node D. External node

MCQ In a extended-binary tree nodes with 2 children are called. . . . A. Interior node B. Domestic node C. Internal node D. Inner node

MCQ A terminal node in a binary tree is called. . . A. Root B. Leaf C. Child D. Branch

Non-Linear Data Structure In a non linear data structure , the Elements are not arranged in sequence. The data members are arranged in any Manner. The data items are not processed one After another. Trees and graphs are examples of non linear data structure.
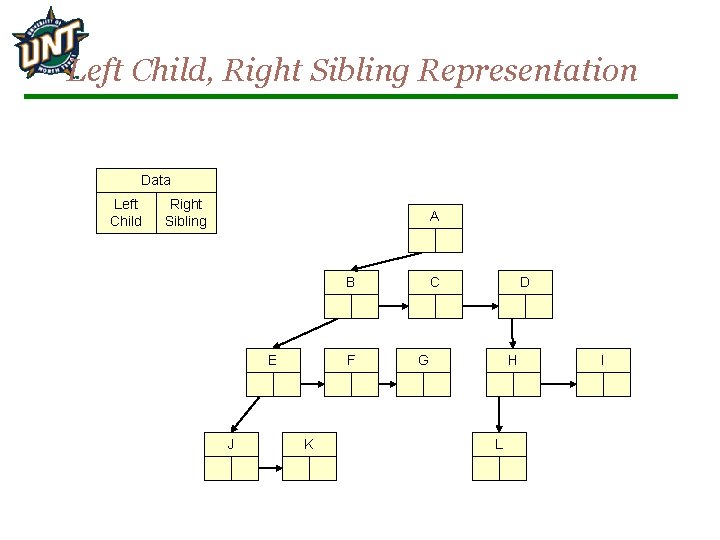
Left Child, Right Sibling Representation Data Left Child Right Sibling A B E J F K C D G H L I

Tree Traversal Two main methods: Breadth First Search(BFS)-Levelwise Depth first Search(DFS)Preorder In-order Post-order Recursive definition Preorder: visit the root traverse in preorder the children (subtrees) Postorder traverse in postorder the children (subtrees) visit the root In-order traverse in order-the children (subtrees) visit the root

Breadth First Search(BFS)-Levelwise Breadth First or Level Order Traversal : 1 2 3 4 5
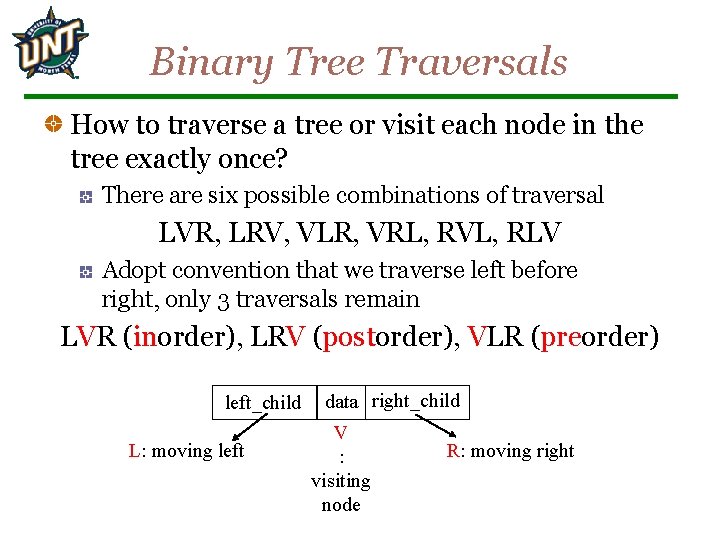
Binary Tree Traversals How to traverse a tree or visit each node in the tree exactly once? There are six possible combinations of traversal LVR, LRV, VLR, VRL, RVL, RLV Adopt convention that we traverse left before right, only 3 traversals remain LVR (inorder), LRV (postorder), VLR (preorder) left_child L: moving left data right_child V : visiting node R: moving right
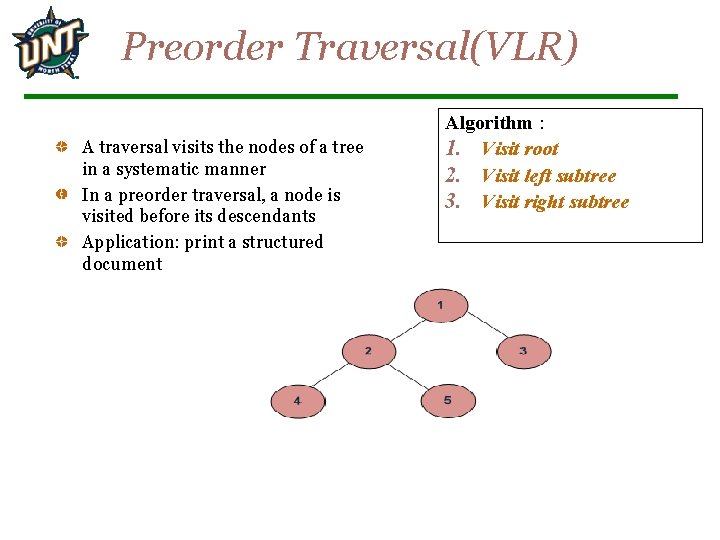
Preorder Traversal(VLR) A traversal visits the nodes of a tree in a systematic manner In a preorder traversal, a node is visited before its descendants Application: print a structured document Algorithm : 1. Visit root 2. Visit left subtree 3. Visit right subtree
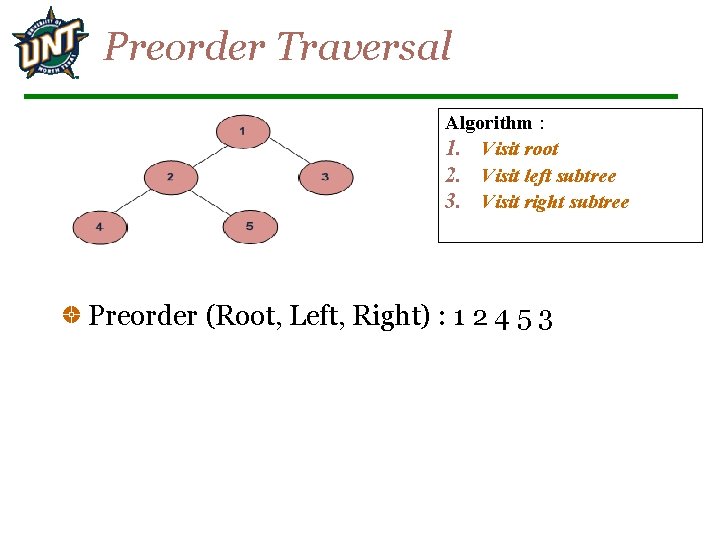
Preorder Traversal Algorithm : 1. Visit root 2. Visit left subtree 3. Visit right subtree Preorder (Root, Left, Right) : 1 2 4 5 3
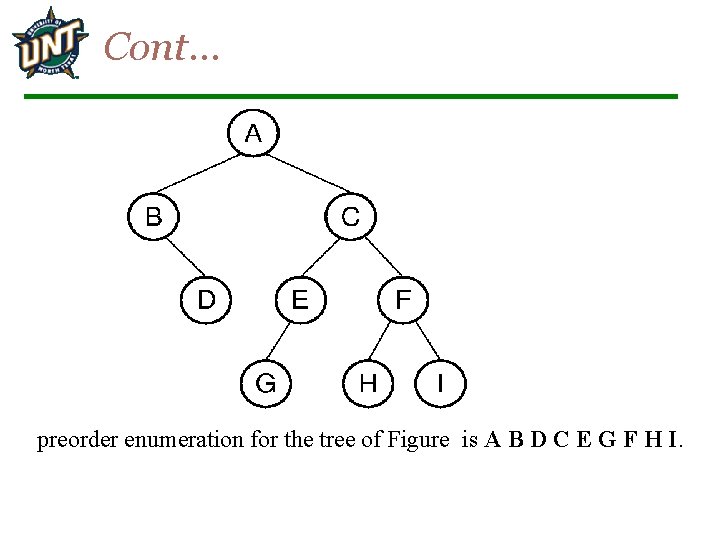
Cont… preorder enumeration for the tree of Figure is A B D C E G F H I.
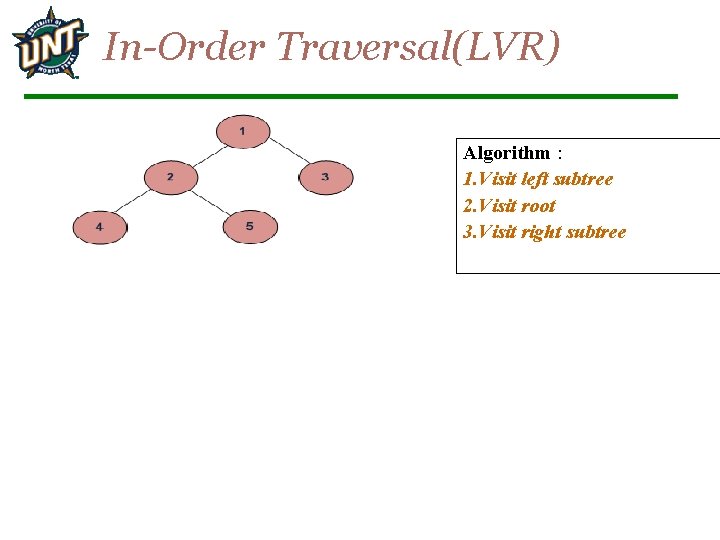
In-Order Traversal(LVR) Algorithm : 1. Visit left subtree 2. Visit root 3. Visit right subtree
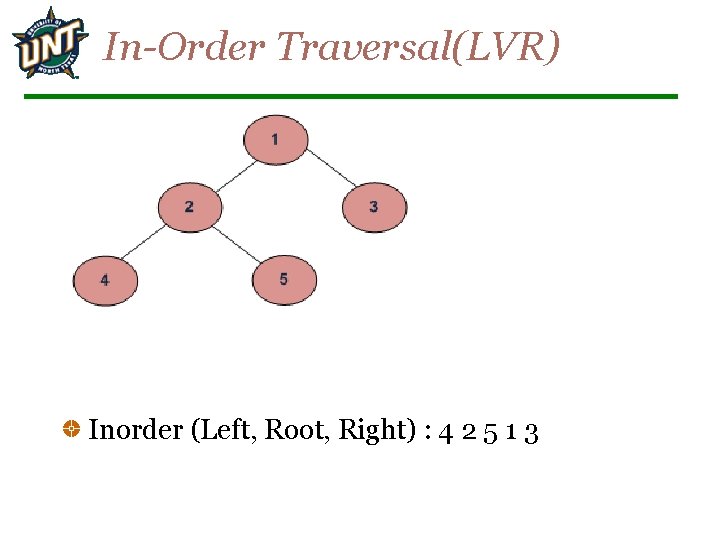
In-Order Traversal(LVR) Inorder (Left, Root, Right) : 4 2 5 1 3
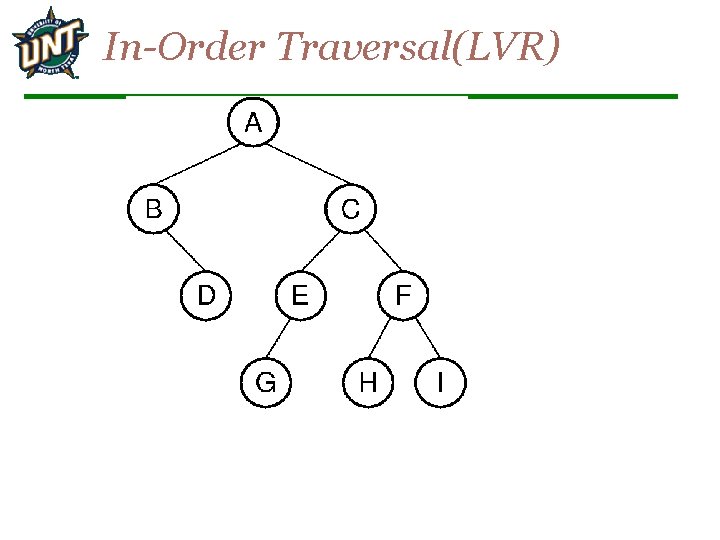
In-Order Traversal(LVR)
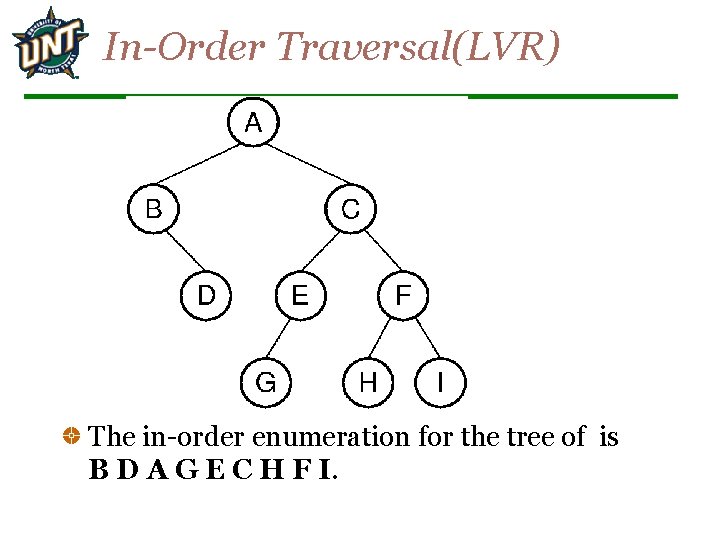
In-Order Traversal(LVR) The in-order enumeration for the tree of is B D A G E C H F I.
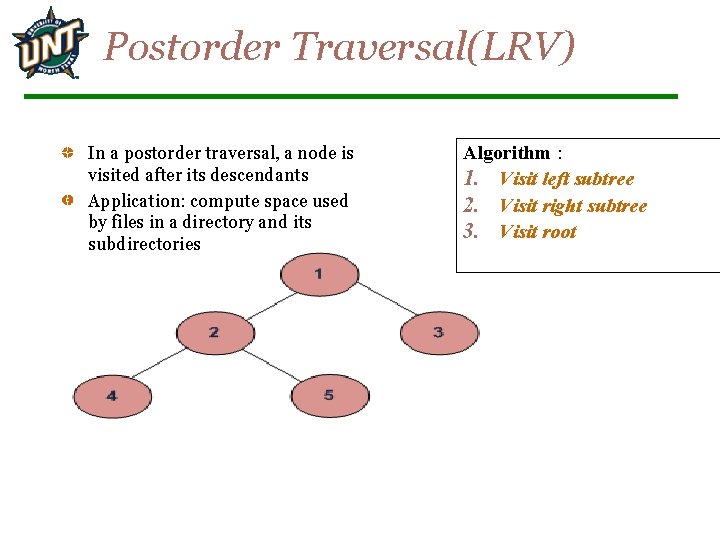
Postorder Traversal(LRV) In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories Algorithm : 1. Visit left subtree 2. Visit right subtree 3. Visit root
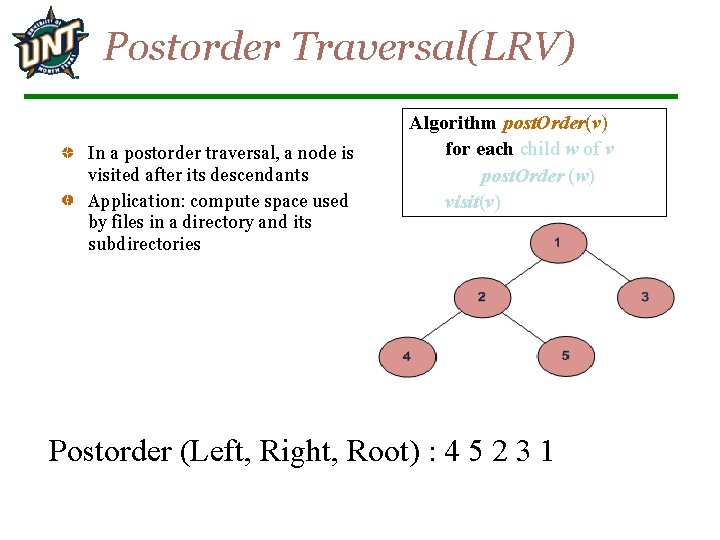
Postorder Traversal(LRV) In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) Postorder (Left, Right, Root) : 4 5 2 3 1
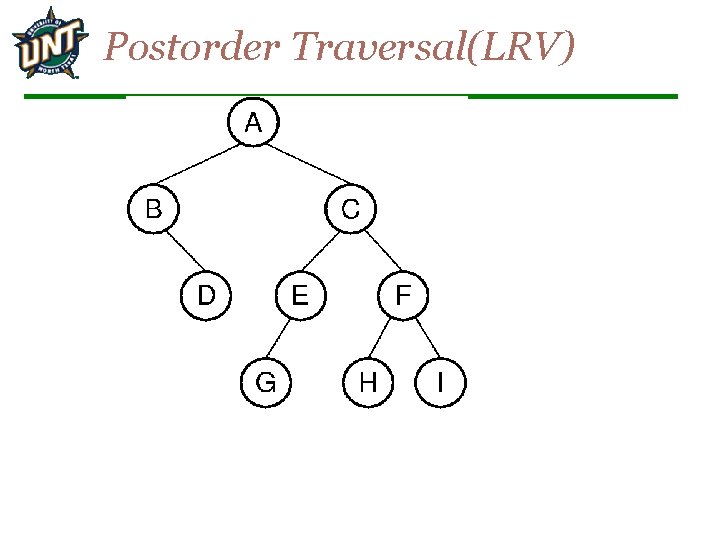
Postorder Traversal(LRV)
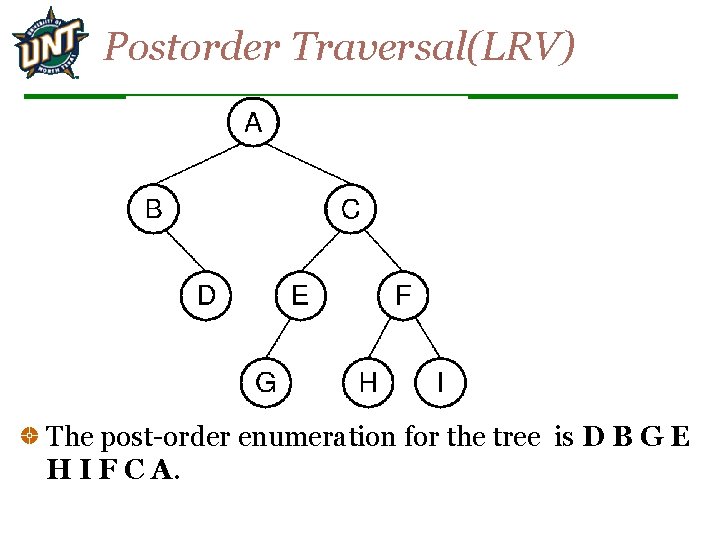
Postorder Traversal(LRV) The post-order enumeration for the tree is D B G E H I F C A.

Binary Tree Traversal implentation class node { public: int data; node *left, *right; }; node * create(node *root); void insert(node *root, node *temp); void dispmenu(node *root); void recdispvlr(node *root); void recdisplvr(node *root); void recdisplrv(node *root); void nonrecvlr(node *root); void nonreclvr(node *root); void nonreclrv(node *root);

Binary Tree Traversal implentation node * node: : create(node *root) { node *temp; temp=new node; temp->left=NULL; temp->right=NULL; cout<<"enter the data"; cin>>temp->data; if(root==NULL) root=temp; else insert(root, temp); return root; }

void node: : insert(node *root, node *temp) { char ch; if(root->left==NULL&&root->right==NULL) { root->left=temp; } else { cout<<"insert data to left(l) or right(r) of "<<root->data; cin>>ch; if(ch=='l') { if(root->left==NULL) root->left=temp; else insert(root->left, temp); } else{ if(root->right==NULL) root->right=temp; else insert(root->right, temp); } }
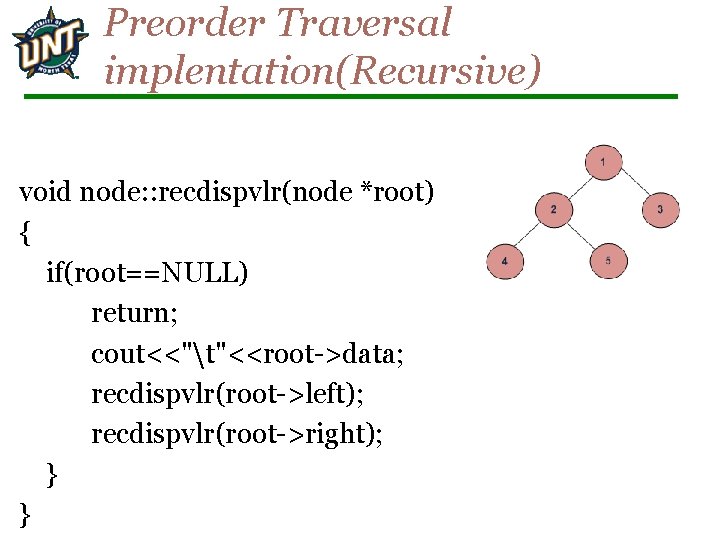
Preorder Traversal implentation(Recursive) void node: : recdispvlr(node *root) { if(root==NULL) return; cout<<"t"<<root->data; recdispvlr(root->left); recdispvlr(root->right); } }
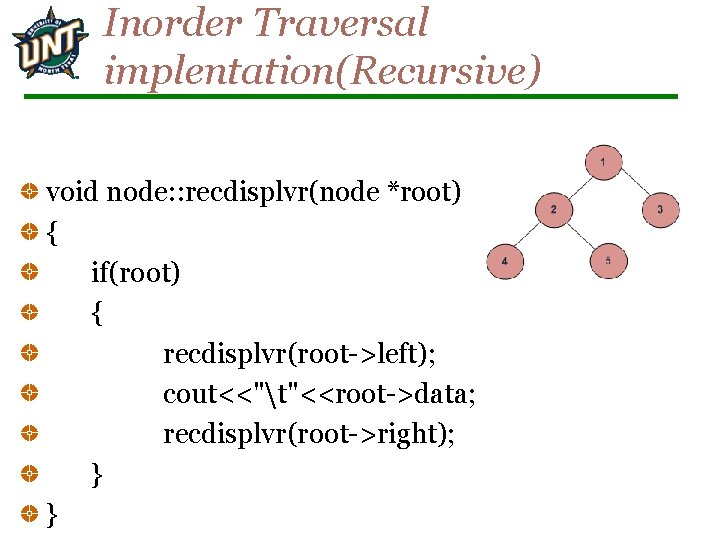
Inorder Traversal implentation(Recursive) void node: : recdisplvr(node *root) { if(root) { recdisplvr(root->left); cout<<"t"<<root->data; recdisplvr(root->right); } }
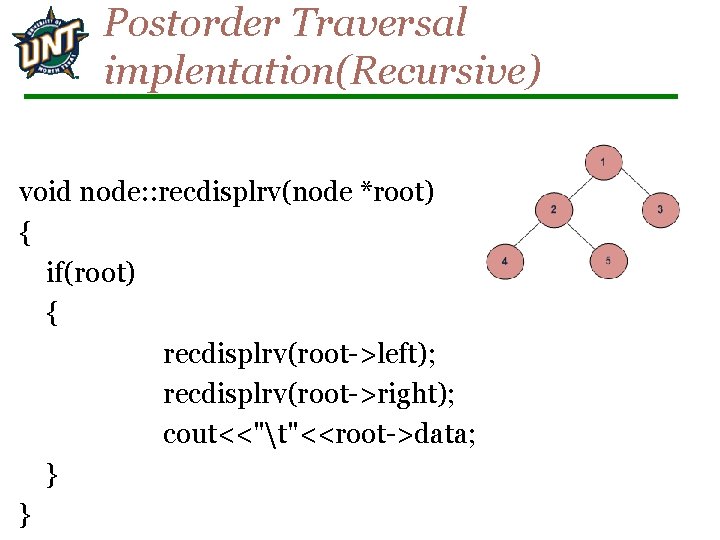
Postorder Traversal implentation(Recursive) void node: : recdisplrv(node *root) { if(root) { recdisplrv(root->left); recdisplrv(root->right); cout<<"t"<<root->data; } }
![Preorder Traversal implentation(Non-Recursive) void node: : nonrecvlr(node *root) { node *stack[100], *temp; int top=-1; Preorder Traversal implentation(Non-Recursive) void node: : nonrecvlr(node *root) { node *stack[100], *temp; int top=-1;](http://slidetodoc.com/presentation_image_h2/479743b227ff87db1297c10fae482a1b/image-57.jpg)
Preorder Traversal implentation(Non-Recursive) void node: : nonrecvlr(node *root) { node *stack[100], *temp; int top=-1; temp=root; while(1) //infinite loop to check the following loop to b true { while(temp) //move down Left. Child fields { top++; stack[top]=temp; cout<<temp->data<<"n"; temp=temp->left; } if(top!=-1) { temp=stack[top]; top--; // cout<<temp->data; temp=temp->right; } else break; } }
Postorder Traversal implentation(Recursive) void node: : recdisplrv(node *root) { if(root) { recdisplrv(root->left); recdisplrv(root->right); cout<<"t"<<root->data; } }

Binary. Tree ADT The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT Additional methods: position left. Child(p) position right. Child(p) position sibling(p) Update methods may be defined by data structures implementing the Binary. Tree ADT
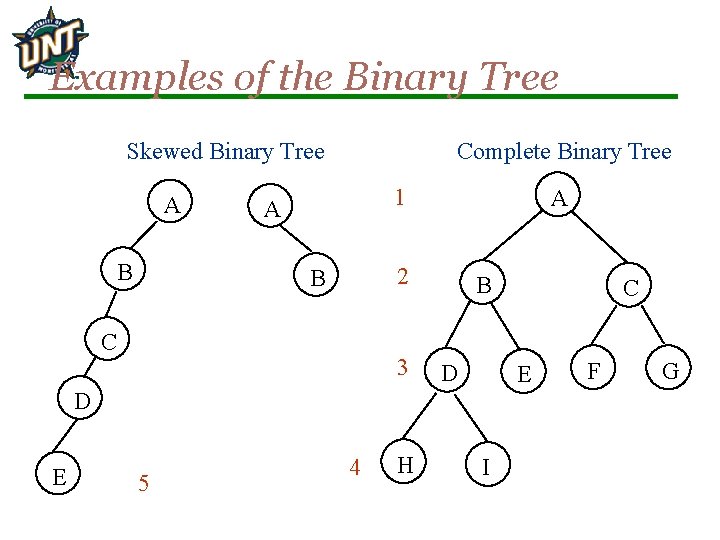
Examples of the Binary Tree Complete Binary Tree Skewed Binary Tree A B 1 A A 2 B C 3 B D E 5 4 H C I F G

Differences Between A Tree and A Binary Tree The subtrees of a binary tree are ordered; those of a tree are not ordered. A B • Are different when viewed as binary trees. • Are the same when viewed as trees.
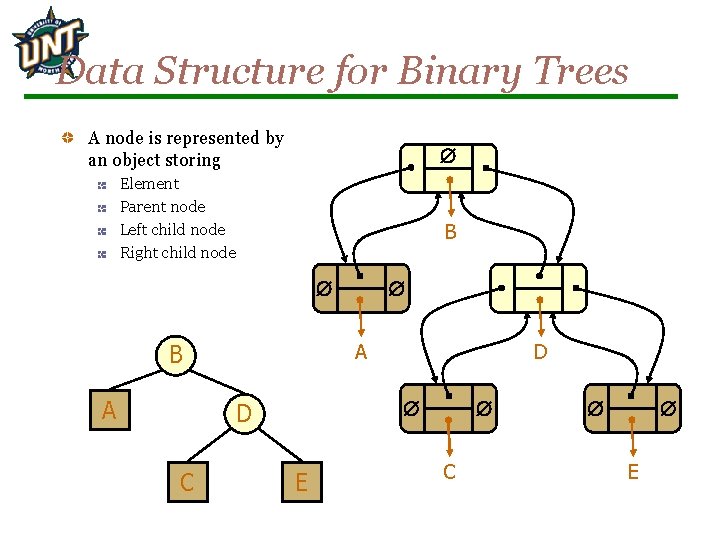
Data Structure for Binary Trees A node is represented by an object storing Element Parent node Left child node Right child node B B A A D D C E C E
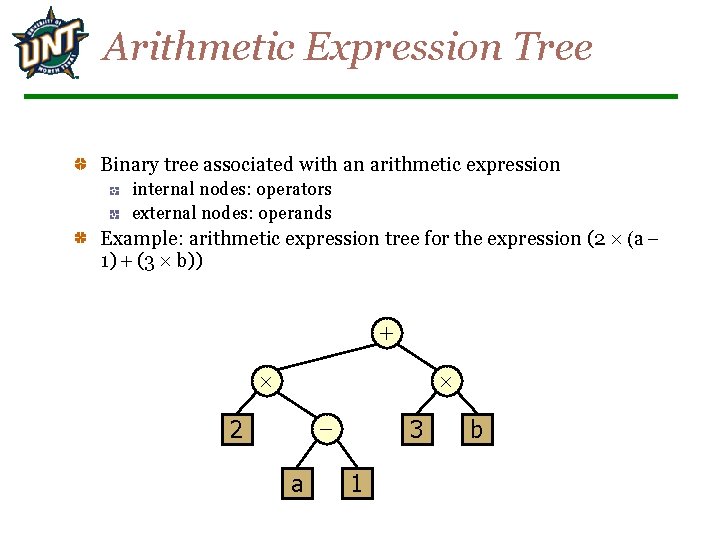
Arithmetic Expression Tree Binary tree associated with an arithmetic expression internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a 1) + (3 b)) + - 2 a 3 1 b
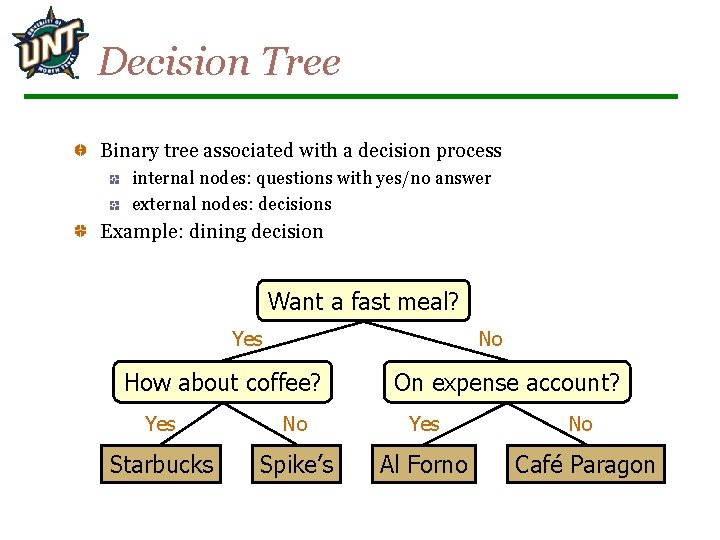
Decision Tree Binary tree associated with a decision process internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon

Maximum Number of Nodes in a Binary Tree The maximum number of nodes on depth i of a binary tree is 2 i, i>=0. The maximum nubmer of nodes in a binary tree of height k is 2 k+1 -1, k>=0. Prove by induction.
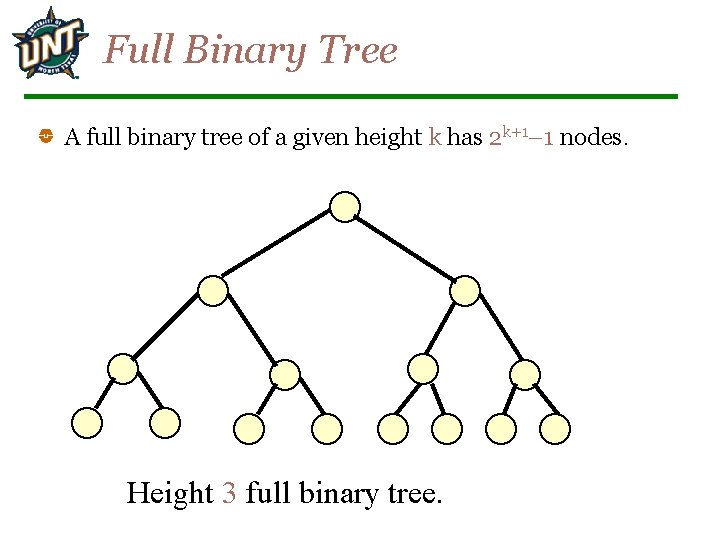
Full Binary Tree A full binary tree of a given height k has 2 k+1– 1 nodes. Height 3 full binary tree.
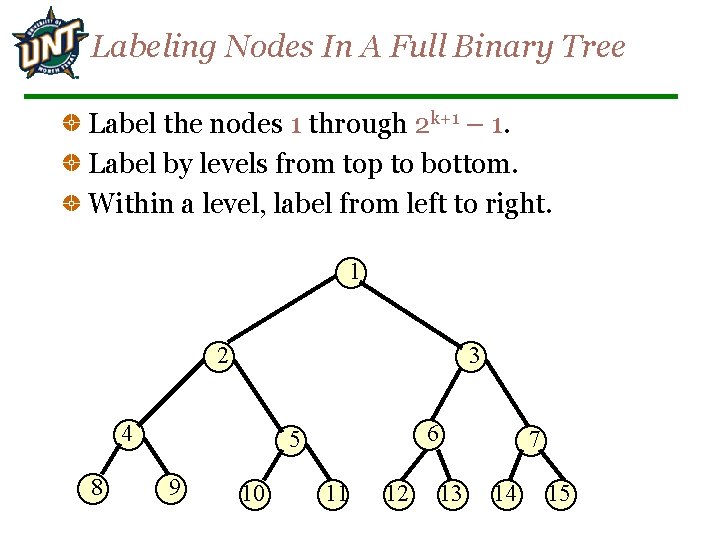
Labeling Nodes In A Full Binary Tree Label the nodes 1 through 2 k+1 – 1. Label by levels from top to bottom. Within a level, label from left to right. 1 2 3 4 8 6 5 9 10 11 12 7 13 14 15
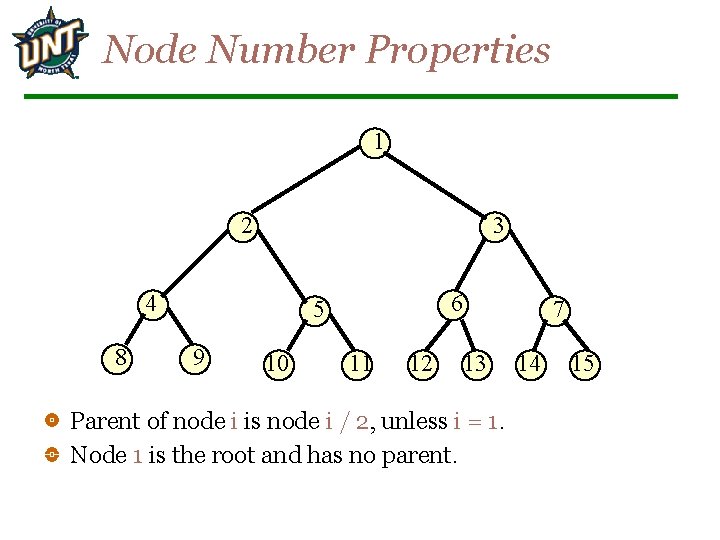
Node Number Properties 1 2 3 4 8 6 5 9 10 11 12 7 13 Parent of node i is node i / 2, unless i = 1. Node 1 is the root and has no parent. 14 15
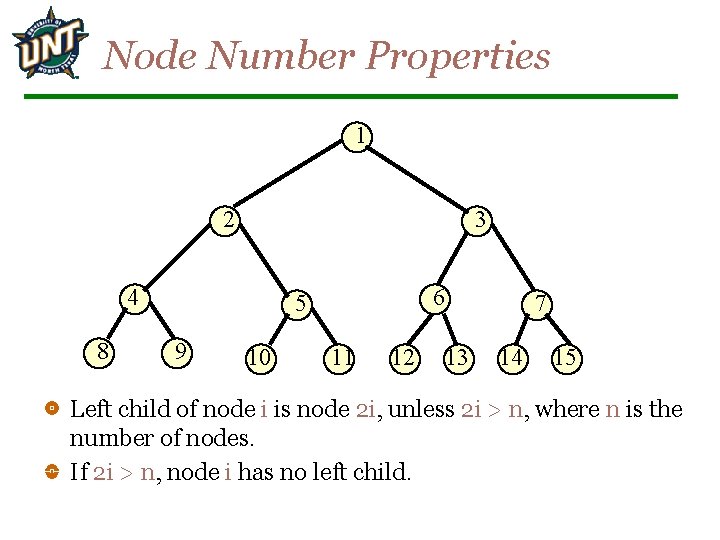
Node Number Properties 1 2 3 4 8 6 5 9 10 11 12 7 13 14 15 Left child of node i is node 2 i, unless 2 i > n, where n is the number of nodes. If 2 i > n, node i has no left child.
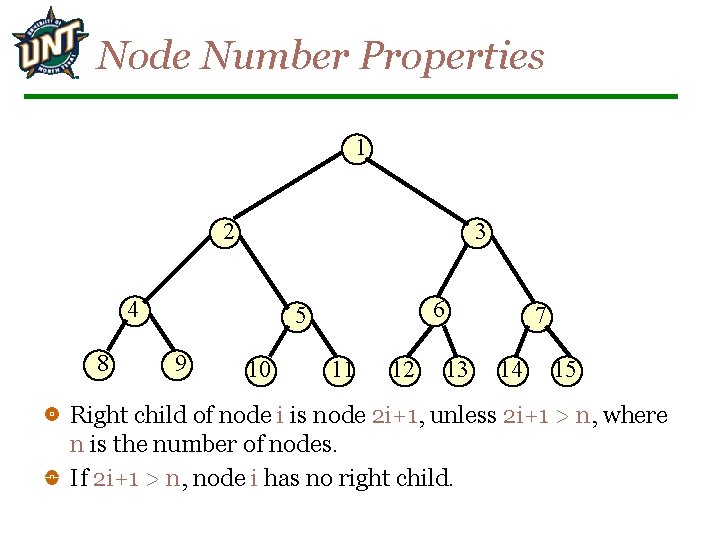
Node Number Properties 1 2 3 4 8 6 5 9 10 11 12 7 13 14 15 Right child of node i is node 2 i+1, unless 2 i+1 > n, where n is the number of nodes. If 2 i+1 > n, node i has no right child.
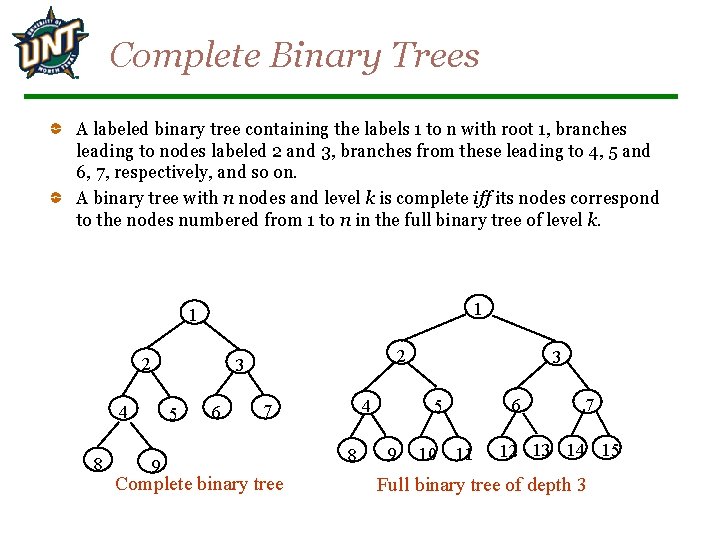
Complete Binary Trees A labeled binary tree containing the labels 1 to n with root 1, branches leading to nodes labeled 2 and 3, branches from these leading to 4, 5 and 6, 7, respectively, and so on. A binary tree with n nodes and level k is complete iff its nodes correspond to the nodes numbered from 1 to n in the full binary tree of level k. 1 1 2 4 8 2 3 5 9 6 Complete binary tree 8 6 5 4 7 3 9 10 11 7 12 13 14 15 Full binary tree of depth 3

Binary Tree Traversals Let l, R, and r stand for moving left, visiting the node, and moving right. There are six possible combinations of traversal l. Rr, lr. R, Rlr, Rrl, r. Rl, rl. R Adopt convention that we traverse left before right, only 3 traversals remain l. Rr, lr. R, Rlr inorder, postorder, preorder
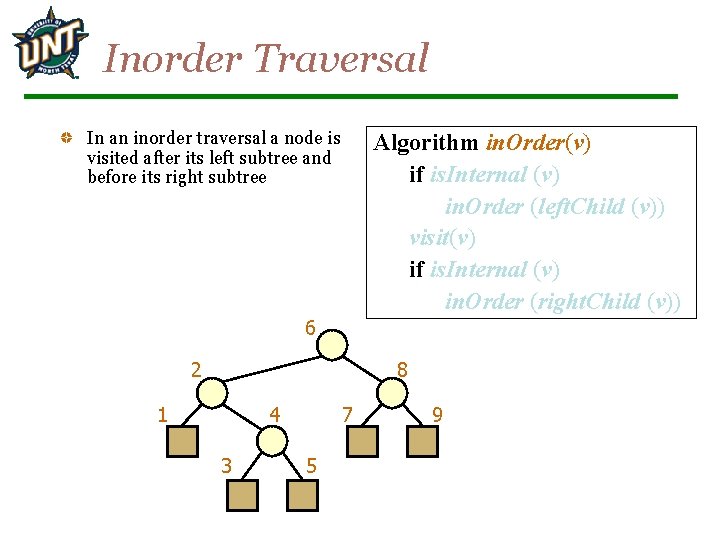
Inorder Traversal In an inorder traversal a node is visited after its left subtree and before its right subtree Algorithm in. Order(v) if is. Internal (v) in. Order (left. Child (v)) visit(v) if is. Internal (v) in. Order (right. Child (v)) 6 2 8 1 4 3 7 5 9
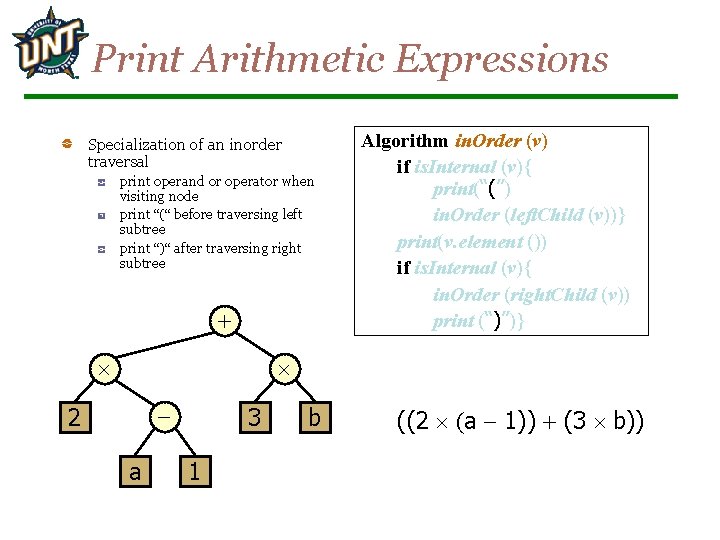
Print Arithmetic Expressions Specialization of an inorder traversal print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + Algorithm in. Order (v) if is. Internal (v){ print(“(’’) in. Order (left. Child (v))} print(v. element ()) if is. Internal (v){ in. Order (right. Child (v)) print (“)’’)} - 2 a 3 1 b ((2 (a - 1)) + (3 b))
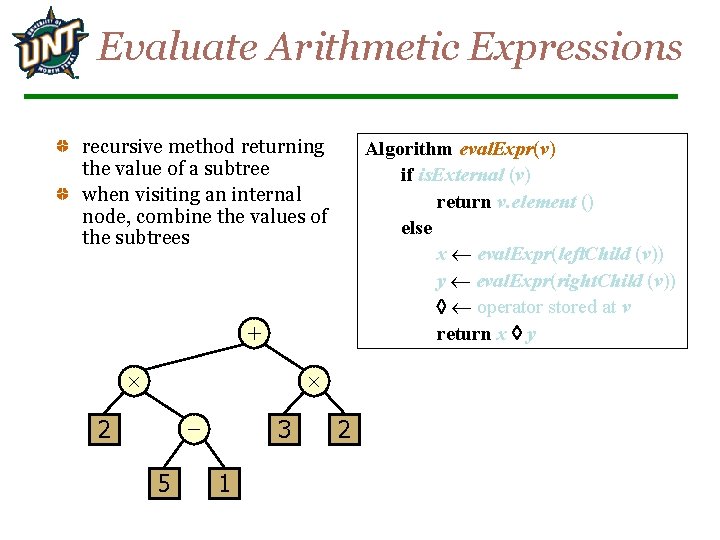
Evaluate Arithmetic Expressions recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left. Child (v)) y eval. Expr(right. Child (v)) operator stored at v return x y + - 2 5 3 1 2

Creativity: path. Length(tree) = depth(v) v tree Algorithm path. Length(v, n) Input: a tree node v and an initial value n Output: the path. Length of the tree with root v Usage: pl = path. Length(root, 0); if is. External (v) return n return (path. Length(left. Child (v), n + 1) + path. Length(right. Child (v), n + 1) + n)
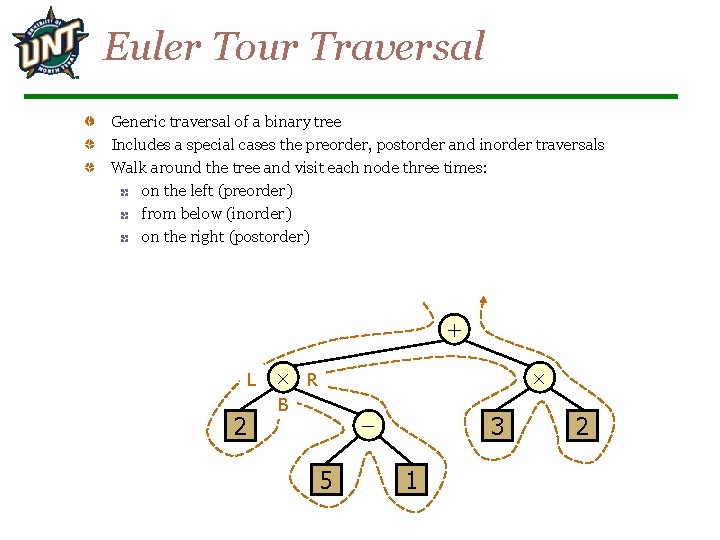
Euler Tour Traversal Generic traversal of a binary tree Includes a special cases the preorder, postorder and inorder traversals Walk around the tree and visit each node three times: on the left (preorder) from below (inorder) on the right (postorder) + L 2 R B 5 3 1 2

Euler Tour Traversal euler. Tour(node v) { perform action for visiting node on the left; if v is internal then euler. Tour(v->left); perform action for visiting node from below; if v is internal then euler. Tour(v->right); perform action for visiting node on the right; }
- Slides: 78