Trees A tree is a data structure used

Trees • A tree is a data structure used to represent different kinds of data and help solve a number of algorithmic problems • Game trees (i. e. , chess ), UNIX directory trees, sorting trees etc • We will study extensively two useful kind of trees: Binary Search Trees and Heaps 1

Trees: Definitions • Trees have nodes. They also have edges that connect the nodes. Between two nodes there is always only one path. Tree nodes Tree edges 2

Trees: More Definitions • Trees are rooted. Once the root is defined (by the user) all nodes have a specific level. • Trees have internal nodes and leaves. Every node (except the root) has a parent and it also has zero or more children. root level 0 level 1 internal nodes level 2 level 3 leaves parent and child 3

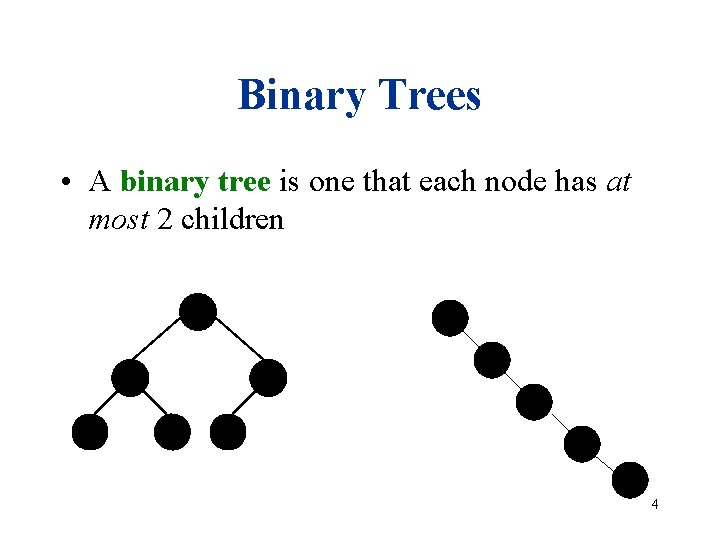
Binary Trees • A binary tree is one that each node has at most 2 children 4

Binary Trees: Definitions • Nodes in trees can contain keys (letters, numbers, etc) • Complete binary tree: the one where leaves are only in last two bottom levels with bottom one placed as far left as possible 14 10 8 7 16 12 9 11 13 15 18 5

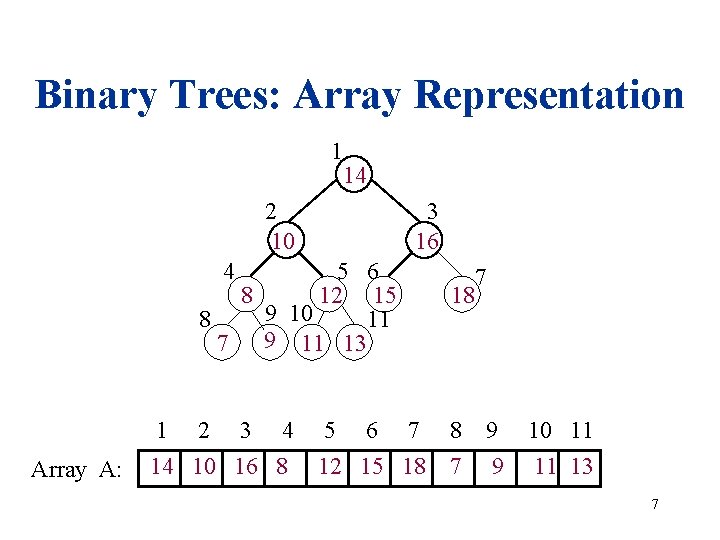
Binary Trees: Array Representation • Complete Binary Trees can be represented in memory with the use of an array A so that all nodes can be accessed in O(1) time: – Label nodes sequentially top-to-bottom and leftto-right – Left child of A[i] is at position A[2 i] – Right child of A[i] is at position A[2 i + 1] – Parent of A[i] is at A[i/2] 6

Binary Trees: Array Representation 1 14 2 10 3 16 4 5 6 8 12 15 9 10 8 11 7 9 11 13 Array A: 1 2 3 4 14 10 16 8 5 6 7 12 15 18 18 8 7 7 9 9 10 11 11 13 7

Binary Trees: Pointer Representation • To freely move up and down the tree we need pointers to parent (NIL for root) and pointers to children (NIL for leaves) typedef tree_node { int key; struct tree_node *parent; struct tree_node *left, *right; } 8

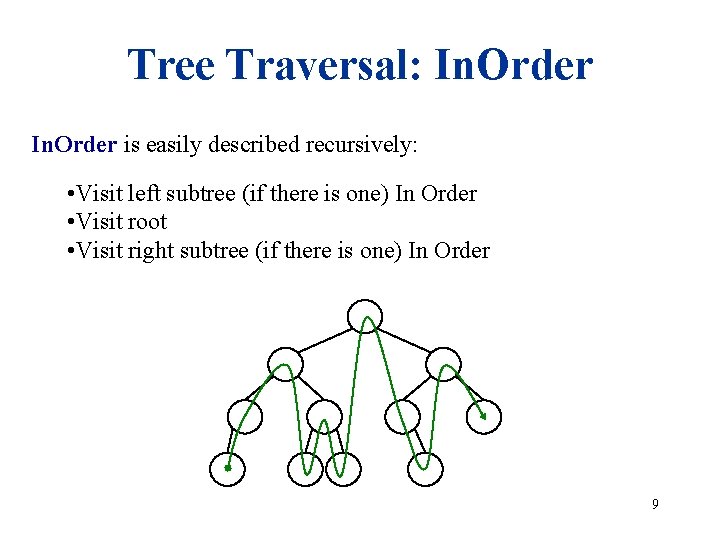
Tree Traversal: In. Order is easily described recursively: • Visit left subtree (if there is one) In Order • Visit root • Visit right subtree (if there is one) In Order 9

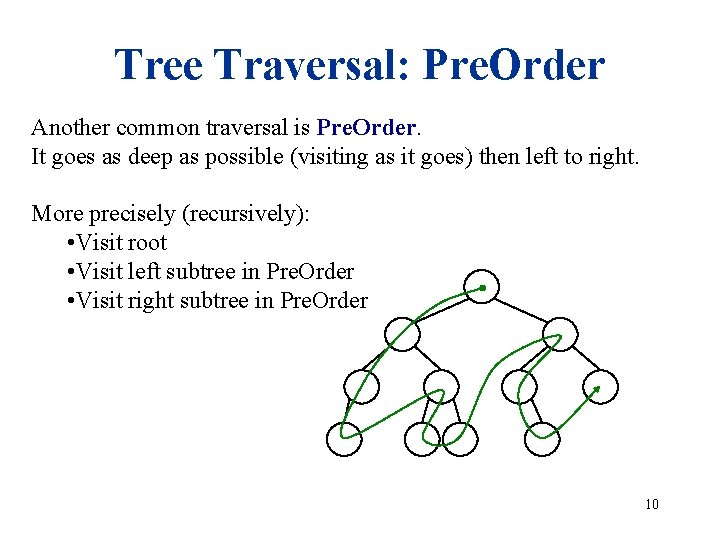
Tree Traversal: Pre. Order Another common traversal is Pre. Order. It goes as deep as possible (visiting as it goes) then left to right. More precisely (recursively): • Visit root • Visit left subtree in Pre. Order • Visit right subtree in Pre. Order 10

Tree Traversal: Non-recursive Pre. Order can also be implemented with a stack, without recursion: Stack S push root onto S repeat until S is empty v = pop S if v is not NULL visit v push v’s right child onto S push v’s left child onto S 11

Tree Traversal: Post. Order traversal also goes as deep as possible, but only visits internal nodes during backtracking. More precisely (recursive): • Visit left subtree in Post. Order • Visit right subtree in Post. Order • Visit root 12

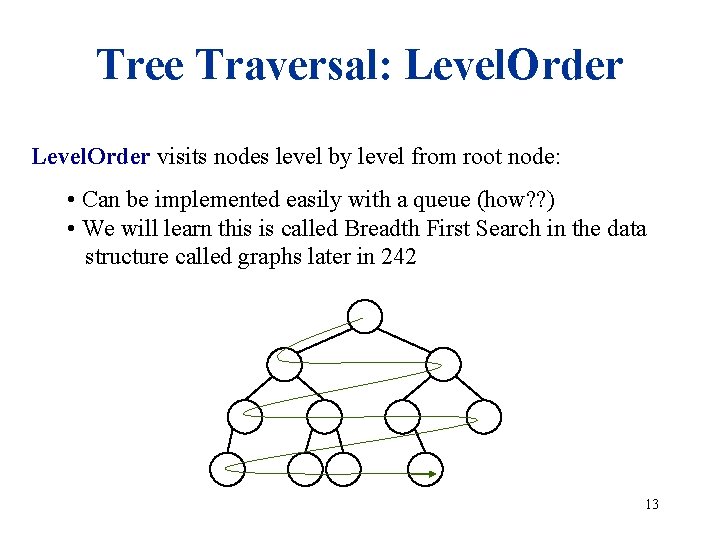
Tree Traversal: Level. Order visits nodes level by level from root node: • Can be implemented easily with a queue (how? ? ) • We will learn this is called Breadth First Search in the data structure called graphs later in 242 13

Binary Search Trees • A Binary Search Tree (BST) is a binary tree with the following properties: – The key of a node is always greater than the keys of the nodes in its left subtree – The key of a node is always smaller than the keys of the nodes in its right subtree 14

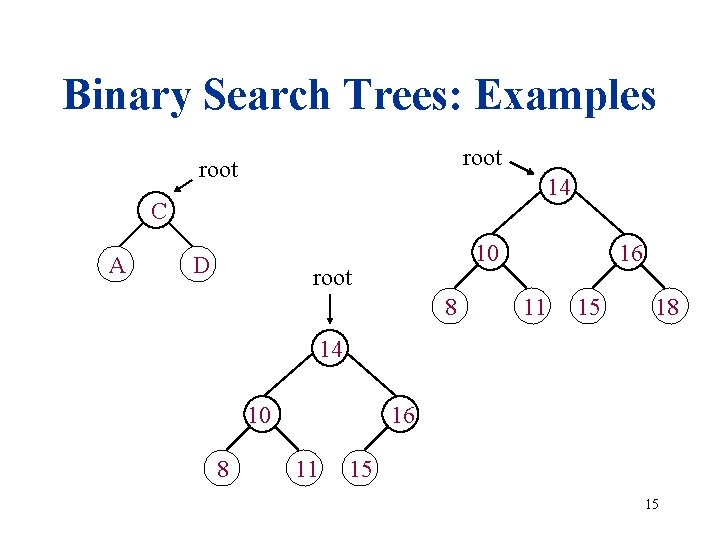
Binary Search Trees: Examples root 14 C A D 10 root 8 16 11 15 18 14 10 8 16 11 15 15

Binary Search Trees • BST is a tree with the following BST property: key. left < key. parent < key. right NOTE! When nodes of a BST are traversed by Inorder traversal the keys appear in sorted order: inorder(root) { inorder(root. left) print(root. key) inorder(root. right) } 16

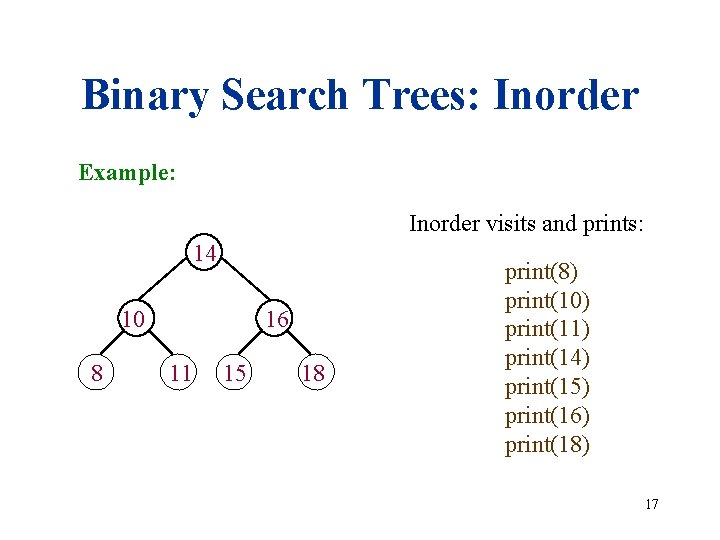
Binary Search Trees: Inorder Example: Inorder visits and prints: 14 10 8 16 11 15 18 print(8) print(10) print(11) print(14) print(15) print(16) print(18) 17

Searching for a key in a BST Picture BST’s Parent and Left/Right subtrees as follows: P L R Problem: how do you search BST for node with key x ? 18

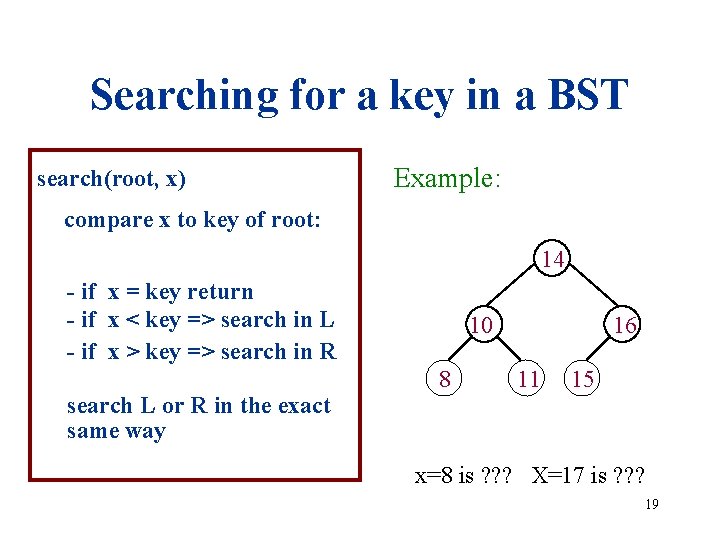
Searching for a key in a BST search(root, x) Example: compare x to key of root: 14 - if x = key return - if x < key => search in L - if x > key => search in R 10 8 16 11 15 search L or R in the exact same way x=8 is ? ? ? X=17 is ? ? ? 19

Searching for a key in a BST search. BST(root, key) /* found init to false */ if root=nil return if root. key=key then found=true return root else if key < root. key then search. BST(root. L, key) else search. BST(root. R, key) How can you rewrite search. BST non-recursively? 20

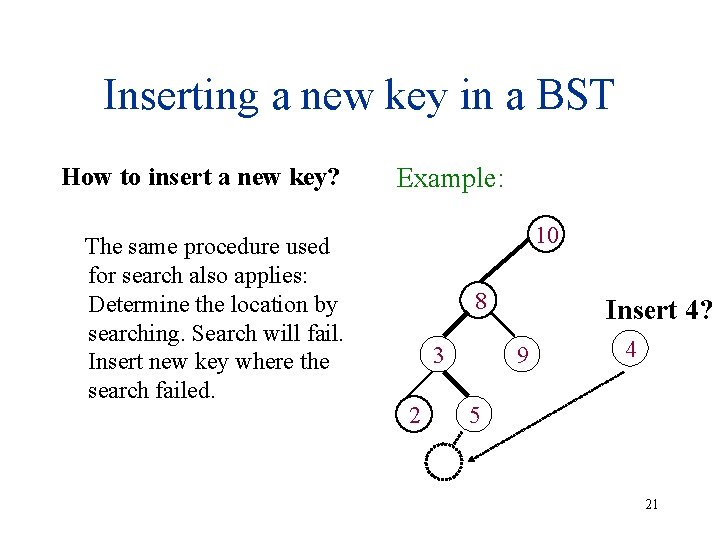
Inserting a new key in a BST How to insert a new key? The same procedure used for search also applies: Determine the location by searching. Search will fail. Insert new key where the search failed. Example: 10 8 3 2 Insert 4? 9 4 5 21

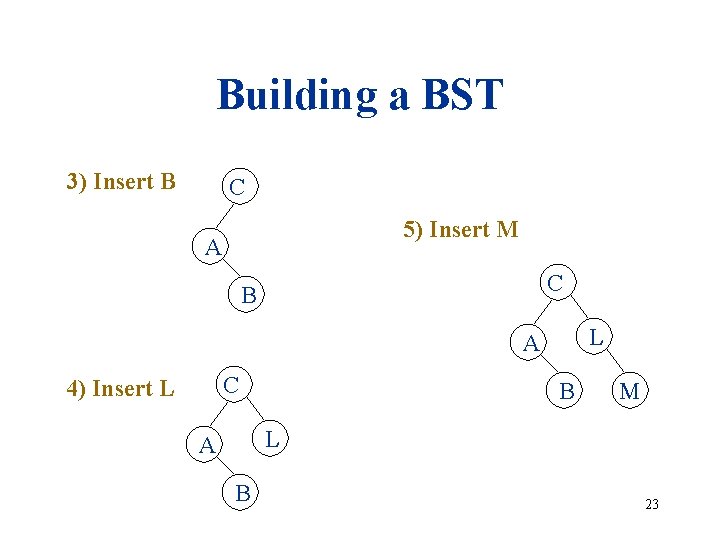
Building a BST Build a BST from a sequence of nodes read one a time Example: Inserting 1) Insert C C A B L M (in this order!) 2) Insert A C C A 22

Building a BST 3) Insert B C 5) Insert M A C B L A C 4) Insert L B M L A B 23

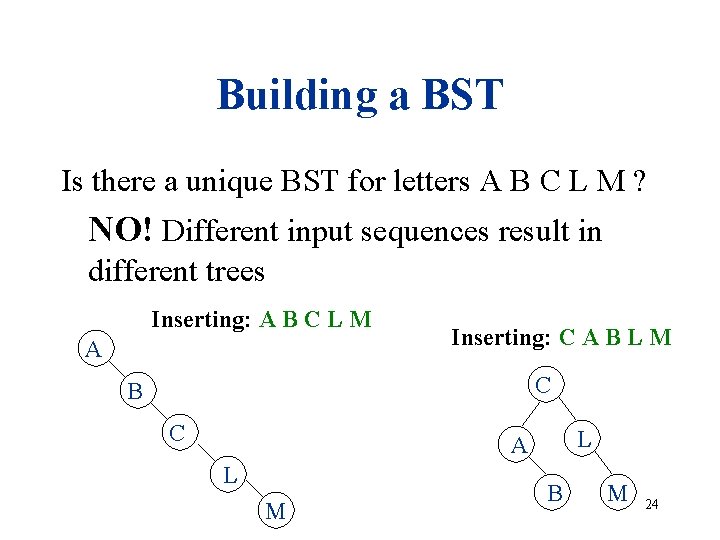
Building a BST Is there a unique BST for letters A B C L M ? NO! Different input sequences result in different trees Inserting: A B C L M A Inserting: C A B L M C B C L A L M B M 24

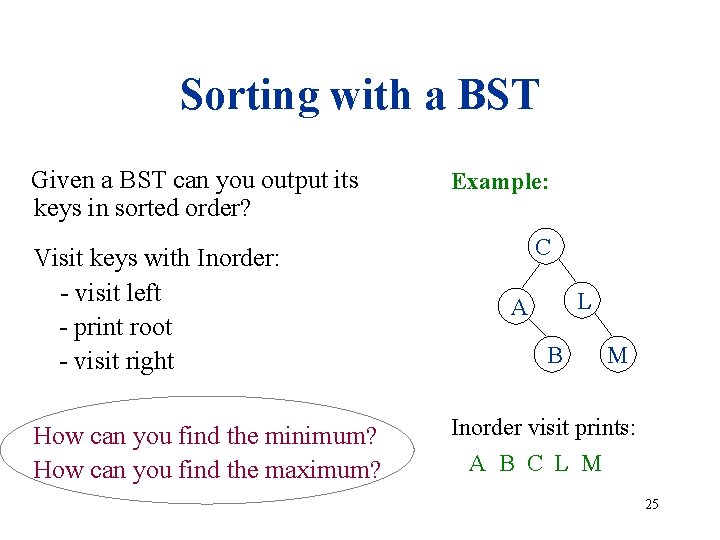
Sorting with a BST Given a BST can you output its keys in sorted order? Visit keys with Inorder: - visit left - print root - visit right How can you find the minimum? How can you find the maximum? Example: C L A B M Inorder visit prints: A B C L M 25

Deleting from a BST To delete node with key x first you need to search for it. Once found, apply one of the following three cases CASE A: x is a leaf p p q r x delete x BST property maintained 26

Deleting from a BST cont. Case B: x is interior with only one subtree r r x q L q delete x L BST property maintained 27

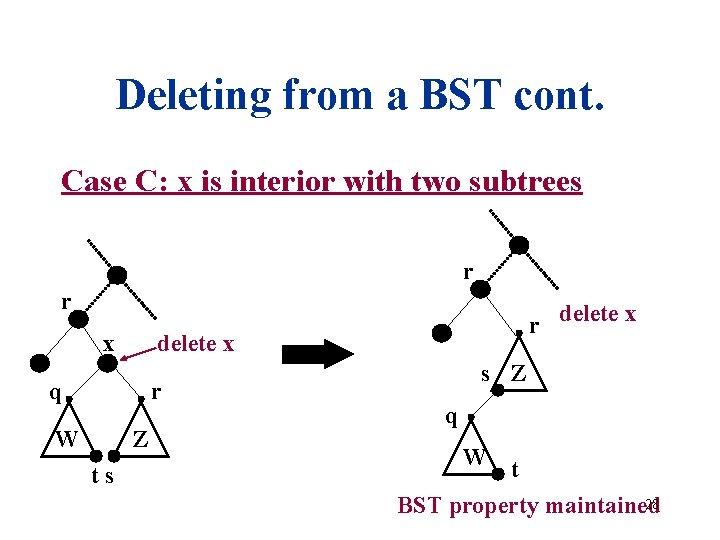
Deleting from a BST cont. Case C: x is interior with two subtrees r r x delete x q r W Z ts r delete x s Z q W t 28 BST property maintained

Deleting from a BST cont. Case C cont: … or you can also do it like this q < x < r r Þ Q is smaller than the smaller element in Z Þ R is larger than the largest element in W q W t r s Z Can you see other possible ways ? 29

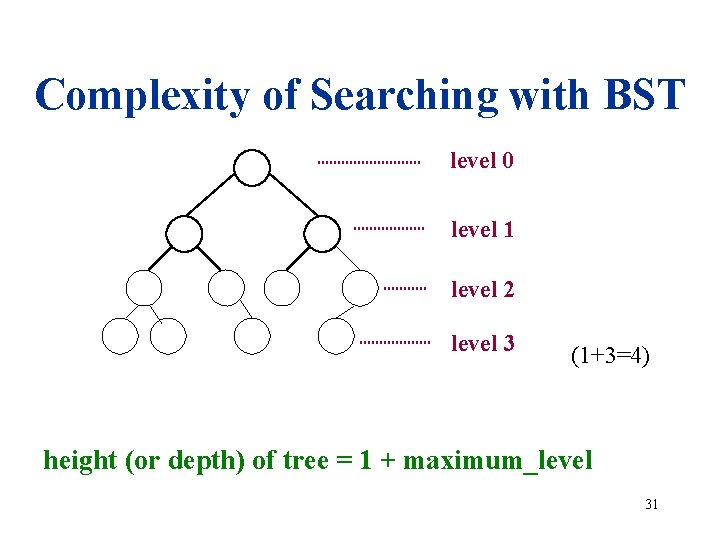
Complexity of Searching with BST • What is the complexity of search. BST ? • It depends on: – the key x – The other data – The shape of the tree (full, arbitrary) Complexity Analysis: We are interested in best case, worst case and average case 30

Complexity of Searching with BST level 0 level 1 level 2 level 3 (1+3=4) height (or depth) of tree = 1 + maximum_level 31

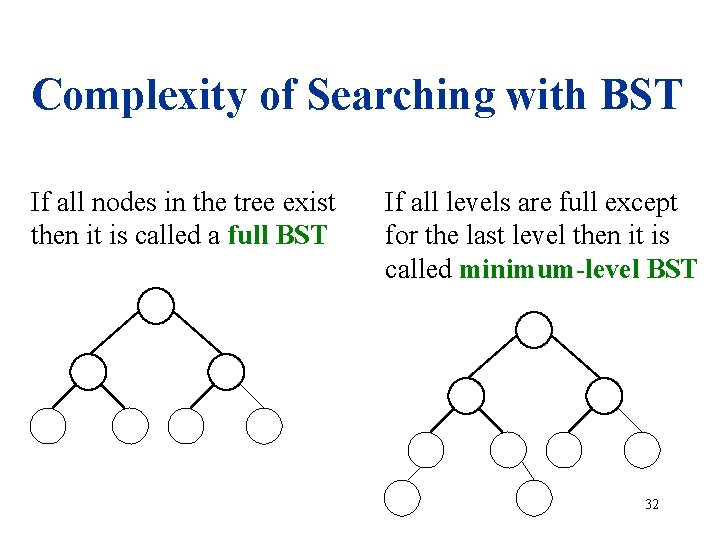
Complexity of Searching with BST If all nodes in the tree exist then it is called a full BST If all levels are full except for the last level then it is called minimum-level BST 32

Complexity of Searching with BST h Theorem: A full BST of height h has 2 - 1 nodes Proof: Use induction Inductive Basis: A tree of height 1 has one node (root) Inductive Hypothesis: Assume that a tree of height h has h 2 - 1 nodes 33

Complexity of Searching with BST Inductive step: Connect two trees of height h to make one of height h+1. You need to add one more node for the new root h+1 L R h By inductive hypothesis the new number of nodes is h h (2 - 1) + (2 -1) + 1 = 2 h+1 -1 ……proved! 34

Complexity of Searching with BST Theorem: For a minimum level tree of height h: 2 h-1 h - 1 < # of nodes < 2 - 1 Corollary: The tree with the smallest height with n # of nodes it has a height of h n = 1 + log n 2 WHY? 35

Complexity of Searching with BST Therefore, for a full BST with N nodes the following holds for search. BST: best time analysis ………… O(1) worst time analysis ………… O(log N) average case analysis ………… ? ? ? We need to find what the average is!! 36

Complexity of Searching with BST • To define what average means you need to: – Find out all possibilities and … – Determine the probability of each possibility … – that is, you need to find the expected value: Possible values for the number of steps j are 1, 2, …, h as we assume that key search value is equally to occur 37