Trees A Quick Introduction to Graphs Definition of

Trees • • • A Quick Introduction to Graphs Definition of Trees Rooted Trees Binary Search Trees CS 103 1

Introduction to Graphs • A graph is a finite set of nodes with edges between nodes • Formally, a graph G is a structure (V, E) consisting of – a finite set V called the set of nodes, and – a set E that is a subset of Vx. V. That is, E is a set of pairs of the form (x, y) where x and y are nodes in V CS 103 2

Examples of Graphs • V={1, 2, 3, 4, 5} • E={(1, 2), (2, 3), (2, 4), (4, 2), (3, 3), (5, 4)} 2 1 3 5 When (x, y) is an edge, we say that x is adjacent to y. 1 is adjacent to 2. 2 is not adjacent to 1. 4 is not adjacent to 3. 4 CS 103 3

A “Real-life” Example of a Graph • V=set of 6 people: John, Mary, Joe, Helen, Tom, and Paul, of ages 12, 15, 13, and 13, respectively. • E ={(x, y) | if x is younger than y} Mary Helen Joe John Tom Paul CS 103 4

Intuition Behind Graphs • The nodes represent entities (such as people, cities, computers, words, etc. ) • Edges (x, y) represent relationships between entities x and y, such as: – – – “x loves y” “x hates y” “x is as smart as y” “x is a sibling of y” “x is bigger than y” ‘x is faster than y”, … CS 103 5

Directed vs. Undirected Graphs • If the directions of the edges matter, then we show the edge directions, and the graph is called a directed graph (or a digraph) • The previous two examples are digraphs • If the relationships represented by the edges are symmetric (such as (x, y) is edge if and only if x is a sibling of y), then we don’t show the directions of the edges, and the graph is called an undirected graph. CS 103 6

Examples of Undirected Graphs • V=set of 6 people: John, Mary, Joe, Helen, Tom, and Paul, where the first 4 are siblings, and the last two are siblings • E ={(x, y) | x and y are siblings} Mary Helen Joe John Tom Paul CS 103 7

Definition of Some Graph Related Concepts (Paths) • A path in a graph G is a sequence of nodes x 1, x 2, …, xk, such that there is an edge from each node the next one in the sequence • For example, in the first example graph, the sequence 4, 1, 2, 3 is a path, but the sequence 1, 4, 5 is not a path because (1, 4) is not an edge • In the “sibling-of” graph, the sequence John, Mary, Joe, Helen is a path, but the sequence Helen, Tom, Paul is not a path CS 103 8

Definition of Some Graph Related Concepts (Cycles) • A cycle in a graph G is a path where the last node is the same as the first node. • In the “sibling-of” graph, the sequence John, Mary, Joe, Helen, John is a cycle, but the sequence Helen, Tom, Paul, Helen is not a cycle CS 103 9

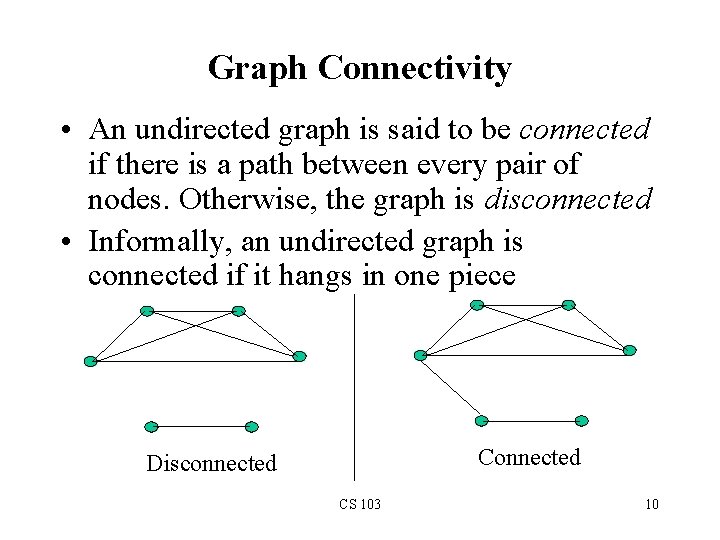
Graph Connectivity • An undirected graph is said to be connected if there is a path between every pair of nodes. Otherwise, the graph is disconnected • Informally, an undirected graph is connected if it hangs in one piece Connected Disconnected CS 103 10

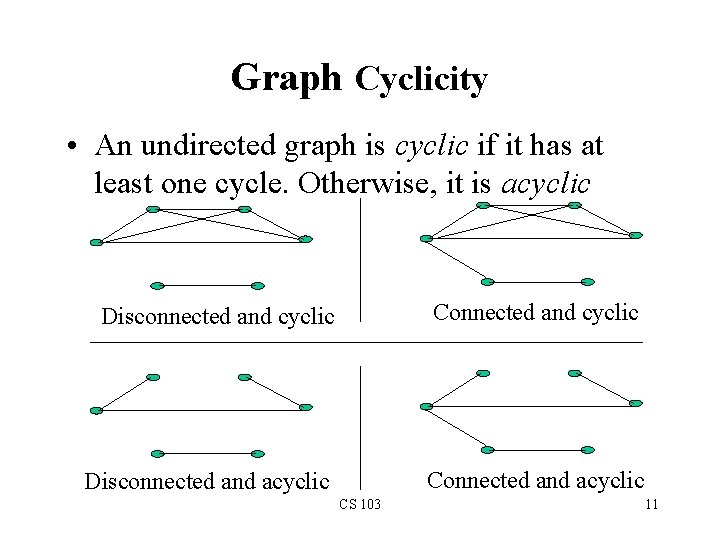
Graph Cyclicity • An undirected graph is cyclic if it has at least one cycle. Otherwise, it is acyclic Disconnected and cyclic Connected and cyclic Disconnected and acyclic CS 103 11

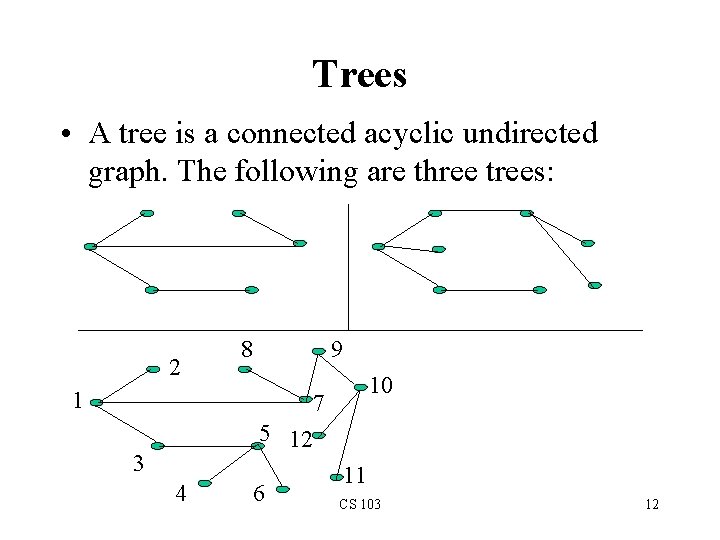
Trees • A tree is a connected acyclic undirected graph. The following are three trees: 2 1 8 9 10 7 5 12 3 4 6 11 CS 103 12

Rooted Trees • • A rooted tree is a tree where one of the nodes is designated as the root node. (Only one root in a tree) A rooted tree has a hierarchical structure: the root on top, followed by the nodes adjacent to it right below, followed by the nodes adjacent to those next, and so on. CS 103 13

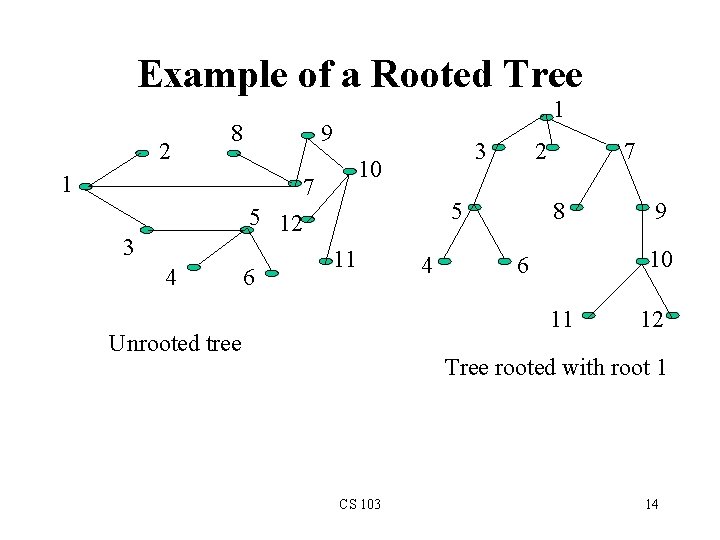
Example of a Rooted Tree 2 8 1 1 9 10 7 5 12 3 4 6 3 2 5 11 4 7 8 10 6 11 Unrooted tree 9 12 Tree rooted with root 1 CS 103 14

Tree-Related Concepts • The nodes adjacent to x and below x are called the children of x, 1 and x is called their parents 3 2 7 • A node that has no children is called a leaf 5 8 9 • The descendents of a node 10 4 6 are: itself, its children, 11 12 their children, all the way down • The ancestors of a node are: itself, its parent, its grandparent, all the way to the root CS 103 15

Tree-Related Concepts (Contd. ) • The depth of a node is the number of edges 1 from the root to that node. 3 2 7 • The depth (or height) of a rooted tree is the depth 5 8 9 of the lowest leaf 10 4 6 • Depth of node 10: 3 11 12 • Depth of this tree: 4 CS 103 16

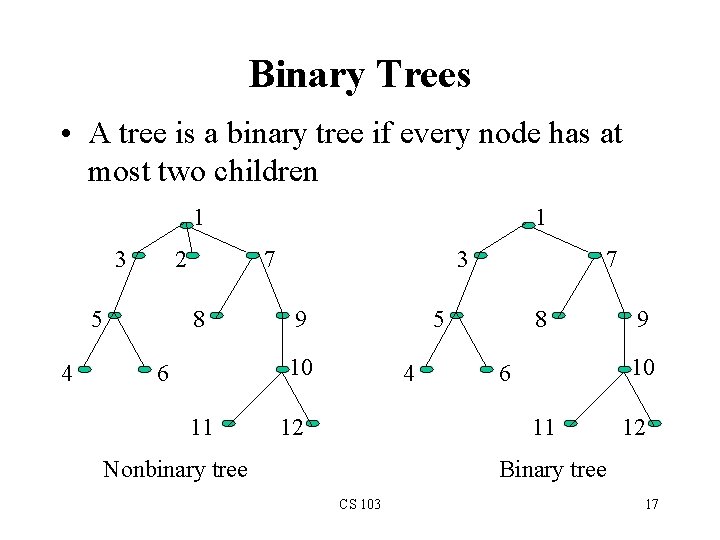
Binary Trees • A tree is a binary tree if every node has at most two children 1 3 2 5 4 1 7 8 3 9 5 10 6 11 7 4 12 8 10 6 11 Nonbinary tree 9 12 Binary tree CS 103 17

Binary-Tree Related Definitions • The children of any node in a binary tree are ordered into a left child and a right child 1 • A node can have a left and 3 a right child, a left child only, a right child only, 5 8 or no children 4 6 • The tree made up of a left child (of a node x) and all its 11 descendents is called the left subtree of x • Right subtrees are defined similarly CS 103 7 9 10 12 18

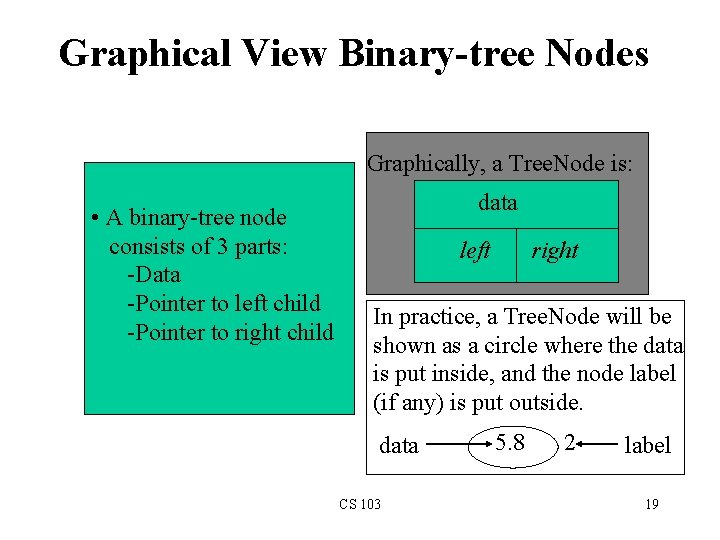
Graphical View Binary-tree Nodes Graphically, a Tree. Node is: • A binary-tree node consists of 3 parts: -Data -Pointer to left child -Pointer to right child data left right In practice, a Tree. Node will be shown as a circle where the data is put inside, and the node label (if any) is put outside. data CS 103 5. 8 2 label 19

A Binary-tree Node Class class Tree. Node { public: typedef int datatype; Tree. Node(datatype x=0, Tree. Node *left=NULL, Tree. Node *right=NULL){ data=x; this->left=left; this->right=right; }; datatype get. Data( ) {return data; }; Tree. Node *get. Left( ) {return left; }; Tree. Node *get. Right( ) {return right; }; void set. Data(datatype x) {data=x; }; void set. Left(Tree. Node *ptr) {left=ptr; }; void set. Right(Tree. Node *ptr) {right=ptr; }; private: datatype data; // different data type for other apps Tree. Node *left; // the pointer to left child Tree. Node *right; // the pointer to right child }; CS 103 20

Binary Tree Class class Tree { public: typedef int datatype; Tree(Tree. Node *root. Ptr=NULL){this->root. Ptr=root. Ptr; }; Tree. Node *search(datatype x); bool insert(datatype x); Tree. Node * remove(datatype x); Tree. Node *get. Root(){return root. Ptr; }; Tree *get. Left. Subtree(); Tree *get. Right. Subtree(); bool is. Empty(){return root. Ptr == NULL; }; private: Tree. Node *root. Ptr; }; CS 103 21

Binary Search Trees • A binary search tree (BST) is a binary tree where – Every node holds a data value (called key) – For any node x, all the keys in the left subtree of x are ≤ the key of x – For any node x, all the keys in the right subtree of x are > the key of x CS 103 22

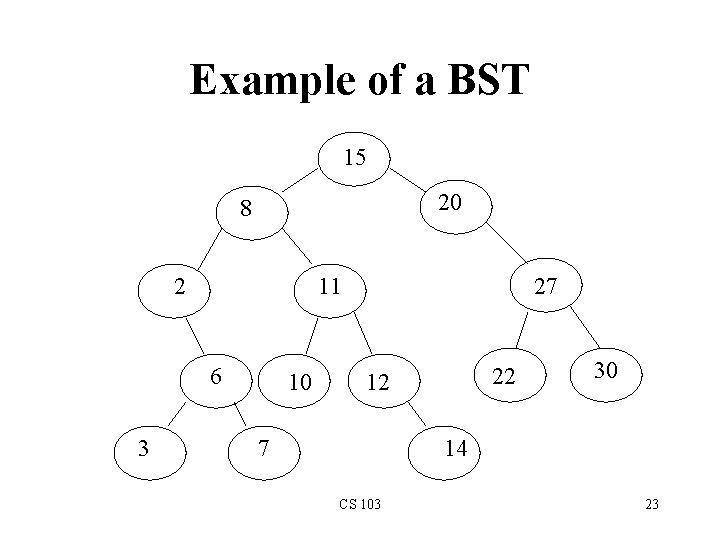
Example of a BST 15 20 8 2 11 6 3 10 27 22 12 7 30 14 CS 103 23

Searching in a BST 15 • To search for a number b: 1. Compare b with the root; – – – If b=root, return If b<root, go left If b>root, go right 20 8 6 10 12 3 27 11 2 7 22 30 14 2. Repeat step 1, comparing b with the new node we are at. 3. Repeat until either the node is found or we reach a non-existing node • Try it with b=12, and also with b=17 CS 103 24

Code for Search in BST // returns a pointer to the Tree. Node that contains x, // if one is found. Otherwise, it returns NULL Tree. Node * Tree: : search(datatype x){ if (is. Empty()) {return NULL; } Tree. Node *p=root. Ptr; while (p != NULL){ datatype a = p->get. Data(); if (a == x) return p; else if (x<a) p=p->get. Left(); else p=p->get. Right(); } return NULL; }; CS 103 25

Insertion into a BST Insert(datatype b, Tree T): 1. Search for the position of b as if it were in the tree. The position is the left or right child of some node x. 2. Create a new node, and assign its address to the appropriate pointer field in x 3. Assign b to the data field of the new node CS 103 26

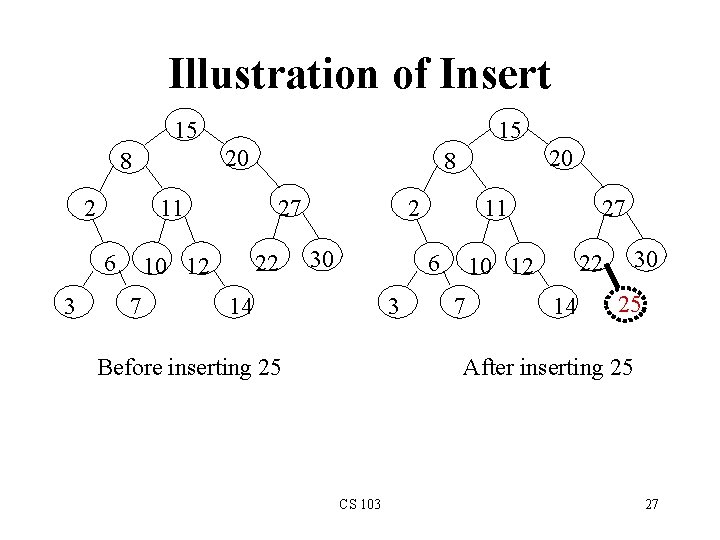
Illustration of Insert 15 20 8 2 11 6 3 15 27 22 10 12 7 20 8 2 30 11 6 3 14 Before inserting 25 27 7 30 22 10 12 14 25 After inserting 25 CS 103 27

Code for Insert in BST bool Tree: : insert(datatype x){ if (is. Empty()) {root. Ptr = new Tree. Node(x); return true; } Tree. Node *p=root. Ptr; while (p != NULL){ datatype a = p->get. Data(); if (a == x) return false; // data is already there else if (x<a){ if (p->get. Left() == NULL){ // place to insert Tree. Node *new. Node. Ptr= new Tree. Node(x); p->set. Left(new. Node. Ptr); return true; } else p=p->get. Left(); }else { // a>a if (p->get. Right() == NULL){ // place to insert Tree. Node *new. Node. Ptr= new Tree. Node(x); p->set. Right(new. Node. Ptr); return true; } else p=p->get. Right(); } } }; CS 103 28

Deletion from a BST • Illustration in class CS 103 29

Deletion from a BST (pseudocode) Delete(datatype b, Tree T) 1. Search for b in tree T. If not found, return. 2. Call x the first node found to contain b 3. If x is a leaf, remove x and set the appropriate pointer in the parent of x to NULL 4. If x has only one child y, remove x, and the parent of x become a direct parent of y (More on the next slide) CS 103 30

Deletion (contd. ) 5. If x has two children, go to the left subtree, and find there in largest node, and call it y. The node y can be found by tracing the rightmost path until the end. Note that y is either a leaf or has no right child 6. Copy the data field of y onto the data field of x 7. Now delete node y in a manner similar to step 4. CS 103 31

Code for Delete in BST(4 slides) // finds x in the tree, removes it, and returns a pointer to the containing // Tree. Node. If x is not found, the function returns NULL. Tree. Node * Tree: : remove(datatype x){ if (is. Empty()) return NULL; Tree. Node *p=root. Ptr; Tree. Node *parent = NULL; // parent of p char what. Child; // 'L' if p is a left child, 'R' O. W. while (p != NULL){ datatype a = p->get. Data(); if (a == x) break; // x found else if(x<a) { parent = p; what. Child = 'L'; p=p->get. Left(); } else {parent = p; what. Child = 'R'; p=p->get. Right(); } } if (p==NULL) return NULL; // x was not found CS 103 32

// Handle the case where p is a leaf. // Turn the appropriate pointer in its parent to NULL if (p->get. Left() == NULL && p->get. Right() == NULL){ if (parent != NULL) // x is not at the root if (what. Child == 'L') parent->set. Left(NULL); else parent->set. Right(NULL); else // x is at the root. Ptr=NULL; return p; } CS 103 33

else if (p->get. Left() == NULL){ // p has only one a child -- a right child. Let the parent of p // become an immediate parent of the right child of p. if (parent != NULL) // p is not the root if (what. Child == 'L') parent->set. Left(p->get. Right()); else parent->set. Right(p->get. Right()); else root. Ptr=p->get. Right(); // p is the root return p; } else if (p->get. Right() == NULL){ // p has only one a child -- a left child. Let the parent of p // become an immediate parent of the left child of p. if (parent != NULL) // p is not the root if (what. Child == 'L') parent->set. Left(p->get. Left()); else parent->set. Right(p->get. Left()); else root. Ptr=p->get. Left(); // p is the root return p; } CS 103 34

else { // p has two children Tree. Node *return. Node= new Tree. Node(*p); // replicates p Tree. Node * left. Child = p->get. Left(); if (left. Child->get. Right() == NULL){// left. Child has no right child p->set. Data(left. Child->get. Data()); p->set. Left(left. Child->get. Left()); delete left. Child; return. Node; } Tree. Node * max. Left = left. Child->get. Right(); Tree. Node * parent 2 = left. Child; while (max. Left != NULL){parent 2 = max. Left; max. Left = max. Left ->get. Right(); } // now max. Left is the node to swap with p. p->set. Data(max. Left->get. Data()); if (max. Left->get. Left()==NULL) parent 2 ->set. Right(NULL); // max. Left a leaf else parent 2 ->set. Right(max. Left->get. Left()); //max. Left not a leaf delete max. Left; return. Node; } }; CS 103 35

Additional Things for YOU to Do • Add a method to the Tree class for returning the maximum value in the BST • Add a method to the Tree class for returning the minimum value in the BST • Write a function that takes as input an array of type datatype, and an integer n representing the length of the array, and returns a BST Tree Object containing the elements of the input array CS 103 36