Trees 3 The Binary Search Tree Section 4

Trees 3: The Binary Search Tree • Section 4. 3 1

Binary Search Tree • A binary tree B is called a binary search tree iff: – There is an order relation < defined for the vertices of B – For any vertex v, and any descendant u in the subtree v. left, u<v – For any vertex v, and any descendent w in the subtree v. right, v<w root 1 4 2 6 3 5 7 2
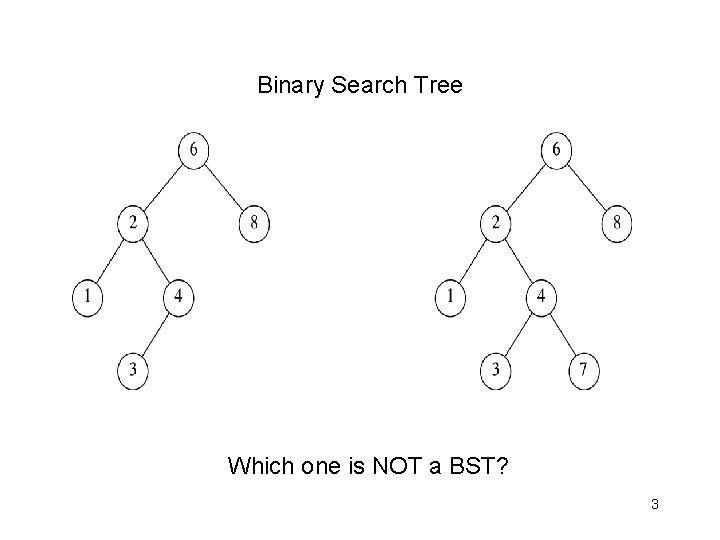
Binary Search Tree Which one is NOT a BST? 3

Binary Search Tree • Consequences – The smallest element in a binary search tree (BST) is the “left-most” node – The largest element in a BST is the “right-most” node – Inorder traversal of a BST encounters nodes in increasing order root 1 4 2 6 3 5 7 4

Binary Search using BST • Assumes nodes are organized in a binary search tree – Begin at root node – Descend using comparison to make left/right decision • if (search_value < node_value) go to the left child • else if (search_value > node_value) go to the right child • else return true (success) – Until descending move is impossible – Return false (failure) 5

Binary Search using BST • Runtime <= descending path length <= depth of tree • If tree has “enough” branching, runtime is O(log n) – Worst case is O(n) 6

BST Class Template 7

BST Class Template (contd. ) Pointer passed by reference (why? ) Internal functions used in recursive calls 8

BST: Public members calling private recursive functions 9

BST: Searching for an element 10

BST: Find the smallest element Tail recursion 11

BST: Find the biggest element Non-recursive 12
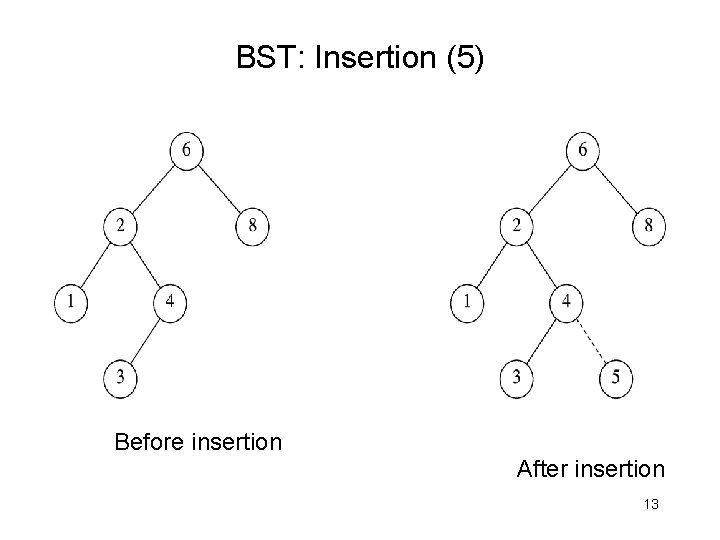
BST: Insertion (5) Before insertion After insertion 13

BST: Insertion (contd. ) Strategy: • Traverse the tree as in searching for t with contains() • Insert if you cannot find t 14
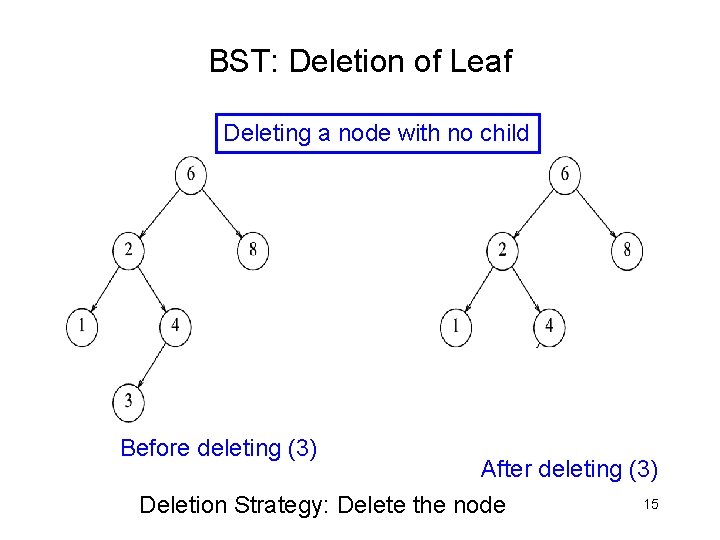
BST: Deletion of Leaf Deleting a node with no child Before deleting (3) After deleting (3) 15 Deletion Strategy: Delete the node
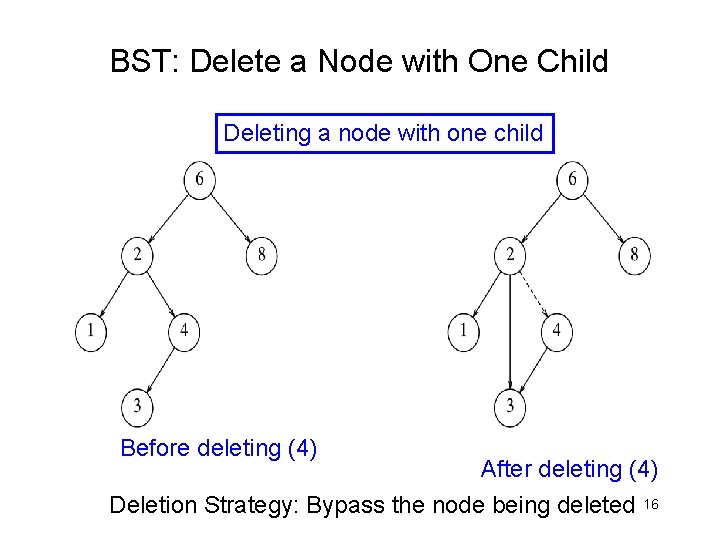
BST: Delete a Node with One Child Deleting a node with one child Before deleting (4) After deleting (4) Deletion Strategy: Bypass the node being deleted 16
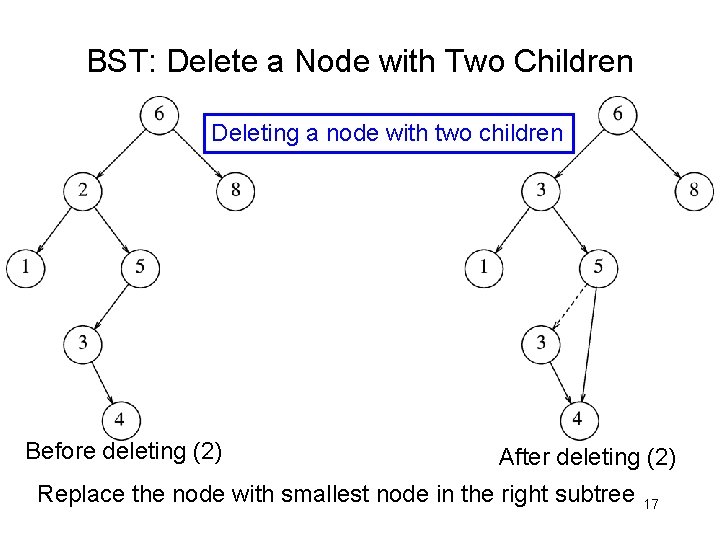
BST: Delete a Node with Two Children Deleting a node with two children Before deleting (2) After deleting (2) Replace the node with smallest node in the right subtree 17

BST: Deletion Code 18
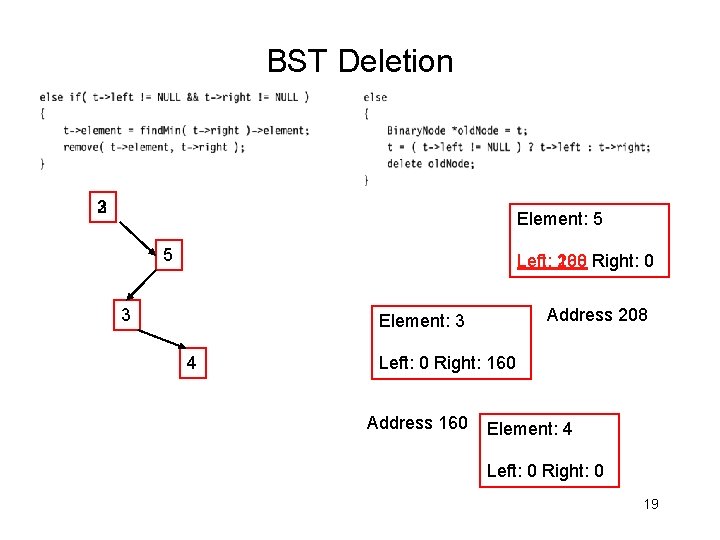
BST Deletion 2 3 Element: 5 5 Left: 160 208 Right: 0 3 Address 208 Element: 3 4 Left: 0 Right: 160 Address 160 Element: 4 Left: 0 Right: 0 19

BST: Lazy Deletion • Another deletion strategy – Don’t delete! – Just mark the node as deleted – Wastes space – But useful if deletions are rare or space is not a concern 20

BST: Insertion Bias • • Start with an empty tree Insert elements in sorted order What tree do you get? How do you fix it? 21

BST: Deletion Bias After large number of alternating insertions and deletions Why this bias? How do you fix it? 22

BST: Search using function objects 23
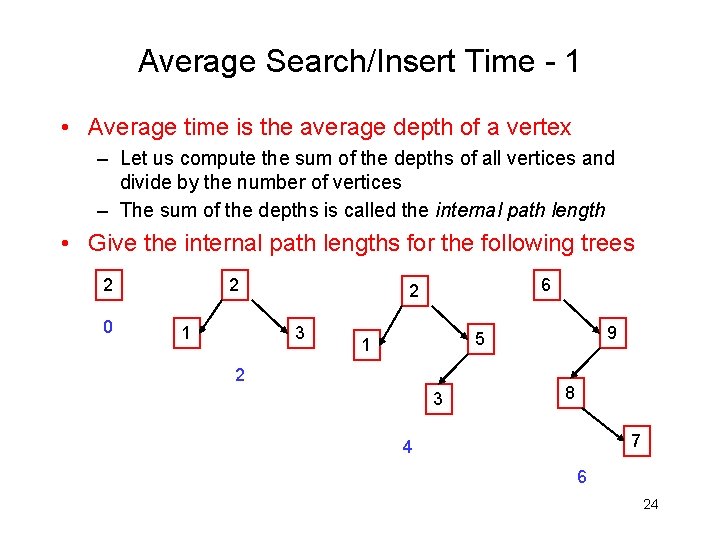
Average Search/Insert Time - 1 • Average time is the average depth of a vertex – Let us compute the sum of the depths of all vertices and divide by the number of vertices – The sum of the depths is called the internal path length • Give the internal path lengths for the following trees 2 0 2 1 6 2 3 9 5 1 2 3 8 7 4 6 24
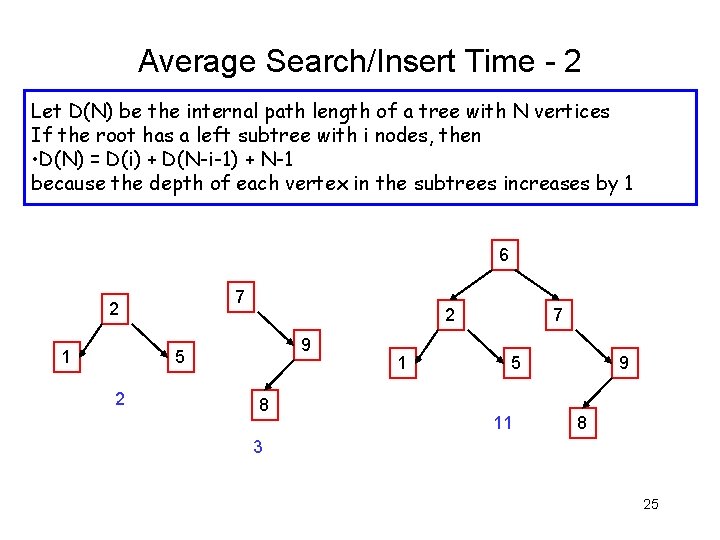
Average Search/Insert Time - 2 Let D(N) be the internal path length of a tree with N vertices If the root has a left subtree with i nodes, then • D(N) = D(i) + D(N-i-1) + N-1 because the depth of each vertex in the subtrees increases by 1 6 7 2 1 2 9 5 2 8 1 7 5 11 9 8 3 25
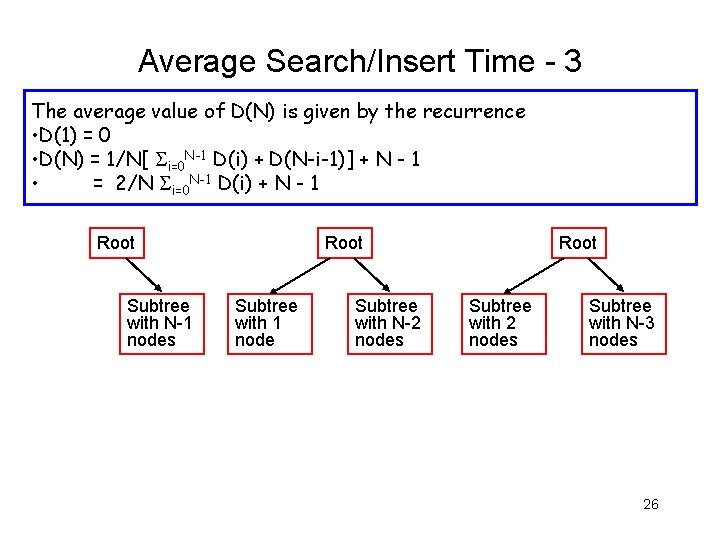
Average Search/Insert Time - 3 The average value of D(N) is given by the recurrence • D(1) = 0 • D(N) = 1/N[ i=0 N-1 D(i) + D(N-i-1)] + N - 1 • = 2/N i=0 N-1 D(i) + N - 1 Root Subtree with N-1 nodes Root Subtree with 1 node Subtree with N-2 nodes Root Subtree with 2 nodes Subtree with N-3 nodes 26

Average Search/Insert Time - 4 • D(N) = 2/N i=0 N-1 D(i) + N - 1 • N D(N) = 2 i=0 N-1 D(i) + N(N - 1) • (N-1)D(N-1) = 2 i=0 N-2 D(i) + (N-1)(N - 2) (2) - (1) gives • ND(N) - (N-1)D(N-1) = 2 D(N-1) + 2(N-1) • ND(N) = (N+1)D(N-1) + 2(N-1) • D(N)/(N+1) = D(N-1)/N + 2(N-1)/[N(N+1)] • < D(N-1)/N + 2/N (1) (2) • D(N)/(N+1) < D(N-1)/N + 2/N • D(N-1)/(N) < D(N-2)/(N-1) + 2/(N-1) • D(N-2)/(N-1) < D(N-3)/(N-2) + 2/(N-2) • . . . • D(2)/(3) < D(1)/2 + 2/2 27

Average Search/Insert Time - 5 • D(N)/(N+1) < D(N-1)/N + 2/N • D(N-1)/(N) < D(N-2)/(N-1) + 2/(N-1) • D(N-2)/(N-1) < D(N-3)/(N-2) + 2/(N-2) • . . . • D(2)/(3) < D(1)/2 + 2/2 • D(N)/(N+1) < D(N-1)/N + 2/N • < D(N-2)/(N-1) + 2/N • < D(N-3)/(N-2) + 2/(N-1) + 2/N • . . . • < D(1)/(2) + 2/2 +. . . + 2/(N-2) + 2/(N-1) + 2/N • = 2 i=2 N 1/i If we show that i=2 N 1/i is O(log N), then we can prove that average D(N) = O(N Log N) and so the average depth is O(log N) 28
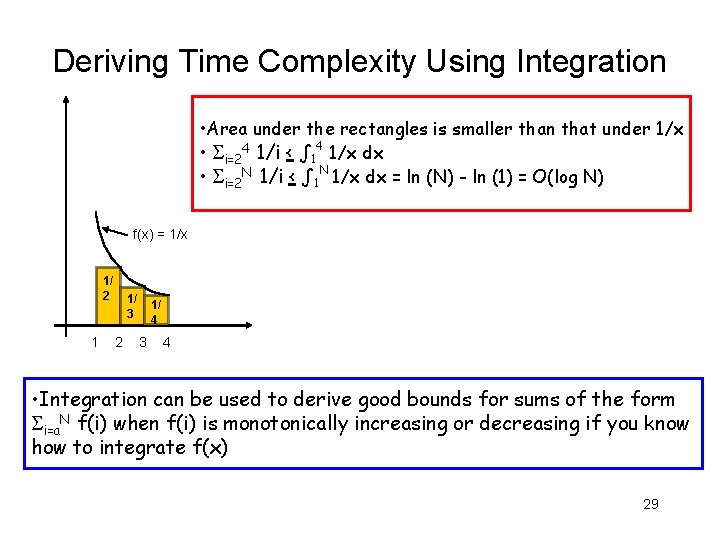
Deriving Time Complexity Using Integration • Area under the rectangles is smaller than that under 1/x • i=24 1/i < ∫ 14 1/x dx • i=2 N 1/i < ∫ 1 N 1/x dx = ln (N) - ln (1) = O(log N) f(x) = 1/x 1/ 2 1 1/ 3 2 1/ 4 3 4 • Integration can be used to derive good bounds for sums of the form i=a. N f(i) when f(i) is monotonically increasing or decreasing if you know how to integrate f(x) 29
- Slides: 29