TreeBased Methods Machine Learning BSMCGA 4439 Wenke Liu

Tree-Based Methods Machine Learning (BSMC-GA 4439) Wenke Liu 10 -22 -2019

Outline �Basic tree models � Classification and Regression Tree (CART) �Bagging trees � Random forest �Boosting trees � Ada. Boost � Gradient boosting

Tree-based methods � Partition the feature space (X) into rectangles and fit a simple model to each region. � Recursive binary splits represented by trees.

Basic Trees �Grow � Recursive binary split to achieve outcome homogeneity within nodes (leaves) � Find the best splitting variable and split point at each step �Stop � Stop splitting when minimal node size or maximal depth is reached �Prune � Cut back the tree to prevent over fitting

Tree-based methods � Tree methods can be used to predict both categorical and continuous responses. � In regression tree models, the response (Y) is continuous. � In classification tree models, the response (Y) is categorical (usually binary). � The features (X) can be either categorical or continuous in both cases. � Different splitting and pruning criteria for regression and classification trees.

Basic regression tree �

Cost complexity pruning �

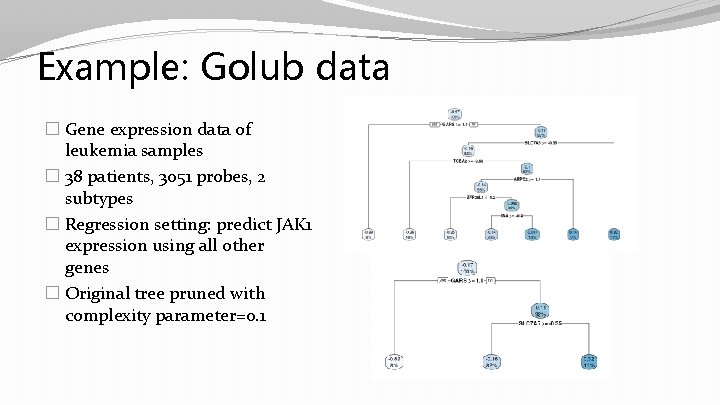
Example: Golub data � Gene expression data of leukemia samples � 38 patients, 3051 probes, 2 subtypes � Regression setting: predict JAK 1 expression using all other genes � Original tree pruned with complexity parameter=0. 1

Summary of regression tree algorithm ITSL p 309

Classification tree � The major difference between regression tree and classification tree is the cost function to minimize at each split: � Prediction with majority vote. � All the cost functions above are generalizable to k-class outcomes. � Usually, classification trees are built with Gini index or deviance, but pruned with misclassification error.

Handling missing data � Tree-based models can easily handle predictor missing values. � A ‘missing’ level can be constructed for categorical variables. � Surrogate split � Only consider non-missing observations when selecting split predictor and split value. � Construct a rank list of other predictors that produce similar splits. � If the split predictor is missing in a future observation, use the surrogate predictors in order.

Feature importance �

Summary of decision tree model � Advantage � Interpretability � Can model nonlinear functions � Disadvantage � Relatively high prediction error, especially in regression setting (because each partition is modeled as constants) � Tends to overfit training data and produce unstable models

Ensemble methods � Disadvantages of single trees can be (at least partially) remedied by making ensembles that combine multiple models. � Bagging trees: reduce variance, improve stability. � Boosting trees: reduce bias, improve prediction accuracy and flexibility.

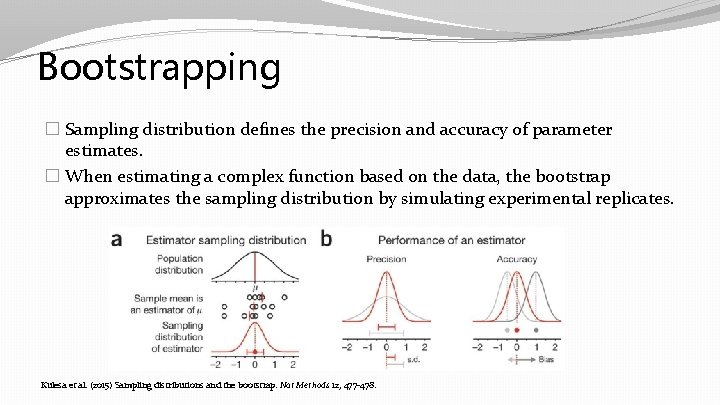
Bootstrapping � Sampling distribution defines the precision and accuracy of parameter estimates. � When estimating a complex function based on the data, the bootstrap approximates the sampling distribution by simulating experimental replicates. Kulesa et al. (2015) Sampling distributions and the bootstrap. Nat Methods 12, 477 -478.

Bootstrap aggregation (Bagging) �

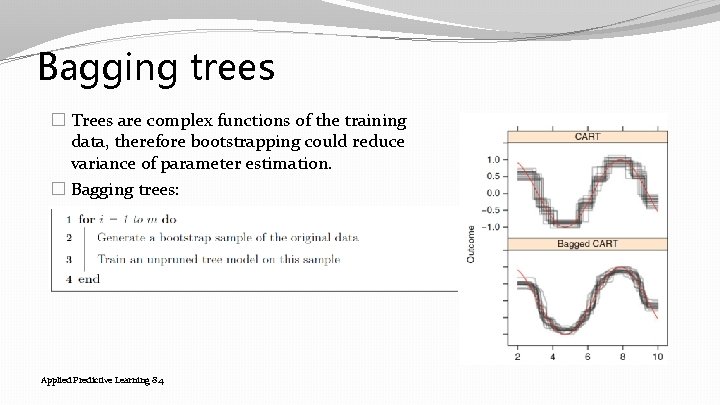
Bagging trees � Trees are complex functions of the training data, therefore bootstrapping could reduce variance of parameter estimation. � Bagging trees: Applied Predictive Learning 8. 4

Random forest � Random forest is a further extension to bagging trees. � The power of bagging is limited by correlations among individual bagged models. � Random forest de-correlate trees in the ensemble. � Very little hyper-parameter tuning is required.

Random forest �

Out of bag (OOB) samples � For each observation, a subset of the RF ensemble is built with bootstrap samples in which it did not appear. This observation is an out of bag sample for the subset of trees. � OOB samples can be used to: � Evaluate prediction error (OOB error) � Estimate variable importance (permute OOB values of predictors and record change of model accuracy) � Similarity with cross-validation. OOB error is a good estimate for ‘real’ test error

Boosting � Combine weak learners to form a powerful model (additive modeling). � Different from bagging, trees in the boosting ensemble are not independent, but grown sequentially. � Boosting improves the prediction error by making the model smoother.

Ada. Boost � Boosting tree for binary classification. � Give more weights to misclassified samples.

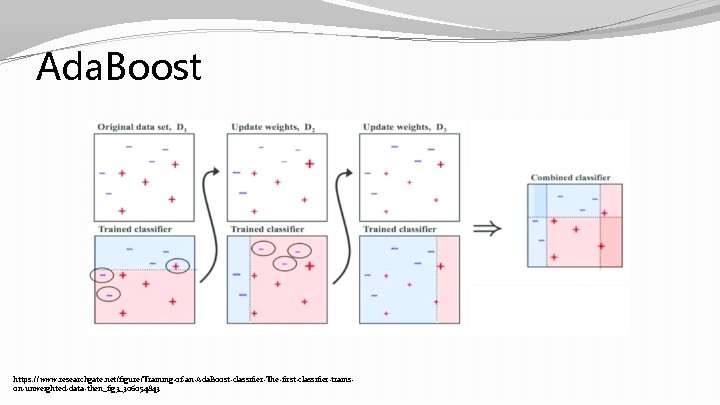
Ada. Boost https: //www. researchgate. net/figure/Training-of-an-Ada. Boost-classifier-The-first-classifier-trainson-unweighted-data-then_fig 3_306054843

Boosting as additive modeling �

Boosting as additive modeling �

Gradient Boosting Tree � Use gradient descent to reduce loss in each iteration. � Generalizable to all differentiable loss functions. � Hyper-parameters: � Number of iterations M � Number of terminal nodes J

Gradient Boosting Tree �

Summary � Tree-based methods are popular ‘off-the-shelf’ models. � Suitable for nonlinear and high-dimensional data. � Successful models such as random forest and xgboost trade interpretability for predictive power.