Tree Traversal Section 9 3 Longin Jan Latecki



![inorder (t) if t != NIL: { inorder (left[t]); write (label[t]); inorder (right[t]); } inorder (t) if t != NIL: { inorder (left[t]); write (label[t]); inorder (right[t]); }](https://slidetodoc.com/presentation_image_h/ef41a5dbdf79c48cb563fc2d3246eda5/image-16.jpg)


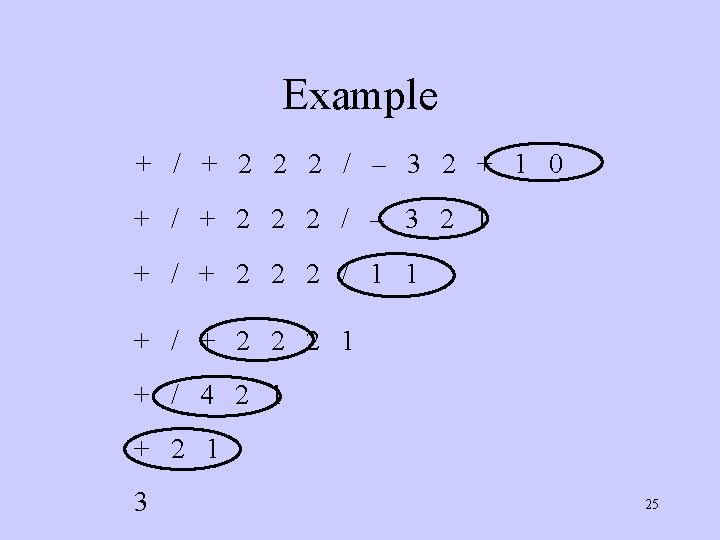


- Slides: 28

Tree Traversal Section 9. 3 Longin Jan Latecki Temple University Based on slides by Paul Tymann, Andrew Watkins, and J. van Helden 1

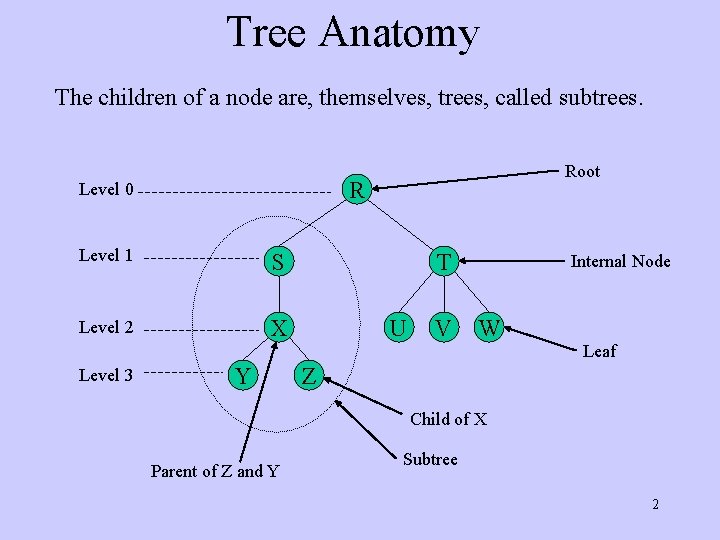
Tree Anatomy The children of a node are, themselves, trees, called subtrees. R Level 0 Level 1 S Level 2 X Level 3 Root Y T U V Internal Node W Leaf Z Child of X Parent of Z and Y Subtree 2

Tree Traversals • One of the most common operations performed on trees, are a tree traversals • A traversal starts at the root of the tree and visits every node in the tree exactly once – visit means to process the data in the node • Traversals are either depth-first or breadthfirst 3

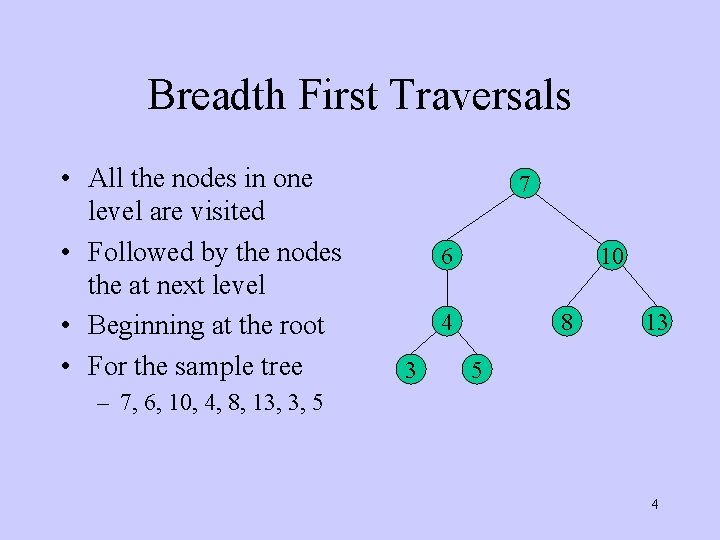
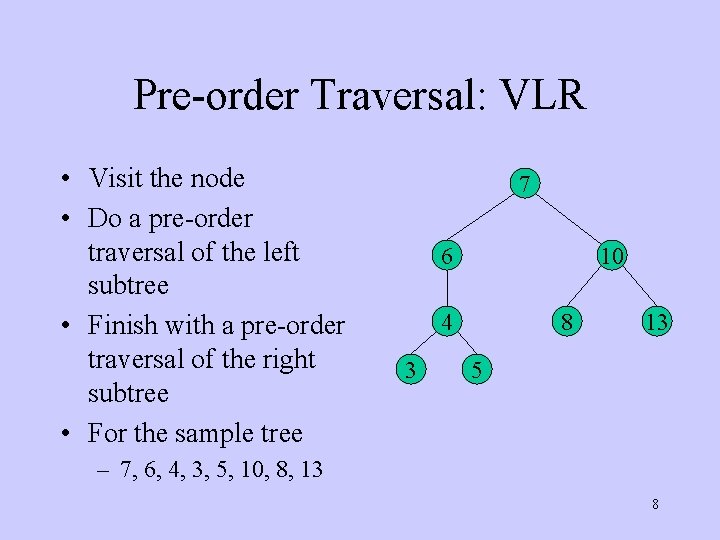
Breadth First Traversals • All the nodes in one level are visited • Followed by the nodes the at next level • Beginning at the root • For the sample tree 7 6 10 4 3 8 13 5 – 7, 6, 10, 4, 8, 13, 3, 5 4

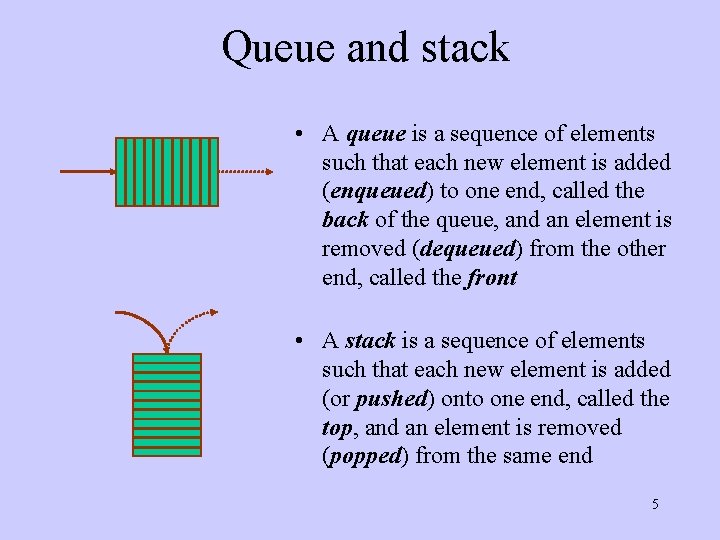
Queue and stack • A queue is a sequence of elements such that each new element is added (enqueued) to one end, called the back of the queue, and an element is removed (dequeued) from the other end, called the front • A stack is a sequence of elements such that each new element is added (or pushed) onto one end, called the top, and an element is removed (popped) from the same end 5

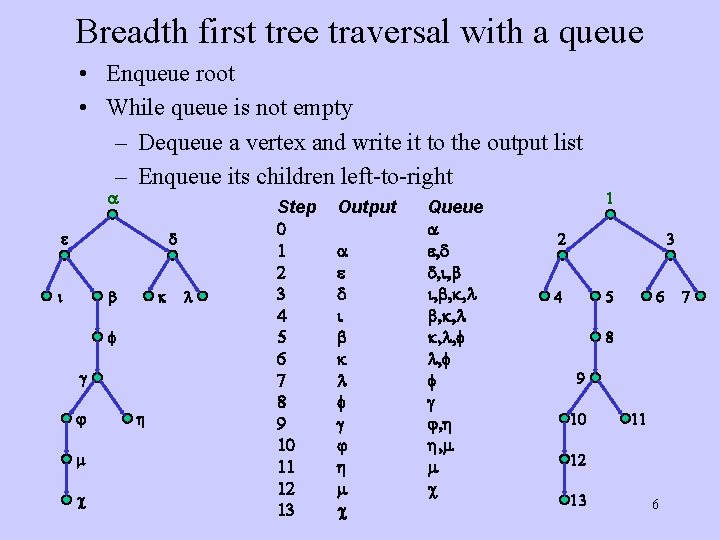
Breadth first tree traversal with a queue • Enqueue root • While queue is not empty – Dequeue a vertex and write it to the output list – Enqueue its children left-to-right a e d i b k f g j m c h l Step 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Output a e d i b k l f g j h m c Queue a e, d d, i, b, k, l, f l, f f g j, h h, m m c 1 2 3 4 5 6 8 9 10 11 12 13 6 7

Depth-First Traversals • There are 8 different depth-first traversals – VLR (pre-order traversal) – VRL – LVR (in-order traversal) – RVL – RLV – LRV (post-order traversal) 7

Pre-order Traversal: VLR • Visit the node • Do a pre-order traversal of the left subtree • Finish with a pre-order traversal of the right subtree • For the sample tree 7 6 10 4 3 8 13 5 – 7, 6, 4, 3, 5, 10, 8, 13 8

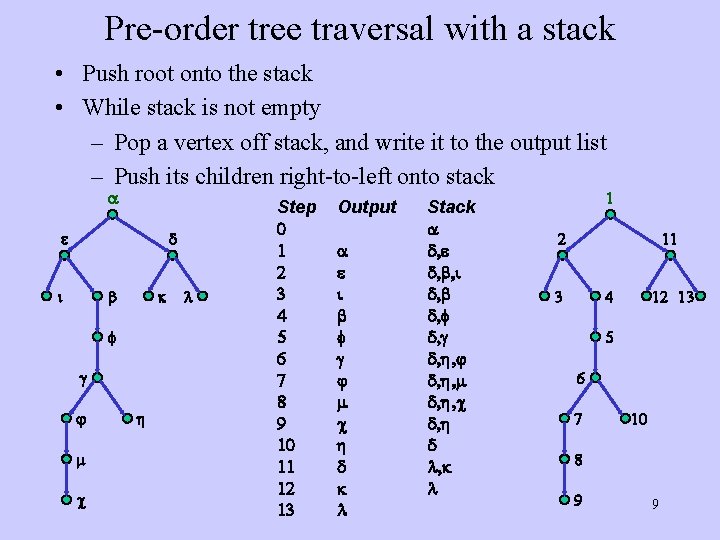
Pre-order tree traversal with a stack • Push root onto the stack • While stack is not empty – Pop a vertex off stack, and write it to the output list – Push its children right-to-left onto stack a e d i b k f g j m c h l Step 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Output a e i b f g j m c h d k l Stack a d, e d, b, i d, b d, f d, g d, h, j d, h, m d, h, c d, h d l, k l 1 2 11 3 4 12 13 5 6 7 10 8 9 9

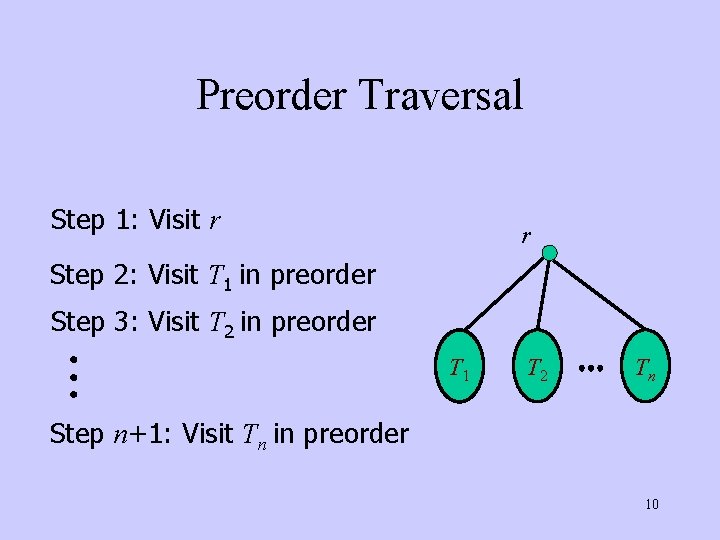
Preorder Traversal Step 1: Visit r r Step 2: Visit T 1 in preorder Step 3: Visit T 2 in preorder T 1 T 2 Tn Step n+1: Visit Tn in preorder 10

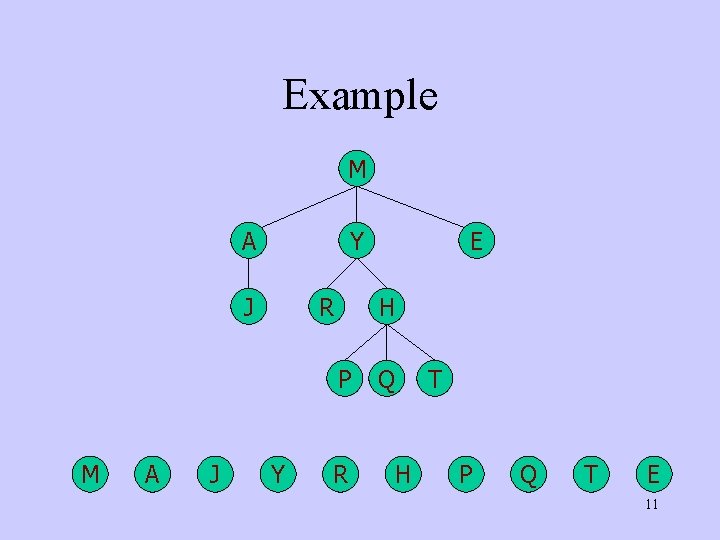
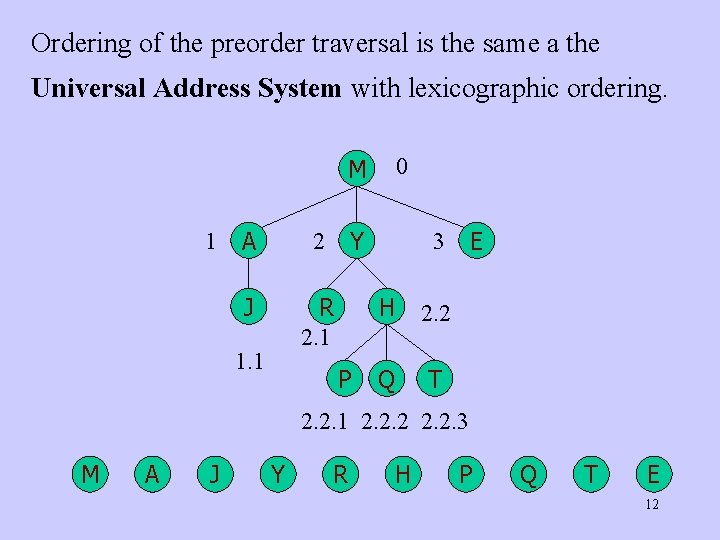
Example M A Y J R H P M A J Y E R Q H T P Q T E 11

Ordering of the preorder traversal is the same a the Universal Address System with lexicographic ordering. 0 M 1 A 2 J R 2. 1 1. 1 Y P E 3 H 2. 2 Q T 2. 2. 1 2. 2. 2. 3 M A J Y R H P Q T E 12

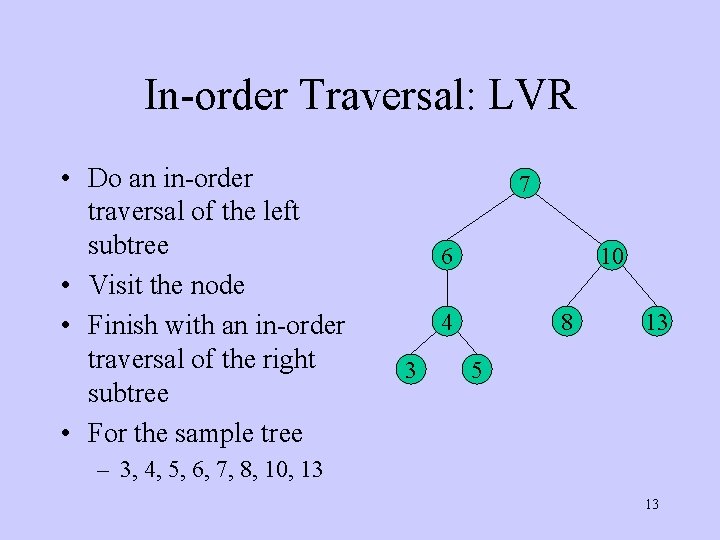
In-order Traversal: LVR • Do an in-order traversal of the left subtree • Visit the node • Finish with an in-order traversal of the right subtree • For the sample tree 7 6 10 4 3 8 13 5 – 3, 4, 5, 6, 7, 8, 10, 13 13

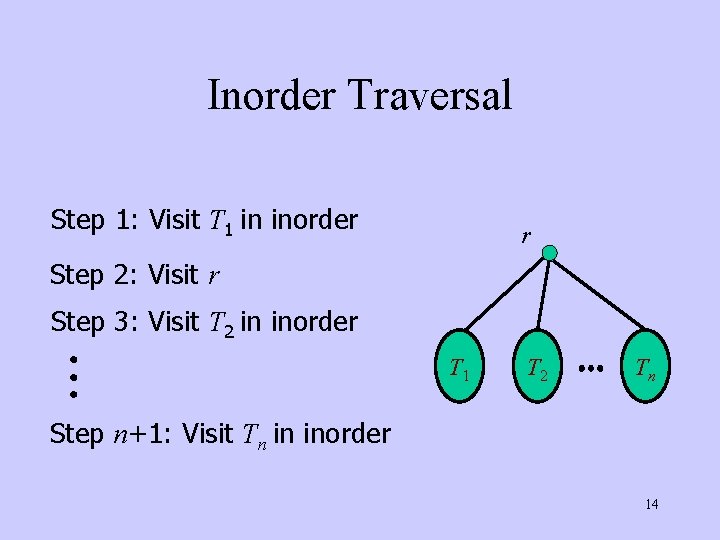
Inorder Traversal Step 1: Visit T 1 in inorder r Step 2: Visit r Step 3: Visit T 2 in inorder T 1 T 2 Tn Step n+1: Visit Tn in inorder 14

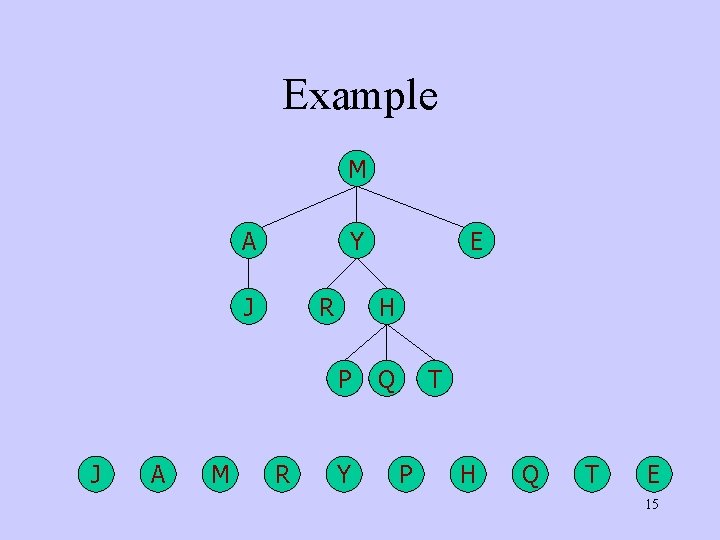
Example M A Y J R H P J A M R E Y Q T P H Q T E 15
![inorder t if t NIL inorder leftt write labelt inorder rightt inorder (t) if t != NIL: { inorder (left[t]); write (label[t]); inorder (right[t]); }](https://slidetodoc.com/presentation_image_h/ef41a5dbdf79c48cb563fc2d3246eda5/image-16.jpg)
inorder (t) if t != NIL: { inorder (left[t]); write (label[t]); inorder (right[t]); } Inorder Traversal on a binary search tree. 16

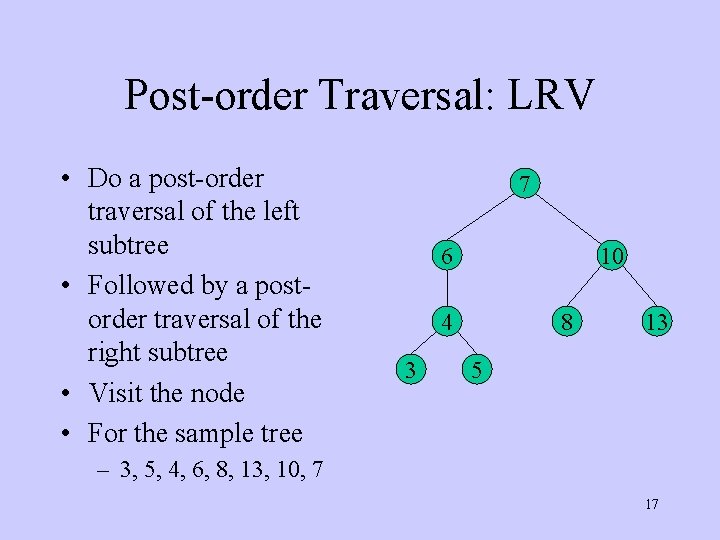
Post-order Traversal: LRV • Do a post-order traversal of the left subtree • Followed by a postorder traversal of the right subtree • Visit the node • For the sample tree 7 6 10 4 3 8 13 5 – 3, 5, 4, 6, 8, 13, 10, 7 17

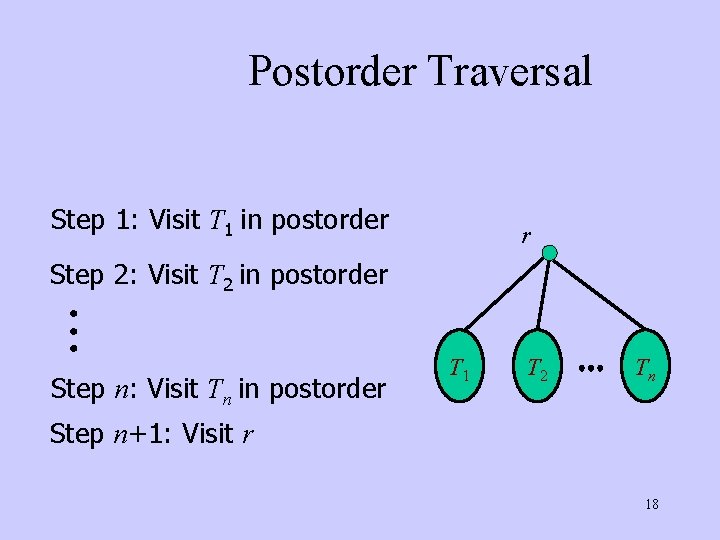
Postorder Traversal Step 1: Visit T 1 in postorder r Step 2: Visit T 2 in postorder Step n: Visit Tn in postorder T 1 T 2 Tn Step n+1: Visit r 18

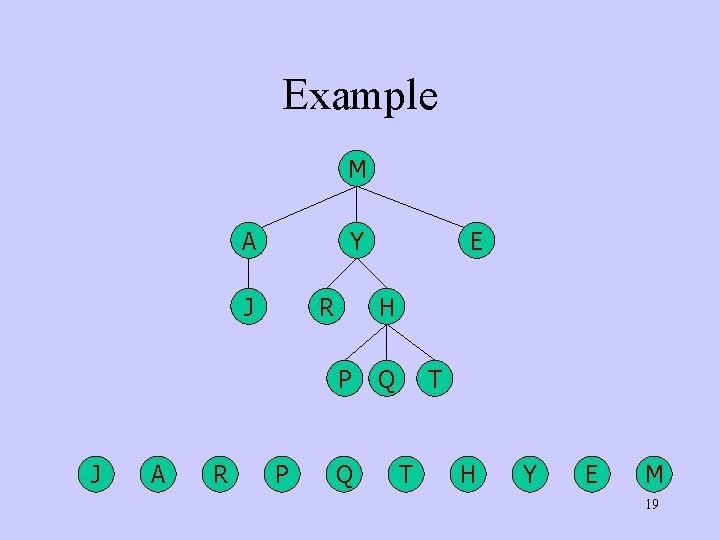
Example M A Y J R H P J A R P E Q Q T T H Y E M 19

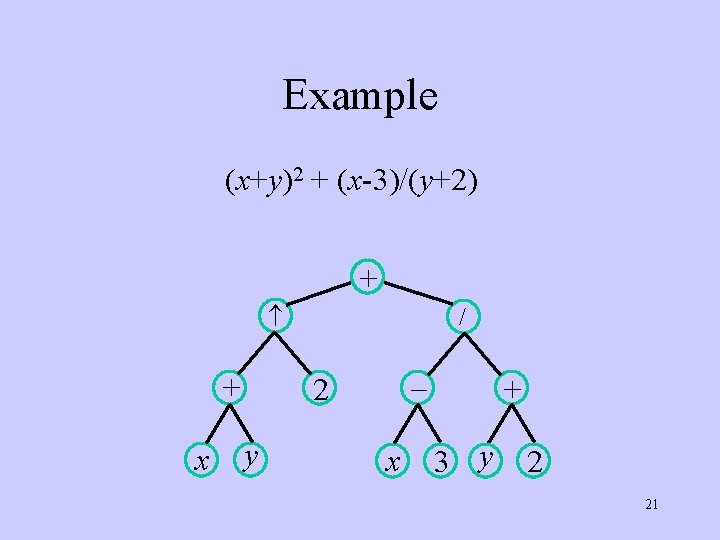
Representing Arithmetic Expressions • Complicated arithmetic expressions can be represented by an ordered rooted tree – Internal vertices represent operators – Leaves represent operands • Build the tree bottom-up – Construct smaller subtrees – Incorporate the smaller subtrees as part of larger subtrees 20

Example (x+y)2 + (x-3)/(y+2) + + x / – 2 y x + 3 y 2 21

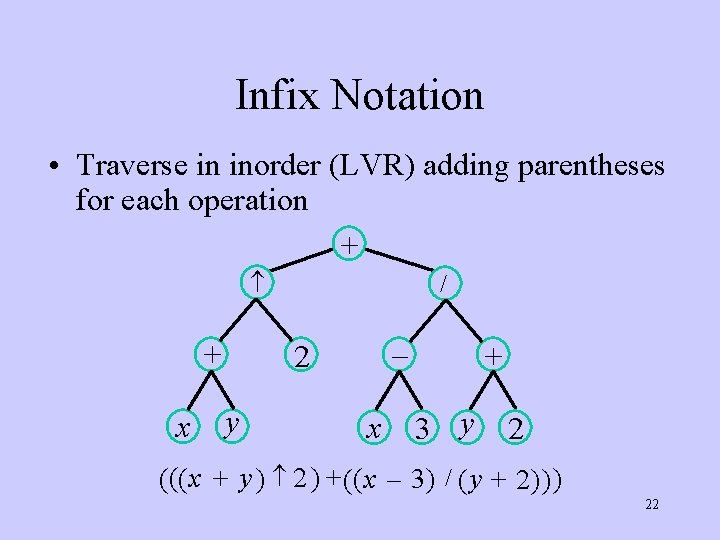
Infix Notation • Traverse in inorder (LVR) adding parentheses for each operation + + x / – 2 y x + 3 y 2 ( (( x + y ) 2 ) +( ( x – 3 ) / ( y + 2 ) ) ) 22

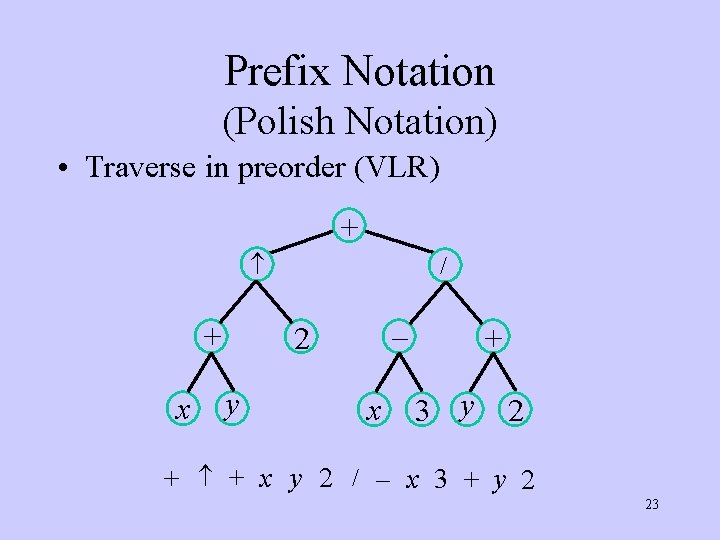
Prefix Notation (Polish Notation) • Traverse in preorder (VLR) + + x / – 2 y x + 3 y 2 + + x y 2 / – x 3 + y 2 23

Evaluating Prefix Notation • In an prefix expression, a binary operator precedes its two operands • The expression is evaluated right-left • Look for the first operator from the right • Evaluate the operator with the two operands immediately to its right 24
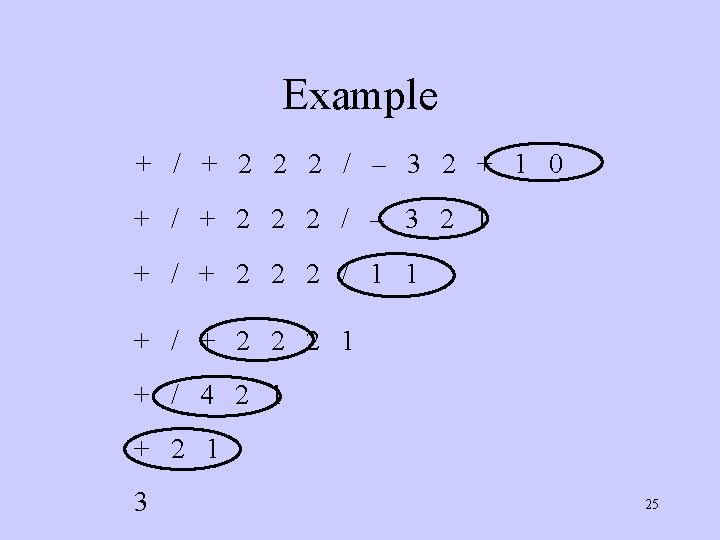
Example + / + 2 2 2 / – 3 2 + 1 0 + / + 2 2 2 / – 3 2 1 + / + 2 2 2 / 1 1 + / + 2 2 2 1 + / 4 2 1 + 2 1 3 25

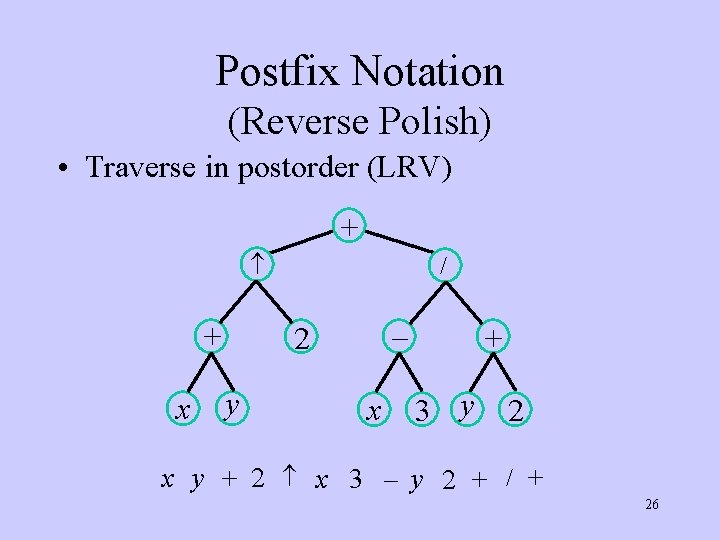
Postfix Notation (Reverse Polish) • Traverse in postorder (LRV) + + x / – 2 y x + 3 y 2 x y + 2 x 3 – y 2 + / + 26

Evaluating Postfix Notation • In an postfix expression, a binary operator follows its two operands • The expression is evaluated left-right • Look for the first operator from the left • Evaluate the operator with the two operands immediately to its left 27

Example 2 2 + 2 / 3 2 – 1 0 + / + 4 2 / 3 2 – 1 0 + / + 2 1 1 / + 2 1 + 3 28