Tree Searching Strategies 1 n n The procedure

Tree Searching Strategies 1

n n The procedure of solving many problems may be represented by trees. Therefore the solving of these problems becomes a tree searching problem. 2

Satisfiability problem Tree Representation of Eight Assignments. If there are n variables x 1, x 2, …, xn, then there are 2 n possible assignments. 3

Satisfiability problem n An instance: -x 1……. . ……(1) x 1…………. . (2) x 2 v x 5…. …. (3) x 3……. (4) -x 2……. (5) n A Partial Tree to Determine the Satisfiability Problem. We may not need to examine all possible assignments. 4

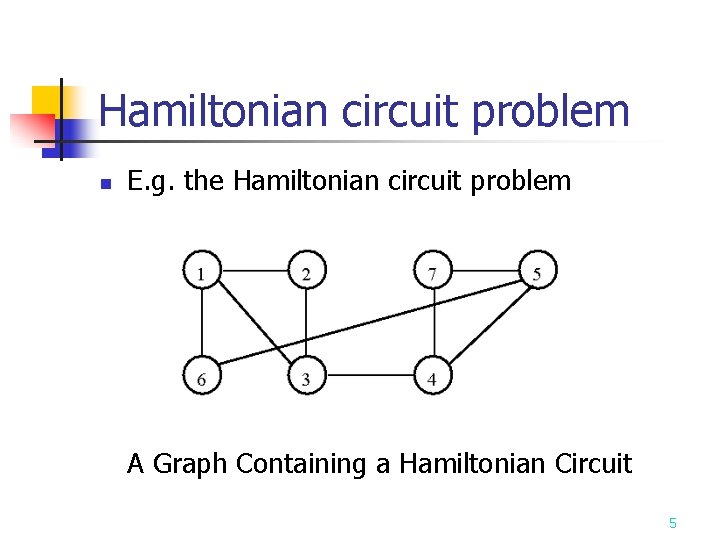
Hamiltonian circuit problem n E. g. the Hamiltonian circuit problem A Graph Containing a Hamiltonian Circuit 5

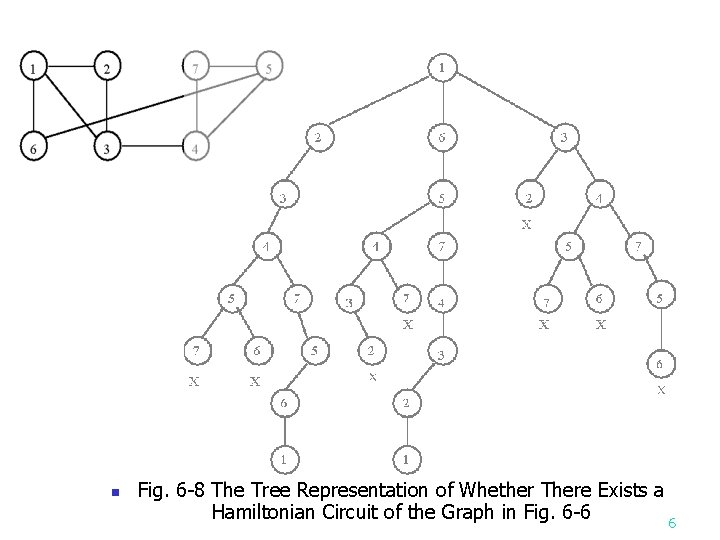
n Fig. 6 -8 The Tree Representation of Whether There Exists a Hamiltonian Circuit of the Graph in Fig. 6 -6 6

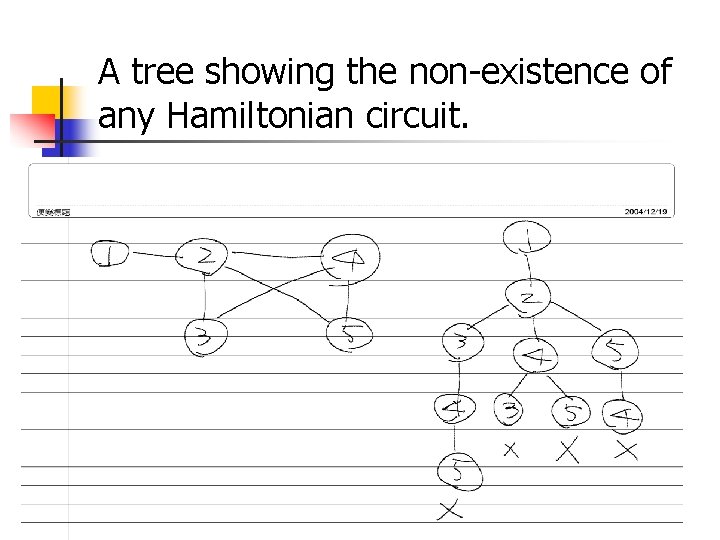
A tree showing the non-existence of any Hamiltonian circuit. 7

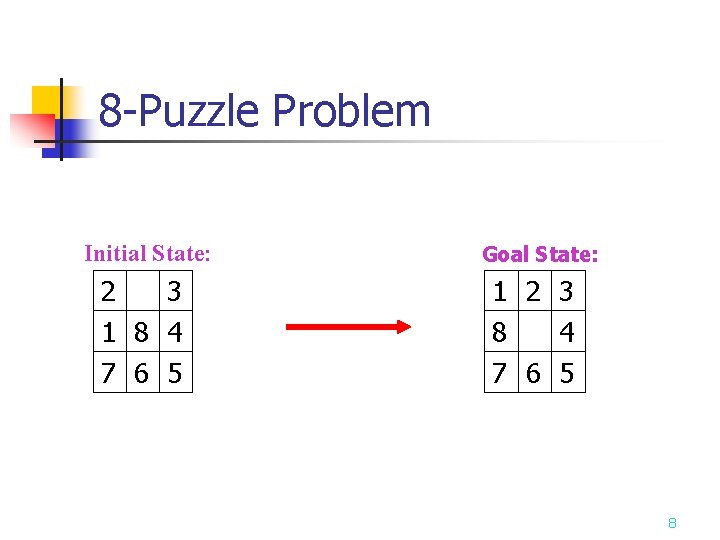
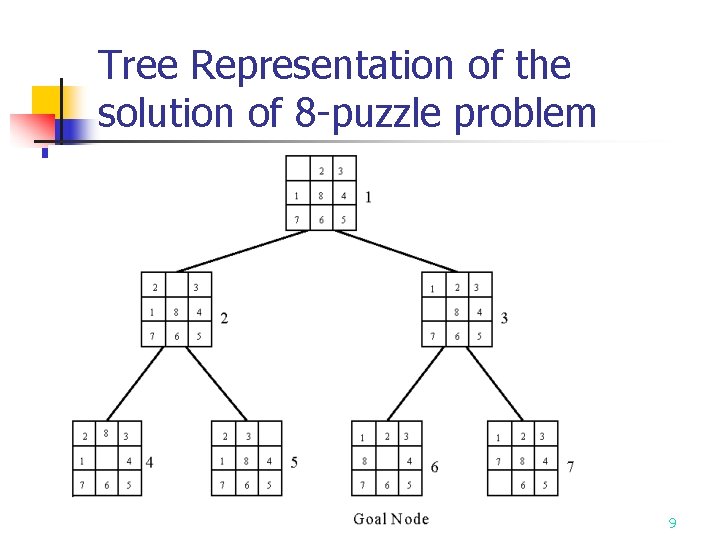
8 -Puzzle Problem Initial State: 2 3 1 8 4 7 6 5 Goal State: 1 2 3 8 4 7 6 5 8

Tree Representation of the solution of 8 -puzzle problem 9

How to expand the tree ? n n Breadth-First Search Depth-First Search Hill Climbing Best-First Search 10

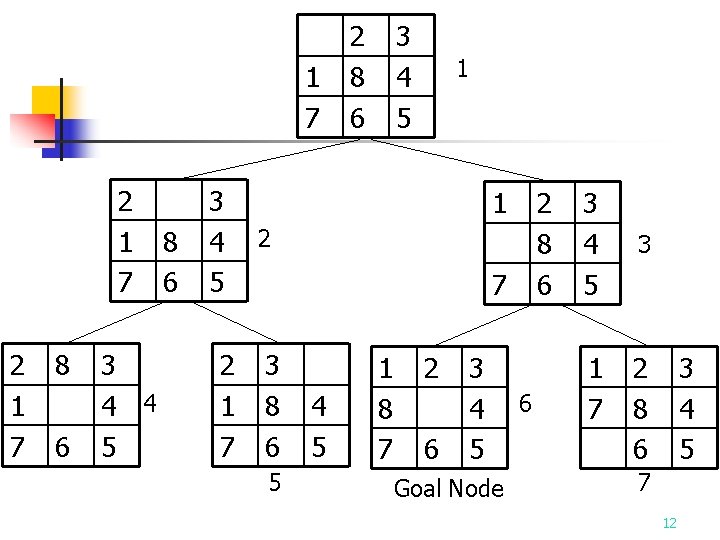
Breadth-First Search Scheme n n Step 1: Step 1 Form a one-element queue consisting of the root node. Step 2: Step 2 Test to see if the first element in the queue is a goal node. If it is, stop. Otherwise, go to step 3. Step 3: Step 3 Remove the first element from the queue. Add the first element’s descendants, if any, to the end of the queue. Step 4: Step 4 If the queue is empty, then signal failure. Otherwise, go to Step 2. 11

1 7 2 1 7 8 6 3 4 5 8 6 4 3 4 5 2 1 7 2 8 6 3 4 5 1 1 2 8 6 2 7 3 8 6 5 4 5 1 8 7 2 6 3 4 5 Goal Node 6 3 4 5 1 7 3 2 8 6 3 4 5 7 12

Depth-First Search Scheme n n Step 1: Step 1 Form a one-element stack consisting of the root node. Step 2: Step 2 Test to see if the top element in the queue is a goal node. If it is, stop. Otherwise, go to step 3. Step 3: Step 3 Remove the top element from the stack. Add the first element’s descendants, if any, to the top of the stack. Step 4: Step 4 If the stack is empty, then signal failure. Otherwise, go to Step 2. 13

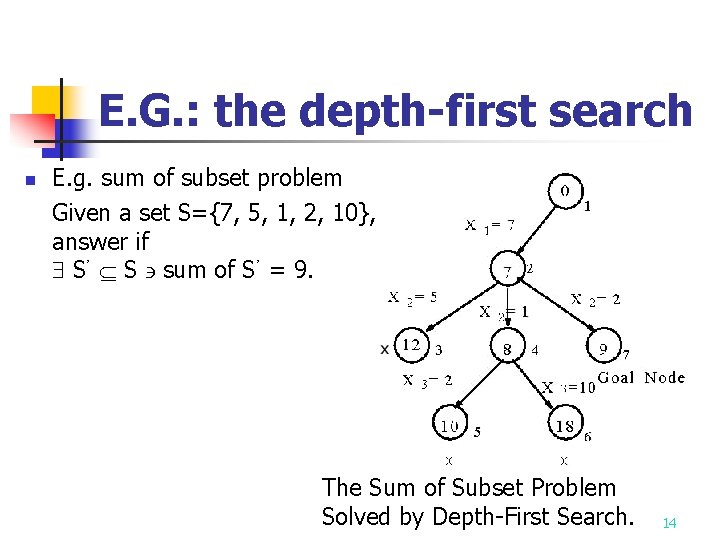
E. G. : the depth-first search n E. g. sum of subset problem Given a set S={7, 5, 1, 2, 10}, answer if S’ S sum of S’ = 9. The Sum of Subset Problem Solved by Depth-First Search. 14

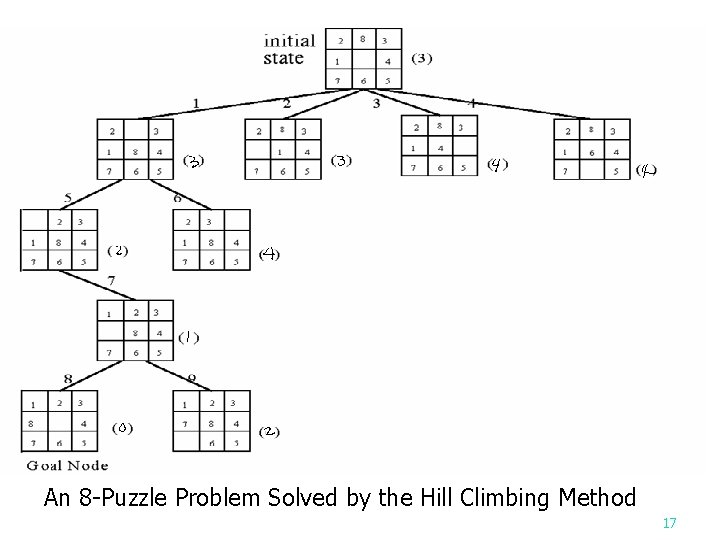
Hill climbing n A variant of depth-first search The method selects the locally optimal node to expand. n E. g. for the 8 -puzzle problem, evaluation function f(n) = w(n), where w(n) is the number of misplaced tiles in node n. 15

Hill Climbing Search Scheme n n Step 1: Step 1 Form a one-element stack consisting of the root node. Step 2: Step 2 Test to see if the top element in the queue is a goal node. If it is, stop. Otherwise, go to step 3. Step 3: Step 3 Remove the top element from the stack. Add the first element’s descendants, if any, to the top of the stack according to order computed by the evaluation function. Step 4: Step 4 If the stack is empty, then signal failure. Otherwise, go to Step 2. 16

An 8 -Puzzle Problem Solved by the Hill Climbing Method 17

Best-first search strategy n n n Combing depth-first search and breadth-first search Selecting the node with the best estimated cost among all nodes. This method has a global view. 18

Best-First Search Scheme n n Step 1: Consturct a heap by using the Step 1 evaluation function. First, form a 1 -element heap consisting of the root node. Step 2: Test to see if the root element in the Step 2 heap is a goal node. If it is, stop; otherwise, go to Step 3: Remove the root element from the Step 3 heap and expand the element. Add the descendants of the element into the heap. Step 4: If Step 4 the heap is empty, then signal failure. Otherwise, go to Step 2. 19

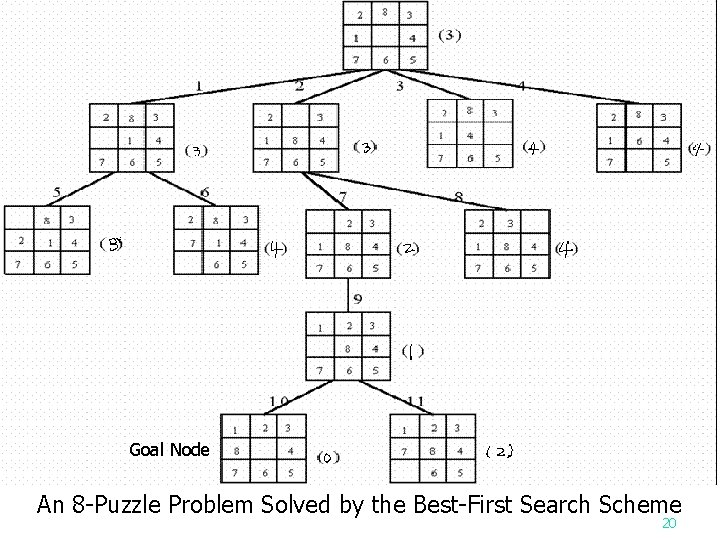
Goal Node An 8 -Puzzle Problem Solved by the Best-First Search Scheme 20

Q&A 21