Tree Recursion Traditional Approach Tree Recursion Consider the

Tree Recursion Traditional Approach

Tree Recursion • Consider the Fibonacci Number Sequence: Time: 0 1 2 3 4 5 6 7 8 0, 1, 1, 2, 3, 5, 8, 13, 21, . . . / 0 fib(n) = | 1 fib(n - 1) + fib(n - 2) when n = 0 when n = 1 otherwise

Tree Recursion • (cont. ) As code this is: int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(4) fib(3) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(4) fib(3) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

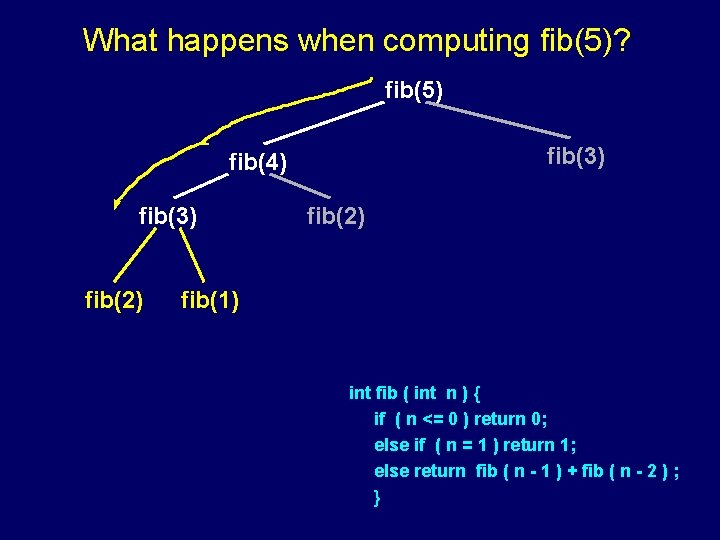
What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

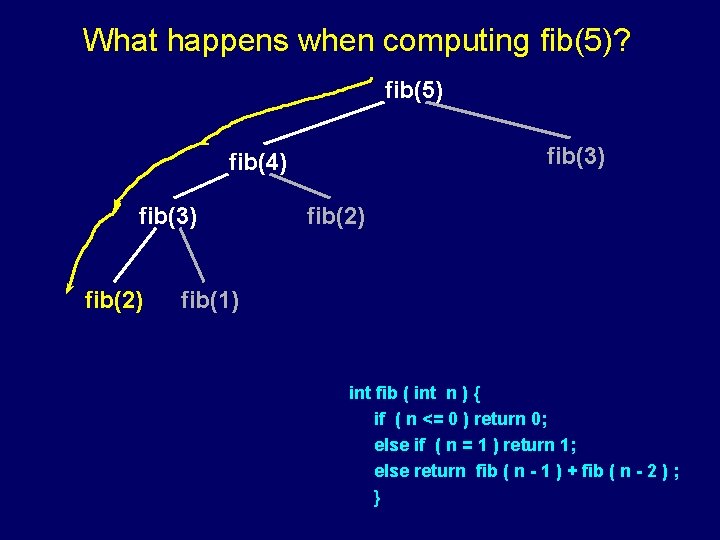
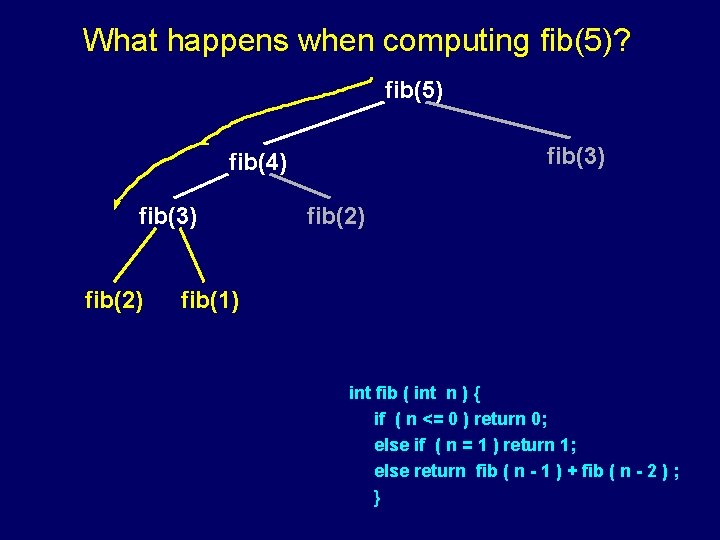
What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) fib(1) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) fib(1) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

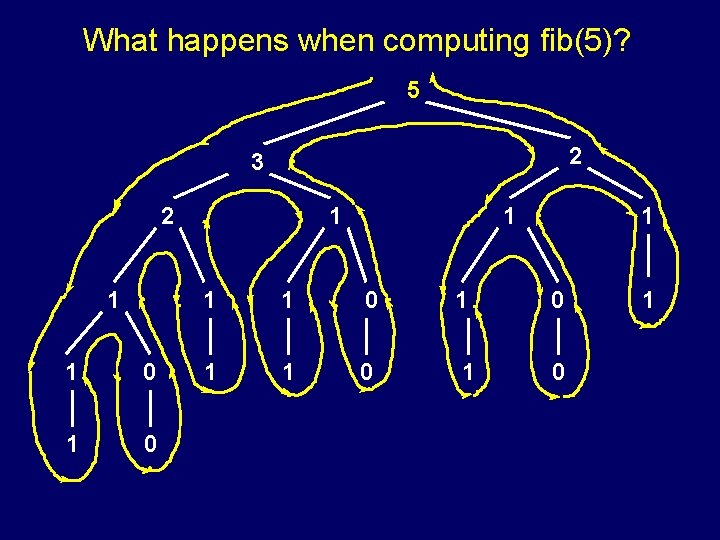
What happens when computing fib(5)? 5 2 3 2 1 1 0 1 0 1

What is the Problem? • I am explaining everything! • Why not make this more interesting by using MS Agents • • Agents are helpers like the paper clip in Word But they are much more: • They talk to you • And can, in some cases, understand voice commands

Tree Recursion MS Agent Approach

Tree Recursion • Consider the Fibonacci Number Sequence: Time: 0 1 2 3 4 5 6 7 8 0, 1, 1, 2, 3, 5, 8, 13, 21, . . . u This sequence is defined by the rule: / 0 when n = 0 fib(n) = | 1 when n = 1 fib(n - 1) + fib(n - 2) otherwise

Tree Recursion • (cont. ) As code this is: int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(4) fib(3) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(4) fib(3) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

What happens when computing fib(5)? fib(5) fib(3) fib(4) fib(3) fib(2) fib(1) int fib ( int n ) { if ( n <= 0 ) return 0; else if ( n = 1 ) return 1; else return fib ( n - 1 ) + fib ( n - 2 ) ; }

MASH: Microsoft Agent Scripting Helper MASH is an editor that allows you to construct the scripts that you can then embed in other applications MASH

Where to Learn More • MS Agent Page: http: //msdn. microsoft. com/workshop/imedia/agent/default. asp • Sunfires MS Agent Page: http: //www. angelfire. com/il 2/sunfire/index. html • Uniquities MS Agent Planet: http: //www. uniquities. co. uk/whatsnew. htm • Presentation Narrator: http: //msdn. microsoft. com/workshop/imedia/agent/sampleoffice. asp • Microsoft Agent Scripting Helper: http: //www. bellcraft. com/mash/