Tree diagrams MATHSWATCH CLIP 151 175 204 GRADE

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 L. O. To be able to § Complete a tree diagram to show probabilities Key Words probability, and, or, at least, total, independent, replacement, non-replacement

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 https: //www. youtube. com/watch? v=k. NOr. DWm 15 b. Y

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 WITH REPLACEMENT

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Tree diagrams § Help you to solve probability problems where one thing is happening after another (after another…) § For example Ø picking two or more items out from a selection Ø playing two or more different games Ø considering whether something will happen on two or more different days, etc. § You can use fractions or decimals to show the probabilities in a tree diagram § We are going to look at INDEPENDENT events first

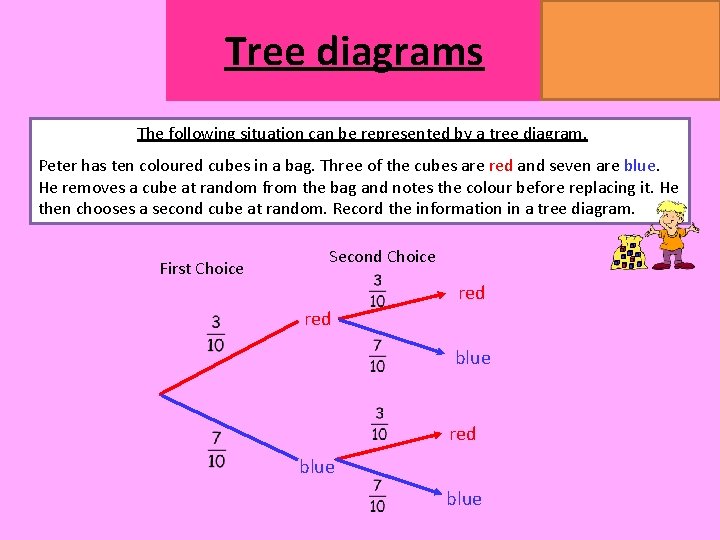
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 The following situation can be represented by a tree diagram. Peter has ten coloured cubes in a bag. Three of the cubes are red and seven are blue. He removes a cube at random from the bag and notes the colour before replacing it. He then chooses a second cube at random. Record the information in a tree diagram. First Choice Second Choice red blue

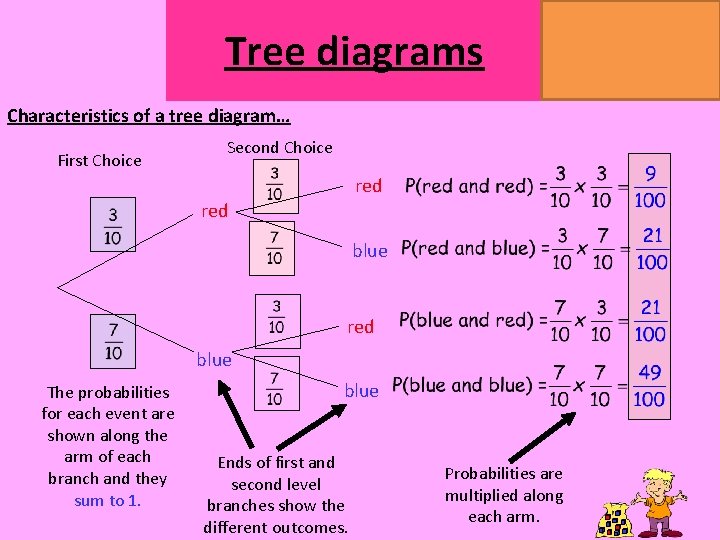
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Characteristics of a tree diagram… First Choice Second Choice red blue The probabilities for each event are shown along the arm of each branch and they sum to 1. blue Ends of first and second level branches show the different outcomes. Probabilities are multiplied along each arm.

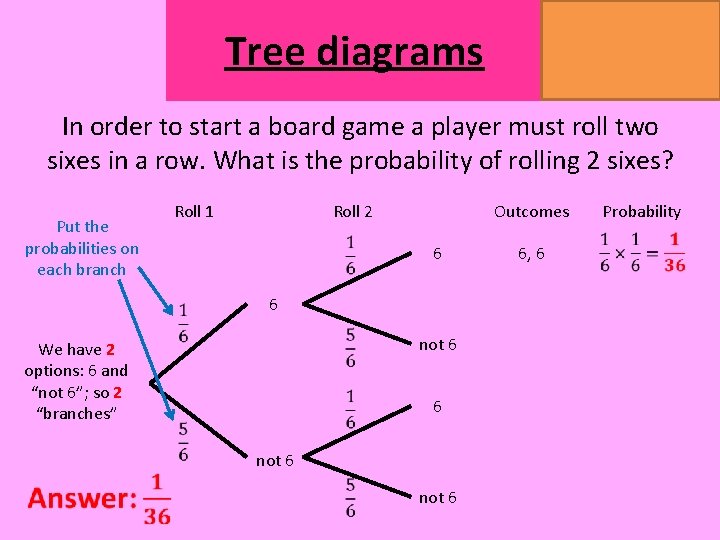
MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Tree diagrams In order to start a board game a player must roll two sixes in a row. What is the probability of rolling 2 sixes? Put the probabilities on each branch Roll 2 Roll 1 Outcomes 6 6 not 6 We have 2 options: 6 and “not 6”; so 2 “branches” 6 not 6 6, 6 Probability

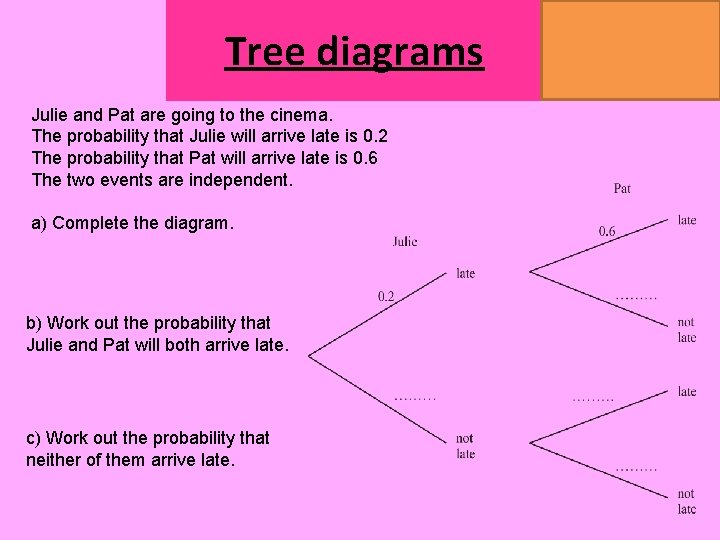
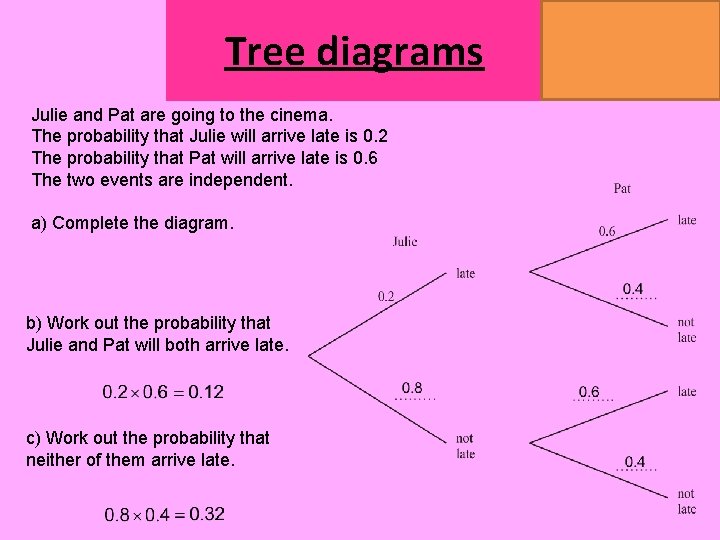
Tree diagrams Julie and Pat are going to the cinema. The probability that Julie will arrive late is 0. 2 The probability that Pat will arrive late is 0. 6 The two events are independent. a) Complete the diagram. b) Work out the probability that Julie and Pat will both arrive late. c) Work out the probability that neither of them arrive late. MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7

Tree diagrams Julie and Pat are going to the cinema. The probability that Julie will arrive late is 0. 2 The probability that Pat will arrive late is 0. 6 The two events are independent. a) Complete the diagram. b) Work out the probability that Julie and Pat will both arrive late. c) Work out the probability that neither of them arrive late. MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7

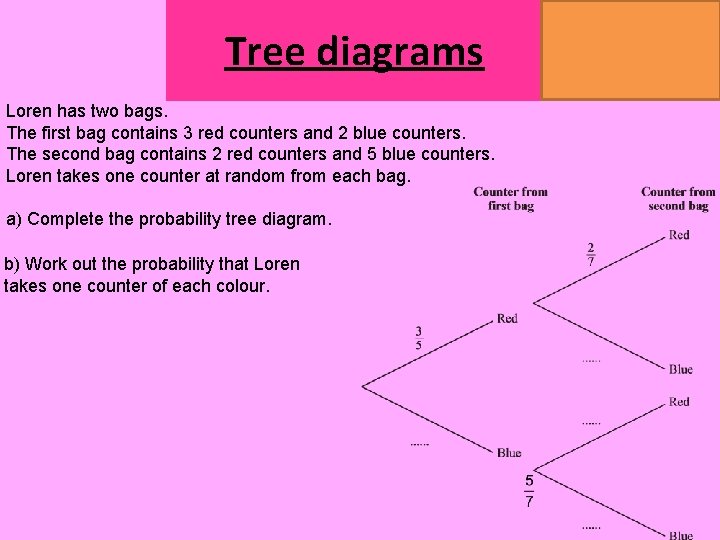
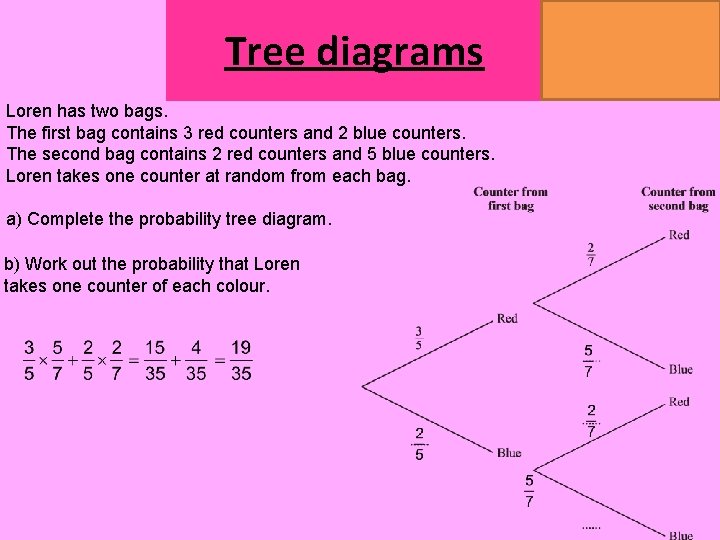
Tree diagrams Loren has two bags. The first bag contains 3 red counters and 2 blue counters. The second bag contains 2 red counters and 5 blue counters. Loren takes one counter at random from each bag. a) Complete the probability tree diagram. b) Work out the probability that Loren takes one counter of each colour. MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7

Tree diagrams Loren has two bags. The first bag contains 3 red counters and 2 blue counters. The second bag contains 2 red counters and 5 blue counters. Loren takes one counter at random from each bag. a) Complete the probability tree diagram. b) Work out the probability that Loren takes one counter of each colour. MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Tree diagrams § Each time the tree splits, the probabilities of those branches need to add up to 1 § To answer questions from the tree diagram Ø Decide which “routes” will solve the problem Ø MULTIPLY the probabilities along the branches as you follow each route, writing the answer at the end of that route Ø ADD together the probabilities of the correct routes

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 NON-REPLACEMENT

Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Non-replacement questions § Sometimes you will not want to replace the item before making the second selection § For example Ø Choosing items of food or drink – you will not be putting it back as it will be consumed! Ø Choosing a pair of socks – once you choose the first sock you will keep it to wear, not put it back Ø Choosing two people from a group to help you with a job – once the first person is chosen the group you are selecting from the second time is now different § These questions are about DEPENDENT events

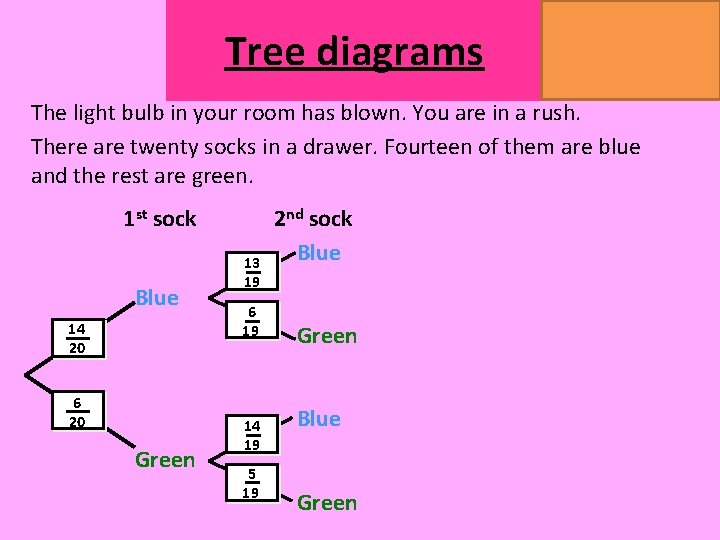
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 The light bulb in your room has blown. You are in a rush. There are twenty socks in a drawer. Fourteen of them are blue and the rest are green. 1 st sock Blue 14 20 6 20 Green 13 19 6 19 14 19 5 19 2 nd sock Blue Green

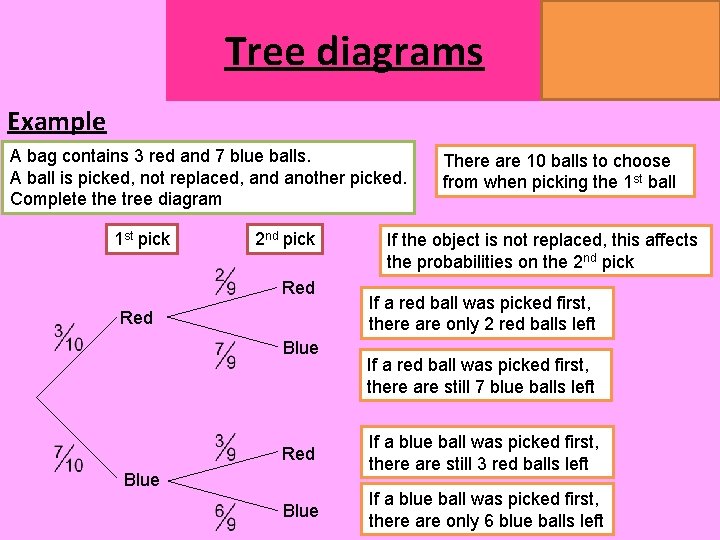
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 Example A bag contains 3 red and 7 blue balls. A ball is picked, not replaced, and another picked. Complete the tree diagram 1 st pick 2 nd pick Red Blue There are 10 balls to choose from when picking the 1 st ball If the object is not replaced, this affects the probabilities on the 2 nd pick If a red ball was picked first, there are only 2 red balls left If a red ball was picked first, there are still 7 blue balls left Red If a blue ball was picked first, there are still 3 red balls left Blue If a blue ball was picked first, there are only 6 blue balls left Blue

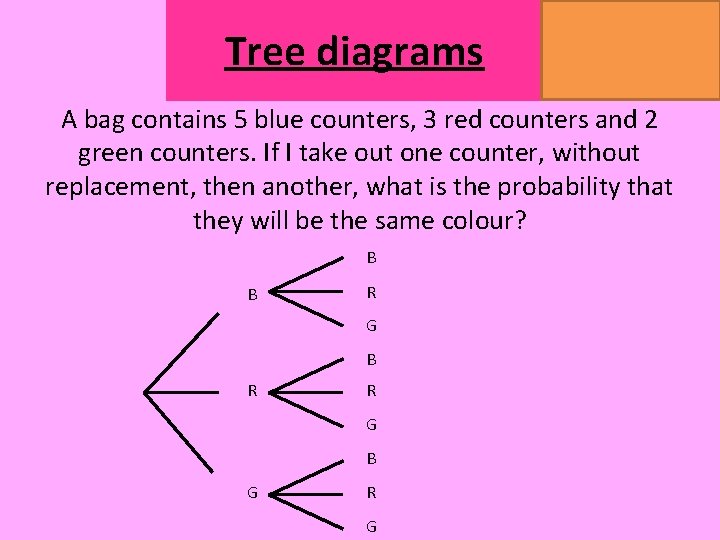
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 A bag contains 5 blue counters, 3 red counters and 2 green counters. If I take out one counter, without replacement, then another, what is the probability that they will be the same colour? B B R G B R R G B G R G

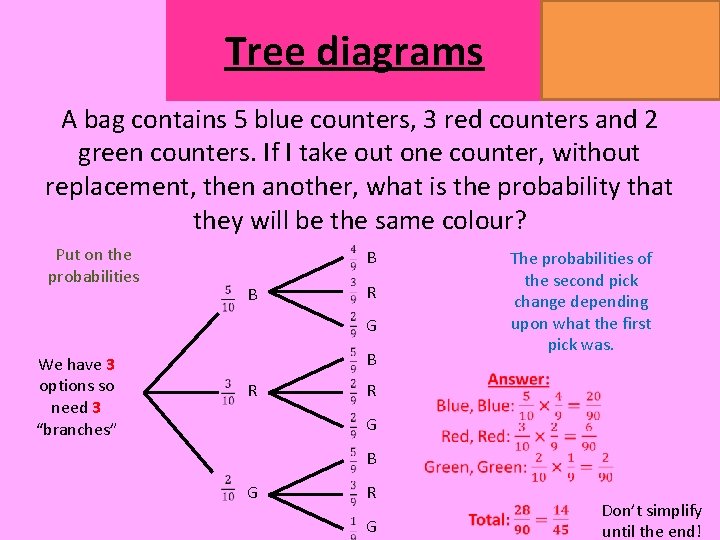
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 A bag contains 5 blue counters, 3 red counters and 2 green counters. If I take out one counter, without replacement, then another, what is the probability that they will be the same colour? Put on the probabilities B B R G We have 3 options so need 3 “branches” B R The probabilities of the second pick change depending upon what the first pick was. R G B G R G Don’t simplify until the end!

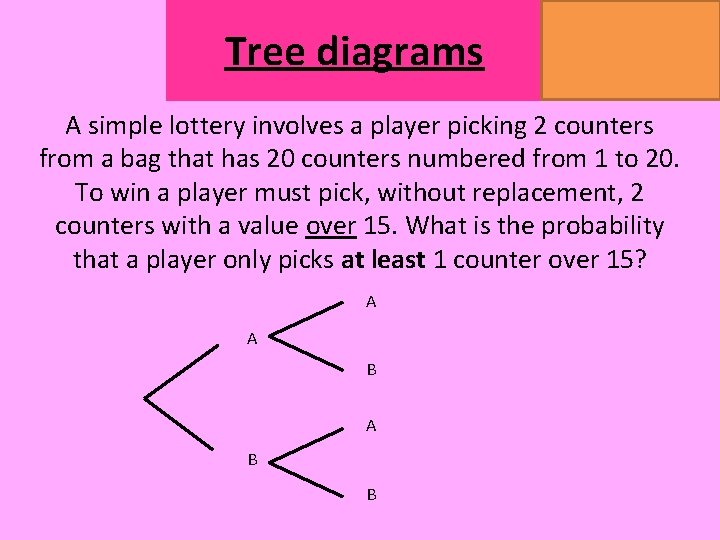
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 A simple lottery involves a player picking 2 counters from a bag that has 20 counters numbered from 1 to 20. To win a player must pick, without replacement, 2 counters with a value over 15. What is the probability that a player only picks at least 1 counter over 15? A A B B

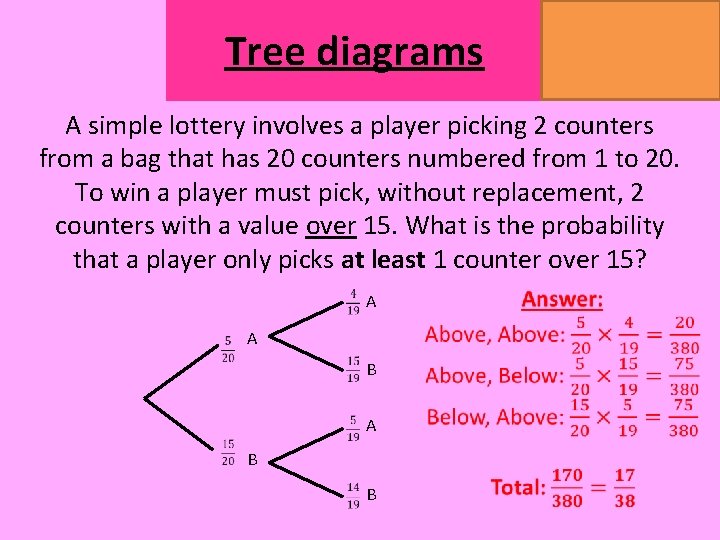
Tree diagrams MATHSWATCH CLIP 151, 175, 204 GRADE 4, 5, 7 A simple lottery involves a player picking 2 counters from a bag that has 20 counters numbered from 1 to 20. To win a player must pick, without replacement, 2 counters with a value over 15. What is the probability that a player only picks at least 1 counter over 15? A A B B