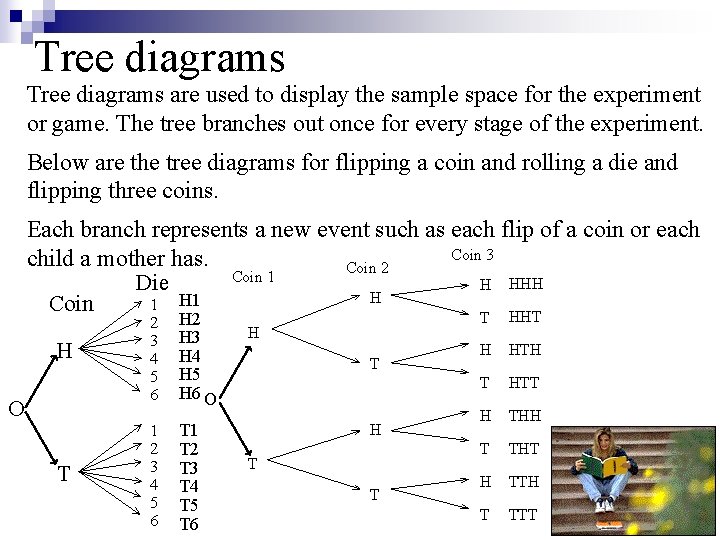
Tree diagrams are used to display the sample

  • Slides: 5
Download presentation
Tree diagrams are used to display the sample space for the experiment or game.

Tree diagrams are used to display the sample space for the experiment or game. The tree branches out once for every stage of the experiment. Below are the tree diagrams for flipping a coin and rolling a die and flipping three coins. Each branch represents a new event such as each flip of a coin or each Coin 3 child a mother has. Coin 2 Coin 1 H HHH Die H 1 Coin T HHT H O T 2 3 4 5 6 H 2 H 3 H 4 H 5 H 6 O 1 2 3 4 5 6 T 1 T 2 T 3 T 4 T 5 T 6 H T T H HTH T HTT H THH T THT H TTH T TTT

Probability tree diagrams With probability tree diagrams you place the probability of each event

Probability tree diagrams With probability tree diagrams you place the probability of each event on each arm of the diagram. If there is no replacement in a question the probabilities on the arms change after each event. Example 1 Note the probabilities on each set of arms adds to 1 DON’T simplify the probabilities. This means all answers will have the same denominators 2 D’s and 8 N’s are placed in a hat. 3 “letters” are drawn WITHOUT replacement. Draw a probability tree to show the outcomes.

Example 2 A hat has 5 red disks and 3 black disks. Two disks

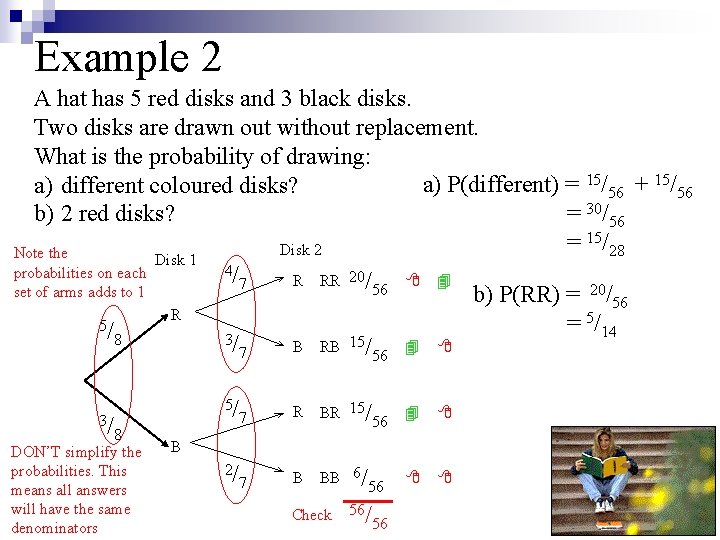
Example 2 A hat has 5 red disks and 3 black disks. Two disks are drawn out without replacement. What is the probability of drawing: a) P(different) = 15/56 + 15/56 a) different coloured disks? = 30/56 b) 2 red disks? 15/ = Disk 2 28 Note the Disk 1 4/ probabilities on each R RR 20/ 7 56 set of arms adds to 1 b) P(RR) = 20/56 R = 5/14 5/ 8 3/ B RB 15/ 7 56 3/ 8 DON’T simplify the probabilities. This means all answers will have the same denominators 5/ 7 R BR 15/ 2/ 7 B BB 6/ 56 B Check 56 56/ 56

Example 3 The probability of a Sydney resident catching the flu is 60%. In

Example 3 The probability of a Sydney resident catching the flu is 60%. In a sample of 3 Sydney residents, what is the probability that; a) exactly 2 residents have the flu? b) at least one resident has the flu? The resident can be either have the flu (F, 3/5) or be healthy (H , 2/5). Resident 1 3/ 5 5 F F 2/ 5 5 H F H 5 H As the population is so large, 125 the probability does not change. F FFF 27/ 5 H FFH 18/ 125 5 F FHF 18/ 125 2/ 5 H 3/ FHH 12/125 5 F HFF 2/ 5 H HFH 12/125 5 F HHF 12/125 5 H HHH 2/ 3/ 2/ Resident 3 5 3/ 3/ 2/ Resident 2 3 / 2/ Check 18/ 8/ 125 125/ 125 a) P(2 F, 1 H) = 18/125 × 3 = 54/125 b) P(≥ 1 F) = 1 − P(3 H) = 1 − 8/125 = 117/125

Today’s work Exercise 6 -07 Page 219 → 220 1 → 4, 7, 9

Today’s work Exercise 6 -07 Page 219 → 220 1 → 4, 7, 9 → 11 & 14 Yesterday’s work Exercise 6 -06 Page 214 → 216 Odds