Tree Automata First A reminder on Automata on

Tree Automata First: A reminder on Automata on words Typing semistructured data

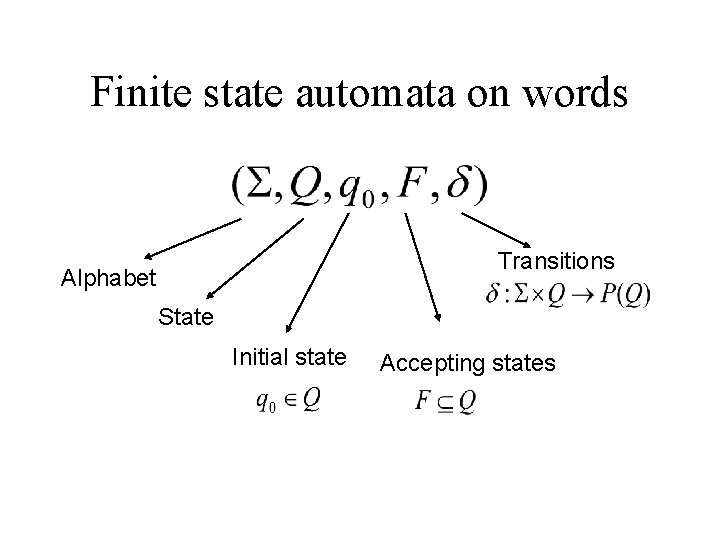
Finite state automata on words Transitions Alphabet State Initial state Accepting states Typing semistructured data

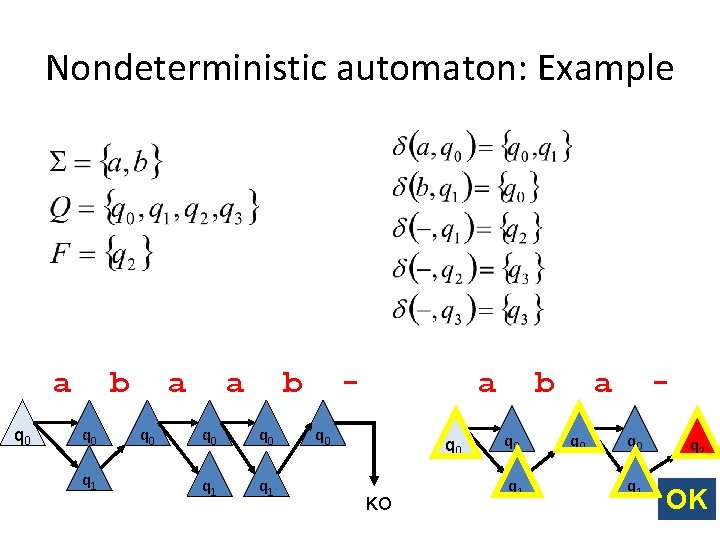
Nondeterministic automaton: Example a q 0 b q 0 q 1 a q 0 a b q 0 q 1 a q 0 KO b q 0 q 1 a q 0 q 1 q 2 OK

Reminder • Deterministic – No transition – No alternative transitions such as • Determinization – It is possible to obtain an equivalent deterministic automaton – State of new automaton = set of states of the original one – Possible exponential blow-up • Minimization • Limitations – cannot do – Context-free languages • Essential tool – e. g. , lexical analysis

(Reminder (2 • • L(A) = set of words accepted by automata A Regular languages Can be described by regular expressions, e. g. a(b+c)*d Closed under complement • Closed under union, intersection – Product automata with states (s, s’) where s is from A and s’ is from A’

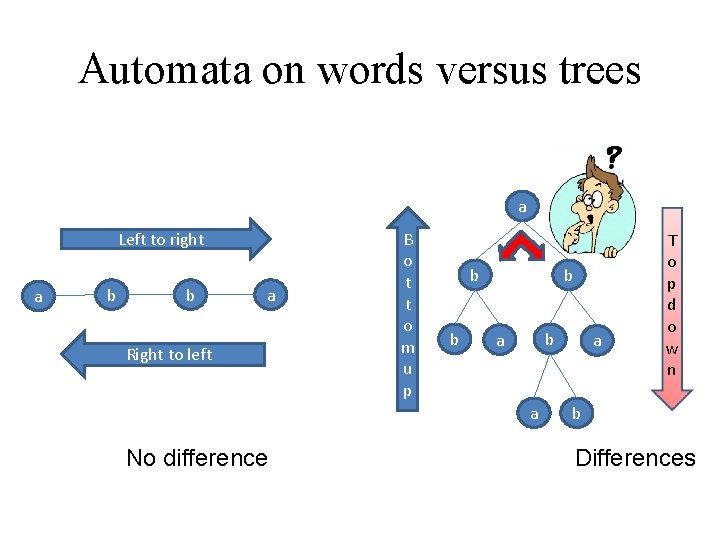
Automata on words versus trees a Left to right a b b a Right to left B o t t o m u p b b a a No difference a T o p d o w n b Differences

Automata on ranked trees Typing semistructured data

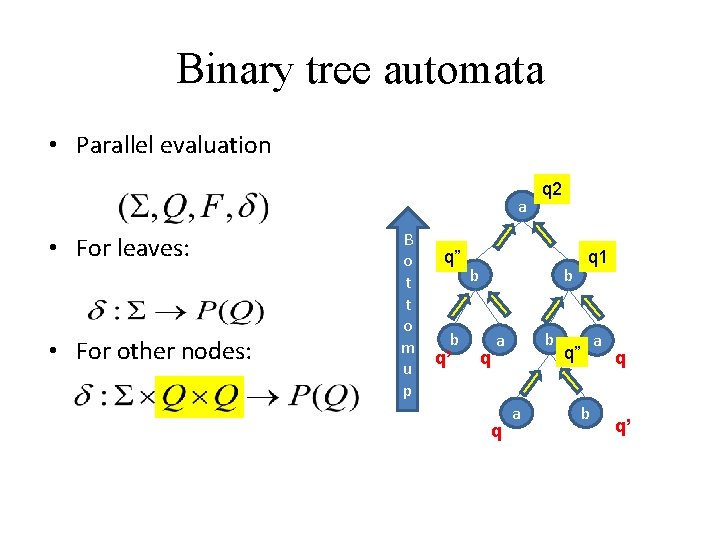
Binary tree automata • Parallel evaluation a • For leaves: • For other nodes: B o t t o m u p q” b q’ b b q b a q Typing semistructured data q 2 a q 1 a q” b q q’

Bottom-up tree automata • Bottom-up: if a node labeled a has its children in states q, q’ then the node moves nondeterministically to state r or r’ • Accepts is the root is in some state in F • Not deterministic if alternatives or -transitions:

Example: deterministic bottom-up

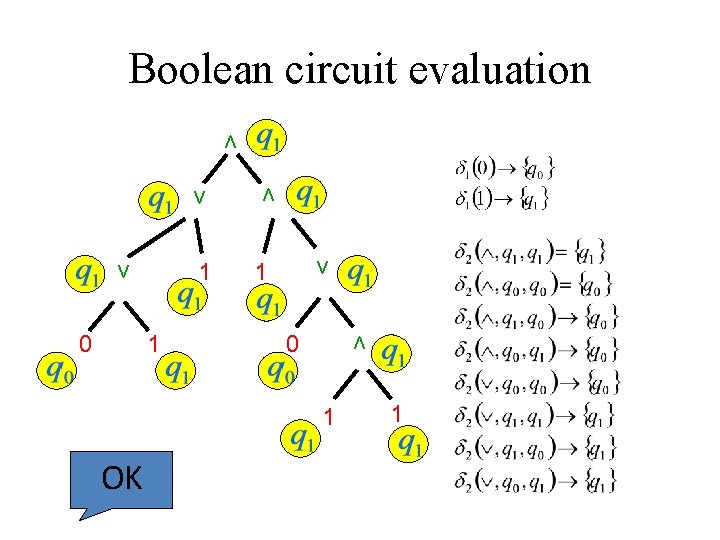
Boolean circuit evaluation v 1 1 v 0 v 1 0 v v v 1 OK 1

Regular tree language = set of trees accepted by a bottom-up tree automaton Typing semistructured data

Regular tree languages Theorem: the following are equivalent – L is a regular tree language – L is accepted by a nondeterministic bottom-up automaton – L is accepted by a nondeterministic top-down automaton Deterministic top-down is weaker

Top-down tree automata • Top-down: if a node labeled a is in state q”, then its left child moves to state q, right to q’ • Accepts is all leaves are in states in F • Not deterministic if

Why deterministic top-down is weaker? • Consider the language – L = { <r> <a>, <b> <r>, <r> <b>, <a><r>) } • It can be accepted by a bottom-up TA – Exercise: write a BUTA A such that L = L(A) • Suppose that B is a deterministic top-down TA that accepts both trees in L – Exercise: Show that B also accepts <r> <a> <r> – A contradiction Fact: No deterministic top-down tree automata accepts exactly L

Ranked trees automata: Properties • • Like for words Determinization Minimization Closed under – Complement – Intersection – Union

…But • XML documents are unranked: book (intro, section*, conclusion)

Automata on unranked tree Typing semistructured data

Unranked tree automata Issue: represent an infinite set of transitions Solution: a regular language

(Unranked tree automata (2 • Rule: • Meaning: if the states of the children of some node labeled a form a word in L(Q), this node moves to some state in {r 1, …, rm}

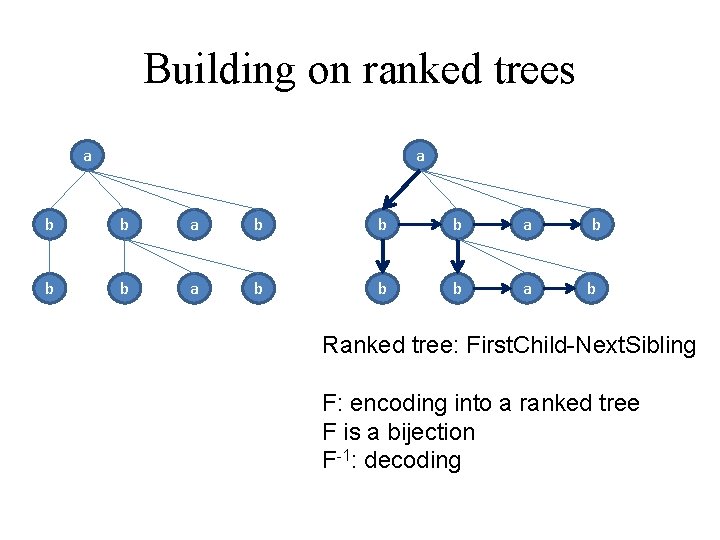
Building on ranked trees a a b b b a b b Ranked tree: First. Child-Next. Sibling F: encoding into a ranked tree F is a bijection F-1: decoding

Building on bottom-up ranked trees (2) • For each Unranked TA A, there is a Ranked TA accepting F(L(A)) • For each Ranked TA A, there is an unranked TA accepting F-1(L(A)) • Both are easy to construct Consequence: Unranked TA are closed under union, intersection, complement Determinaztaion also possible, a bit more tricky