Tree Analysis Solution of recurrence by tree analysis

Tree Analysis

Solution of recurrence by tree analysis Substitution method requires guess of the solution Tree analysis does not require a guess If tree analysis give an approximate solution, verify result by substitution method
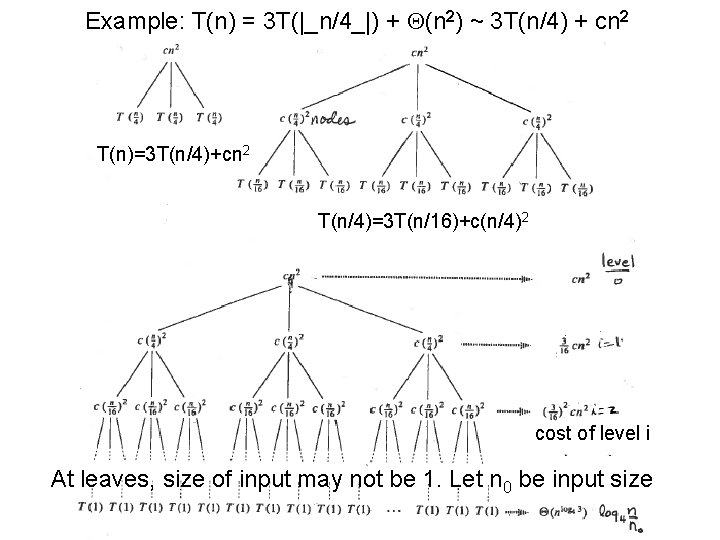
Example: T(n) = 3 T(|_n/4_|) + Q(n 2) ~ 3 T(n/4) + cn 2 T(n)=3 T(n/4)+cn 2 T(n/4)=3 T(n/16)+c(n/4)2 cost of level i At leaves, size of input may not be 1. Let n 0 be input size

Required steps in structured solutions of recurrence relations by tree analysis Draw sufficient branches to determine cost of level i Calculate “istop” with allowance for leaves with n>1 Cost of leaves = constant times number of leaves Cost of levels = S i=0 to istop-1 cost level i Solution in asymptotic notation for dominate term
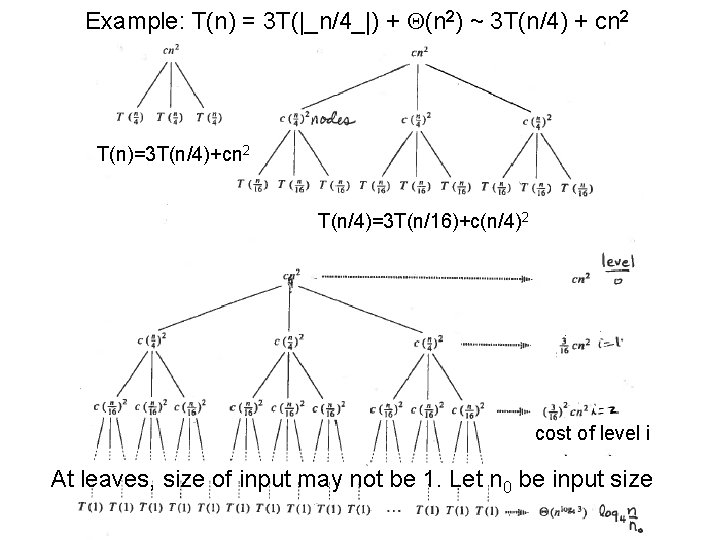
Example: T(n) = 3 T(|_n/4_|) + Q(n 2) ~ 3 T(n/4) + cn 2 T(n)=3 T(n/4)+cn 2 T(n/4)=3 T(n/16)+c(n/4)2 cost of level i At leaves, size of input may not be 1. Let n 0 be input size


ISTOP is the index of leaves. At ISTOP divide and conquer has bottomed out with subgroups of size n 0 As indicated in previous slide, levels are indexed from zero to ISTOP-1 series Bounding by infinite series easier but result requires testing by the substitution method. Guess

Evaluate cost of level using the finite geometric sum. << Q(n 2) Since this sum -> 16/13 at large n, total cost -> 16 cn 2/13; hence T(n)=Q(n 2)

Assignment 9 Use a structured tree analysis to informally prove that T(n) = 4 T(floor(n/2)) + cn c>0 has asymptotic solution T(n) = Q(n 2)
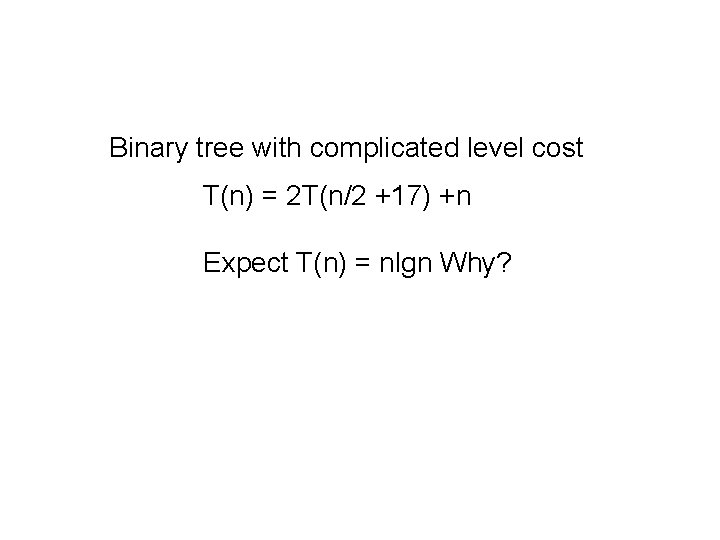
Binary tree with complicated level cost T(n) = 2 T(n/2 +17) +n Expect T(n) = nlgn Why?

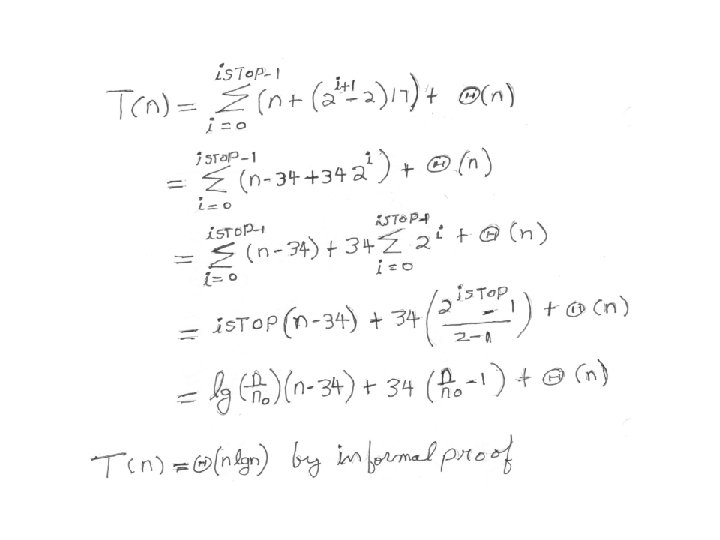
- Slides: 12