Tree 1 KMITL 01076249 Data Structures Algorithms Tree

Tree 1 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 11

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 12

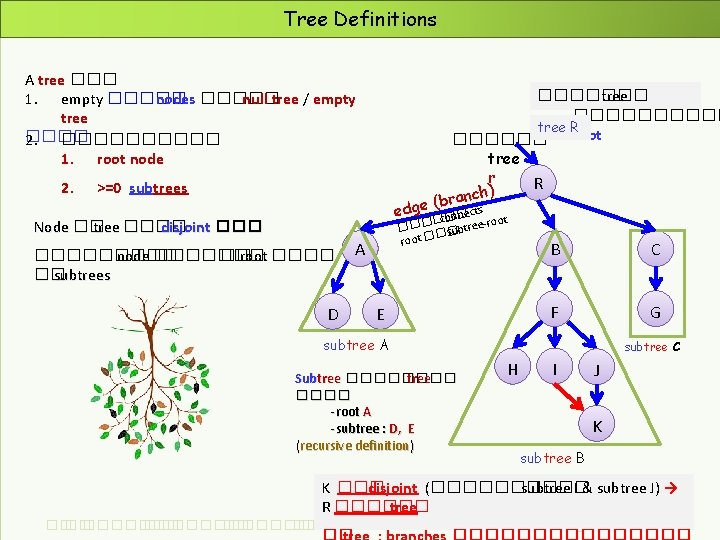
Tree Definitions A tree ��� 1. empty ����� nodes ����� null tree / empty tree ���� 2. ����� 1. root node 2. ������� tree R root ������ tree r R anch) >=0 subtrees (br cts edge �c� ne on� ot ��� s� tree-ro b u � root � Node �� tree ���� disjoint ��������� node ������� �� root ���� �� subtrees D A E B C F G subtree A Subtree ���� -root A -subtree : D, E (recursive definition) subtree C H I J K subtree B K ��� disjoint (����� subtree I & subtree J) → R ������ tree ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 13

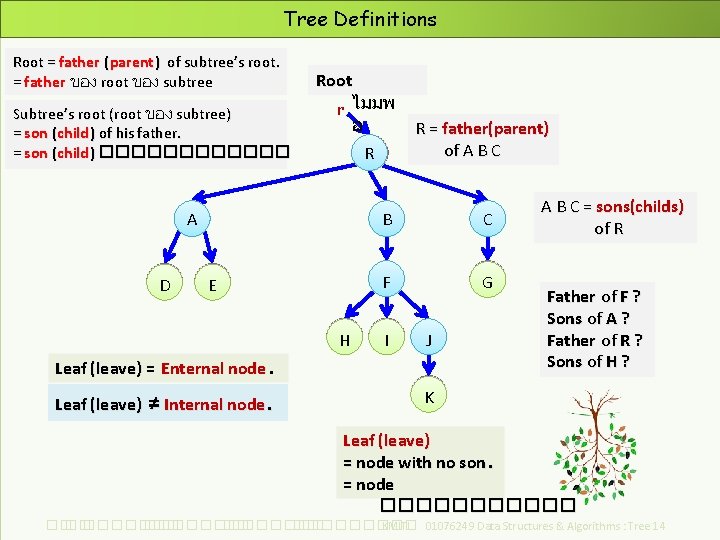
Tree Definitions Root = father (parent ) of subtree’s root. = father ของ root ของ subtree Subtree’s root (root ของ subtree) ( = son (child ) of his father. = son (child ) ������ Root r ไมมพ อ R A D E H R = father(parent) of A B C F G I J Leaf (leave) = Enternal node. Leaf (leave) ≠ Internal node. A B C = sons(childs) of R Father of F ? Sons of A ? Father of R ? Sons of H ? K Leaf (leave) = node with no son. = node ������ ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 14

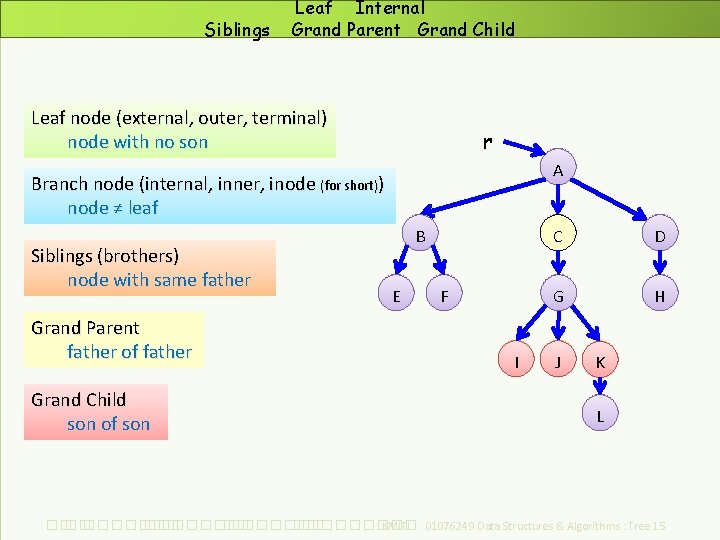
Siblings Leaf Internal Grand Parent Grand Child Leaf node (external, outer, terminal) node with no son r A Branch node (internal, inner, inode (for short)) node ≠ leaf Siblings (brothers) node with same father Grand Parent father of father Grand Child son of son B E F I C D G H J K L ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 15

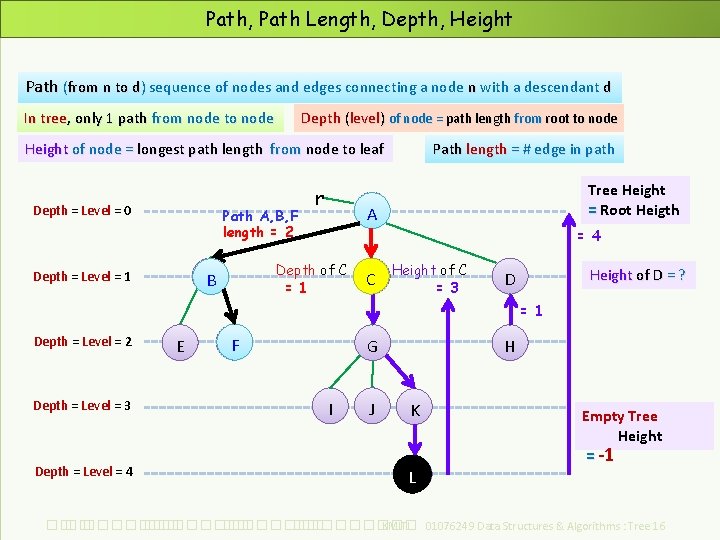
Path, Path Length, Depth, Height Path (from n to d) sequence of nodes and edges connecting a node n with a descendant d In tree, only 1 path from node to node Depth (level) of node = path length from root to node Height of node = longest path length from node to leaf Depth = Level = 0 Path A, B, F length = 2 Depth = Level = 1 r Tree Height = Root Heigth A = 4 Depth of C = 1 B Path length = # edge in path C Height of C = 3 Height of D = ? D = 1 Depth = Level = 2 Depth = Level = 3 Depth = Level = 4 E F H G I J K L Empty Tree Height = -1 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 16

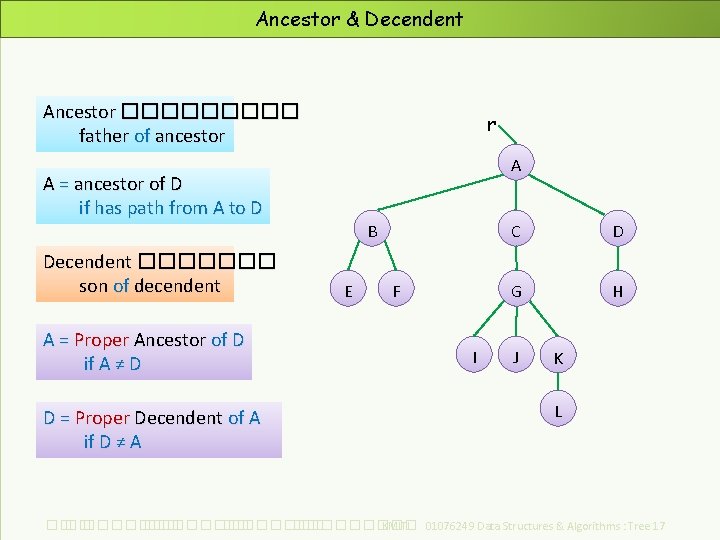
Ancestor & Decendent Ancestor ����� father of ancestor r A A = ancestor of D if has path from A to D Decendent ������� son of decendent A = Proper Ancestor of D if A ≠ D D = Proper Decendent of A if D ≠ A B E F I C D G H J K L ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 17

Tree Examples ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 18

Tree Examples ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 19

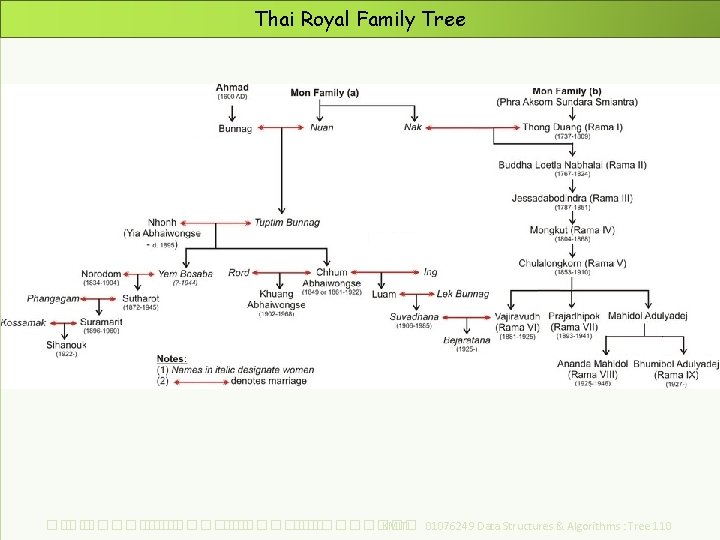
Thai Royal Family Tree ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 110

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 111

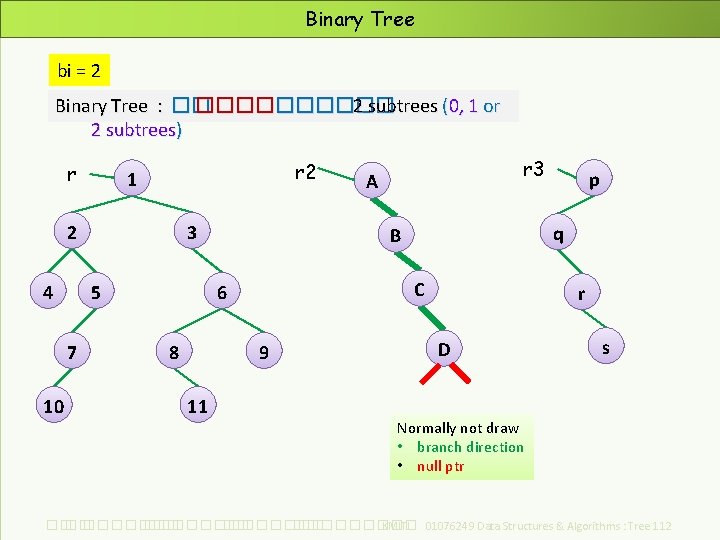
Binary Tree bi = 2 Binary Tree : �� ������ 2 subtrees (0, 1 or 2 subtrees) r r 2 1 2 4 5 7 10 3 C 9 11 p q B 6 8 r 3 A r D s Normally not draw • branch direction • null ptr ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 112

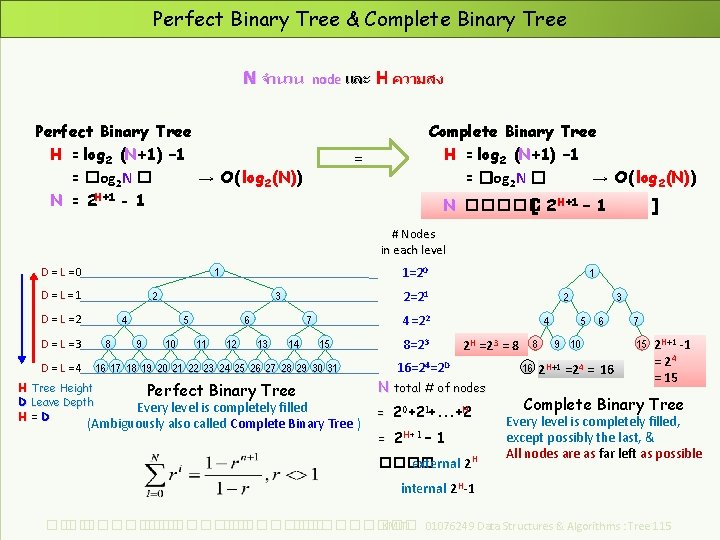
Perfect Binary Tree (Ambiguously also called Complete Binary Tree ) Every level is completely filled # Nodes in each level : Depth = Level = 0 D=L=1 2 D=L=3 1=2 0 1 4 8 5 9 2=2 1 3 10 6 11 12 4=2 2 7 13 14 15 D = L = 4 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 N = จำนวน node ใน perfect binary tree N = 2 0+2 1+. . . +2 H N = 2 H+1 - 1 H = D = log 2 (N+1) – 1 O( log 2(N)) 8=2 3 H Tree Height D Leave Depth H=D 16=2 4=2 D Perfect Binary Tree of N nodes height H : H = log 2 (N+1) – 1 N = 2 H+1 - 1 N = (2 Hexternal ) + (2 H-1 internal ) ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 113

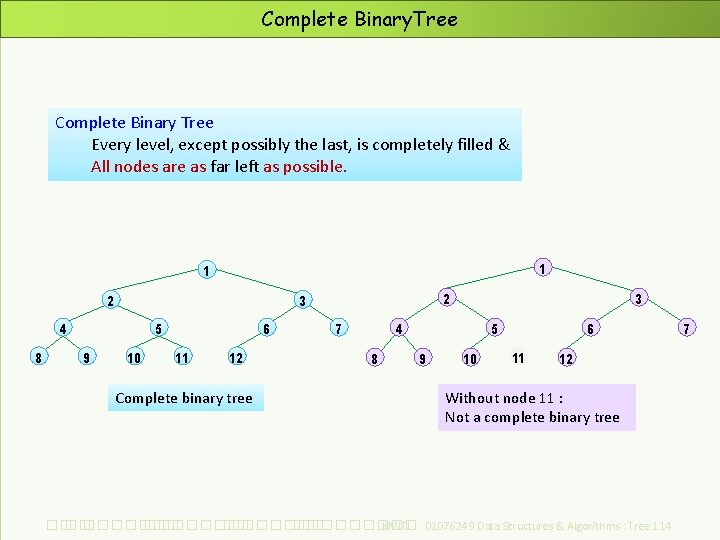
Complete Binary. Tree Complete Binary Tree Every level, except possibly the last, is completely filled & All nodes are as far left as possible. 1 1 2 4 8 5 9 2 3 10 6 11 12 Complete binary tree 3 4 7 8 5 9 10 6 11 12 Without node 11 : Not a complete binary tree ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 114 7

Perfect Binary Tree & Complete Binary Tree N จำนวน node และ Perfect Binary Tree H = log 2 (N+1) – 1 = �log 2 N � → O( log 2(N)) N = 2 H+1 - 1 H ความสง Complete Binary Tree H = log 2 (N+1) – 1 = �log 2 N � → O( log 2(N)) = H, H+1 – 1 N ������� [22 ] # Nodes in each level D=L=0 1=20 1 D=L=1 2 D=L=3 8 D=L=4 5 9 2=21 3 4 10 6 11 12 14 8=23 15 Perfect Binary Tree Every level is completely filled (Ambiguously also called Complete Binary Tree ) 4 2 H =23 = 8 16=24=2 D 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 H Tree Height D Leave Depth H=D 2 4=22 7 13 1 N total # of nodes H = 20+21+. . . +2 = 2 H+1 – 1 ���� external 2 H 8 16 3 5 6 9 10 2 H+1 =24 = 16 7 15 2 H+1 -1 = 24 = 15 Complete Binary Tree Every level is completely filled, except possibly the last, & All nodes are as far left as possible internal 2 H-1 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 115

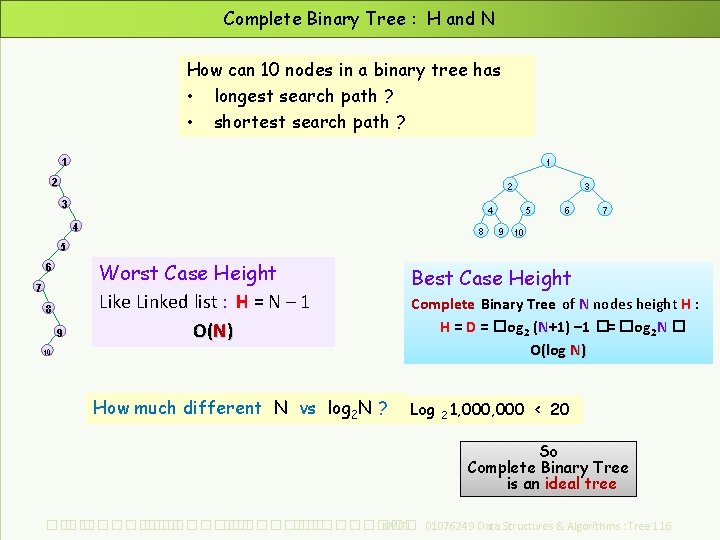
Complete Binary Tree : H and N How can 10 nodes in a binary tree has • longest search path ? • shortest search path ? 1 1 2 2 3 3 4 4 8 5 9 6 7 10 5 6 7 8 9 Worst Case Height Like Linked list : H = N – 1 O(N) 10 How much different N vs log 2 N ? Best Case Height Complete Binary Tree of N nodes height H : H = D = �log 2 (N+1) – 1 �= �log 2 N � O(log N) Log 2 1, 000 < 20 So Complete Binary Tree is an ideal tree ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 116

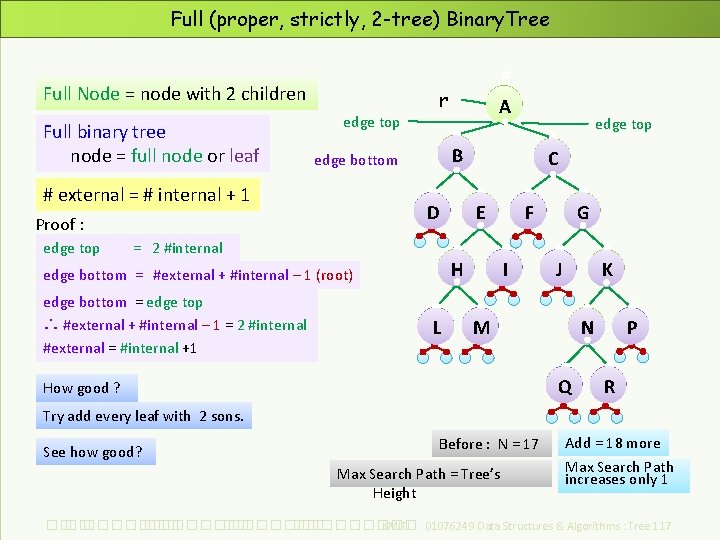
Full (proper, strictly, 2 -tree) Binary. Tree Full Node = node with 2 children Full binary tree node = full node or leaf edge top D Proof : = 2 #internal edge top C E H edge bottom = #external + #internal – 1 (root) edge bottom = edge top ∴ #external + #internal – 1 = 2 #internal #external = #internal +1 A B edge bottom # external = # internal + 1 edge top r L F I G J K M N Q How good ? P R Try add every leaf with 2 sons. See how good? Before : N = 17 Max Search Path = Tree’s Height Add = 18 more Max Search Path increases only 1 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 117

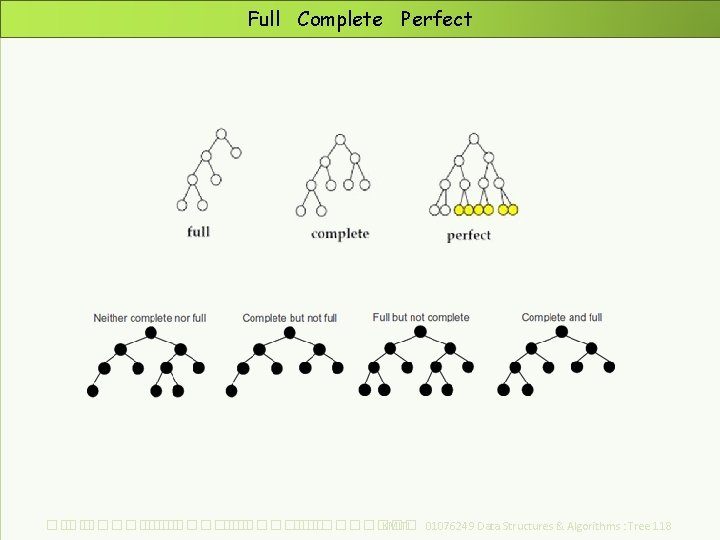
Full Complete Perfect ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 118

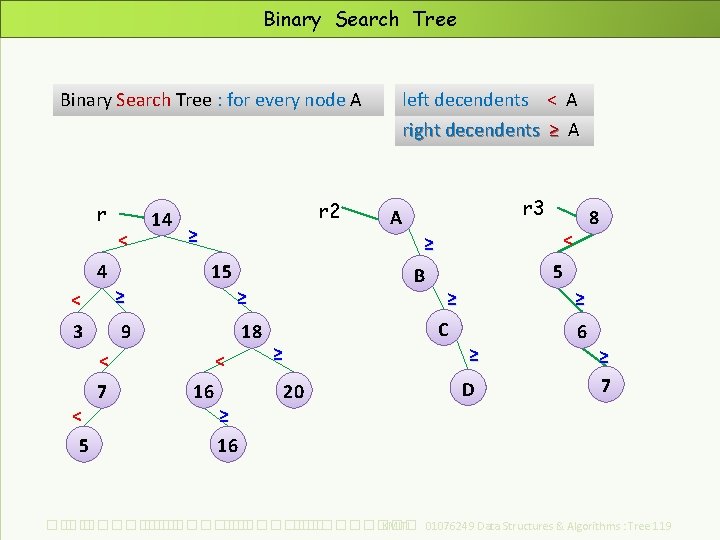
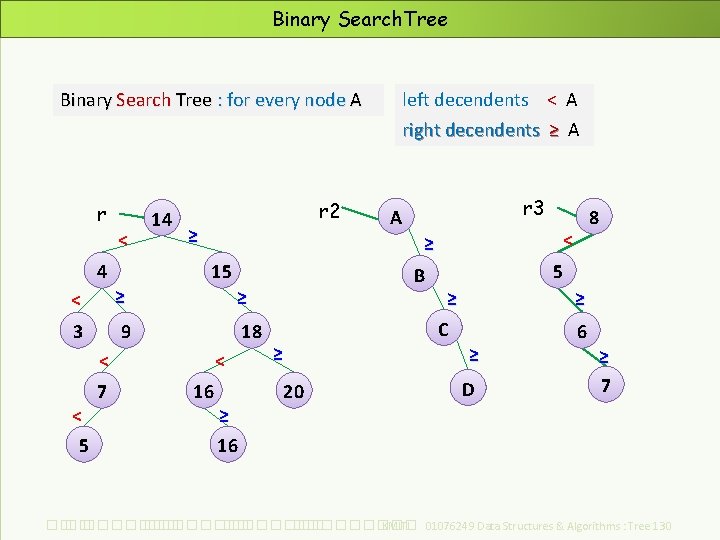
Binary Search Tree : for every node A r < 4 14 r 2 ≥ 15 ≥ ≥ 3 9 18 < < 5 r 3 A < 16 ≥ 16 B ≥ 5 ≥ ≥ C ≥ 20 8 < ≥ < 7 left decendents < A right decendents ≥ A D 6 ≥ 7 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 119

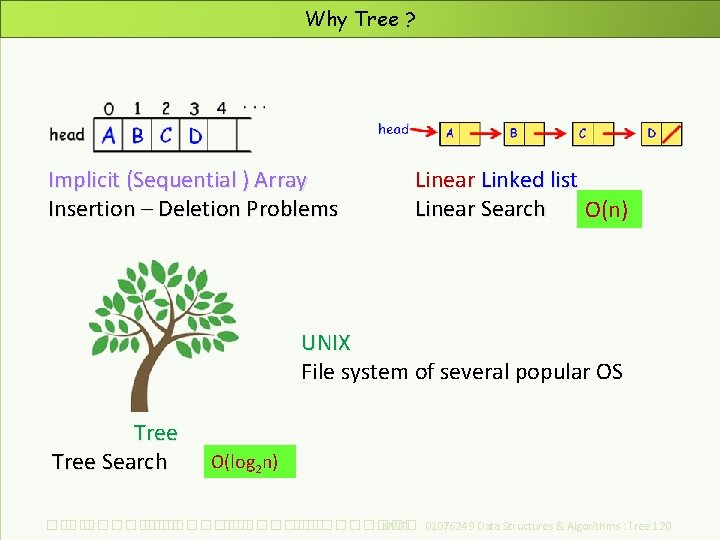
Why Tree ? Implicit (Sequential ) Array Insertion – Deletion Problems Linear Linked list Linear Search O(n) UNIX File system of several popular OS Tree Search O(log 2 n) ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 120

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 121

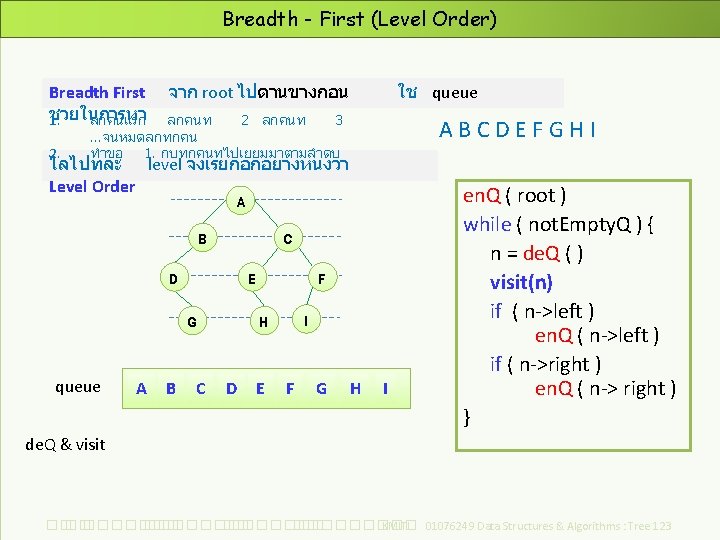
Depth – First Order Depth-First Order ชวยในการหา ไปลกคนแรก จาก root ไปดานลกกอน แบงเปนแลวไปหลานคนแรกกอนไปทลกคนท 3 แบบ ขนกบการวางตำแหนงการ ไวทใด Inorder (Symmetric Order) 1. 2. 3. in. Order(left. Subtree) visit_root in. Order(right. Subtree) ไปดานขาง ใช stack visit 2 root Preorder 1. 2. 3. visit_root pre. Order(left. Subtree) pre. Order(right. Subtree) Postorder 1. 2. 3. post. Order(left. Subtree) post. Order(right. Subtree) visit_root ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 124

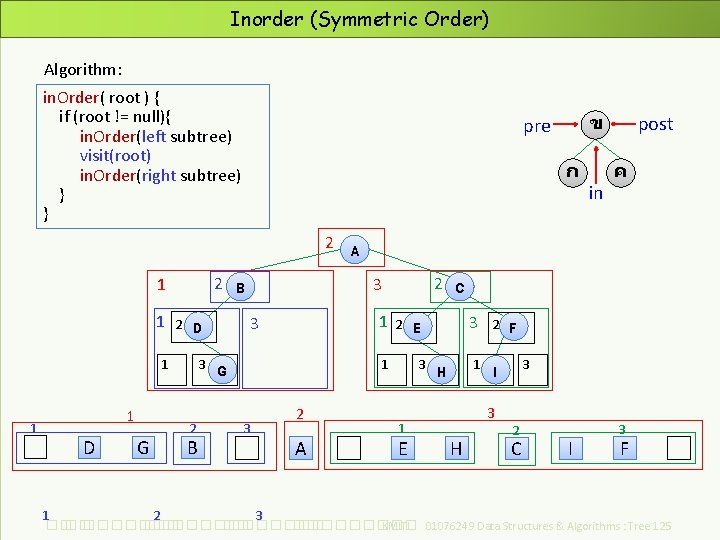
Inorder (Symmetric Order) Algorithm: in. Order( root ) { if (root != null){ in. Order(left subtree) visit(root) in. Order(right subtree) } } ก 2 2 1 1 1 D G 1 2 D 1 3 2 B ข pre 3 G 3 2 A ค A 2 3 B in post 1 2 E 1 3 1 E C H 3 2 F 1 I 3 H 3 2 C I 3 F 2 3 1 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 125

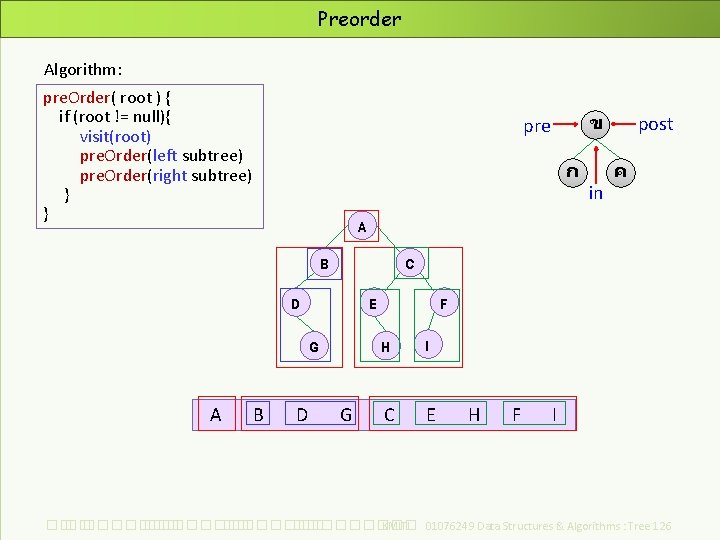
Preorder Algorithm: pre. Order( root ) { if (root != null){ visit(root) pre. Order(left subtree) pre. Order(right subtree) } } ก in post ค A B C D E G A ข pre B D G F H I C E H F I ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 126

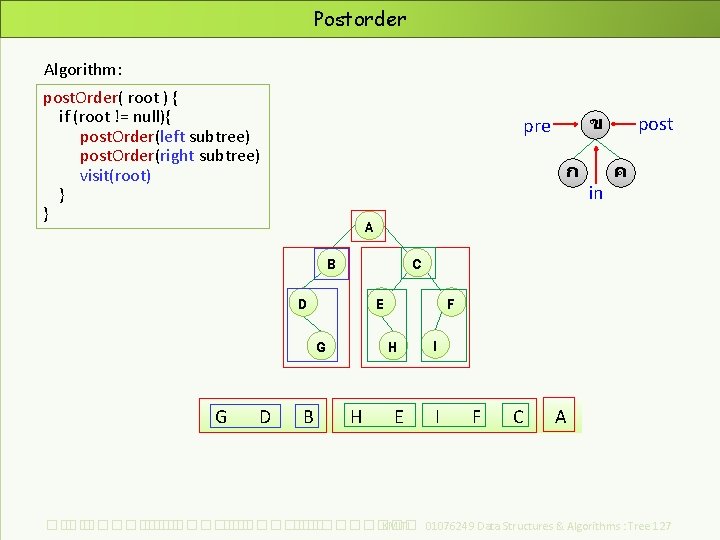
Postorder Algorithm: post. Order( root ) { if (root != null){ post. Order(left subtree) post. Order(right subtree) visit(root) } } ก ค C D E G D in post A B G ข pre B F H H E I I F C A ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 127

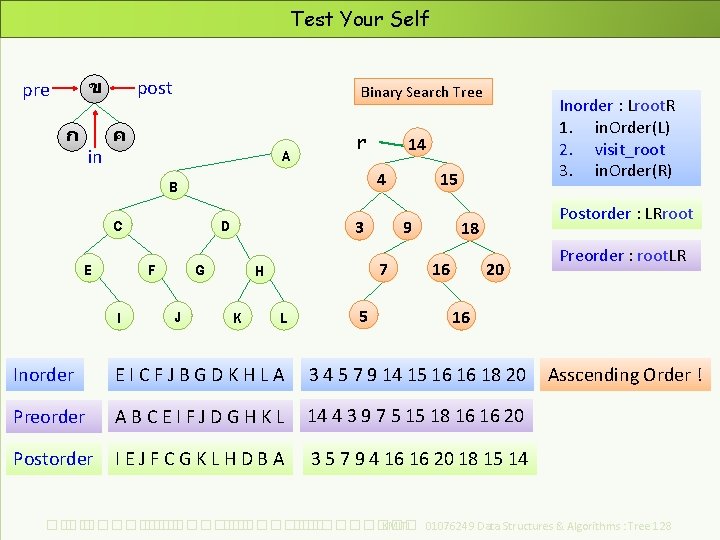
Test Your Self ข pre ก in post Binary Search Tree ค A r C E I 3 D F G J 14 4 B K L 5 15 9 7 H Inorder : Lroot. R 1. in. Order(L) 2. visit_root 3. in. Order(R) Postorder : LRroot 18 16 20 Preorder : root. LR 16 Inorder EICFJBGDKHLA 3 4 5 7 9 14 15 16 16 18 20 Preorder ABCEIFJDGHKL 14 4 3 9 7 5 15 18 16 16 20 Postorder IEJFCGKLHDBA 3 5 7 9 4 16 16 20 18 15 14 Asscending Order ! ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 128

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 129

Binary Search. Tree Binary Search Tree : for every node A r < 4 14 r 2 ≥ 15 ≥ ≥ 3 9 18 < < 5 r 3 A < 16 ≥ 16 B ≥ 5 ≥ ≥ C ≥ 20 8 < ≥ < 7 left decendents < A right decendents ≥ A D 6 ≥ 7 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 130

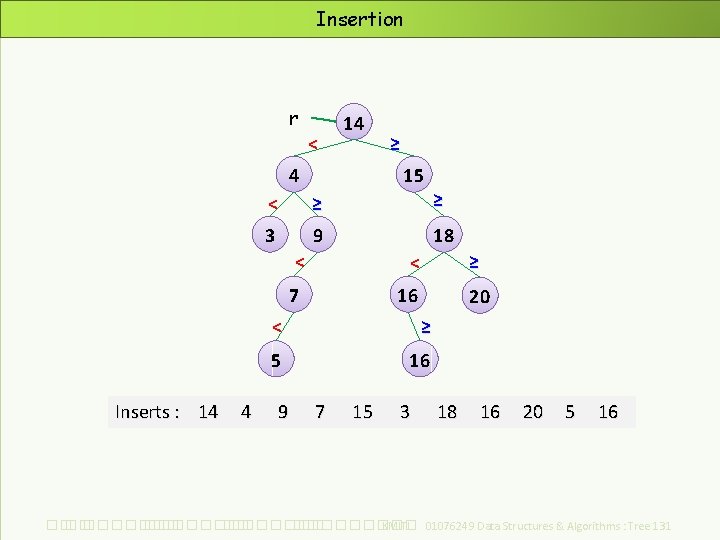
Insertion r < 14 4 Inserts : 14 4 ≥ 15 < ≥ ≥ 3 9 18 < < 7 16 ≥ 20 < ≥ 5 16 9 7 15 3 18 16 20 5 16 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 131

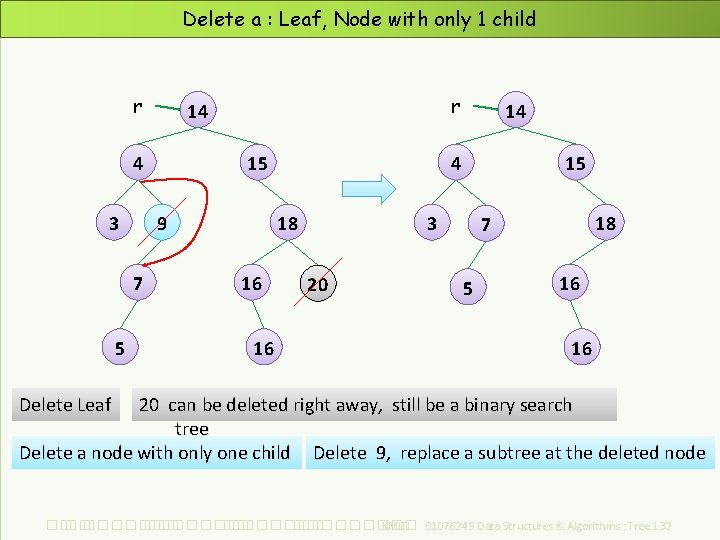
Delete a : Leaf, Node with only 1 child r 4 3 15 9 7 5 r 14 4 18 16 16 14 15 3 20 18 7 5 16 16 Delete Leaf 20 can be deleted right away, still be a binary search tree Delete a node with only one child Delete 9, replace a subtree at the deleted node ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 132

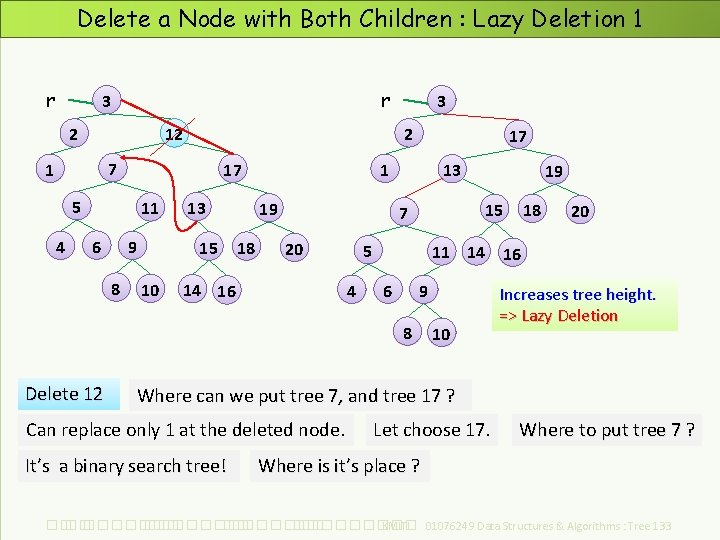
Delete a Node with Both Children : Lazy Deletion 1 r r 3 2 2 12 7 1 17 5 4 11 6 9 8 13 15 10 3 1 19 18 17 13 15 7 20 14 16 5 4 11 14 6 9 8 Delete 12 19 10 18 20 16 Increases tree height. => Lazy Deletion Where can we put tree 7, and tree 17 ? Can replace only 1 at the deleted node. It’s a binary search tree! Let choose 17. Where to put tree 7 ? Where is it’s place ? ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 133

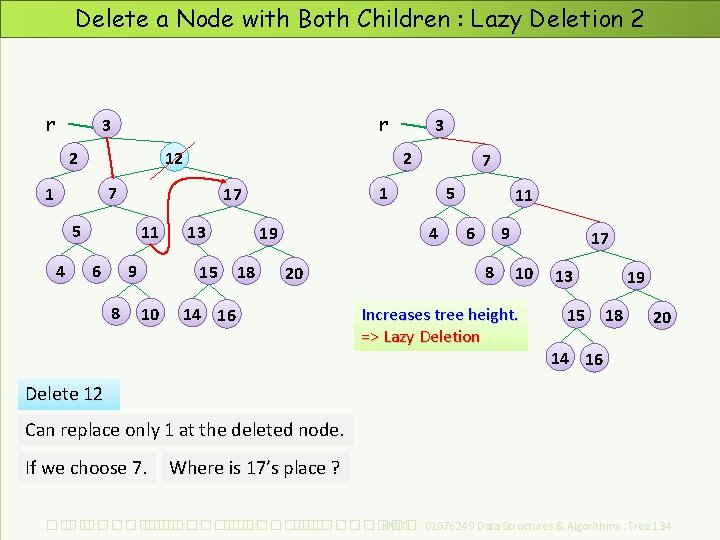
Delete a Node with Both Children : Lazy Deletion 2 r r 3 2 2 12 7 1 4 11 6 9 8 13 15 10 5 4 19 18 7 1 17 5 3 20 14 16 11 6 9 8 17 10 Increases tree height. => Lazy Deletion 13 15 19 18 20 14 16 Delete 12 Can replace only 1 at the deleted node. If we choose 7. Where is 17’s place ? ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 134

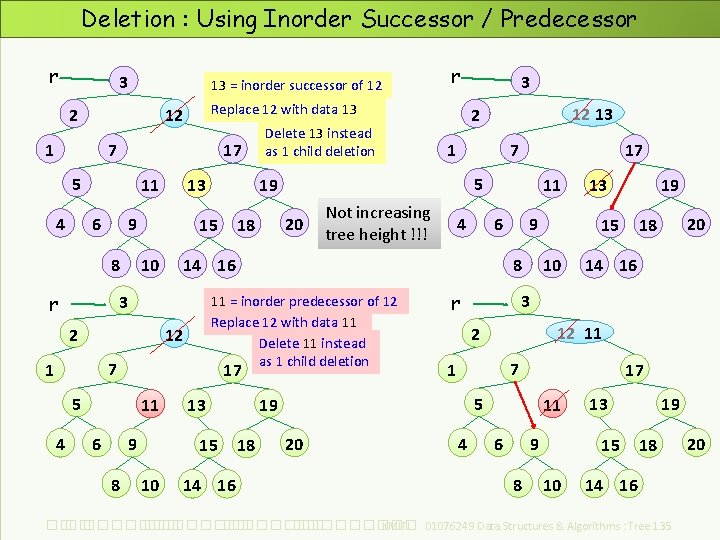
Deletion : Using Inorder Successor / Predecessor r 3 13 = inorder successor of 12 2 Replace 12 with data 13 12 7 1 17 5 6 4 13 11 9 8 r 7 4 11 6 9 8 13 15 10 14 16 17 11 6 4 9 8 17 5 Not increasing tree height !!! 11 = inorder predecessor of 12 Replace 12 with data 11 Delete 11 instead as 1 child deletion 12 1 7 1 5 20 18 12 13 14 16 3 2 Delete 13 instead as 1 child deletion 3 2 19 15 10 r r 14 16 12 11 7 1 4 20 18 3 17 5 20 19 15 10 2 19 18 13 11 6 9 8 13 15 10 19 18 14 16 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 135 20

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 136

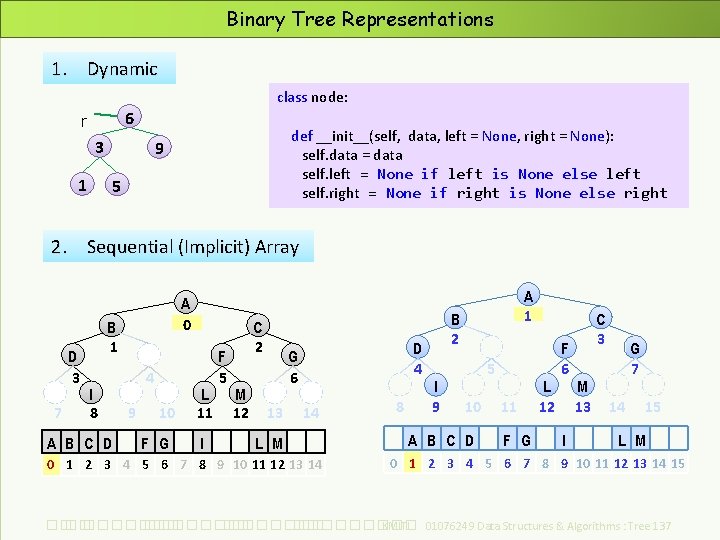
Binary Tree Representations 1. Dynamic class node: 6 r 3 def __init__(self, data, left = None, right = None): self. data = data self. left = None if left is None else left self. right = None if right is None else right 9 1 5 2. Sequential (Implicit) Array D 3 7 A 0 B 1 I 8 A B C D 4 9 10 F G L 11 I F 5 C 2 M 12 D 4 G 6 13 14 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 A 1 B 2 I 9 5 10 A B C D 11 F G L 12 F 6 I C 3 M 13 G 7 14 15 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 137

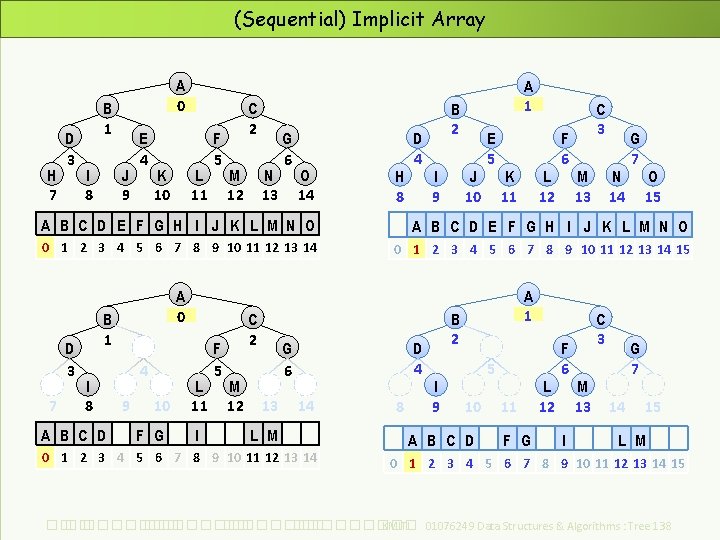
(Sequential) Implicit Array H 7 D 3 A 0 B 1 I 8 J 9 E 4 K 10 L 11 F 5 C 2 M 12 N 13 G 6 O 14 H 8 D 4 A 1 B 2 I 9 J 10 E 5 K 11 L 12 F 6 C 3 M 13 N 14 G 7 O 15 A B C D E F G H I J K L M N O 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D 3 7 A 0 B 1 I 8 A B C D 4 9 10 F G L 11 I F 5 C 2 M 12 G 6 13 D 4 14 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 A 1 B 2 I 9 5 10 A B C D 11 F G L 12 F 6 I C 3 M 13 G 7 14 15 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 138

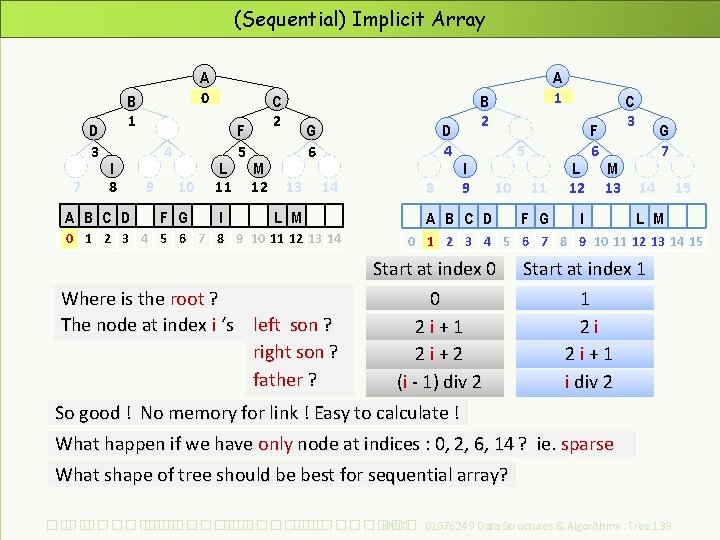
(Sequential) Implicit Array D 3 7 A 0 B 1 I 8 A B C D 4 9 10 F G L 11 I F 5 C 2 M 12 D 4 G 6 13 14 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Where is the root ? The node at index i ‘s left son ? right son ? father ? 8 A 1 B 2 I 9 5 10 A B C D 11 L 12 F G I F 6 C 3 M 13 G 7 14 15 L M 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Start at index 0 0 2 i+1 2 i+2 (i - 1) div 2 Start at index 1 1 2 i 2 i+1 i div 2 So good ! No memory for link ! Easy to calculate ! What happen if we have only node at indices : 0, 2, 6, 14 ? ie. sparse What shape of tree should be best for sequential array? ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 139

Tree 1. Tree Definitions 2. Binary Tree – Traversals – Binary Search Tree – Representations – Application : Expression Tree 3. 4. AVL Tree Which Representions ? 5. n-ary Tree 6. Generic Tree 7. Multiway Search Tree 8. B-Trees ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 140

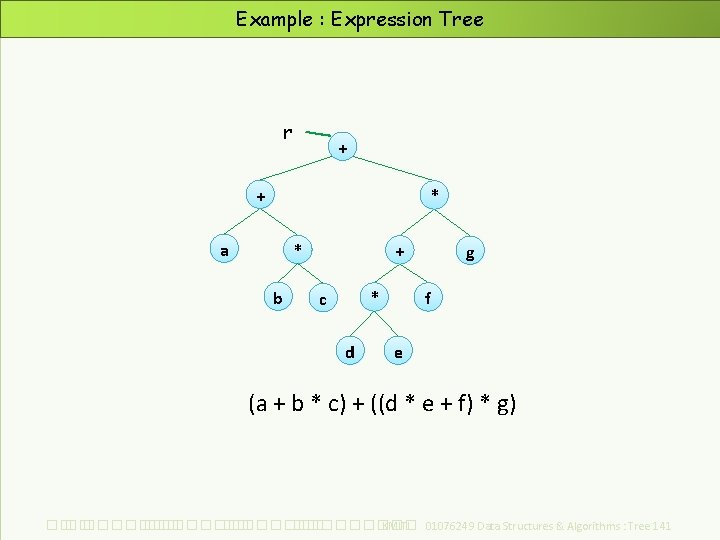
Example : Expression Tree r + + * a * b + * c d g f e (a + b * c) + ((d * e + f) * g) ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 141

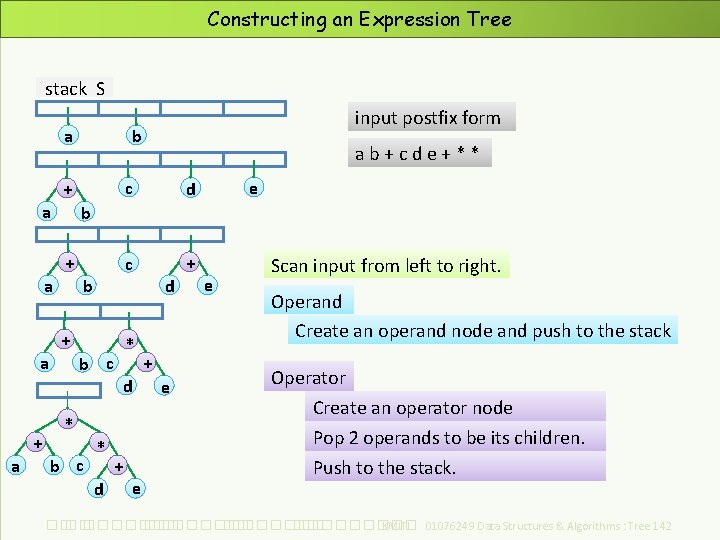
Constructing an Expression Tree stack S a b + a a c d c + d b + * b c a d a ab+cde+** e b + + input postfix form * b c * d + e e Scan input from left to right. Operand Create an operand node and push to the stack Operator Create an operator node Pop 2 operands to be its children. Push to the stack. ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 142

Node class node: def __init__(self, data, left = None, right = None): self. data = data self. left = None if left is None else left self. right = None if right is None else right def __str__(self): return str(self. data) def get. Data(self): return self. data # accessor def get. Left(self): return self. left # accessor def get. Right(self): return self. right # accessor def set. Data(self, data): self. data = data # mutator def set. Left(self, left): self. left = left # mutator def set. Right(self, right): # mutator self. right = right ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 143

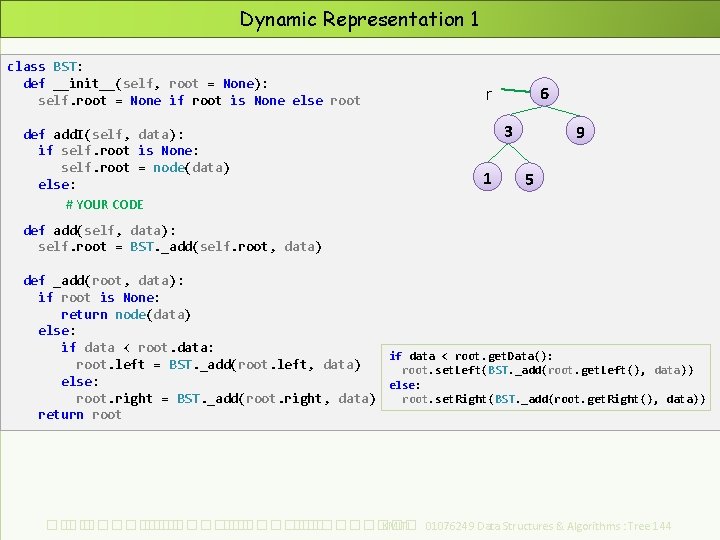
Dynamic Representation 1 class BST: def __init__(self, root = None): self. root = None if root is None else root def add. I(self, data): if self. root is None: self. root = node(data) else: # YOUR CODE r 6 3 1 9 5 def add(self, data): self. root = BST. _add(self. root, data) def _add(root, data): if root is None: return node(data) else: if data < root. data: if data < root. get. Data(): root. left = BST. _add(root. left, data) root. set. Left(BST. _add(root. get. Left(), data)) else: root. right = BST. _add(root. right, data) root. set. Right(BST. _add(root. get. Right(), data)) return root ��. ���������� ��. ��������� KMITL 01076249 Data Structures & Algorithms : Tree 144