TravelingSalesman Problem Ch 6 Hamilton Circuits Euler circuitpath

Traveling-Salesman Problem Ch. 6

Hamilton Circuits • Euler circuit/path => Visit each edge once and only once • Hamilton circuit => Visit each vertex once and only once (except at the end, where it returns to the starting vertex) • Hamilton path => Visit each vertex once and only once • Difference: Edge (Euler) Vertex (Hamilton)

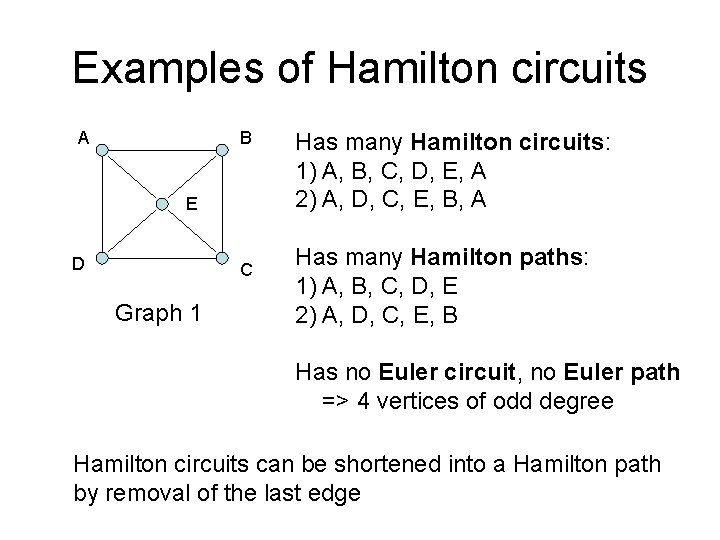
Examples of Hamilton circuits A B E D C Graph 1 Has many Hamilton circuits: 1) A, B, C, D, E, A 2) A, D, C, E, B, A Has many Hamilton paths: 1) A, B, C, D, E 2) A, D, C, E, B Has no Euler circuit, no Euler path => 4 vertices of odd degree Hamilton circuits can be shortened into a Hamilton path by removal of the last edge

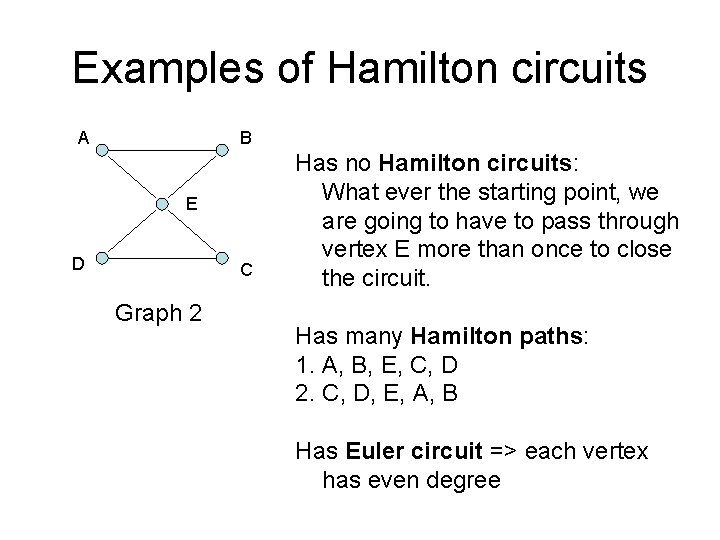
Examples of Hamilton circuits A B E D C Graph 2 Has no Hamilton circuits: What ever the starting point, we are going to have to pass through vertex E more than once to close the circuit. Has many Hamilton paths: 1. A, B, E, C, D 2. C, D, E, A, B Has Euler circuit => each vertex has even degree

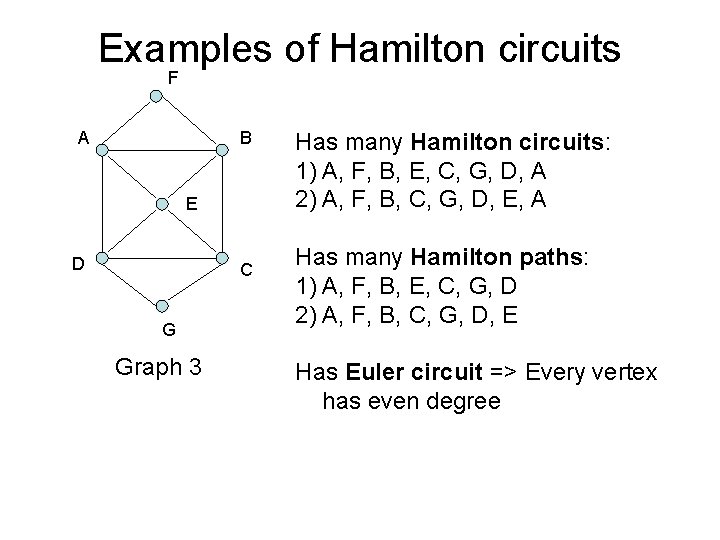
Examples of Hamilton circuits F A B E D C G Graph 3 Has many Hamilton circuits: 1) A, F, B, E, C, G, D, A 2) A, F, B, C, G, D, E, A Has many Hamilton paths: 1) A, F, B, E, C, G, D 2) A, F, B, C, G, D, E Has Euler circuit => Every vertex has even degree

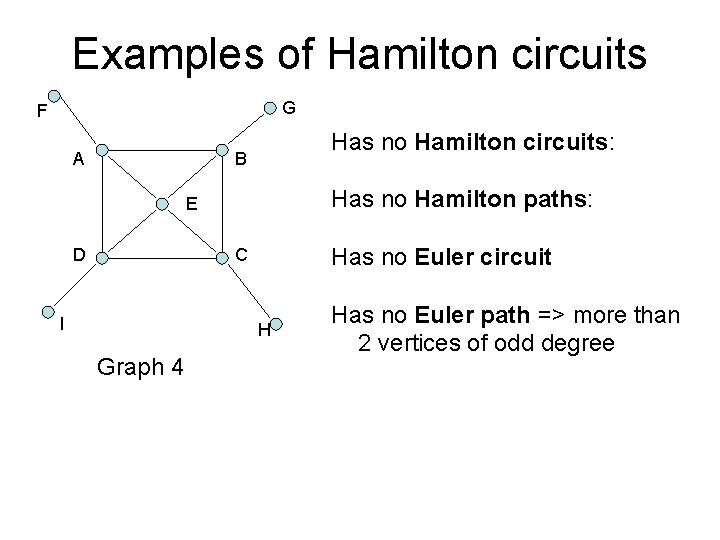
Examples of Hamilton circuits G F A Has no Hamilton circuits: B Has no Hamilton paths: E D Has no Euler circuit C I H Graph 4 Has no Euler path => more than 2 vertices of odd degree

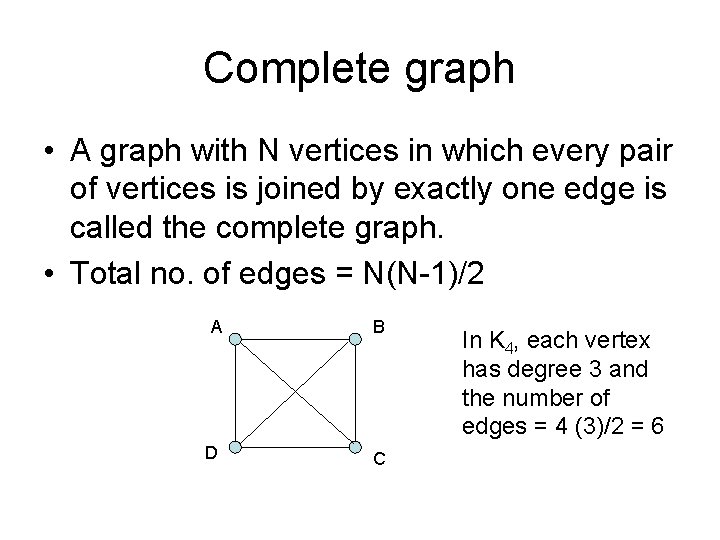
Complete graph • A graph with N vertices in which every pair of vertices is joined by exactly one edge is called the complete graph. • Total no. of edges = N(N-1)/2 A B D C In K 4, each vertex has degree 3 and the number of edges = 4 (3)/2 = 6

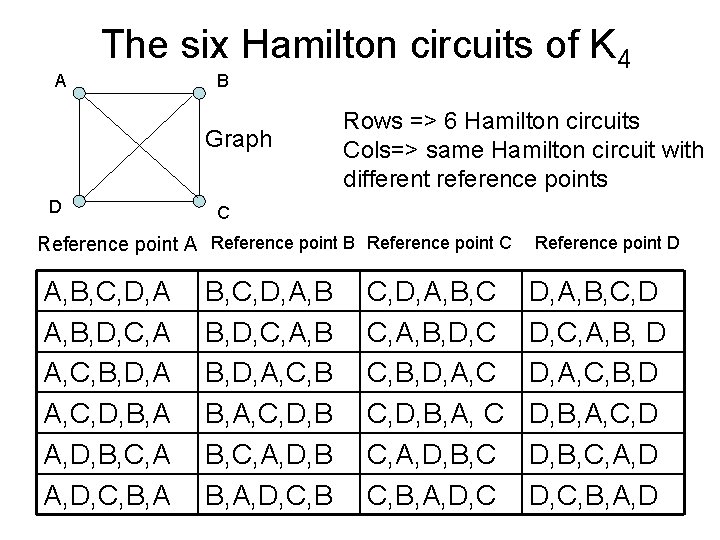
A The six Hamilton circuits of K 4 B Graph D Rows => 6 Hamilton circuits Cols=> same Hamilton circuit with different reference points C Reference point A Reference point B Reference point C A, B, C, D, A A, B, D, C, A A, C, B, D, A A, C, D, B, A A, D, B, C, A A, D, C, B, A B, C, D, A, B B, D, C, A, B B, D, A, C, B B, A, C, D, B B, C, A, D, B B, A, D, C, B C, D, A, B, C C, A, B, D, C C, B, D, A, C C, D, B, A, C C, A, D, B, C C, B, A, D, C Reference point D D, A, B, C, D D, C, A, B, D D, A, C, B, D D, B, A, C, D D, B, C, A, D D, C, B, A, D

Complete graph • The number of Hamilton circuits in a complete graph can be computed by using factorials. • N! (factorial of N) = 1 x 2 x 3 x 4 x … x(N-1)x N • The complete graph with N vertices has (N-1)! Hamilton circuits. • Example: The complete graph with 5 vertices has 4! = 1 x 2 x 3 x 4 = 24 Hamilton circuits

Factorial Which of the following is true? n! = n! x (n-1)! n! = n! + (n-1)! n! = n x (n-1)! n! = n + (n-1)!

No. of edges No of edges in K 10 is • 10! • 90 • 45

Complete graph • • In a complete graph with 14 vertices (A through N), the total number of Hamilton circuits (including mirror-image circuits) that start at vertex A is 14! (14 x 13)/2 15! 13!