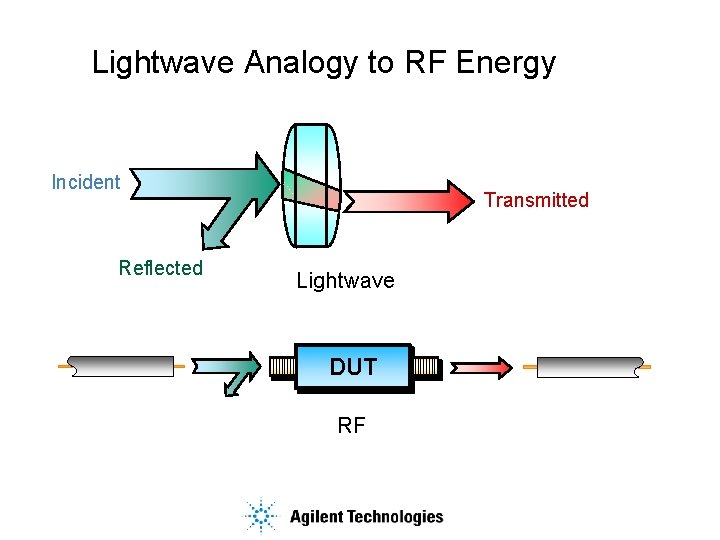
Trasmission lines Lightwave Analogy to RF Energy Incident

Trasmission lines

Lightwave Analogy to RF Energy Incident Reflected Transmitted Lightwave DUT RF

Why Do We Need to Test Components? • Verify specifications of “building blocks” for more complex RF systems • Ensure distortionless transmission of communications signals – linear: constant amplitude, linear phase / constant group delay – nonlinear: harmonics, intermodulation, compression, AM-to -PM conversion • Ensure good match when absorbing power (e. g. , an antenna)

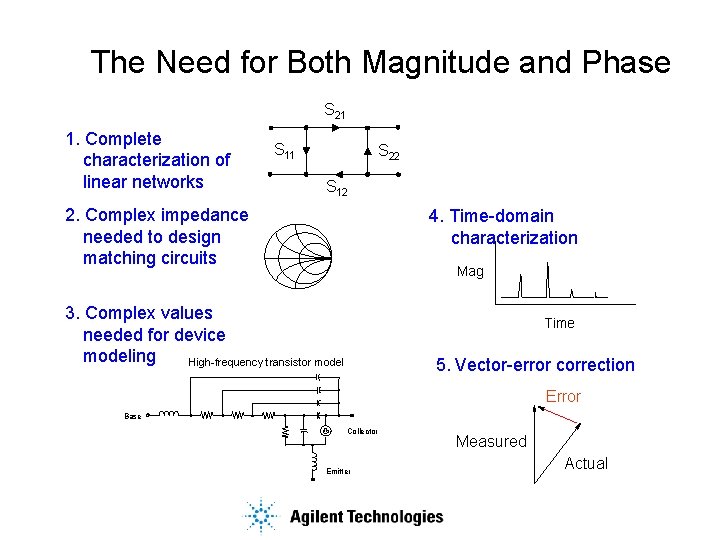
The Need for Both Magnitude and Phase S 21 1. Complete characterization of linear networks S 11 S 22 S 12 2. Complex impedance needed to design matching circuits 4. Time-domain characterization Mag 3. Complex values needed for device modeling High-frequency transistor model Time 5. Vector-error correction Error Base Collector Emitter Measured Actual

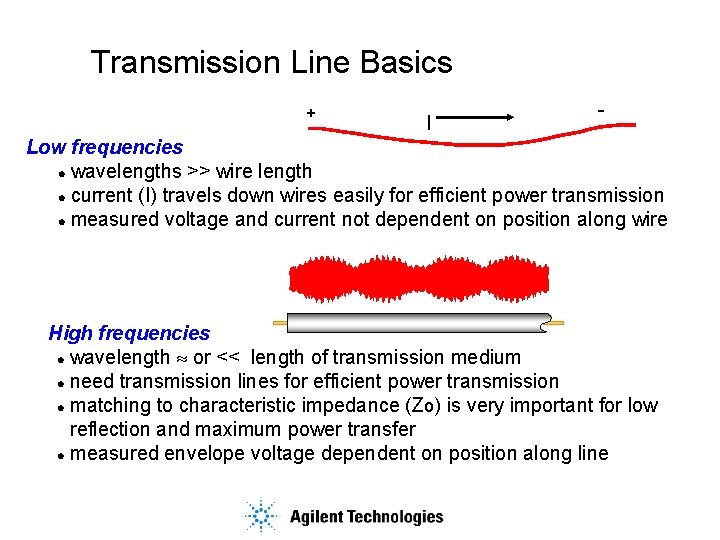
Transmission Line Basics + I - Low frequencies l wavelengths >> wire length l current (I) travels down wires easily for efficient power transmission l measured voltage and current not dependent on position along wire High frequencies l wavelength » or << length of transmission medium l need transmission lines for efficient power transmission l matching to characteristic impedance (Zo) is very important for low reflection and maximum power transfer l measured envelope voltage dependent on position along line

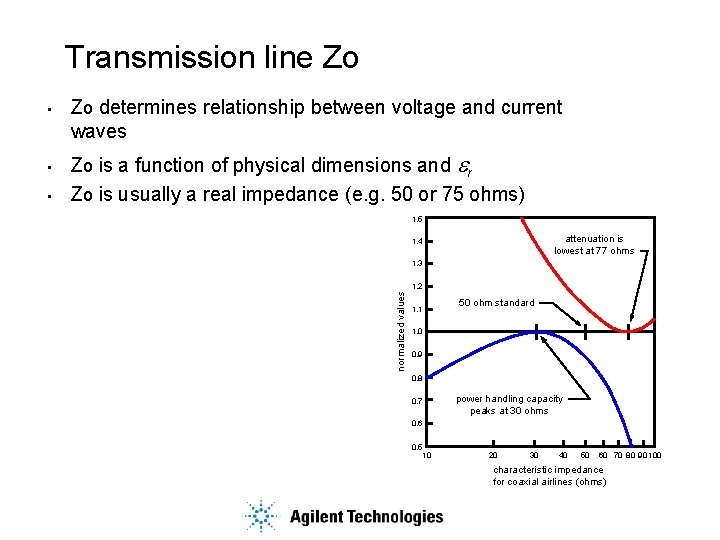
Transmission line Zo • • Zo determines relationship between voltage and current waves Zo is a function of physical dimensions and r Zo is usually a real impedance (e. g. 50 or 75 ohms) 1. 5 attenuation is lowest at 77 ohms 1. 4 1. 3 1. 2 normalized values • 1. 1 50 ohm standard 1. 0 0. 9 0. 8 0. 7 power handling capacity peaks at 30 ohms 0. 6 0. 5 10 20 30 40 50 60 70 80 90 100 characteristic impedance for coaxial airlines (ohms)

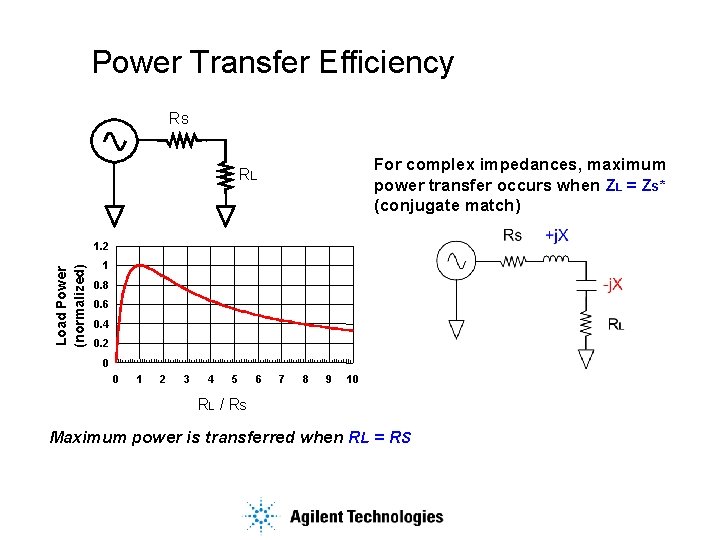
Power Transfer Efficiency RS For complex impedances, maximum power transfer occurs when ZL = ZS* (conjugate match) RL Load Power (normalized) 1. 2 1 0. 8 0. 6 0. 4 0. 2 0 0 1 2 3 4 5 6 7 8 9 10 RL / R S Maximum power is transferred when RL = RS

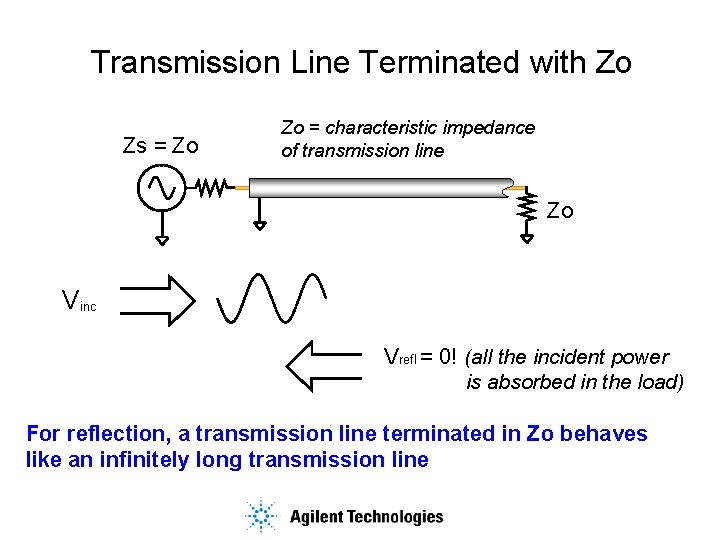
Transmission Line Terminated with Zo Zs = Zo Zo = characteristic impedance of transmission line Zo Vinc Vrefl = 0! (all the incident power is absorbed in the load) For reflection, a transmission line terminated in Zo behaves like an infinitely long transmission line

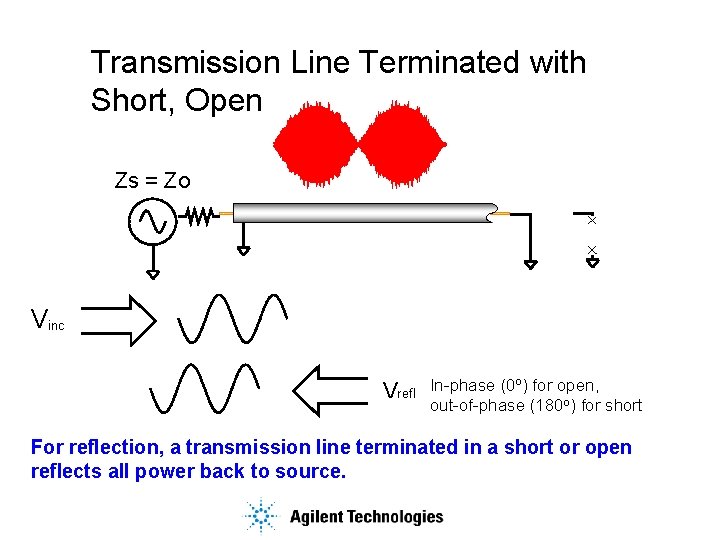
Transmission Line Terminated with Short, Open Zs = Zo Vinc Vrefl In-phase (0 o) for open, out-of-phase (180 o) for short For reflection, a transmission line terminated in a short or open reflects all power back to source.

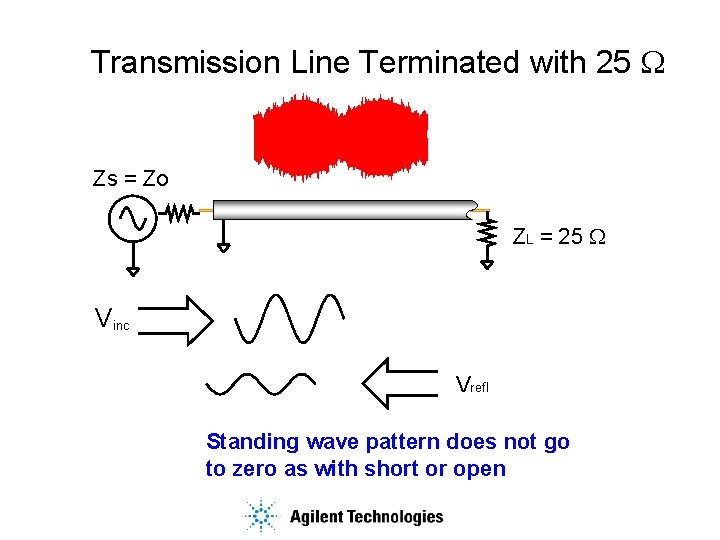
Transmission Line Terminated with 25 W Zs = Zo ZL = 25 W Vinc Vrefl Standing wave pattern does not go to zero as with short or open

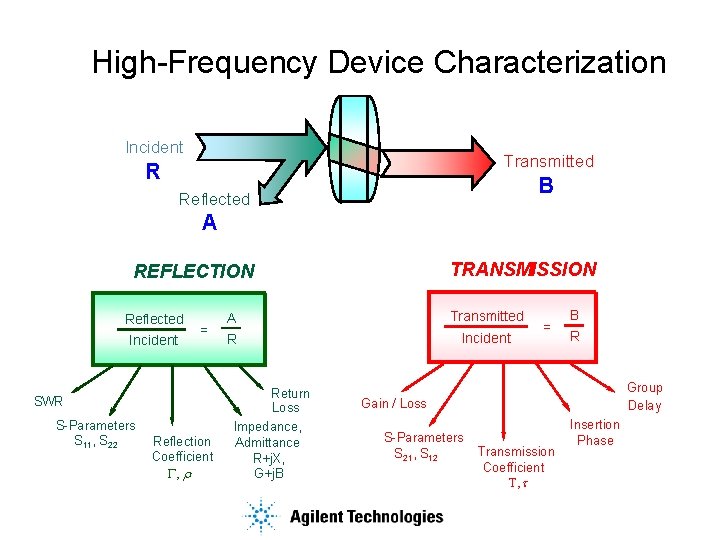
High-Frequency Device Characterization Incident Transmitted R B Reflected A TRANSMISSION REFLECTION Reflected Incident = SWR S-Parameters S 11, S 22 Reflection Coefficient G, r A Transmitted R Incident Return Loss Impedance, Admittance R+j. X, G+j. B = B R Group Delay Gain / Loss S-Parameters S 21, S 12 Transmission Coefficient T, t Insertion Phase

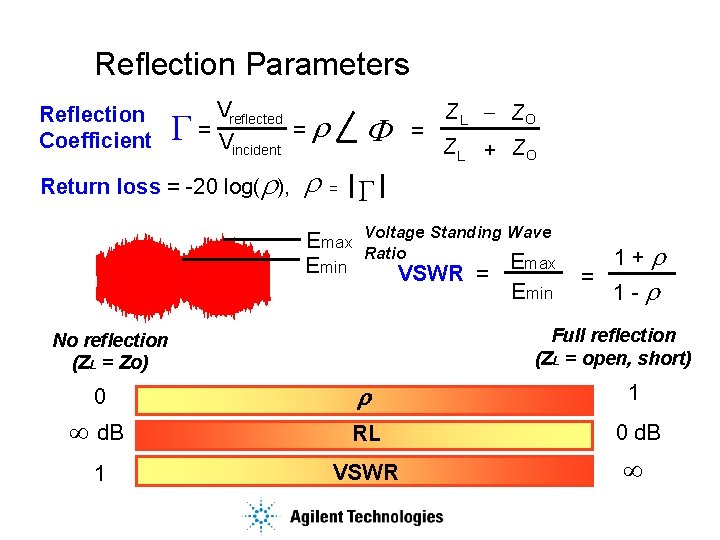
Reflection Parameters Reflection Coefficient G Vreflected = = Vincident Return loss = -20 log(r), r r F = ZL - ZO Z L + ZO G = Emax Emin Voltage Standing Wave Ratio Emax VSWR = Emin = 1+r 1 -r Full reflection (ZL = open, short) No reflection (ZL = Zo) 0 r 1 ¥ d. B RL 0 d. B 1 VSWR ¥

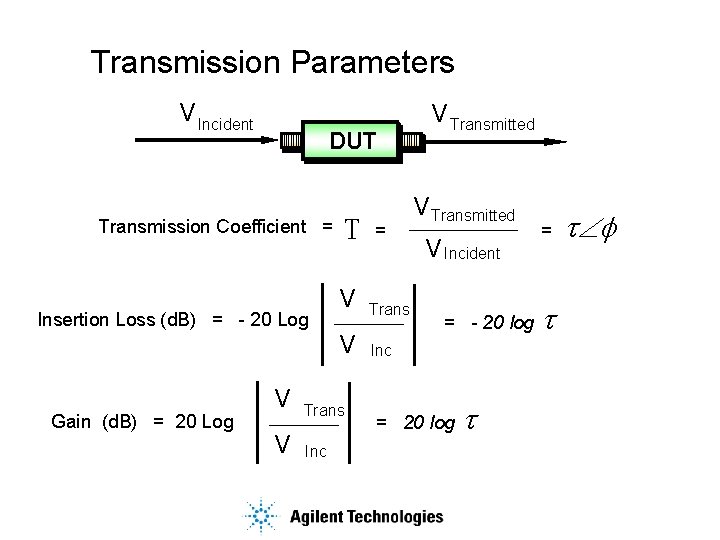
Transmission Parameters V Incident DUT Transmission Coefficient = Insertion Loss (d. B) = - 20 Log T V V Gain (d. B) = 20 Log V Trans V Inc = Trans V Transmitted V Incident = - 20 log Inc = 20 log t = t tÐf