TRAPEZUL TRAPEZUL Definiie Trapezul reprezint patrulaterul convex cu

TRAPEZUL

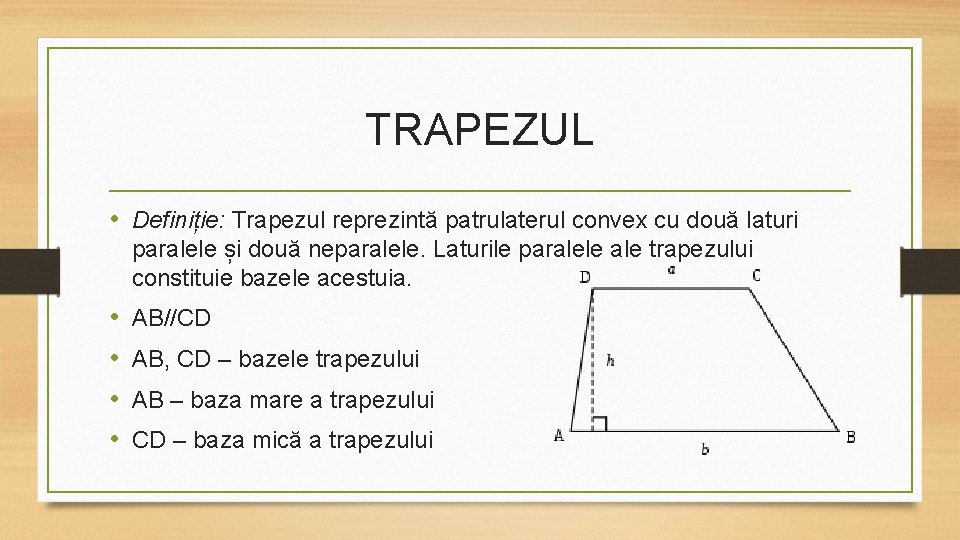
TRAPEZUL • Definiție: Trapezul reprezintă patrulaterul convex cu două laturi paralele și două neparalele. Laturile paralele ale trapezului constituie bazele acestuia. • • AB//CD AB, CD – bazele trapezului AB – baza mare a trapezului CD – baza mică a trapezului

TRAPEZUL • Definiție: Trapezul cu laturile neparalele, respectiv congruente se numește trapez isoscel. • AB//CD, AD=CB • ABCD – trapez isoscel

TRAPEZUL • TEOREME: • Teorema 1: Într-un trapez, unghiurile alăturate unei laturi neparalele sunt suplementare. • m(ABC)+m(BCD)=180}- unghiuri interne de aceeași parte a secantei • m(BAD)+m(ADC)=180}

TRAPEZUL • Teorema 2: Într-un trapez isoscel, unghiurile corespunzătoare bazei sunt respectiv congruente. • Demonstrație: Fie AN//A’B’=>NB’A’A=paralelogram=> • =>A’B’=AN, dar A’B’=AB=>AN=AB ANB= • isoscel=>m(ANB)=m(ABN)1. • m(A’B’B)=m(ANB)(unghiuri corespondente)2. • Din 1. și 2. =>m(A’B’B)=m(ABB’)=>m(B’A’A)=m(A’AB)(suplemente • de unghiuri respectiv congruente).

TRAPEZUL • Teorema 3: Trapezul cu unghiurile corespunzătoare bazei respectiv congruente se numește trapez isoscel. (Reciproca Teoremei 2. )

TRAPEZUL • Teorema 4: Într-un trapez isoscel, diagonalele sunt respectiv congruente, iar punctul lor de intersecție formează cu bazele trapezului triunghiuri isoscele. • Demonstrație: • triunghiul DAB{-DA=CB } • triunghiul CBA{- m(A)=m(B) }=>LUL=> • {AB=latură comună} =>triunghiul DAB=triunghiul CBA=>BD=AC; m(CAB)=m(ACB); m(BDC)=m(ACB), dar m(D)=m(C)=>triunghiul OAB=triunghi isoscel; m(BDC)=m(ACD)=>triunghiul ODC=triunghi isoscel

TRAPEZUL • Teorema 5: Trapezul ale cărui diagonale sunt respectiv congruente se numește trapez isoscel. (Reciproca Teoremei 4. )

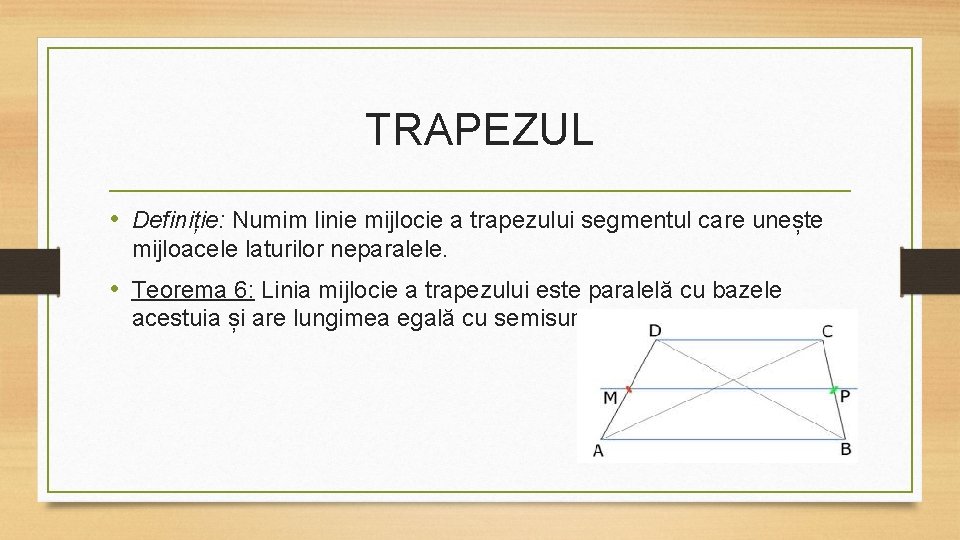
TRAPEZUL • Definiție: Numim linie mijlocie a trapezului segmentul care unește mijloacele laturilor neparalele. • Teorema 6: Linia mijlocie a trapezului este paralelă cu bazele acestuia și are lungimea egală cu semisuma bazelor.

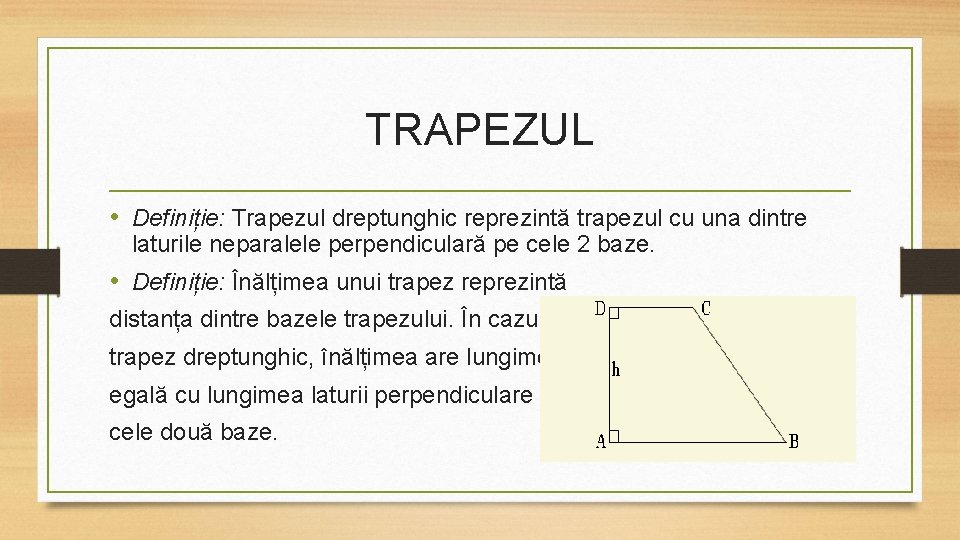
TRAPEZUL • Definiție: Trapezul dreptunghic reprezintă trapezul cu una dintre laturile neparalele perpendiculară pe cele 2 baze. • Definiție: Înălțimea unui trapez reprezintă distanța dintre bazele trapezului. În cazul unui trapez dreptunghic, înălțimea are lungimea egală cu lungimea laturii perpendiculare pe cele două baze.

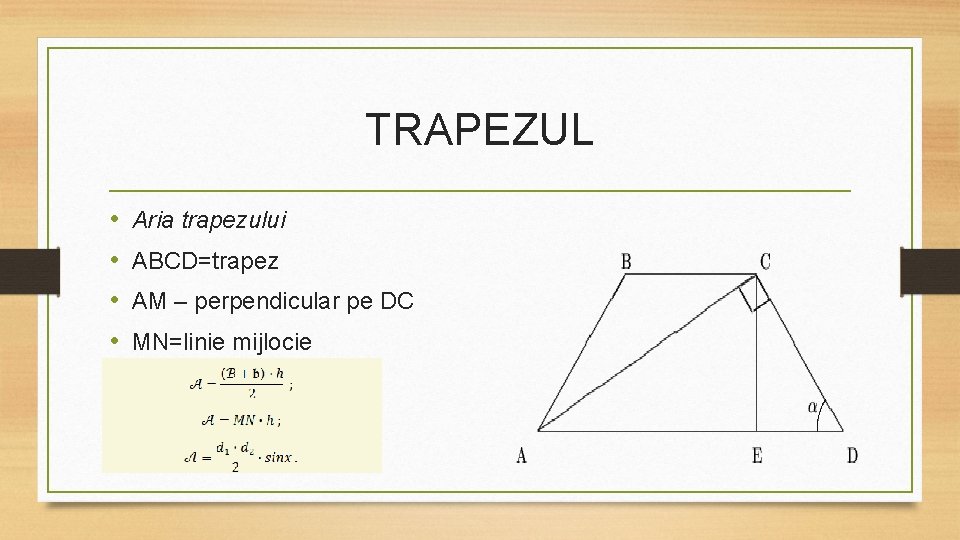
TRAPEZUL • • Aria trapezului ABCD=trapez AM – perpendicular pe DC MN=linie mijlocie

TRAPEZUL • Bibliografie: • - Google Imagini • - Culegere de matematică Paralela 45: mate 2000+ - consolidare, editura COMPER