Trapezoidal Maps Shmuel Wimer Bar Ilan Univ School

Trapezoidal Maps Shmuel Wimer Bar Ilan Univ. , School of Engineering March 2011 1

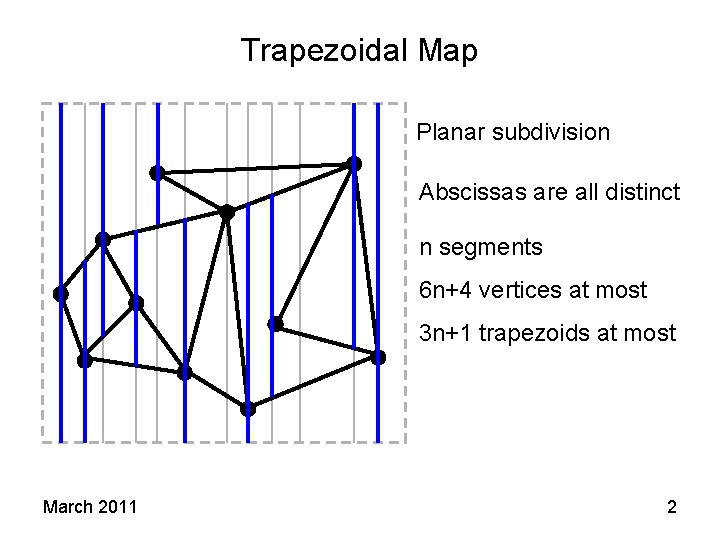
Trapezoidal Map Planar subdivision Abscissas are all distinct n segments 6 n+4 vertices at most 3 n+1 trapezoids at most March 2011 2

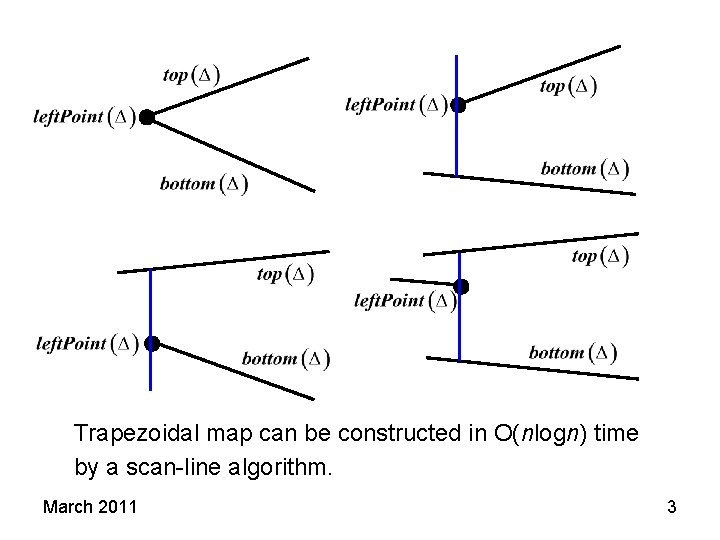
Trapezoidal map can be constructed in O(nlogn) time by a scan-line algorithm. March 2011 3

Randomized Incremental Algorithm March 2011 4

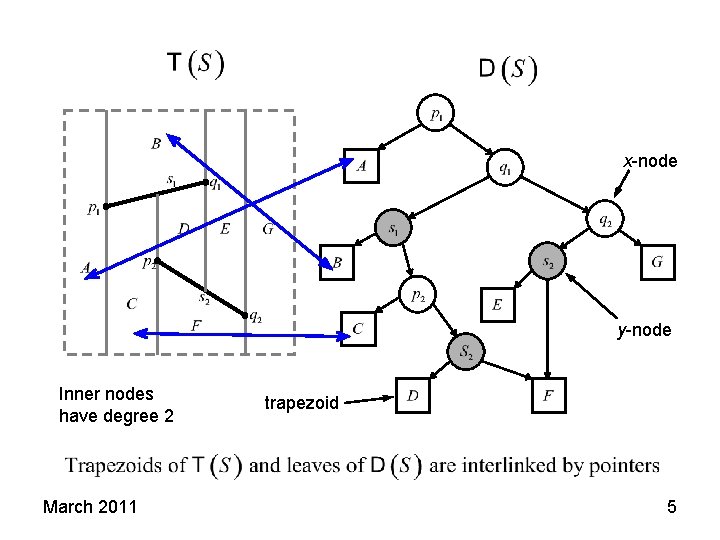
x-node y-node Inner nodes have degree 2 March 2011 trapezoid 5

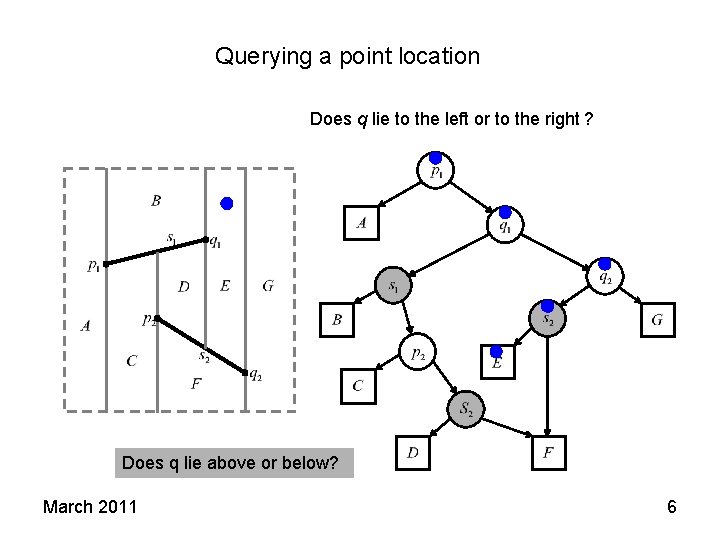
Querying a point location Does q lie to the left or to the right ? Does q lie above or below? March 2011 6

Randomized Construction Algorithm March 2011 7

March 2011 8

March 2011 9

March 2011 10

March 2011 11

March 2011 12

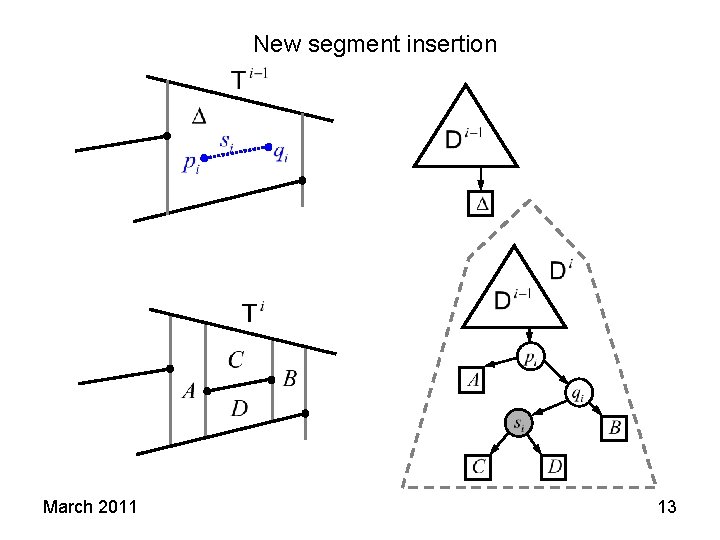
New segment insertion March 2011 13

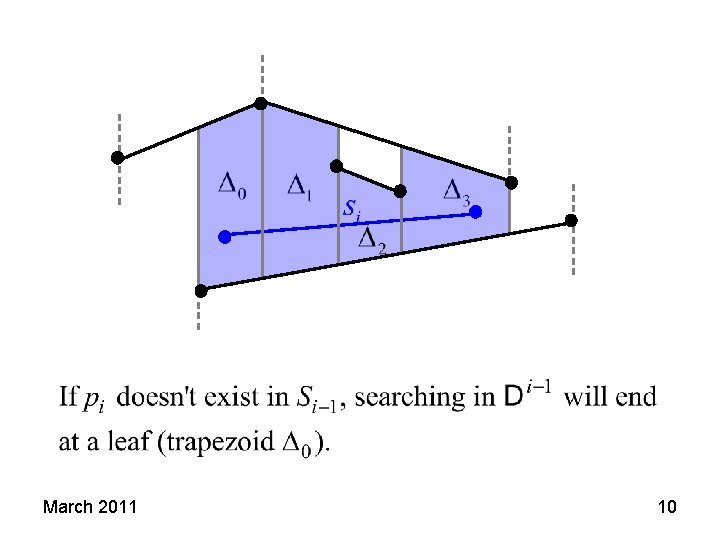
Assuming that a point is contained in Δ, the sub tree replacing its leaf is sufficient to determine whether the point is in A, B, C or D. The information attached to new trapezoids is their left and right neighbor trapezoids, top and bottom segment and points defining their left and right vertical segment. If the information in Δ is properly stored, above info can be determined in a constant time from si and Δ. If pi=left. Point(Δ) and / or qi=right. Point(Δ), Δ is divided into two or three trapezoids and sub-tree replacement is simpler. March 2011 14

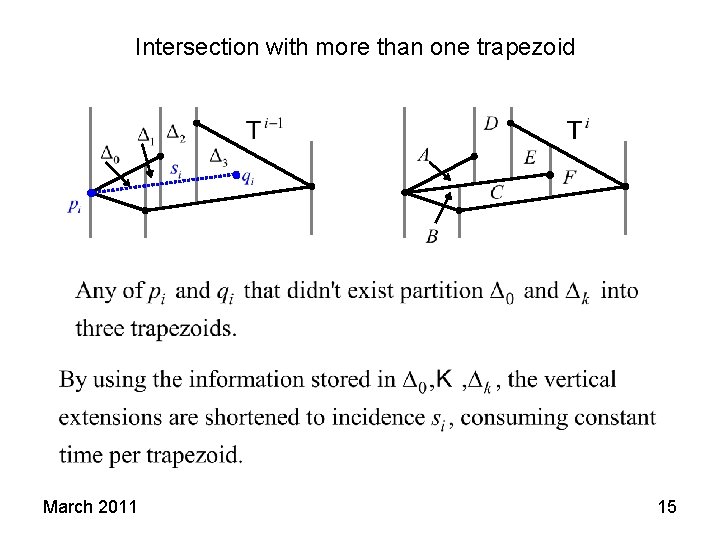
Intersection with more than one trapezoid March 2011 15

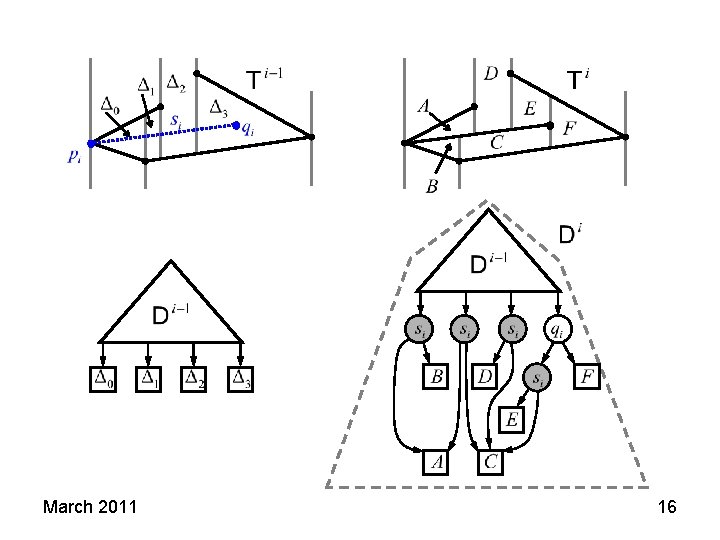
March 2011 16

March 2011 17

March 2011 18

March 2011 19

March 2011 20

March 2011 21

March 2011 22

March 2011 23

March 2011 24

■ March 2011 25

Given a set of segments, nothing is guaranteed on the maximal run time, which can be quadratic. Considering all possible problems of n segments, what is the expected maximal query time? O(logn) March 2011 26