Transverse Relaxation T 2 Relaxation For there to


- Slides: 17

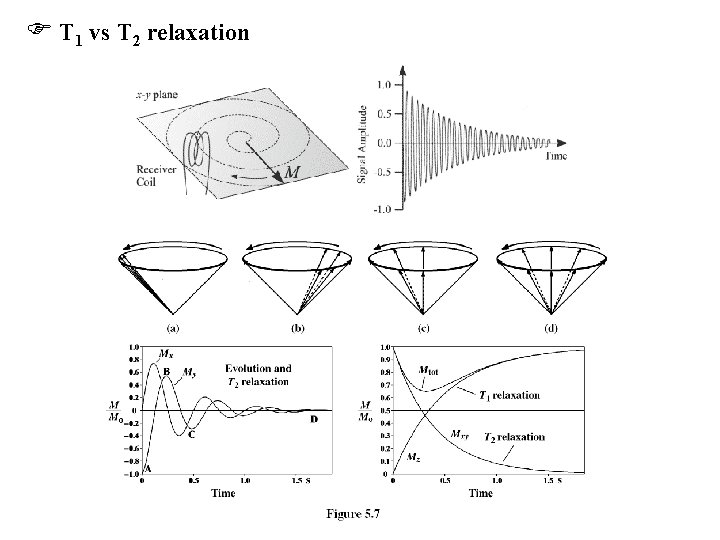
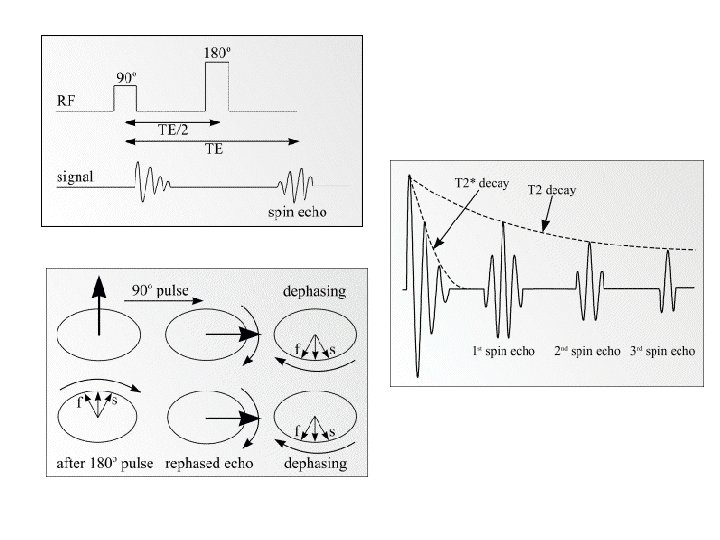
Transverse Relaxation: T 2 Relaxation For there to be net magnetization, the phases must not be random, rathere has to be a preference for one direction; this is shown in (b) in the figure above. In quantum mechanics this is described as a coherence. An RF pulse applied to equilibrium magnetization generates transverse magnetization, or in other words the pulse generates a coherence. Transverse relaxation destroys this coherence by destroying the alignment of the individual contributions.

T 1 vs T 2 relaxation

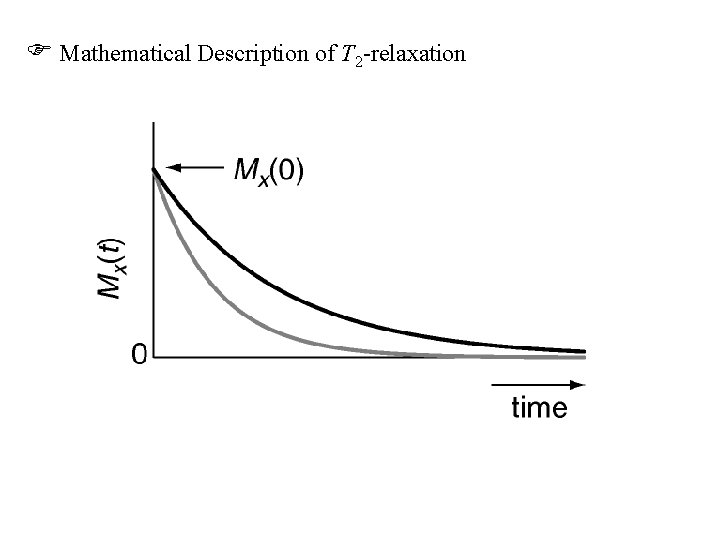
Mathematical Description of T 2 -relaxation

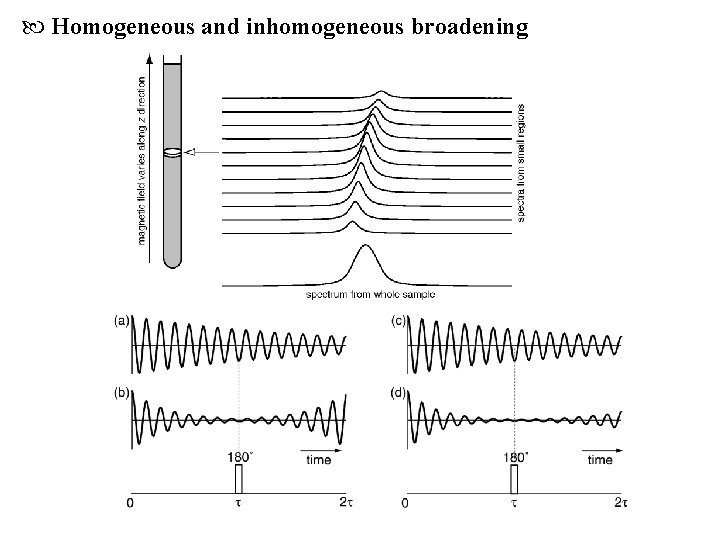
Homogeneous and inhomogeneous broadening

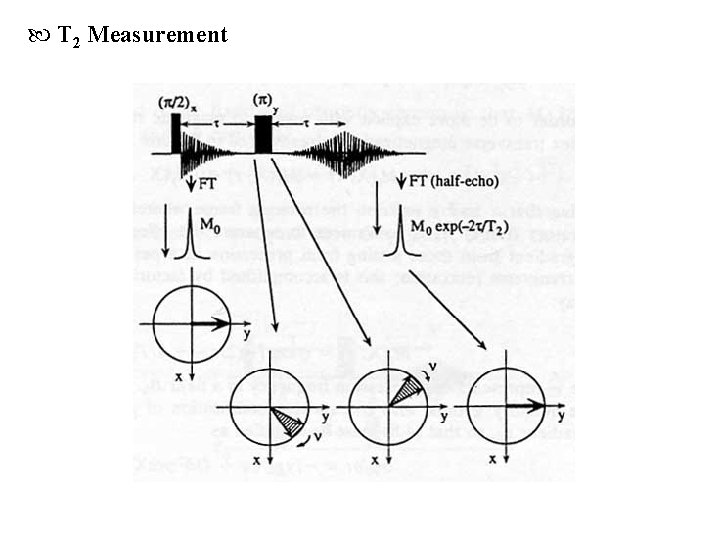
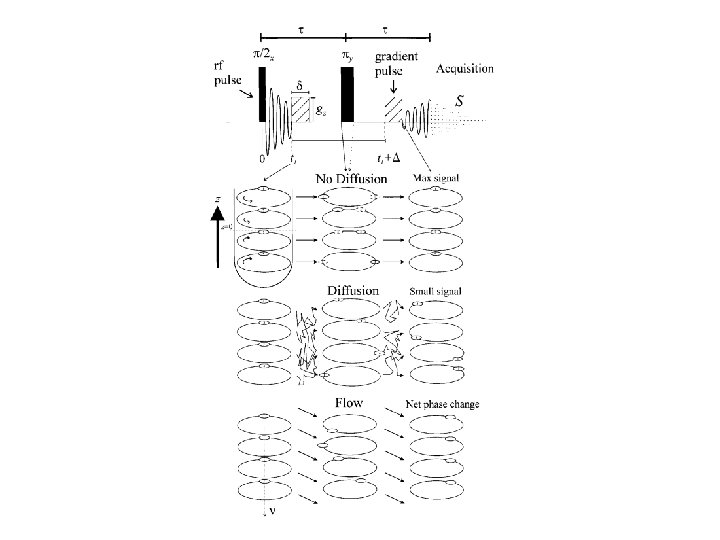
T 2 Measurement


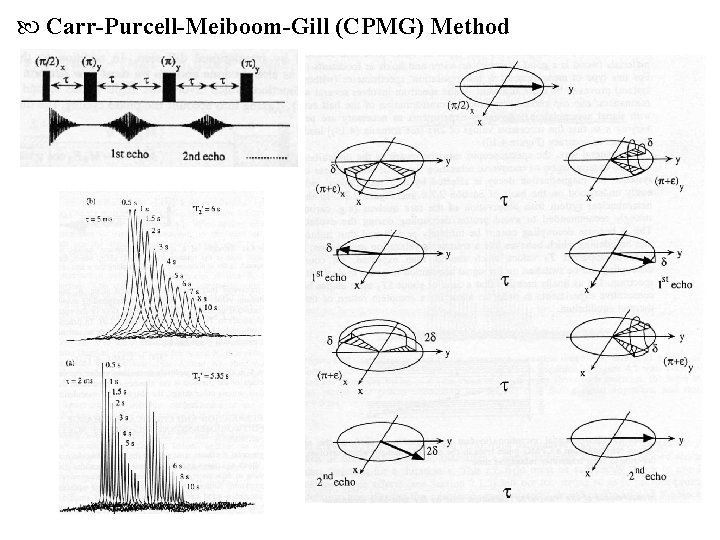
Carr-Purcell-Meiboom-Gill (CPMG) Method



Formal Treatment of the NOE Population Longitudinal Dipolar Relaxation of two spins The NOE

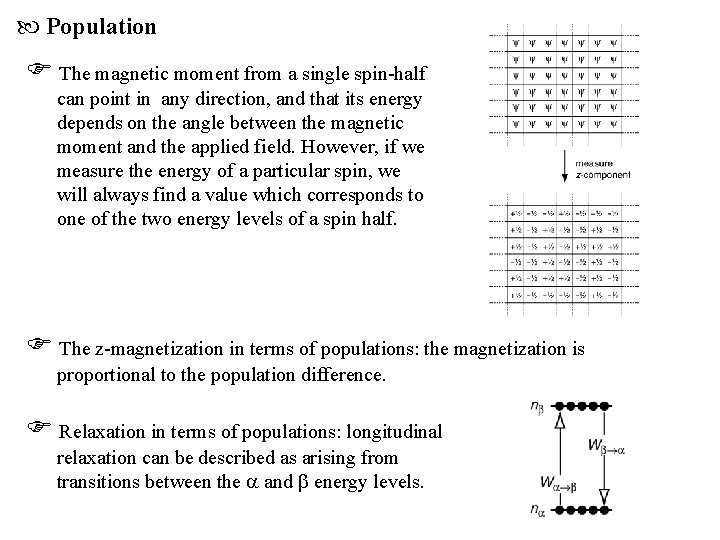
Population The magnetic moment from a single spin-half can point in any direction, and that its energy depends on the angle between the magnetic moment and the applied field. However, if we measure the energy of a particular spin, we will always find a value which corresponds to one of the two energy levels of a spin half. The z-magnetization in terms of populations: the magnetization is proportional to the population difference. Relaxation in terms of populations: longitudinal relaxation can be described as arising from transitions between the and energy levels.

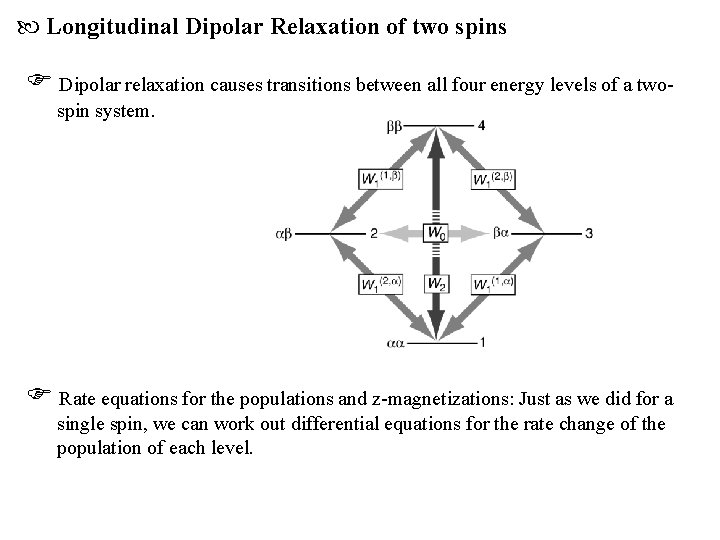
Longitudinal Dipolar Relaxation of two spins Dipolar relaxation causes transitions between all four energy levels of a twospin system. Rate equations for the populations and z-magnetizations: Just as we did for a single spin, we can work out differential equations for the rate change of the population of each level.

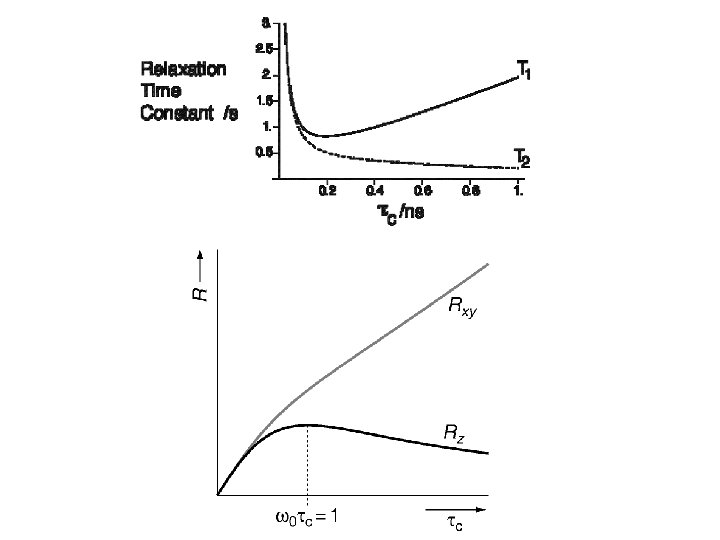
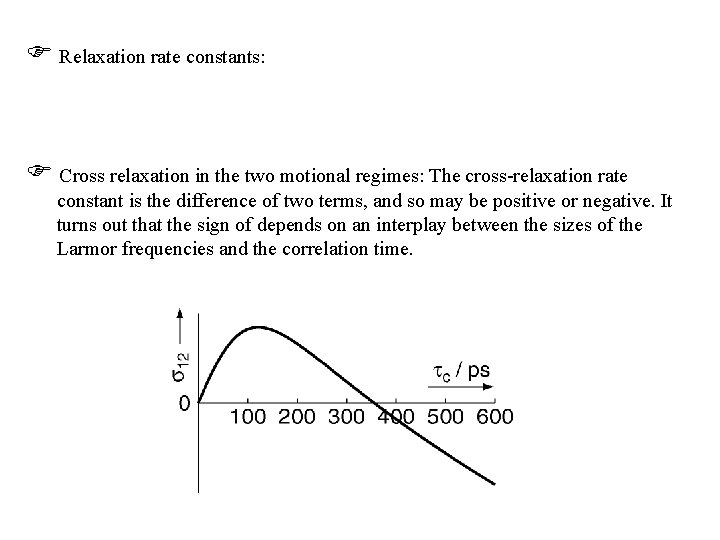
Relaxation rate constants: Cross relaxation in the two motional regimes: The cross-relaxation rate constant is the difference of two terms, and so may be positive or negative. It turns out that the sign of depends on an interplay between the sizes of the Larmor frequencies and the correlation time.

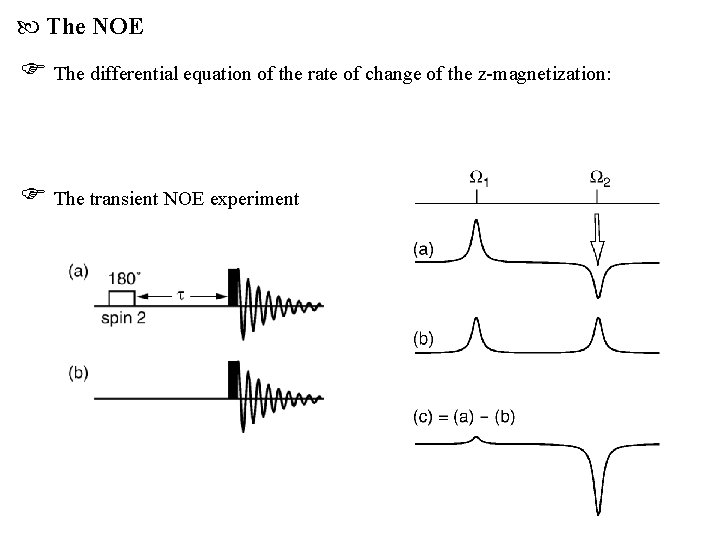
The NOE The differential equation of the rate of change of the z-magnetization: The transient NOE experiment

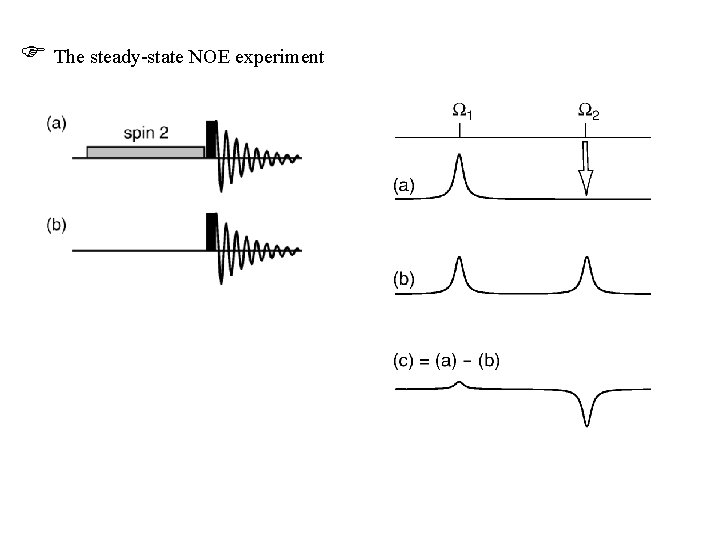
The steady-state NOE experiment

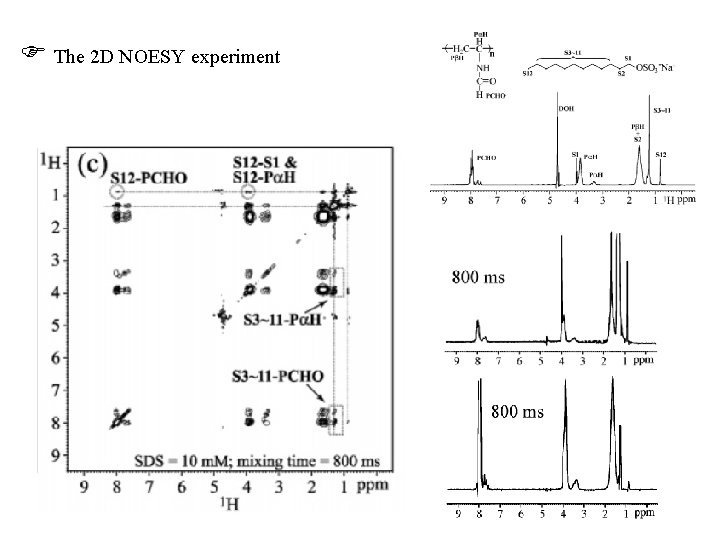
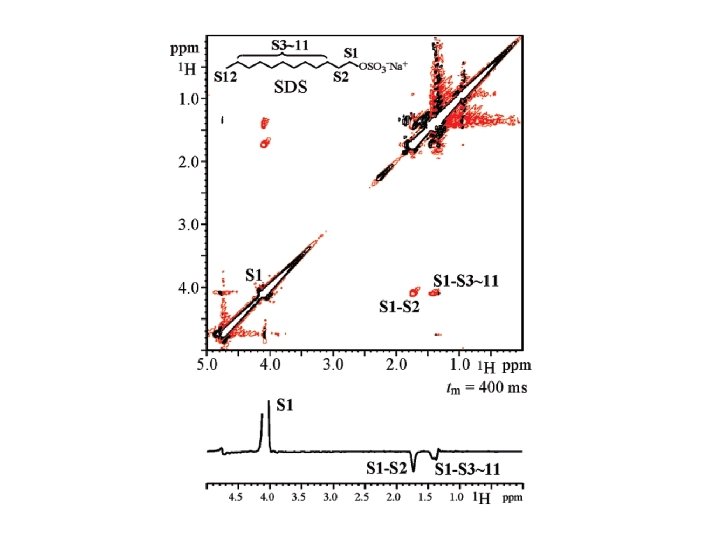
The 2 D NOESY experiment
