Transportation problem Production capacity Requirement for goods a

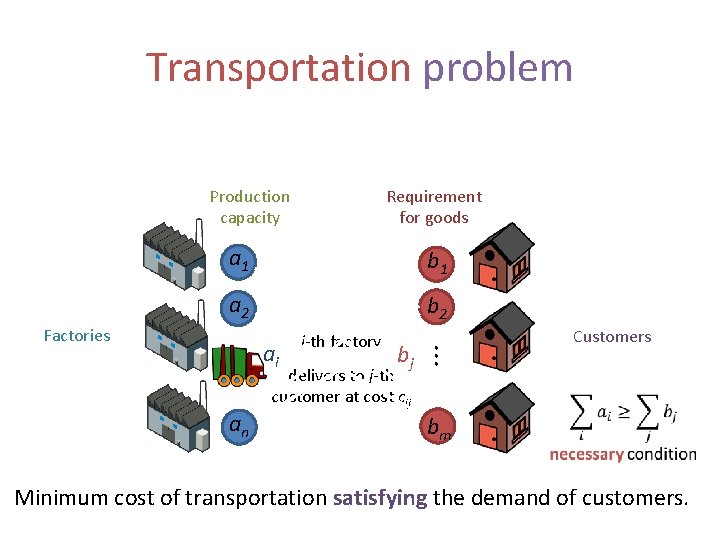
Transportation problem Production capacity Requirement for goods a 1 b 1 a 2 b 2 an ai i-th factory bj . . . Factories Customers delivers to j-th customer at cost cij bm Minimum cost of transportation satisfying the demand of customers.

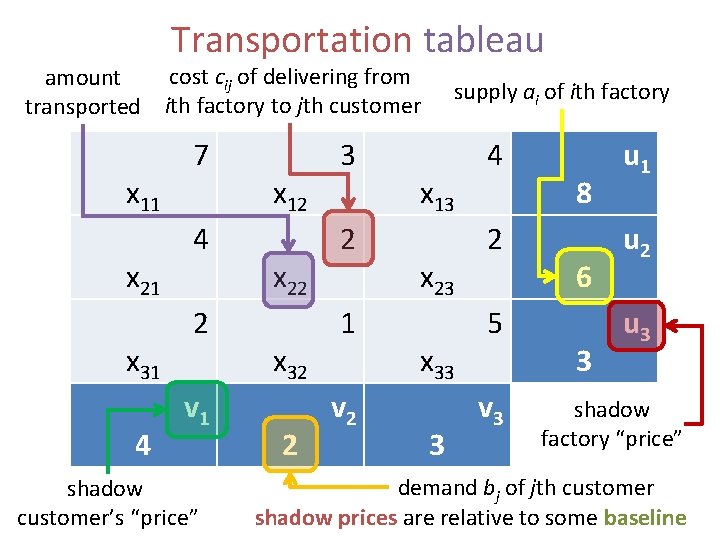
Transportation tableau cost cij of delivering from amount transported ith factory to jth customer x 11 x 21 x 31 4 7 4 2 v 1 shadow customer’s “price” x 12 x 22 x 32 2 3 2 1 v 2 supply ai of ith factory x 13 x 23 x 33 3 4 2 5 v 3 8 6 3 u 1 u 2 u 3 shadow factory “price” demand bj of jth customer shadow prices are relative to some baseline

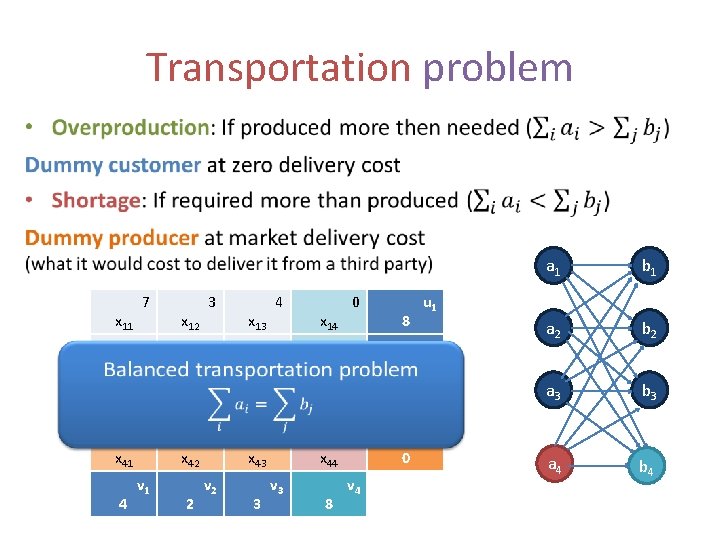
Transportation problem • x 11 x 21 x 31 x 441 4 7 4 2 v 91 v 1 x 12 x 22 x 32 x 242 2 3 2 1 v 82 v 2 x 13 x 23 x 343 3 4 2 5 v 3 11 v 3 x 814 x 624 x 334 x 844 8 u 01 u 02 u 03 v 04 v 4 8 6 3 0 a 1 b 1 a 2 b 2 a 3 b 3 a 4 b 4 u 1 u 2 u 3 u 4

Transportation Simplex • Applying the Simplex method to the problem • Basic solution – min-cost method • Pivoting – shadow prices set u 1 = 0, then ui + vj=cij – reduced cost pivot if ui + vj > cij • Finding a loop cost = 3× 7 + 3× 4 + 2× 0 + 1× 2 + 2× 1 + 6× 0 = 37 x 311 x 21 x 131 34 0 7 4 2 v 1 x 12 x 232 02 3 2 1 v 2 x 313 x 23 x 33 30 4 2 5 v 3 x 214 x 624 x 34 0 82 0 0 0 v 4 680 06 130 u 1 u 2 u 3 z = 37 must mark takeexactly the smaller m + nof – the 1 = 6 two cells

Transportation Simplex • Applying the Simplex method to the problem • Basic solution – min-cost method • Pivoting – shadow prices set u 1 = 0, then ui + vj=cij – reduced cost pivot if ui + vj > cij • Finding a loop x 311 x 21 x 131 4 7 4 2 v 71 x 12 x 232 2 3 2 1 v 62 x 313 x 23 x 33 3 4 2 5 x 214 x 624 x 34 v 43 ui =0 and vj must sum up to cij = 4 8 0 0 0 v 04 8 6 3 u 01 u 02 -5 u 3 z = 37 vj = 4

Transportation Simplex • Applying the Simplex method to the problem • Basic solution – min-cost method • Pivoting – shadow prices set u 1 = 0, then ui + vj=cij – reduced cost pivot if ui + vj > cij • Finding a loop 7 6 >3 x 311 x 12 x 313 4 7>4 6>2 4>2 x 21 x 22 x 23 x 131 4 2 v 71 x 214 x 624 0 0 1 -1 ≤ 5 -5 ≤ 0 x 232 x 33 x 34 2 v 62 3 v 43 calculate ui + vj 8 v 04 8 6 3 u 01 u 02 -5 u 3 z = 37

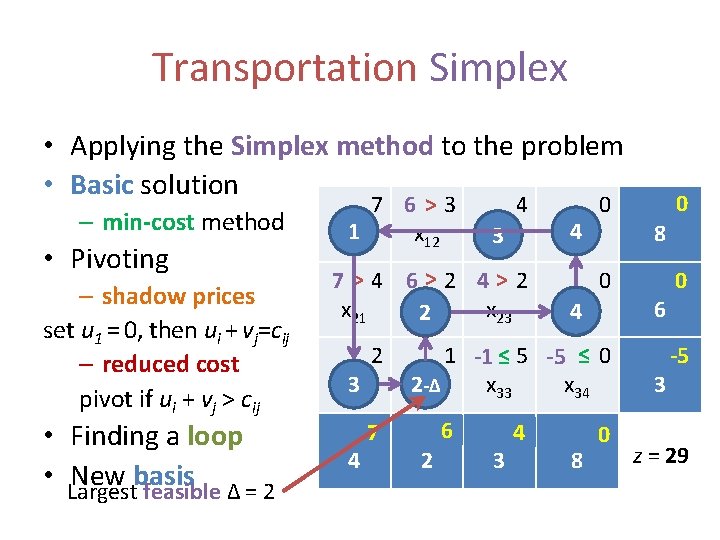
Transportation Simplex • Applying the Simplex method to the problem • Basic solution – min-cost method • Pivoting – shadow prices set u 1 = 0, then ui + vj=cij – reduced cost pivot if ui + vj > cij • Finding a loop • Largest New basis feasible Δ = 2 7 6 >3 3 x 13 -Δ x 12 11 x 313 4 7>4 6>2 4>2 x 21 x 222 x 23 +Δ 1 x 31+Δ 31 4 2 v 71 2+Δ 2 x 4 14 6 x 4 6 -Δ 24 0 0 1 -1 ≤ 5 -5 ≤ 0 2 x 2 -Δ x 33 x 34 32 2 v 62 3 v 43 8 v 04 8 6 3 u 01 u 02 -5 u 3 z = 37 29