Transportation Assignment and Transshipment Professor Ahmadi Slide 1

Transportation, Assignment, and Transshipment Professor Ahmadi Slide 1

Chapter 7 Transportation, Assignment, and Transshipment Problems n n n The Transportation Problem: The Network Model and a Linear Programming Formulation The Assignment Problem: The Network Model and a Linear Programming Formulation The Transshipment Problem: The Network Model and a Linear Programming Formulation Slide 2

Transportation, Assignment, and Transshipment Problems n n A network model is one which can be represented by a set of nodes, a set of arcs, and functions (e. g. costs, supplies, demands, etc. ) associated with the arcs and/or nodes. Transportation, assignment, and transshipment problems are all examples of network problems. Slide 3

Transportation, Assignment, and Transshipment Problems n n n Each of the three models of this chapter (transportation, assignment, and transshipment models) can be formulated as linear programs. For each of the three models, if the right-hand side of the linear programming formulations are all integers, the optimal solution will be in terms of integer values for the decision variables. These three models can also be solved using a standard computer spreadsheet package. Slide 4

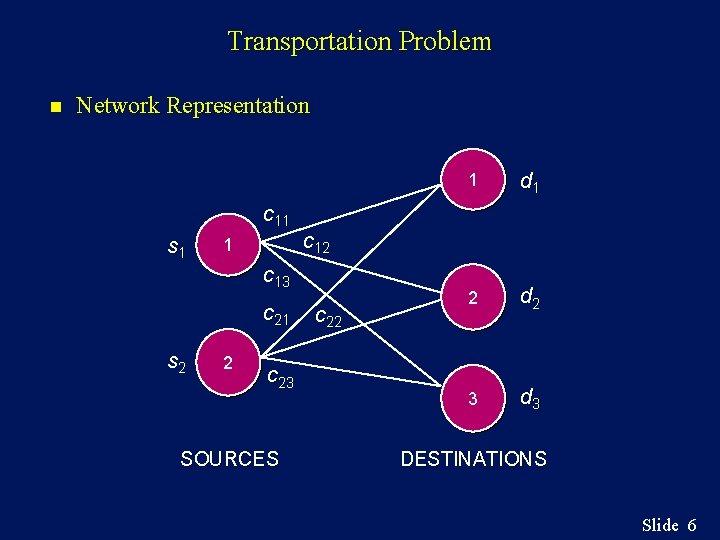
Transportation Problem n n The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply si) to n destinations (each with a demand dj), when the unit shipping cost from an origin, i, to a destination, j, is cij. The network representation for a transportation problem with two sources and three destinations is given on the next slide. Slide 5

Transportation Problem n Network Representation c 11 s 1 1 s 2 2 c 23 SOURCES d 1 2 d 2 3 d 3 c 12 c 13 c 21 1 c 22 DESTINATIONS Slide 6

Transportation Problem n LP Formulation The linear programming formulation in terms of the amounts shipped from the origins to the destinations, xij, can be written as: Min SScijxij ij s. t. Sxij < si for each origin i j Sxij = dj for each destination j i xij > 0 for all i and j Slide 7

Transportation Problem n LP Formulation Special Cases The following special-case modifications to the linear programming formulation can be made: • Minimum shipping guarantees from i to j: xij > Lij • Maximum route capacity from i to j: xij < Lij • Unacceptable routes: delete the variable Slide 8

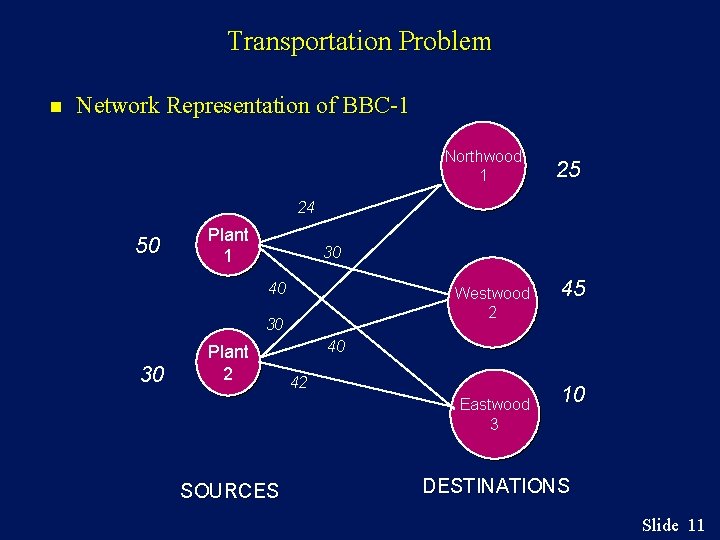
Example: BBC-1 Building Brick Company (BBC) has orders for 80 tons of bricks at three suburban locations as follows: Northwood -25 tons, Westwood -- 45 tons, and Eastwood -- 10 tons. BBC has two plants. Plant 1 produces 50 and plant 2 produces 30 tons per week. How should end of week shipments be made to fill the above orders given the following delivery cost per ton: Northwood Westwood Eastwood Plant 1 24 30 40 Plant 2 30 40 42 Slide 9

Example: BBC-1 n LP Formulation • Decision Variables Defined xij = amount shipped from plant i to suburb j where i = 1 (Plant 1) and 2 (Plant 2) j = 1 (Northwood), 2 (Westwood), and 3 (Eastwood) Slide 10

Transportation Problem n Network Representation of BBC-1 Northwood 1 25 24 50 Plant 1 30 40 Westwood 2 30 30 Plant 2 40 42 Eastwood 3 SOURCES 45 10 DESTINATIONS Slide 11

Example: BBC-1 n LP Formulation • Objective Function Minimize total shipping cost per week: Min 24 x 11 + 30 x 12 + 40 x 13 + 30 x 21 + 40 x 22 + 42 x 23 • Constraints s. t. x 11 + x 12 + x 13 < 50 (Plant 1 capacity) x 21 + x 22 + x 23 < 30 (Plant 2 capacity) x 11 + x 21 = 25 (Northwood demand) x 12 + x 22 = 45 (Westwood demand) x 13 + x 23 = 10 (Eastwood demand) all xij > 0 (Non-negativity) Slide 12

Example: BBC-1 n Optimal Solution From Plant 1 Plant 2 To Amount Cost Northwood 5 120 Westwood 45 1, 350 Northwood 20 600 Eastwood 10 420 Total Cost = $2, 490 Slide 13

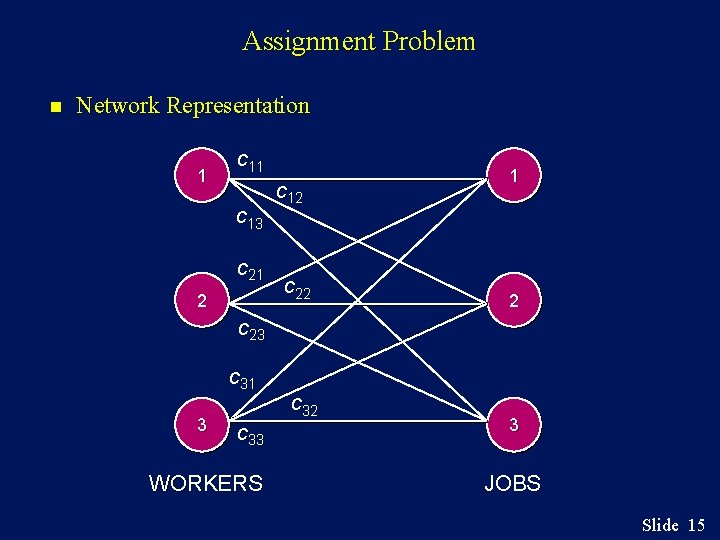
Assignment Problem n n An assignment problem seeks to minimize the total cost assignment of m workers to m jobs, given that the cost of worker i performing job j is cij. It assumes all workers are assigned and each job is performed. An assignment problem is a special case of a transportation problem in which all supplies and all demands are equal to 1; hence assignment problems may be solved as linear programs. The network representation of an assignment problem with three workers and three jobs is shown on the next slide. Slide 14

Assignment Problem n Network Representation 1 c 13 c 21 2 c 12 c 22 1 2 c 23 c 31 3 c 33 WORKERS c 32 3 JOBS Slide 15

Assignment Problem n Linear Programming Formulation Min SScijxij ij s. t. Sxij = 1 j Sxij = 1 i xij = 0 or 1 for each worker i for each job j for all i and j. • Note: A modification to the right-hand side of the first constraint set can be made if a worker is permitted to work more than one job. Slide 16

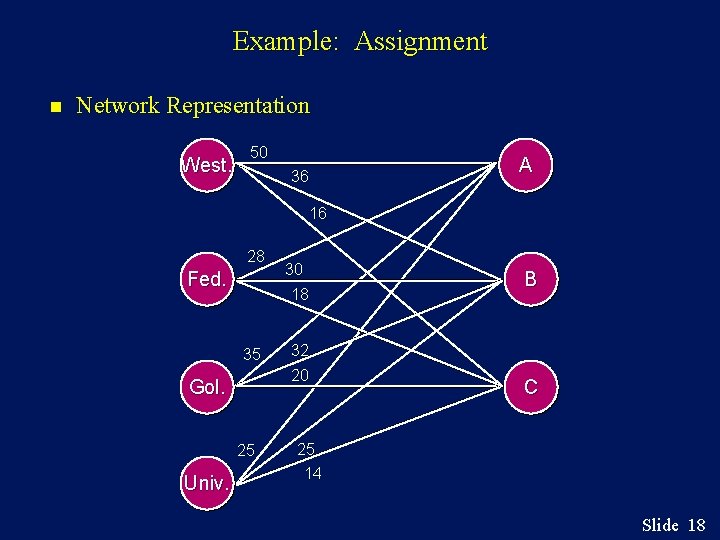
Example: Assignment A contractor pays his subcontractors a fixed fee plus mileage for work performed. On a given day the contractor is faced with three electrical jobs associated with various projects. Given below are the distances between the subcontractors and the projects. Project A B C Westside 50 36 16 Subcontractors Federated 28 30 18 Goliath 35 32 20 Universal 25 25 14 How should the contractors be assigned to minimize total distance (and total cost)? Slide 17

Example: Assignment n Network Representation West. 50 36 A 16 28 Fed. 35 Gol. 25 Univ. 30 18 32 20 B C 25 14 Slide 18

Example: Assignment n LP Formulation • Decision Variables Defined xij = 1 if subcontractor i is assigned to project j = 0 otherwise where: i = 1 (Westside), 2 (Federated), 3 (Goliath), and 4 (Universal) j = 1 (A), 2 (B), and 3 (C) Slide 19

Example: Assignment n LP Formulation • Objective Function Minimize total distance: Min 50 x 11 + 36 x 12 + 16 x 13 + 28 x 21 + 30 x 22 + 18 x 23 + 35 x 31 + 32 x 32 + 20 x 33 + 25 x 41 + 25 x 42 + 14 x 43 Slide 20

Example: Assignment n LP Formulation • Constraints x 11 + x 12 + x 13 < 1 (no more than one x 21 + x 22 + x 23 < 1 project assigned x 31 + x 32 + x 33 < 1 to any one x 41 + x 42 + x 43 < 1 subcontractor) x 11 + x 21 + x 31 + x 41 = 1 (each project must x 12 + x 22 + x 32 + x 42 = 1 be assigned to just x 13 + x 23 + x 33 + x 43 = 1 one subcontractor) all xij > 0 (non-negativity) Slide 21

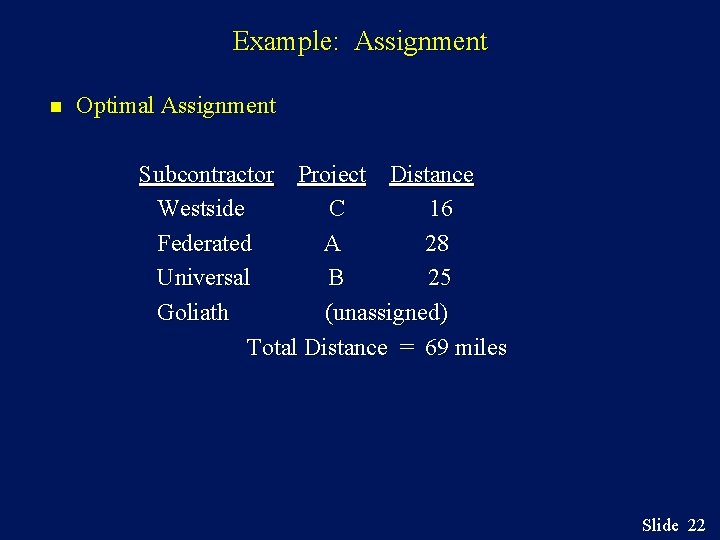
Example: Assignment n Optimal Assignment Subcontractor Project Distance Westside C 16 Federated A 28 Universal B 25 Goliath (unassigned) Total Distance = 69 miles Slide 22

Variations of Assignment Problem n n n Total number of agents not equal to total number of tasks Maximization objective function Unacceptable assignments Slide 23

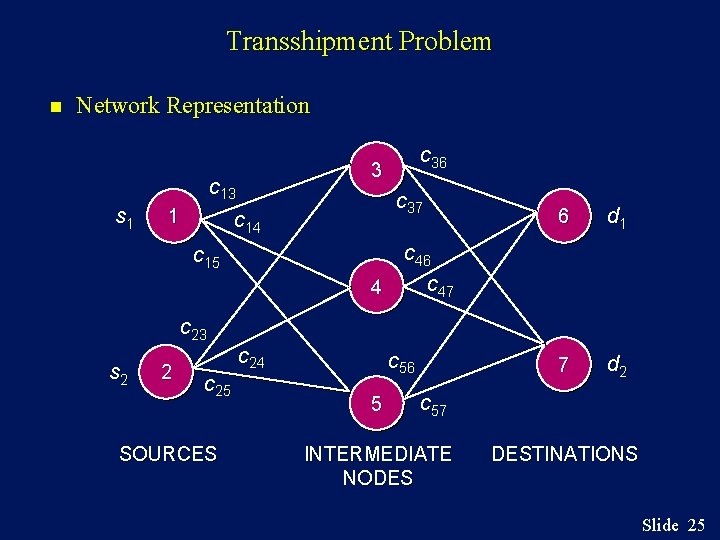
Transshipment Problem n n Transshipment problems are transportation problems in which a shipment may move through intermediate nodes (transshipment nodes)before reaching a particular destination node. Transshipment problems can be converted to larger transportation problems and solved by a special transportation program. Transshipment problems can also be solved as linear programs. The network representation for a transshipment problem with two sources, three intermediate nodes, and two destinations is shown on the next slide. Slide 24

Transshipment Problem n Network Representation s 1 c 13 c 14 1 s 2 2 c 25 SOURCES 3 c 37 6 d 1 7 d 2 c 46 c 47 4 c 15 c 23 c 36 c 24 c 56 5 c 57 INTERMEDIATE NODES DESTINATIONS Slide 25

Transshipment Problem n Linear Programming Formulation xij represents the shipment from node i to node j Min S cijxij all arcs s. t. S xij - S xij < si for each origin node i S xij - S xij = 0 for each intermediate node arcs out arcs in S xij - S xij = -dj for each destination node j (Note the order) arcs in xij > 0 for all i and j Slide 26

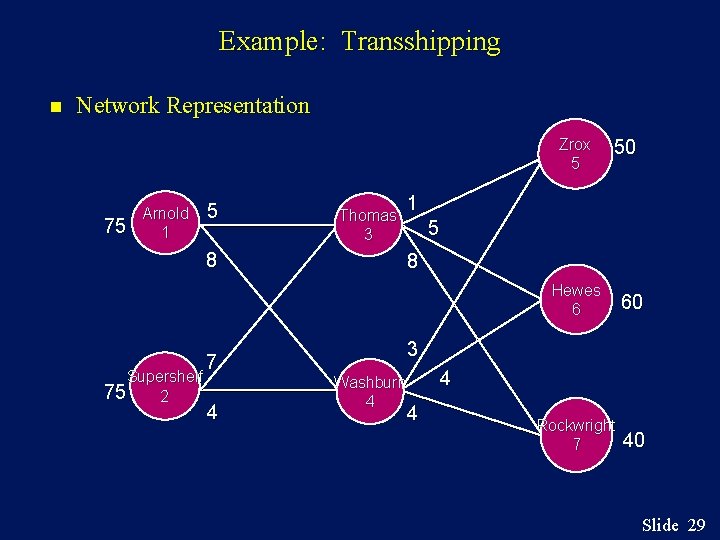
Example: Transshipping Thomas Industries and Washburn Corporation supply three firms (Zrox, Hewes, Rockwright) with customized shelving for its offices. They both order shelving from the same two manufacturers, Arnold Manufacturers and Supershelf, Inc. Currently weekly demands by the users are 50 for Zrox, 60 for Hewes, and 40 for Rockwright. Both Arnold and Supershelf can supply at most 75 units to its customers. Additional data is shown on the next slide. Slide 27

Example: Transshipping Because of long standing contracts based on past orders, unit costs from the manufacturers to the suppliers are: Thomas Washburn Arnold 5 8 Supershelf 7 4 The cost to install the shelving at the various locations are: Zrox Hewes Rockwright Thomas 1 5 8 Washburn 3 4 4 Slide 28

Example: Transshipping n Network Representation ZROX Zrox 5 75 Arnold ARNOLD 1 5 8 Supershelf 75 2 7 4 50 1 Thomas 3 5 8 Hewes HEWES 6 60 Rockwright 7 40 3 Washburn WASH BURN 4 4 4 Slide 29

Example: Transshipping n LP Formulation • Decision Variables Defined xij = amount shipped from manufacturer i to supplier j xjk = amount shipped from supplier j to customer k where i = 1 (Arnold), 2 (Supershelf) j = 3 (Thomas), 4 (Washburn) k = 5 (Zrox), 6 (Hewes), 7 (Rockwright) • Objective Function Defined Minimize Overall Shipping Costs: Min 5 x 13 + 8 x 14 + 7 x 23 + 4 x 24 + 1 x 35 + 5 x 36 + 8 x 37 + 3 x 45 + 4 x 46 + 4 x 47 Slide 30

Example: Transshipping n Constraints Defined Amount out of Arnold: Amount out of Supershelf: Amount through Thomas: Amount through Washburn: Amount into Zrox: Amount into Hewes: Amount into Rockwright: x 13 + x 14 < 75 x 23 + x 24 < 75 x 13 + x 23 - x 35 - x 36 - x 37 = 0 x 14 + x 24 - x 45 - x 46 - x 47 = 0 x 35 + x 45 = 50 x 36 + x 46 = 60 x 37 + x 47 = 40 Non-negativity of variables: xij > 0, for all i and j. Slide 31

Variations of Transshipment Problem n n Total supply not equal to total demand Maximization objective function Route capacities or route minimums Unacceptable routes Slide 32

The End of Chapter Slide 33