Transport through junctions of interacting quantum wires and































- Slides: 40

Transport through junctions of interacting quantum wires and nanotubes R. Egger Institut für Theoretische Physik Heinrich-Heine Universität Düsseldorf S. Chen, S. Gogolin, H. Grabert, A. Komnik, H. Saleur, F. Siano, B. Trauzettel

Overview n n n Introduction: Luttinger liquid in nanotubes Multi-terminal circuits Landauer-Büttiker theory for junction of interacting quantum wires Local Coulomb drag: Conductance and perfect shot noise locking Multi-wall nanotubes Conclusions and outlook

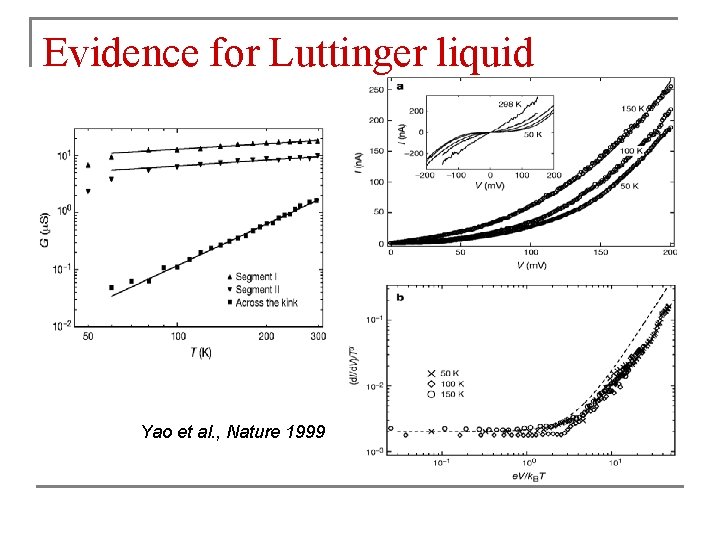
Single-wall carbon nanotubes n Prediction: SWNT is a Luttinger liquid with g~0. 2 to 0. 3 Egger & Gogolin, PRL 1997 Kane, Balents & Fisher, PRL 1997 n Experiment: Luttinger power-law conductance through weak link, gives g~0. 22 Yao et al. , Nature 1999 Bockrath et al. , Nature 1999

Conductance scaling n Conductance across kink: n Universal scaling of nonlinear conductance: r. h. s. is only function of V/T

Evidence for Luttinger liquid Yao et al. , Nature 1999

Luttinger liquid properties n n n Momentum distribution: no jump at Fermi surface, power-law scaling Tunneling density of states power-law suppressed, with different end/bulk exponent Spin-charge separation Fractional charge and statistics Networks of nanotubes: Experiment? Theory? Dekker group, Delft

Multi-terminal circuits: Crossed tubes By chance… Fuhrer et al. , Science 2000 Fusion: Electron beam welding (transmission electron microscope) Terrones et al. , PRL 2002

Nanotube Y junctions Li et al. , Nature 1999

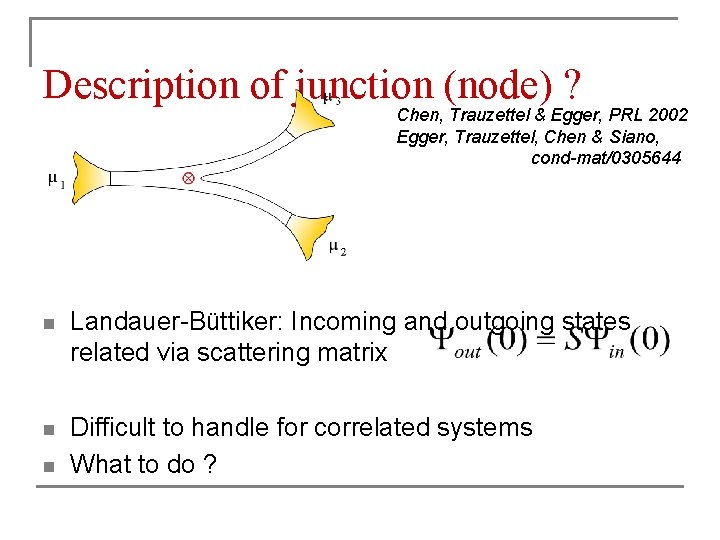
Landauer-Büttiker theory ? n Standard scattering approach useless: q q n Elementary excitations are fractionalized quasiparticles, not electrons No simple scattering of electrons, neither at junction nor at contact to reservoirs Generalization to Luttinger liquids q q Coupling to reservoirs via radiative boundary conditions Junction: Boundary condition plus impurities

Coupling to voltage reservoirs n Two-terminal case, applied voltage n Left/right reservoir injects `bare´ density of R/L moving charges n Screening: actual charge density is Egger & Grabert, PRL 1997

Radiative boundary conditions Egger & Grabert, PRB 1998 Safi, EPJB 1999 n n Difference of R/L currents unaffected by screening: Solve for injected densities boundary conditions for chiral density near adiabatic contacts

Radiative boundary conditions … n n hold for arbitrary correlations and disorder in Luttinger liquid imposed in stationary state apply to multi-terminal geometries preserve integrability, full two-terminal transport problem solvable by thermodynamic Bethe ansatz Egger, Grabert, Koutouza, Saleur & Siano, PRL 2000

Description of junction (node) ? Chen, Trauzettel & Egger, PRL 2002 Egger, Trauzettel, Chen & Siano, cond-mat/0305644 n Landauer-Büttiker: Incoming and outgoing states related via scattering matrix n Difficult to handle for correlated systems What to do ? n

Some recent proposals … n Perturbation theory in interactions Lal, Rao & Sen, PRB 2002 n n Perturbation theory for almost no transmission Safi, Devillard & Martin, PRL 2001 Node as island Nayak, Fisher, Ludwig & Lin, PRB 1999 Node as ring Chamon, Oshikawa & Affleck, cond-mat/0305121 Our approach: Node boundary condition for ideal symmetric junction (exactly solvable) q additional impurities generate arbitrary S matrices, no conceptual problem Chen, Trauzettel & Egger, PRL 2002

Ideal symmetric junctions n N>2 branches, junction with S matrix Crossover from full to no transmission tuned by λ n implies wavefunction matching at node

Boundary conditions at the node n n Wavefunction matching implies density matching can be handled for Luttinger liquid Additional constraints: q q n Kirchhoff node rule Gauge invariance Nonlinear conductance matrix can then be computed exactly for arbitrary parameters

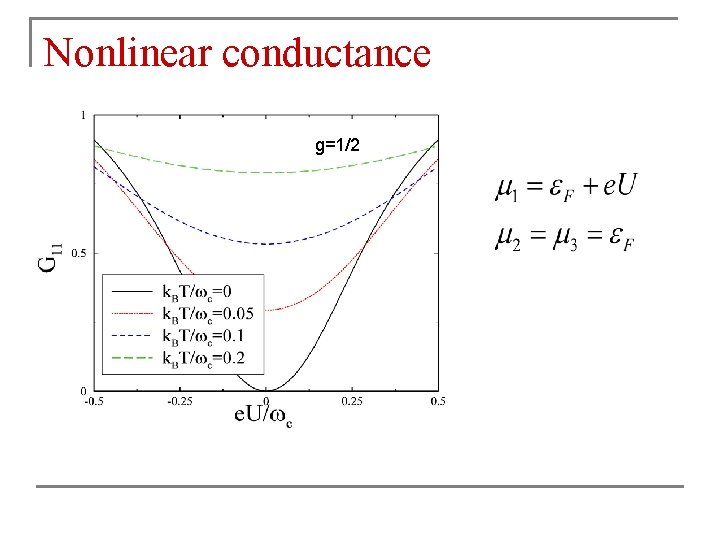
Solution for Y junction with g=1/2 Nonlinear conductance: with

Nonlinear conductance g=1/2

Ideal junction: Fixed point n n Symmetric system breaks up into disconnected wires at low energies Only stable fixed point Typical Luttinger power law for all conductance coefficients Solvable for arbitrary correlations g=1/3

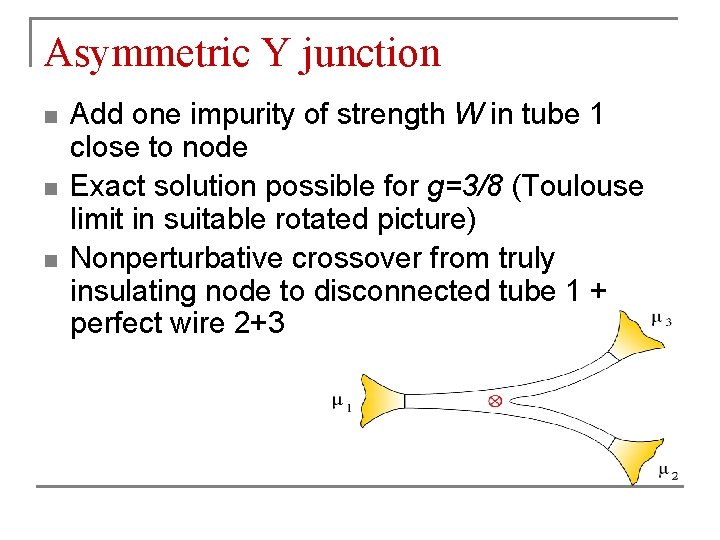
Asymmetric Y junction n Add one impurity of strength W in tube 1 close to node Exact solution possible for g=3/8 (Toulouse limit in suitable rotated picture) Nonperturbative crossover from truly insulating node to disconnected tube 1 + perfect wire 2+3

Asymmetric Y junction: g=3/8 n Nonperturbative solution: n Asymmetry contribution n Strong asymmetry limit:

Crossed tubes: Local Coulomb drag Komnik & Egger, PRL 1998, EPJB 2001 n Different limit: Weakly coupled crossed nanotubes q q n Single-electron tunneling between tubes irrelevant Electrostatic coupling relevant for strong interactions, Without tunneling: Local Coulomb drag

Hamiltonian for crossed tubes n Without tunneling: n Rotated boson fields: n Boundary condition decouples: Hamiltonian also decouples! n

Map to decoupled 2 -terminal models n Two effective two-terminal (single impurity) problems for n Take over exact solution for two-terminal problem Dependence of current on cross voltage? n

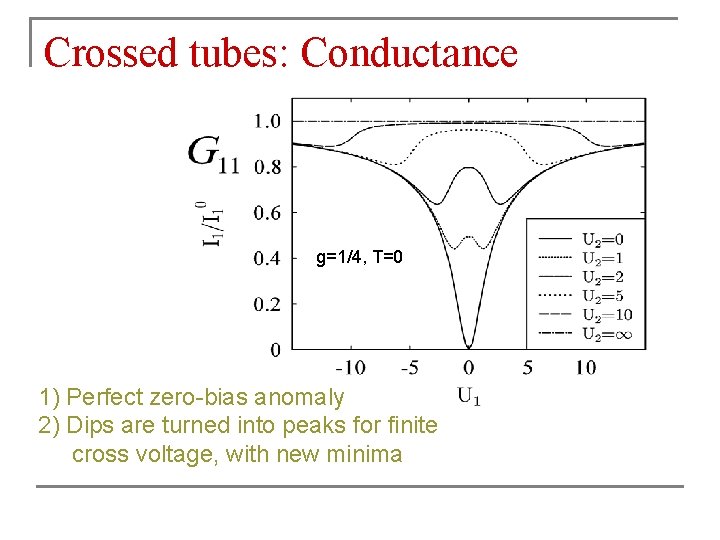
Crossed tubes: Conductance g=1/4, T=0 1) Perfect zero-bias anomaly 2) Dips are turned into peaks for finite cross voltage, with new minima

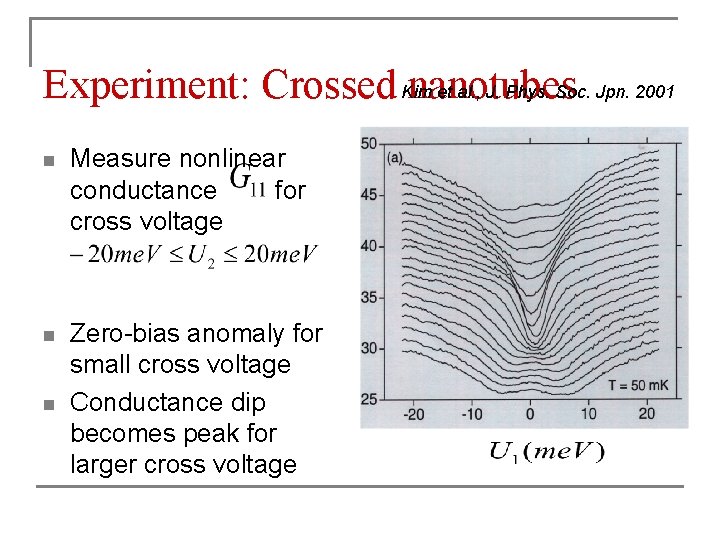
Experiment: Crossed Kim nanotubes et al. , J. Phys. Soc. Jpn. 2001 n Measure nonlinear conductance for cross voltage n Zero-bias anomaly for small cross voltage Conductance dip becomes peak for larger cross voltage n

Coulomb drag: Transconductance n n Strictly local coupling: Linear transconductance always vanishes Finite length: Couplings in +/- sectors differ Now nonzero linear transconductance, except at T=0!

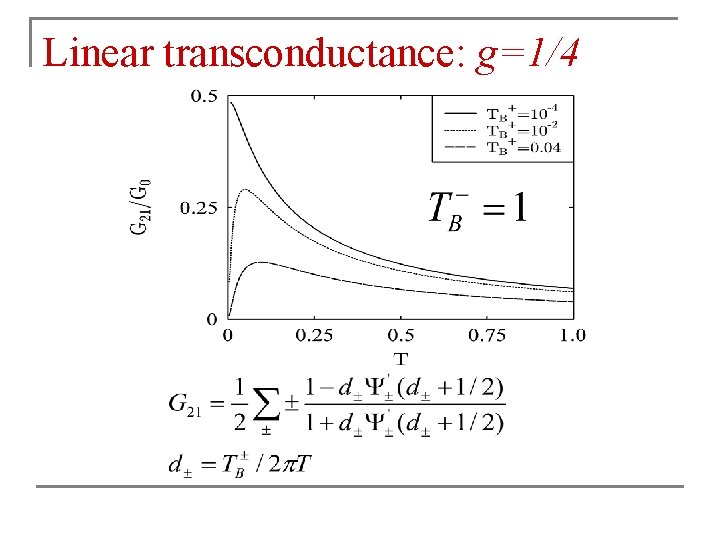
Linear transconductance: g=1/4

Absolute Coulomb drag Averin & Nazarov, PRL 1998 Flensberg, PRL 1998 Komnik & Egger, PRL 1998, EPJB 2001 n For long contact & low temperature: Transconductance approaches maximal value n At zero temperature, linear drag conductance vanishes (in not too long contact)

Coulomb drag shot noise Trauzettel, Egger & Grabert, PRL 2002 n Shot noise at T=0 gives important information beyond conductance n For two-terminal setup, one weak impurity, DC shot noise carries no information about fractional charge n Crossed nanotubes: For must be due to cross voltage (drag noise)

Shot noise transmitted to other tube ? n Mapping to decoupled two-terminal problems implies n Consequence: Perfect shot noise locking q q q Noise in tube 1 due to cross voltage, exactly equal to noise in tube 2 Requires strong interactions, g<1/2 Effect survives thermal fluctuations

Multi-wall nanotubes: Luttinger liquid? n n n Russian doll structure, electronic transport in MWNTs usually in outermost shell only Typically 10 transport bands due to doping Inner shells can create `disorder´ q q Experiments indicate mean free path Ballistic behavior on energy scales

MWNTs: Ballistic limit Egger, PRL 1999 n n Long-range tail of interaction unscreened Luttinger liquid survives in ballistic limit, but Luttinger exponents are closer to Fermi liquid, e. g. End/bulk tunneling exponents are at least one order smaller than in SWNTs Weak backscattering corrections to conductance suppressed as 1/N

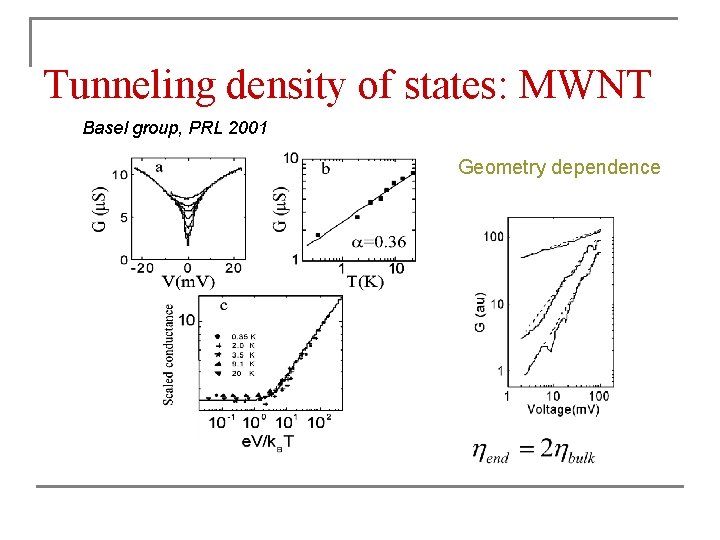
Experiment: TDOS of MWNT n n n DOS observed from conductance through tunnel contact Power law zero-bias anomalies Scaling properties similar to a Luttinger liquid, but: exponent larger than expected from Luttinger theory Bachtold et al. , PRL 2001 (Basel group)

Tunneling density of states: MWNT Basel group, PRL 2001 Geometry dependence

Interplay of disorder and interaction Egger & Gogolin, PRL 2001, Chem. Phys. 2002 Rollbühler & Grabert, PRL 2001 n n n Coulomb interaction enhanced by disorder Microscopic nonperturbative theory: Interacting Nonlinear σ Model Equivalent to Coulomb Blockade: spectral density I(ω) of intrinsic electromagnetic modes

Intrinsic Coulomb blockade n TDOS Debye-Waller factor P(E): n For constant spectral density: Power law with exponent Here: Field/charge diffusion constant

Dirty MWNT n n High energies: Summation can be converted to integral, yields constant spectral density, hence power law TDOS with Tunneling into interacting diffusive 2 D metal Altshuler-Aronov law exponentiates into power law. But: restricted to

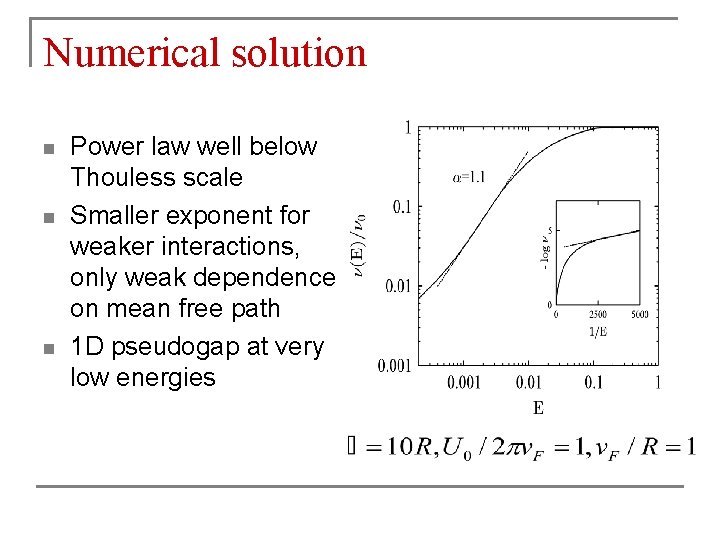
Numerical solution n Power law well below Thouless scale Smaller exponent for weaker interactions, only weak dependence on mean free path 1 D pseudogap at very low energies

Conclusions n n n Luttinger liquid behavior in SWNTs offers new perspectives: Multi-terminal circuits Theory beyond Landauer-Büttiker New fixed points: Broken-up wires, disconnected branches Coulomb drag: Absolute drag, noise locking Multi-wall nanotubes: Interplay disorderinteractions
 Desmosome
Desmosome Classical mechanics
Classical mechanics Quantum physics vs quantum mechanics
Quantum physics vs quantum mechanics Interacting with coworkers
Interacting with coworkers Plasmodesmata
Plasmodesmata Define cell junction
Define cell junction Microfold
Microfold Junction hec ras
Junction hec ras Fusiform fibers smooth muscle
Fusiform fibers smooth muscle Josephson junctions
Josephson junctions Smooth muscle gap junctions
Smooth muscle gap junctions Interacting molecules or ions
Interacting molecules or ions Interacting cognitive subsystems
Interacting cognitive subsystems Antiporter
Antiporter Primary vs secondary active transport
Primary vs secondary active transport Active and passive transport
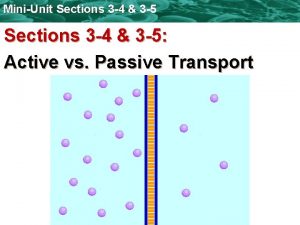
Active and passive transport Advantages of timber conversion
Advantages of timber conversion Now answer the questions
Now answer the questions Passive transport vs active transport venn diagram
Passive transport vs active transport venn diagram Endocytosis vs exocytosis
Endocytosis vs exocytosis Primary active transport vs secondary active transport
Primary active transport vs secondary active transport Bioflix activity membrane transport active transport
Bioflix activity membrane transport active transport Bioflix activity membrane transport diffusion
Bioflix activity membrane transport diffusion Ground live neutral
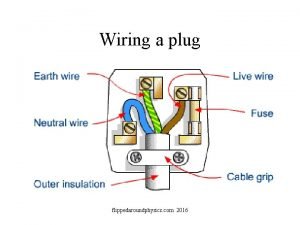
Ground live neutral Live neutral
Live neutral Sin entered through one man
Sin entered through one man Furcation involvement classification
Furcation involvement classification I remember the night my mother
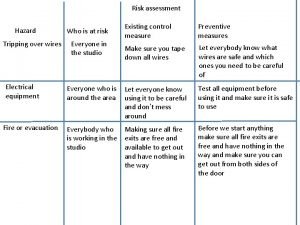
I remember the night my mother Tripping over wires
Tripping over wires 5-1 perpendicular and angle bisectors worksheet
5-1 perpendicular and angle bisectors worksheet A conductor suspended by two flexible wires
A conductor suspended by two flexible wires 2-wires door entry system design
2-wires door entry system design Measuring 45 minutes with two identical wires
Measuring 45 minutes with two identical wires Idiom vs hyperbole
Idiom vs hyperbole Progressive dies
Progressive dies 98 366
98 366 Unit 33 electrical principles and wiring materials
Unit 33 electrical principles and wiring materials Ultra wires
Ultra wires Wires
Wires Two parallel wires
Two parallel wires Two parallel wires
Two parallel wires