Transport Phenomena Shell Momentum Balance Previous Knowledge Definitions

Transport Phenomena Shell Momentum Balance

Previous Knowledge • Definitions – Fluid – Continuum – Steady State flow – Uniform and non uniform • Properties at a point – Density – Stress – Force at point

Previous Knowledge • Molecular Transport of Momentum • Convective Momentum Transport

Topics • • Shell Momentum Balance Boundary conditions Flow of Falling Film Flow through a circular pipe Flow through an annulus Flow through adjacent immiscible flows Creeping flow through a sphere.

Shell Momentum Balance • Volume element • Consist in the establishment of a region in the space, within a specific system, at which the fundamental physical laws are applied to obtain equations to describe the phenomena that occur in the system. • It is a region characterize with a constant volume. • The limit surfaces that limit this volume are called control surfaces.

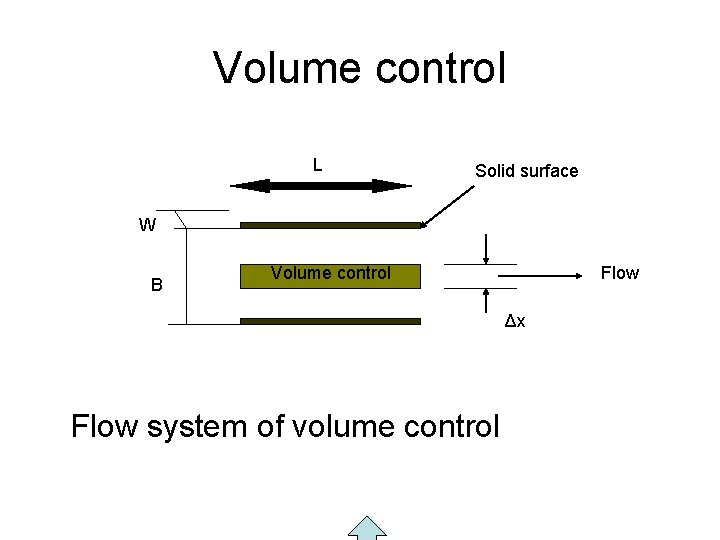
Volume control L Solid surface W B Volume control Flow Δx Flow system of volume control

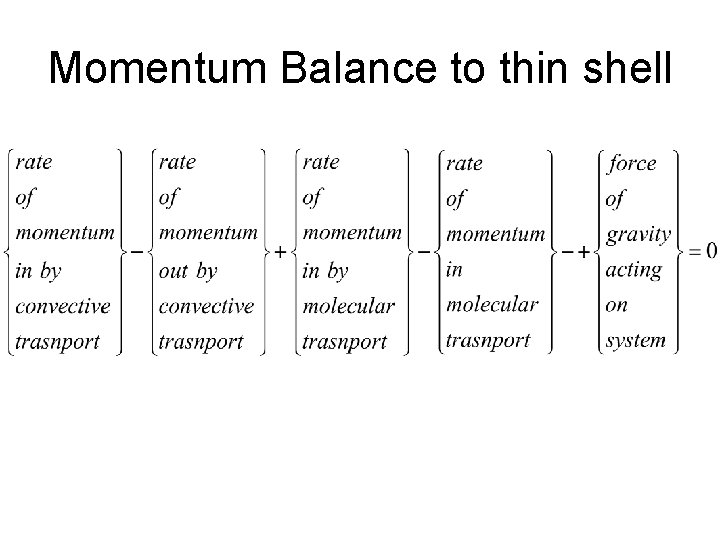
Momentum Balance to thin shell

• This a restricted statement of the law of conservation of momentum • To write the momentum balance we need the expressions for the convective and molecular momentum fluxes given in Table 1. 7. 1 and Table 1. 2 -1(Text book) respectively.

• In summary this general equation can be expressed as

• Flow density – Momentum that entry or exit the system by molecular transport or by global fluid motion. • Sun of forces – Gravity force – Pressure

Procedure to set and solve viscous flow problems • Identify the no vanishing velocity component and the spatial variable on which it depend. • Write a momentum balance over the thin shell perpendicular to the relevant spatial variable. • Let the thickness pf the shell approach zero and make use of the definition of the first derivative to obtain the corresponding differential equation for the momentum flux.

Procedure to set and solve viscous flow problems (Cont. ) • Integrate this equation to get the momentum flux distribution. • Insert Newton’s Law of viscosity and obtain a differential equation for the velocity. • Integrate this equation to get the velocity distribution. • Use the velocity distribution to get other quantities, such as the maximum velocity, average velocity, or force on solid surface.

Boundary conditions • Considerations – There is not material passing through the interface (there is not adsorption, absorption, dissolution, evaporation, melting or chemical reaction at the surface between the two phases.

Boundary conditions • At solid-fluid interfaces • The fluid velocity is equal the velocity with which the solid surface is moving. • This statement is applied to both the tangential and normal component of the velocity vector. • The base of this statement can be found in the roughness of the surface and the adhesion forces between solid and fluid.

Boundary Conditions • At liquid-liquid interfacial plane • The velocity and flux tensor have the same value in both faces. • The flow density (stress-tensor) and the velocity are continuous through the interface

Boundary Conditions • At liquid-gas interfacial plane of constant x, the stress-tensor components are taken to be zero. • The gas side velocity gradient is not too large • The momentum is practically nor being transfer, therefore for calculation purposes can assumed that

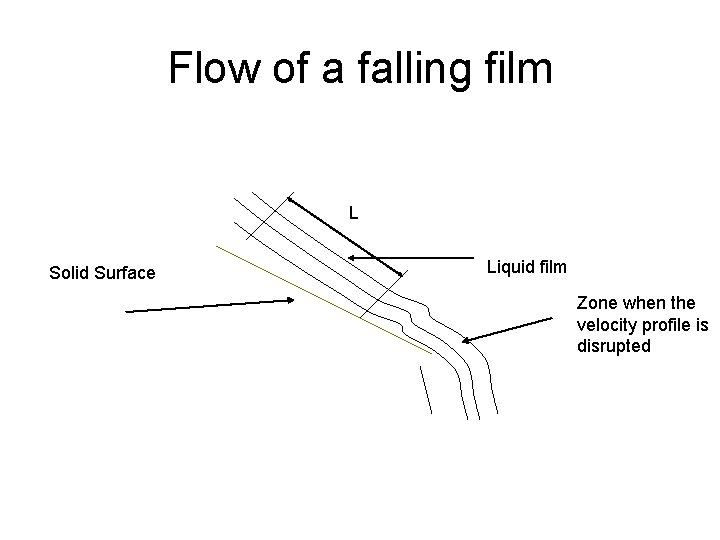
Flow of a falling film L Solid Surface Liquid film Zone when the velocity profile is disrupted

Volume Element for a falling film Momentum In L x Volume element y α Momentum Out Δx Gravity force

Considerations • Isothermal, laminar and stationary flow of a falling film down an inclined flat plane of length L and width B. • The plane is α angle with respect of the gravity force. • Newtonian fluid • The viscosity and density are constant.

Considerations (Cont. ) • The length (L ) is sufficiently small or taken very far from both extreme, therefore the velocity distribution is not affected. • The film has a small thickness δ in x-direction and B in z-direction. • The volume element has a width B and finite thickness Δx. • The force that produce the fluid motion is a component of the gravity force – gy= ρcosα

Considerations (Cont. ) • The direction of the flow is taken in the positive direction of the coordinates axis. • The flow density the entry and exit the volume element is evaluated for at the position with respect to the location of coordinates axis (molecular transport).

Considerations • The flow density the entry and exit the volume due to the bulk of fluid is evaluated at the position with respect to the location of coordinates axis (convective transport). It is represented by ρvyvy. This magnitude is also evaluated for the inlet and outlet points for y = 0 and y = L.

• Applying the general equation of momentum balance and multiplying each term by the magnitude that transform this balance of momentum in force balance

• Terms 3 and 4 are the equal (ρvyvy) in y =0 and y =L. Can be eliminated. • Therefore the equation is

• The left term of the equation by definition is the first derivate of with respect to x, therefore • Integrating

• Applying Boundary Conditions (BC) – Liquid – Gas; x =δ and =0 • Substituting in the previous equation we obtain the Flux tensor distribution equation

Velocity Distribution • Based on the assumption of Newtonian fluid, then

• Applying BC: 2; x = 0 and vy = 0, then C 2=0 • Using this expression we can determine the maximum velocity, average velocity, mass flow rate, film thickness and force of the fluid in the solid surface.

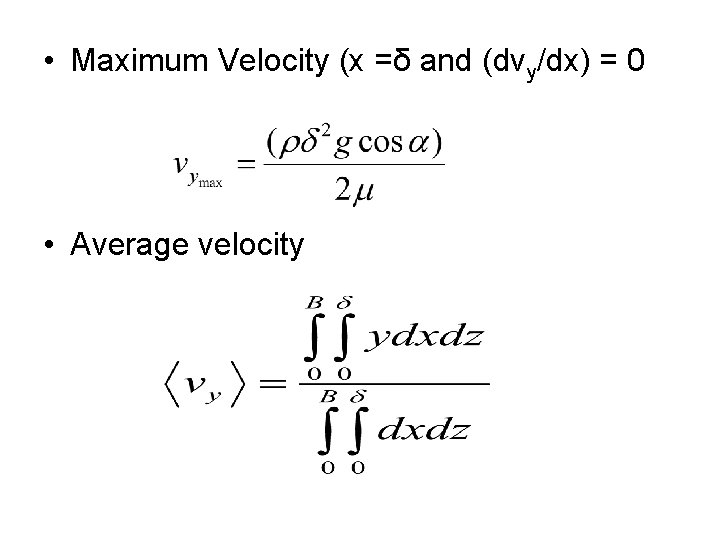
• Maximum Velocity (x =δ and (dvy/dx) = 0 • Average velocity

• Mass flow rate • Force per unit area

END