Transport in weighted networks superhighways and roads Shlomo

Transport in weighted networks: superhighways and roads Shlomo Havlin Bar-Ilan University Israel Collaborators: Z. Wu, Y. Chen, E. Lopez, S. Carmi, L. A. Braunstein, S. Buldyrev, H. E. Stanley Wu, Braunstein, Havlin, Stanley, PRL (2006) Yiping, Lopez, Havlin, Stanley, PRL (2006) Braunstein, Buldyrev, Cohen, Havlin, Stanley, PRL (2003)

What is the research question? • In complex network, different nodes or links have different importance in the transport process. • How to identify the “superhighways”, the subset of the most important links or nodes for transport? • Identifying the superhighways and increasing their capacity enables to improve transport significantly.

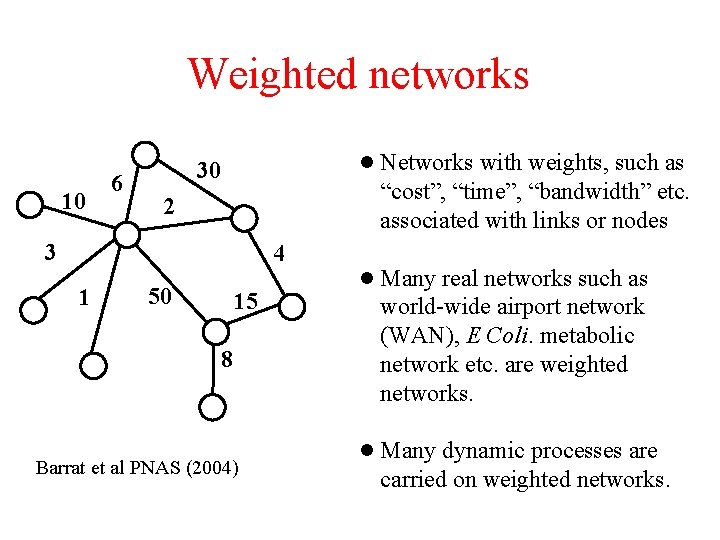
Weighted networks 10 6 l Networks with weights, such as 30 “cost”, “time”, “bandwidth” etc. associated with links or nodes 2 3 4 1 50 15 8 Barrat et al PNAS (2004) l Many real networks such as world-wide airport network (WAN), E Coli. metabolic network etc. are weighted networks. l Many dynamic processes are carried on weighted networks.

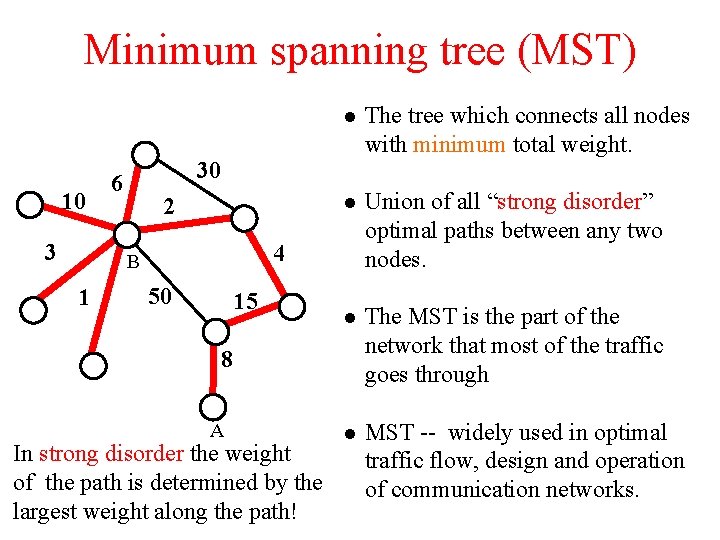
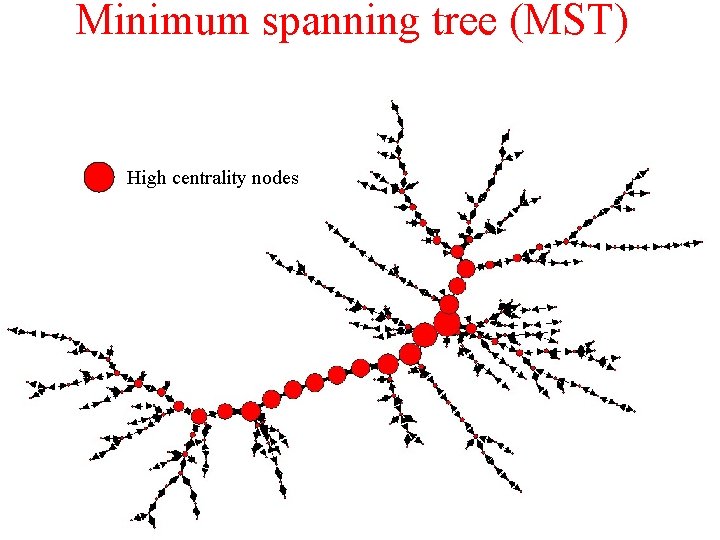
Minimum spanning tree (MST) 10 3 The tree which connects all nodes with minimum total weight. l Union of all “strong disorder” optimal paths between any two nodes. l The MST is the part of the network that most of the traffic goes through l MST -- widely used in optimal traffic flow, design and operation of communication networks. 30 6 2 4 B 1 l 50 15 8 A In strong disorder the weight of the path is determined by the largest weight along the path!

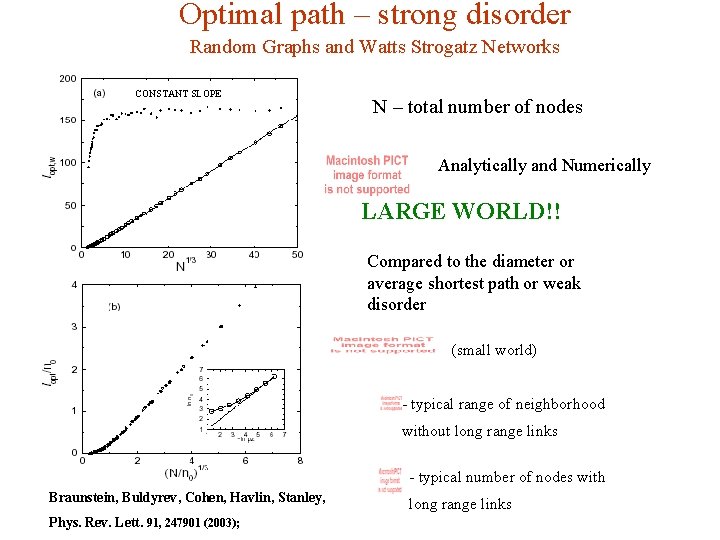
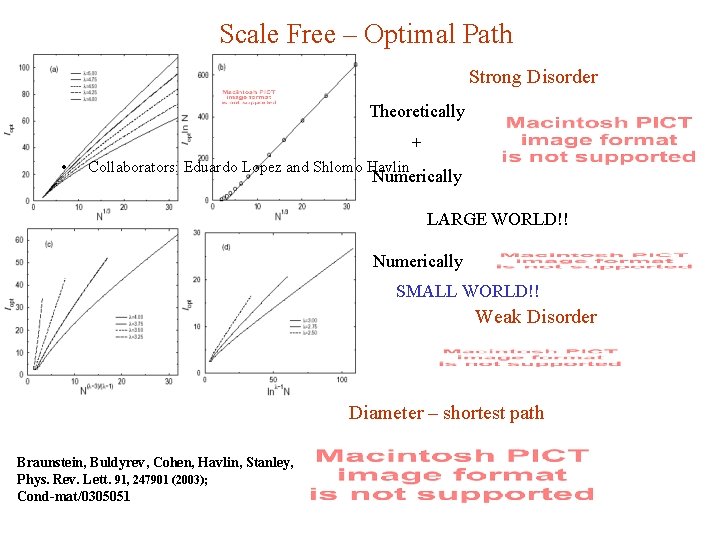
Optimal path – strong disorder Random Graphs and Watts Strogatz Networks CONSTANT SLOPE N – total number of nodes Analytically and Numerically LARGE WORLD!! Compared to the diameter or average shortest path or weak disorder (small world) - typical range of neighborhood without long range links - typical number of nodes with Braunstein, Buldyrev, Cohen, Havlin, Stanley, Phys. Rev. Lett. 91, 247901 (2003); long range links

Betweeness Centrality of MST 0 0 Number of times a node (or link) is used by the set of all shortest paths between all pairs of node. l Measure the frequency of a node being used by traffic. 15 18 12 0 l 7 0 0 Newman. , Phys. Rev. E (2001) D. -H. Kim, et al. , Phys. Rev. E (2004) K. -I. Goh, et al. , Phys. Rev. E (2005) For ER, scale free and real world networks

Minimum spanning tree (MST) High centrality nodes

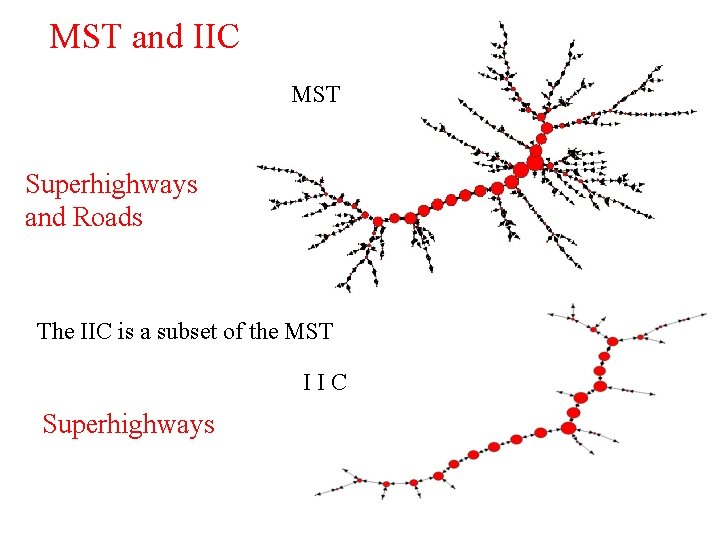
Incipient percolation cluster (IIC) • IIC is defined as the largest component at percolation criticality. • For a random scale-free or Erdös-Rényi graph, to get the IIC, we remove the links in descending order of the weight, until is < 2. At , the system is at criticality. Then the largest connected component of the remaining structure is the IIC. • The IIC can be shown to be a subset of the MST. R. Cohen, et al. , Phys. Rev. Lett. 85, 4626 (2000)

MST and IIC MST Superhighways and Roads The IIC is a subset of the MST IIC Superhighways

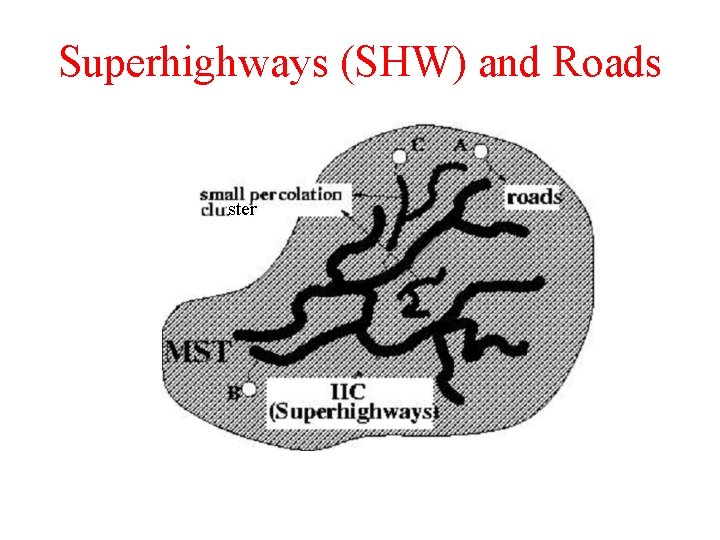
Superhighways (SHW) and Roads ster

Mean Centrality in SHW and Roads

The average fraction of pairs of nodes using the IIC

How much of the IIC is used? Square lattice ER + 3 nd largest cluster ER, + 2 nd largest cluster ER SF, λ= 4. 5 SF, λ= 3. 5 The IIC is only a ZERO fraction of the network of order N 2/3 !!

Distribution of Centrality in MST and IIC

Theory for Centrality Distribution For IIC inside the MST: For the MST: Good agreement with simulations!

Application: improve flow in the network Comparison between two strategies: s. I: improving capacity of all IIC links--highways s. II: improving the highest centrality links in MST (same number as s. I). Assume: multiple sources and sinks: randomly choose n pairs of nodes as sources and other n nodes as sinks We study two transport problems: • Current flow in random resistor networks, where each link of the network represents a resistor. (Total flow, F: total current or conductance) • Maximum flow problem from computer science, where each link of the network has an upper bound capacity. (Total flow, F: maximum possible flow into network) Result: s. I is better

Application: compare two strategies current flow and maximum flow n=50 n=250 n=500 s. I: improve the IIC links. s. II: improve the high C links in MST. Two types of transport • Current flow: improve the conductance • Maximum flow: improve the capacity F 0: flow of original network. Fs. I : flow after using s. I. Fs. II: flow after using s. II. N=2048, <k>=4

Summary • . MST can be partitioned into superhighways which carry most of the traffic and roads with less traffic. • We identify the superhighways as the largest percolation cluster at criticality -- IIC. • Increasing the capacity of the superhighways enables to improve transport significantly. The superhighways of order N 2/3 -- a zero fraction of the network!!

Applications: compare 2 strategies current flow and maximum flow Two transport problems: • Current flow in random resistor networks, where each link of the network represents a resistor. (Total flow, F: total current or conductance) • Maximum flow problem in computer science[4], where each link of the network has a capacity upper bound. (Total flow, F: maximum possible flow into network) resistance/capacity = eax, with a = 40 (strong disorder) Multiple sources and sinks: randomly choose n pairs of nodes as sources and other n nodes as sinks Two strategies to improve flow, F, of the network: s. I: improving the IIC links. s. II: improving the high C links in MST. [4]. Using the push-relabel algorithm by Goldberg. http: //www. avglab. com/andrew/soft. html

Universal behavior of optimal paths in weighted networks with general disorder Yiping Chen Advisor: H. E. Stanley Y. Chen, E. Lopez, S. Havlin and H. E. Stanley “Universal behavior of optimal paths in weighted networks with general disorder” PRL(submitted)

Scale Free – Optimal Path Strong Disorder Theoretically + • Collaborators: Eduardo Lopez and Shlomo Havlin Numerically LARGE WORLD!! Numerically SMALL WORLD!! Weak Disorder Diameter – shortest path Braunstein, Buldyrev, Cohen, Havlin, Stanley, Phys. Rev. Lett. 91, 247901 (2003); Cond-mat/0305051

Motivation: Different disorders are introduced to mimic the individual properties of links or nodes (distance, airline capacity…).

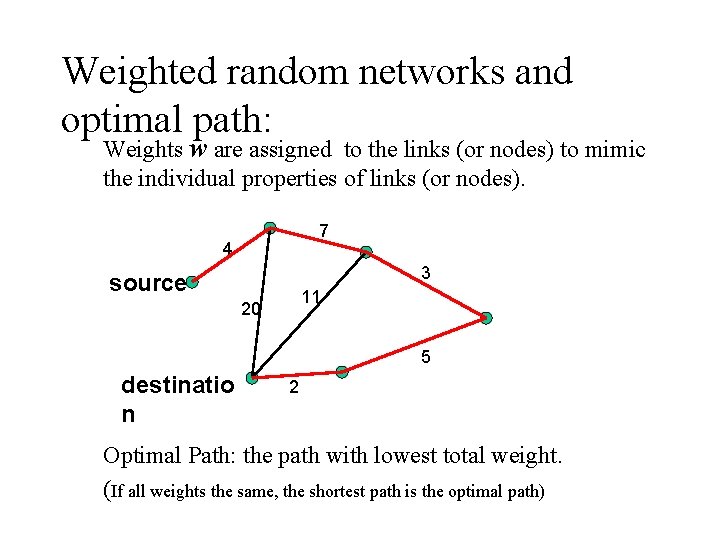
Weighted random networks and optimal path: Weights w are assigned to the links (or nodes) to mimic the individual properties of links (or nodes). 7 4 3 source 11 20 5 destinatio n 2 Optimal Path: the path with lowest total weight. (If all weights the same, the shortest path is the optimal path)

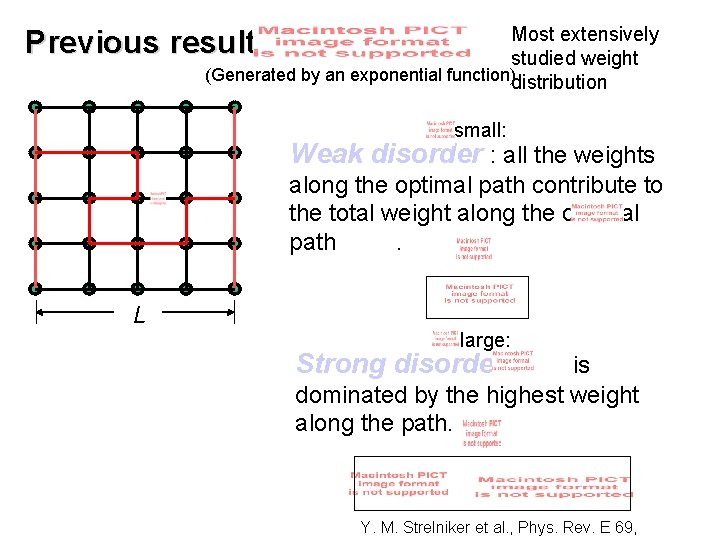
Most extensively studied weight (Generated by an exponential function)distribution Previous results: small: Weak disorder : all the weights along the optimal path contribute to the total weight along the optimal path. L large: Strong disorder : is dominated by the highest weight along the path. Y. M. Strelniker et al. , Phys. Rev. E 69,

Unsolved problem: General weight distribution Needed to reflect the properties of real world. Ex: • exponential function----quantum tunnelling effect • power-law----diffusion in random media • lognormal----conductance of quantum dots • Gaussian----polymers

Questions: Do optimal paths for different weight distributions show similar behavior? 1. 2. Is it possible to derive a way to predict whether the weighted network is in strong or weak disorder in case of general weight distribution? 3. Will strong disorder behavior show up for any distributions when distribution is broad?

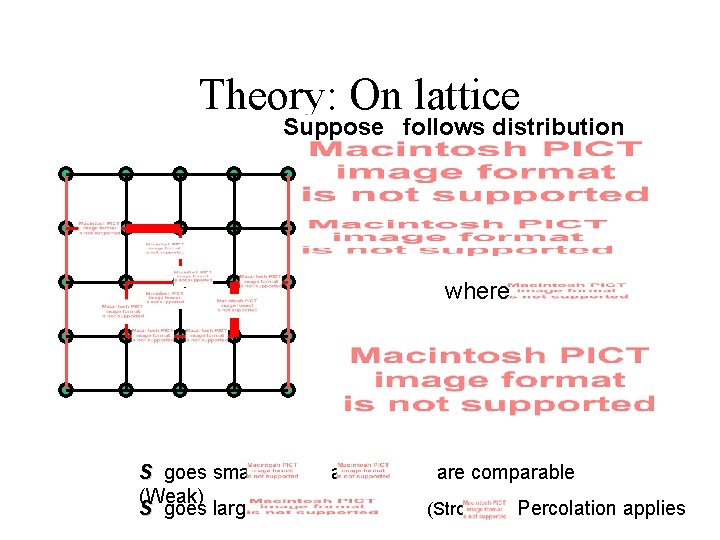
Theory: On lattice Suppose the weight follows distribution (Total cost) where We define 0: , cannot dominate the total cost (Weak limit) 1: , L dominates the total cost (Strong limit) Assume S can determine the strong or weak Using percolation theory: behavior. Structural & distributional parameter Percolation exponent

General distributions studied in simulation • Power-law with additional parameter • Lognormal • Gaussian

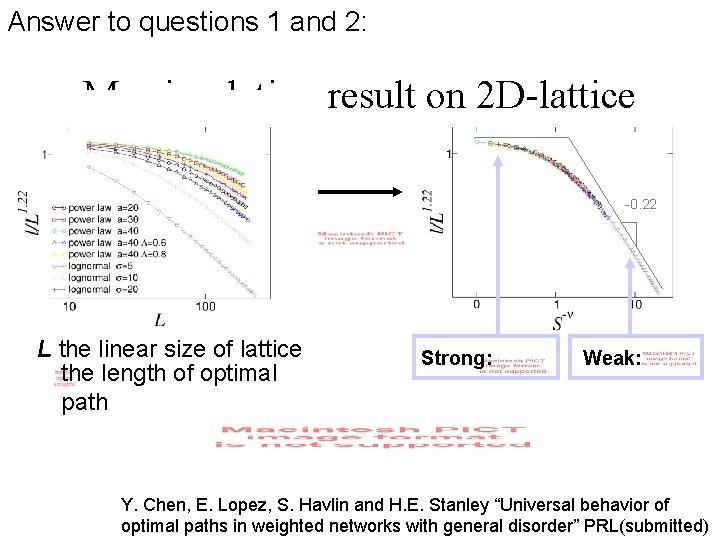
Answer to questions 1 and 2: My simulation result on 2 D-lattice -0. 22 L the linear size of lattice the length of optimal path Strong: Weak: Y. Chen, E. Lopez, S. Havlin and H. E. Stanley “Universal behavior of optimal paths in weighted networks with general disorder” PRL(submitted)

Erdős-Rényi (ER) Networks Definition: For each pair of nodes, they have probability p to be connected A set of N nodes p My simulations on ER network show the same agreement with theory.

Answer to question 3: Distributions that are not expected to have strong disorder behavior • Gaussian • Exponential ( the percolation threshold, constant for certain network structure) A is independent of which describes the broadness of distribu No matter how broad the distribution is, not be large, and no strong disorder will show up. can

Summary of answers to 3 questions 1. Do optimal paths in different weight distributions show similar behavior? Yes 2. Is it possible to derive a way to predict whether the weighted network is in strong or weak disorder in case of general weight distribution? Yes 3. Will strong disorder behavior show up for any distributions when distribution is broad?

Theory: On lattice Suppose follows distribution where S goes small: (Weak) S goes large: and are comparable (Strong) Percolation applies

Percolation Theory Percolation properties: Percolation threshold (0. 5 for 2 D square In finite lattice with linear size L: lattice) The Strong first and second highest disorder and weighted bonds in optimal path will percolation behave be close to and follow in its the similar way deviation rule. Thus

From percolation theory The result comes from percolation theory Transfer back to original disorder distribution

Test on known result Apply our theory on disorder distribution , we get percolation threshold (Constants for certain percolation structure) exponent In 2 D square lattice To have same behavior by keeping fixed, we get constant Compatible with the reported results. (The crossover from strong to weak disorder occurs at

Scaling on ER network Percolation at criticality on Erdős-Rényi(ER) networks is equivalent to percolation on a lattice at the upper critical dimension. (N = number of nodes) Virtual linear size Percolation exponent in ER network ( is now depending on number of nodes in ER network)

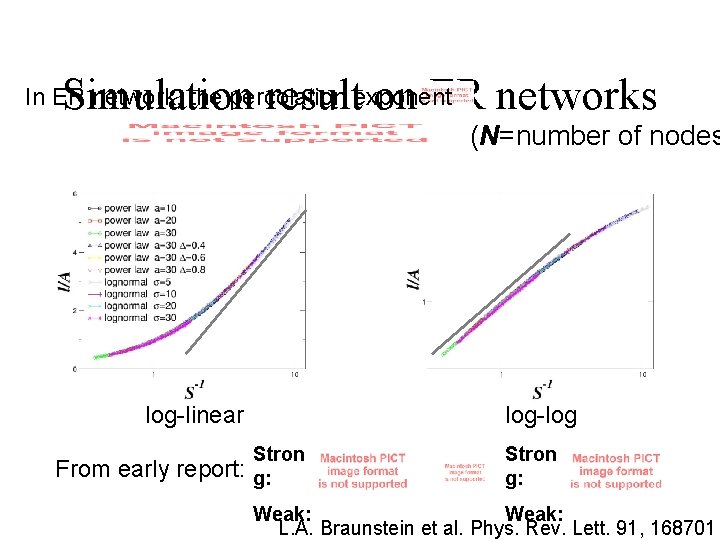
Simulation result on ER networks In ER network, the percolation exponent (N=number of nodes log-linear From early report: log-log Stron g: Weak: L. A. Braunstein et al. Phys. Rev. Lett. 91, 168701