Transmission Line Properties Has two conductors running parallel

Transmission Line Properties § Has two conductors running parallel § Can propagate a signal at any frequency (in theory) § Becomes lossy at high frequency § Can handle low or moderate amounts of power § Does not have signal distortion, unless there is loss § May or may not be immune to interference § Does not have Ez or Hz components of the fields (TEMz) Coaxial cable (coax) Twin lead (shown connected to a 4: 1 impedance-transforming balun) 1

Transmission Line (cont. ) CAT 5 cable (twisted pair) The two wires of the transmission line are twisted to reduce interference and radiation from discontinuities. 2

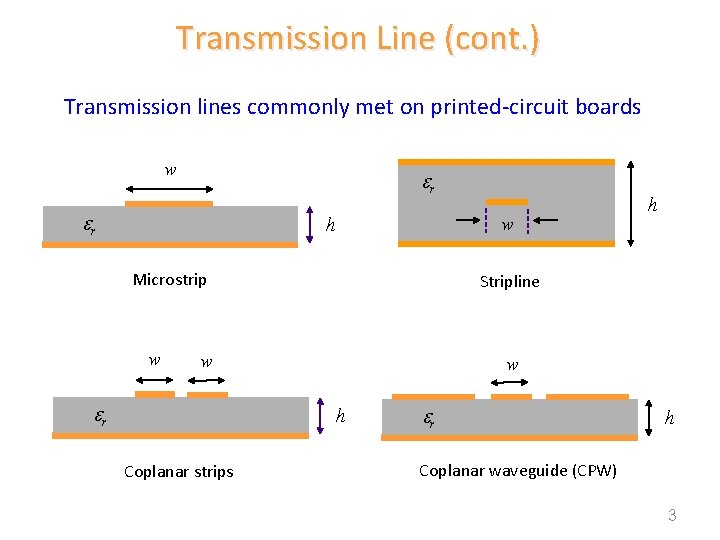
Transmission Line (cont. ) Transmission lines commonly met on printed-circuit boards w r r h w Microstrip w Stripline w r w h Coplanar strips h r h Coplanar waveguide (CPW) 3

Transmission Line (cont. ) Transmission lines are commonly met on printed-circuit boards. Microstrip line A microwave integrated circuit 4

Fiber-Optic Guide Properties § Uses a dielectric rod § Can propagate a signal at any frequency (in theory) § Can be made very low loss § Has minimal signal distortion § Very immune to interference § Not suitable for high power § Has both Ez and Hz components of the fields 5

Fiber-Optic Guide (cont. ) Two types of fiber-optic guides: 1) Single-mode fiber Carries a single mode, as with the mode on a transmission line or waveguide. Requires the fiber diameter to be small relative to a wavelength. 2) Multi-mode fiber Has a fiber diameter that is large relative to a wavelength. It operates on the principle of total internal reflection (critical angle effect). 6

Fiber-Optic Guide (cont. ) Higher index core region http: //en. wikipedia. org/wiki/Optical_fiber 7

Properties Waveguides § Has a single hollow metal pipe § Can propagate a signal only at high frequency: > c § The width must be at least one-half of a wavelength § Has signal distortion, even in the lossless case § Immune to interference § Can handle large amounts of power § Has low loss (compared with a transmission line) § Has either Ez or Hz component of the fields (TMz or TEz) http: //en. wikipedia. org/wiki/Waveguide_(electromagnetism) 8

Transmission-Line Theory § Lumped circuits: resistors, capacitors, inductors neglect time delays (phase) § Distributed circuit elements: transmission lines account for propagation and time delays (phase change) We need transmission-line theory whenever the length of a line is significant compared with a wavelength. 9

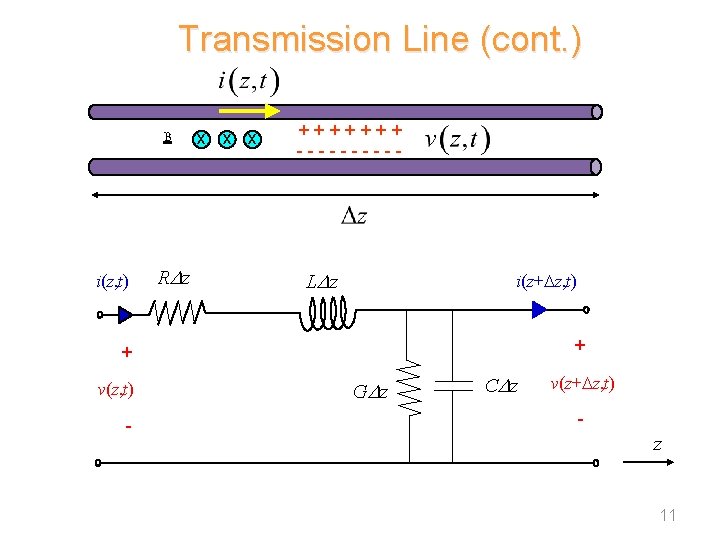
Transmission Line 2 conductors 4 per-unit-length parameters: C = capacitance/length [F/m] L = inductance/length [H/m] R = resistance/length [ /m] G = conductance/length [ /m or S/m] Dz 10

Transmission Line (cont. ) B i(z, t) RDz x x x +++++++ ----- LD z i(z+ z, t) + + v(z, t) - GD z CDz v(z+ z, t) - z 11

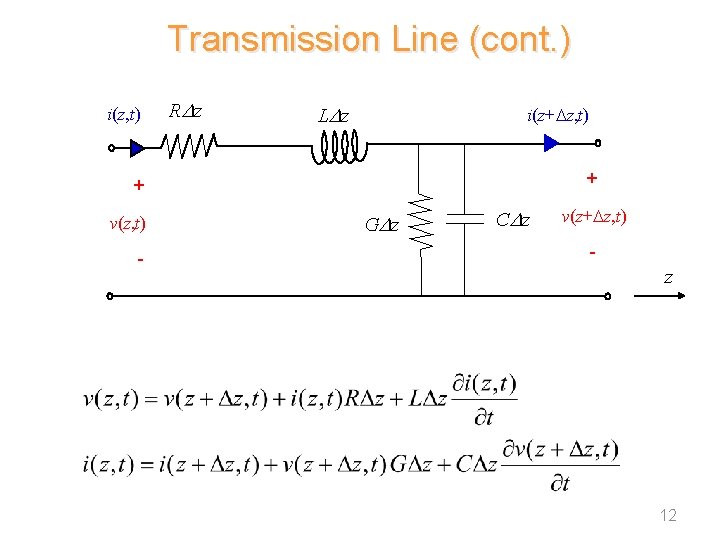
Transmission Line (cont. ) i(z, t) RDz LD z i(z+ z, t) + + v(z, t) - GD z CDz v(z+ z, t) - z 12

TEM Transmission Line (cont. ) Hence Now let z 0: “Telegrapher’s Equations” 13

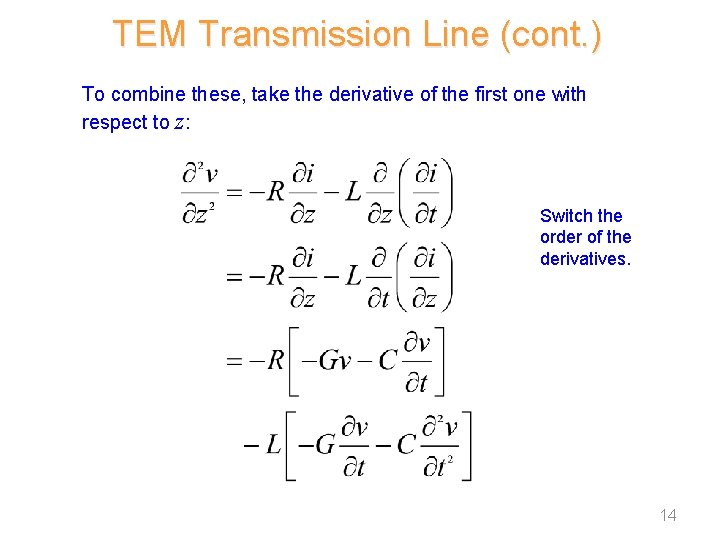
TEM Transmission Line (cont. ) To combine these, take the derivative of the first one with respect to z: Switch the order of the derivatives. 14

TEM Transmission Line (cont. ) Hence, we have: The same equation also holds for i. 15

TEM Transmission Line (cont. ) Time-Harmonic Waves: 16

TEM Transmission Line (cont. ) Note that = series impedance/length = parallel admittance/length Then we can write: 17

TEM Transmission Line (cont. ) Let Then Solution: is called the "propagation constant. " Convention: 18

TEM Transmission Line (cont. ) Forward travelling wave (a wave traveling in the positive z direction): The wave “repeats” when: Hence: 19

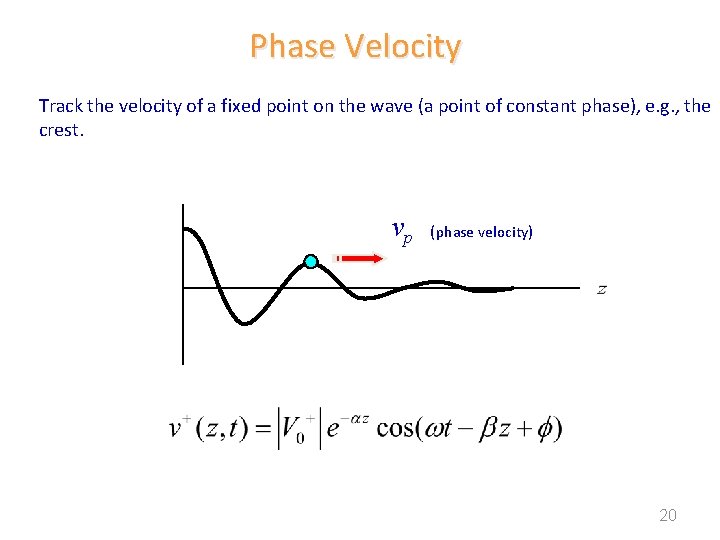
Phase Velocity Track the velocity of a fixed point on the wave (a point of constant phase), e. g. , the crest. vp (phase velocity) 20

Phase Velocity (cont. ) Set In expanded form: Hence 21

Characteristic Impedance Z 0 I+ (z) + V+(z) - z A wave is traveling in the positive z direction. so (Z 0 is a number, not a function of z. ) 22

Characteristic Impedance Z 0 (cont. ) Use Telegrapher’s Equation: so Hence 23

Characteristic Impedance Z 0 (cont. ) From this we have: Using We have Note: The principal branch of the square root is chosen, so that Re (Z 0) > 0. 24

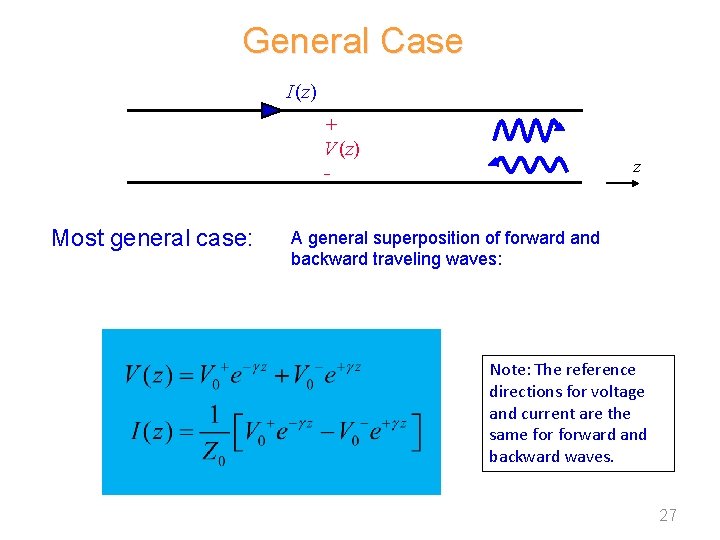
General Case (Waves in Both Directions) Note: wave in +z direction wave in -z direction 25

Backward-Traveling Wave I - (z) + V -(z) - z A wave is traveling in the negative z direction. so Note: The reference directions for voltage and current are the same as for the forward wave. 26

General Case I (z) + V (z) - Most general case: z A general superposition of forward and backward traveling waves: Note: The reference directions for voltage and current are the same forward and backward waves. 27

Summary of Basic TL formulas guided wavelength g phase velocity vp 28

Lossless Case so (real and indep. of freq. ) (indep. of freq. ) 29

Lossless Case (cont. ) In the medium between the two conductors is homogeneous (uniform) and is characterized by ( , ), then we have that (proof given later) The speed of light in a dielectric medium is Hence, we have that The phase velocity does not depend on the frequency, and it is always the speed of light (in the material). 30

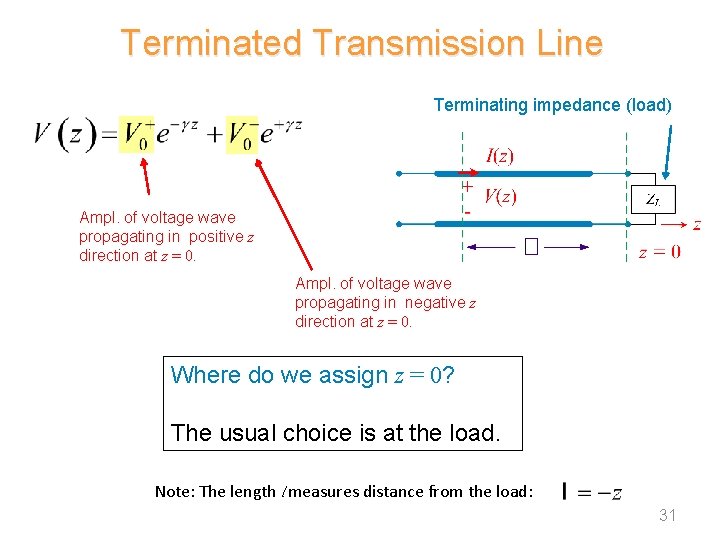
Terminated Transmission Line Terminating impedance (load) Ampl. of voltage wave propagating in positive z direction at z = 0. Ampl. of voltage wave propagating in negative z direction at z = 0. Where do we assign z = 0? The usual choice is at the load. Note: The length l measures distance from the load: 31

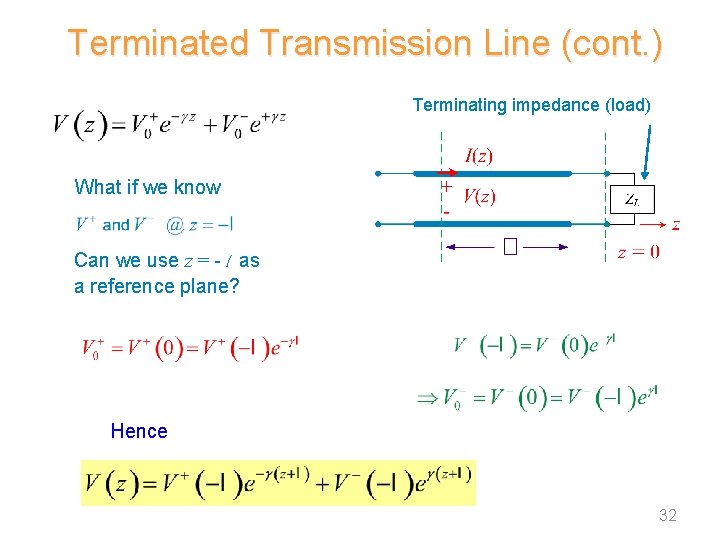
Terminated Transmission Line (cont. ) Terminating impedance (load) What if we know Can we use z = - l as a reference plane? Hence 32

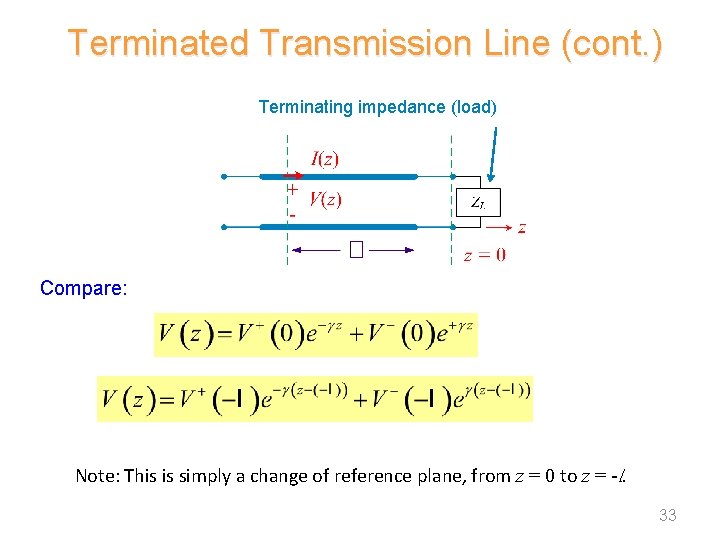
Terminated Transmission Line (cont. ) Terminating impedance (load) Compare: Note: This is simply a change of reference plane, from z = 0 to z = -l. 33

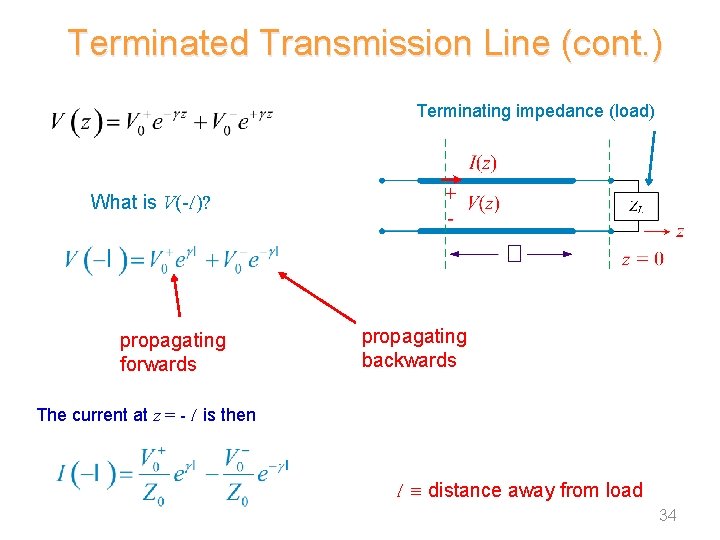
Terminated Transmission Line (cont. ) Terminating impedance (load) What is V(-l )? propagating forwards propagating backwards The current at z = - l is then l distance away from load 34

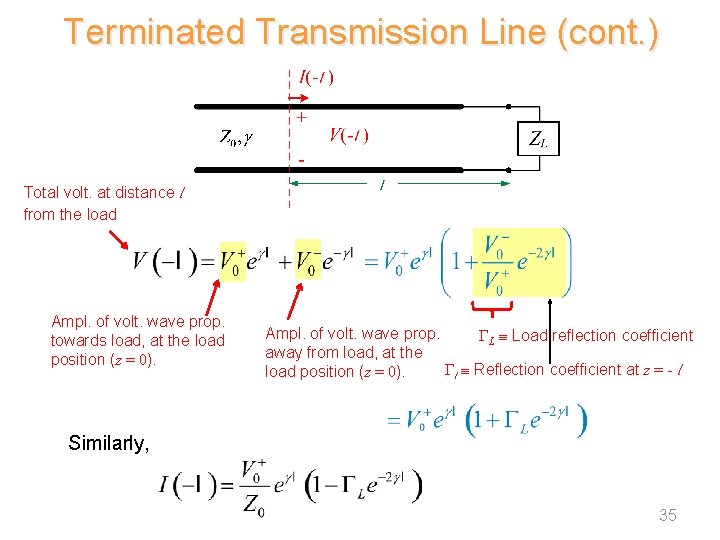
Terminated Transmission Line (cont. ) Total volt. at distance l from the load Ampl. of volt. wave prop. towards load, at the load position (z = 0). Ampl. of volt. wave prop. L Load reflection coefficient away from load, at the l Reflection coefficient at z = - l load position (z = 0). Similarly, 35

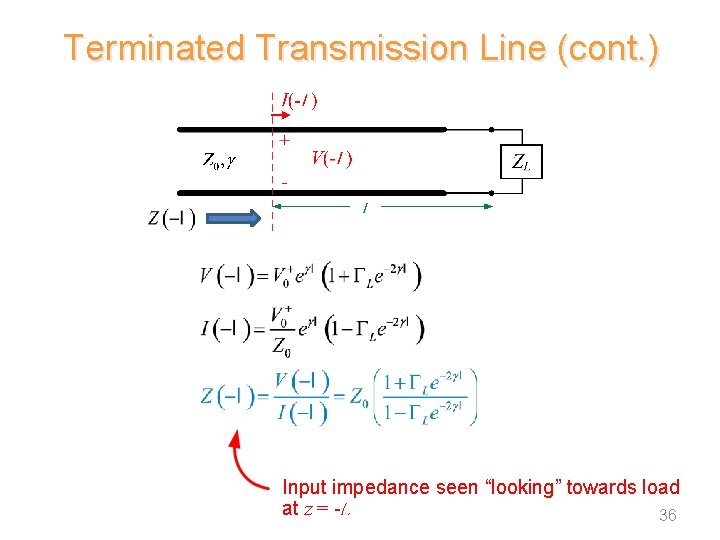
Terminated Transmission Line (cont. ) Input impedance seen “looking” towards load at z = -l. 36

Terminated Transmission Line (cont. ) At the load (l = 0): Recall Thus, 37

Terminated Transmission Line (cont. ) Simplifying, we have Hence, we have 38

Terminated Lossless Transmission Line Impedance is periodic with period g/2 tan repeats when Note: 39

Terminated Lossless Transmission Line For the remainder of our transmission line discussion we will assume that the transmission line is lossless. 40

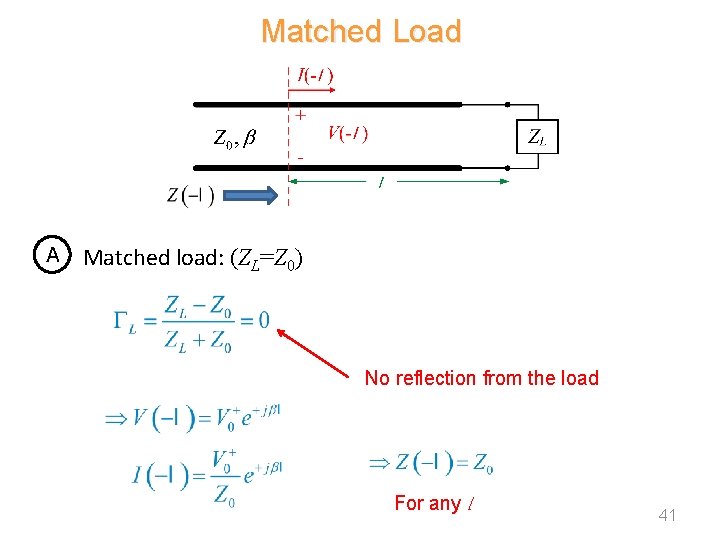
Matched Load A Matched load: (ZL=Z 0) No reflection from the load For any l 41

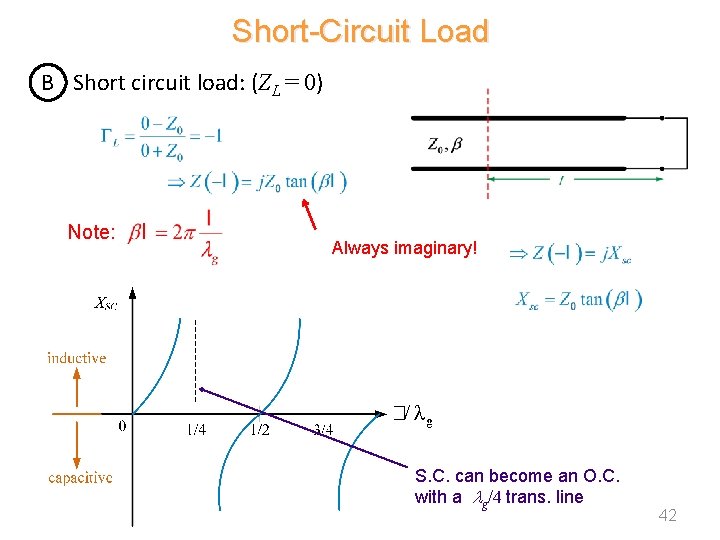
Short-Circuit Load B Short circuit load: (ZL = 0) Note: Always imaginary! S. C. can become an O. C. with a g/4 trans. line 42

Using Transmission Lines to Synthesize Loads This is very useful is microwave engineering. A microwave filter constructed from microstrip. 43

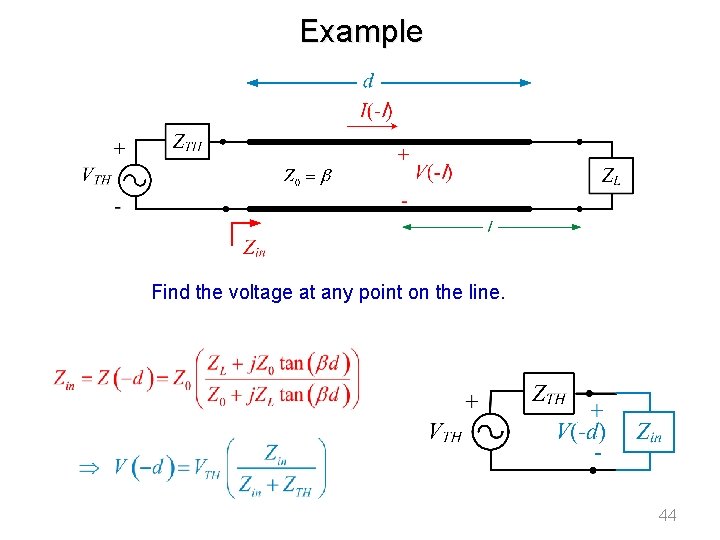
Example Find the voltage at any point on the line. 44

Example (cont. ) Note: At l = d : Hence 45

Example (cont. ) Some algebra: 46

Example (cont. ) Hence, we have where Therefore, we have the following alternative form for the result: 47

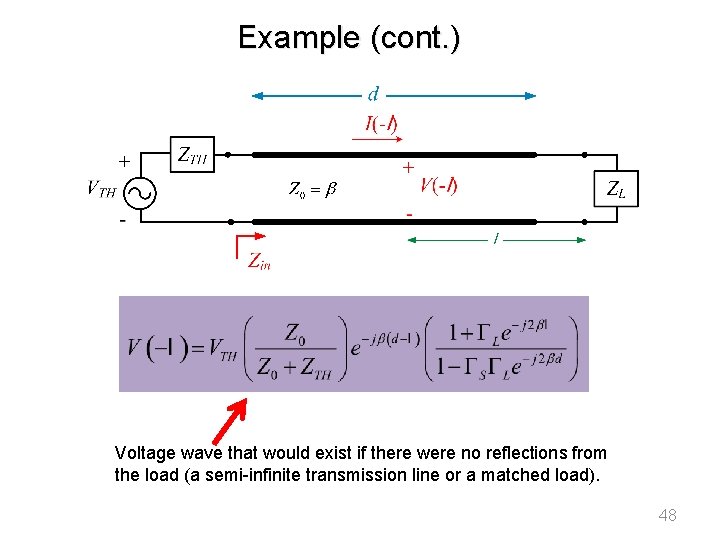
Example (cont. ) Voltage wave that would exist if there were no reflections from the load (a semi-infinite transmission line or a matched load). 48

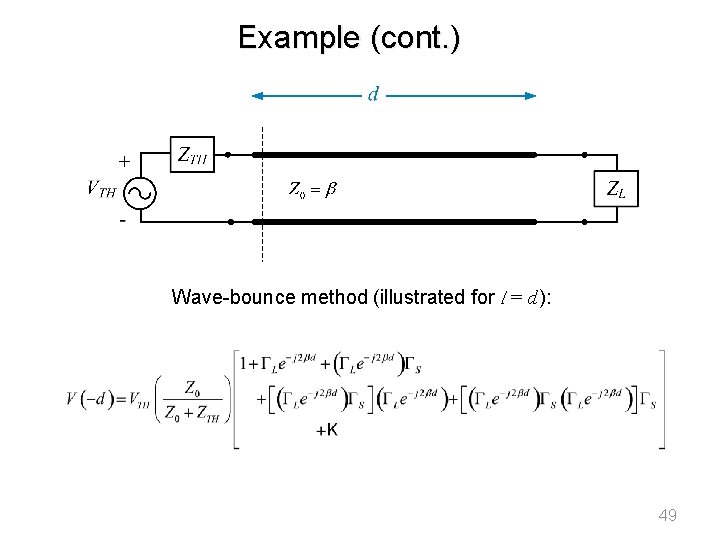
Example (cont. ) Wave-bounce method (illustrated for l = d ): 49

Example (cont. ) Geometric series: 50

Example (cont. ) Hence or This agrees with the previous result (setting l = d ). Note: This is a very tedious method – not recommended. 51

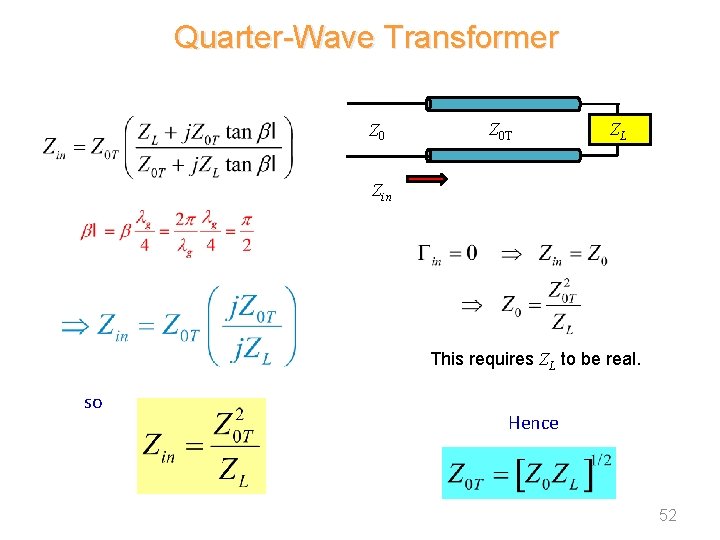
Quarter-Wave Transformer Z 0 T ZL Zin This requires ZL to be real. so Hence 52

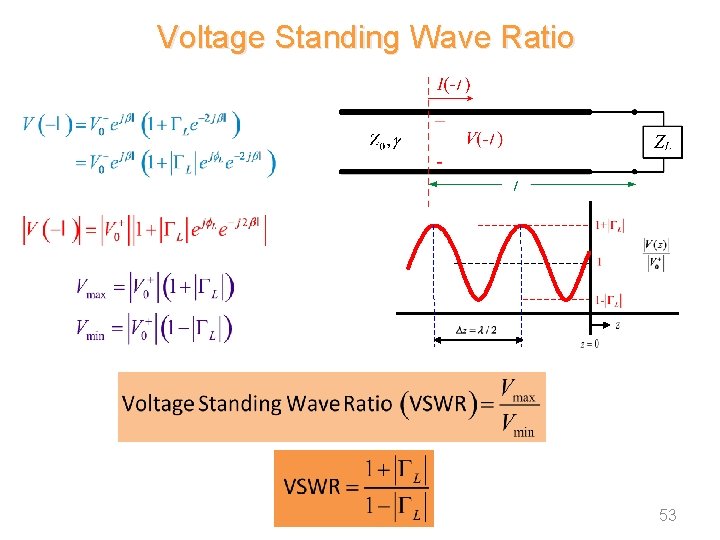
Voltage Standing Wave Ratio 53