Transmission Line Problems EEE 211 Cont cont Cont

Transmission Line Problems EEE 211

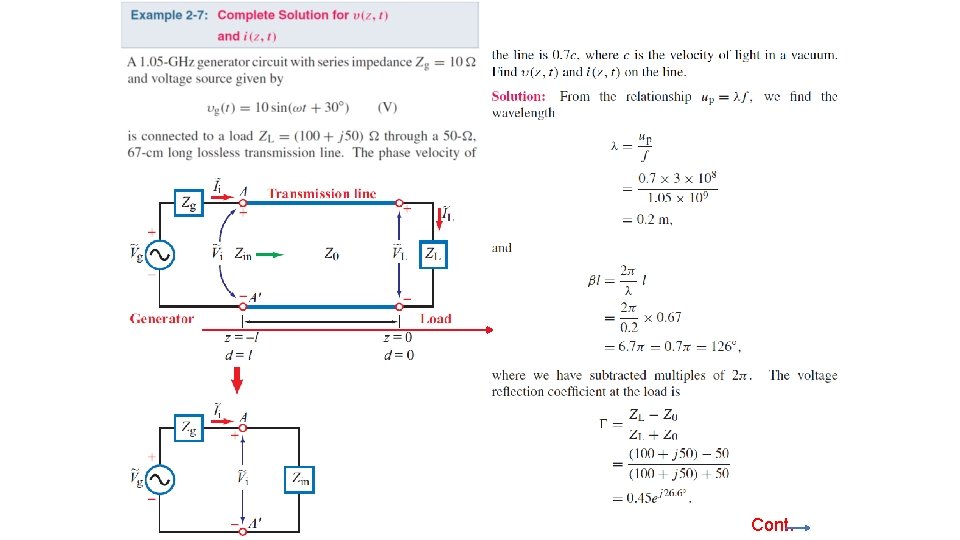
Cont.

(cont. ) Cont.

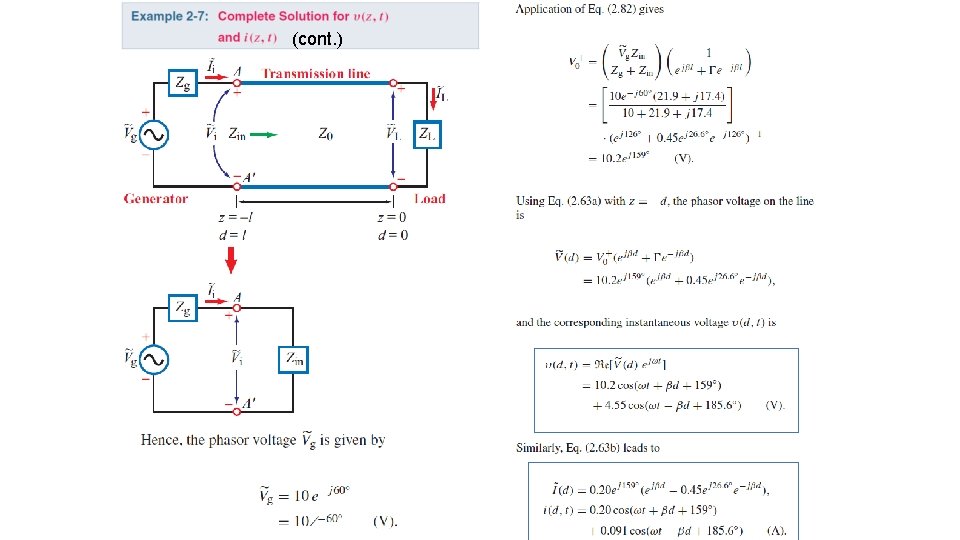
(cont. )

Equations summary

Input Impedance

Forward voltage

Misc

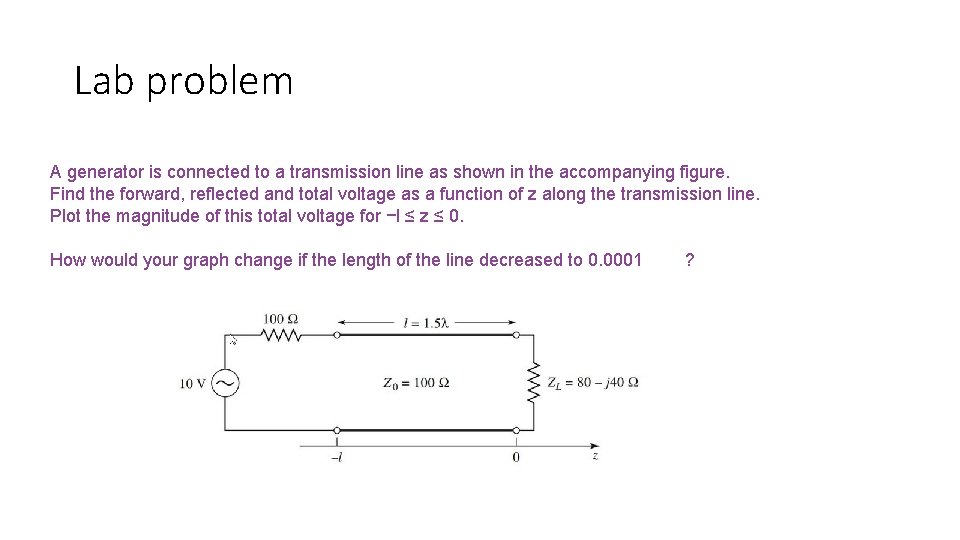
Lab problem A generator is connected to a transmission line as shown in the accompanying figure. Find the forward, reflected and total voltage as a function of z along the transmission line. Plot the magnitude of this total voltage for −l ≤ z ≤ 0. How would your graph change if the length of the line decreased to 0. 0001 ?

Lab Intro to TL problem • Use the phasor equation for voltage and current on a shorted transmission line to draw a vector phasor diagram of voltage and current at 5 different points on the line: z=0, z=-λ/8, z=-λ/4, z=-3λ/8, z=-λ/2 • Then by looking at the total voltage and current on the line find whether the impedance at these points is a short, open, inductive or capacitive.

Angle of input reflection coefficient

Objective • Students will be able to • explain why is the impedance matching needed • How real power changes from the input to the output of a lossless transmission line • What is the requirement for maximum available power from the generator? • What is the requirement for the minimum reflected power from the load?

Why do we look at power transfer at RF? • At lower frequencies we look at voltage gain or current gain • At Radio Frequencies (RF) we look at the power transfer • At low frequencies the voltage at one end of a cable is the same as the voltage at the other side of the cable • At RF the voltage at the input of the cable is not the same as the voltage at the output, BUT: the delivered power at the input port is the same as the power delivered to the load (no power is dissipated in reactive elements)

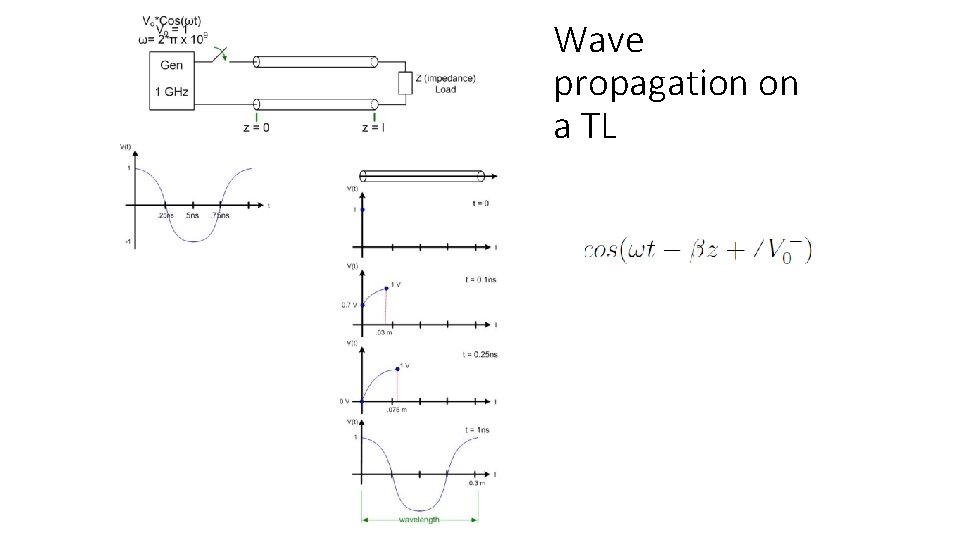
Wave propagation on a TL

Impedance matching • We need to maximize power transfer between source and the load • Maximum power transfer occurs when the impedance of the load and the generator are complex conjugate of each other. • This maximizes V

Instantaneous Power Flow

Average Power

Conjugate match maximizes ZL=Zo Minimizes reflection

Incident, Reflected and Delivered Power • Seemingly, we have two requirements: • 1) • 2) For maximum power transfer To minimize reflected power What is the input impedance Zin=? if ZL=Zo? Look at the Smith Chart. Where is ZL (normalized)?

Incident, Reflected and Absorbed Power • Seemingly, we have two requirements: • 1) • 2) Maximizes Minimizes Available power from the generator • When Zl=Zo, and Zg=Zo, then we have the best of both worlds!

Graded Quiz TL#3 A transmitter operated at 20 MHz, Vg=100 V with 50Ω internal impedance is connected to an antenna load through 6. 33 m of the line. The line is a lossless 50Ω, β=0. 595 rad/m. The antenna impedance at 20 MHz measures ZL=36+j 20 Ω. a) What is the electrical length of the line? (length=0. 6 λ ) b) How much power is delivered to the line? Hint: Find the input impedance, then Pav, in=1/2 Re{Vin (Iin)*}=1/2 Re{Zin Iin (Iin)*}=1/2 Rin|Iin|^2 c) What is the time-average power absorbed by ZL? PL 1/2 Rl |IL|^2 d) If Zl is matched to 50 Ohm line, what is the input impedance of the line, and how much average power is delivered to the line and load?

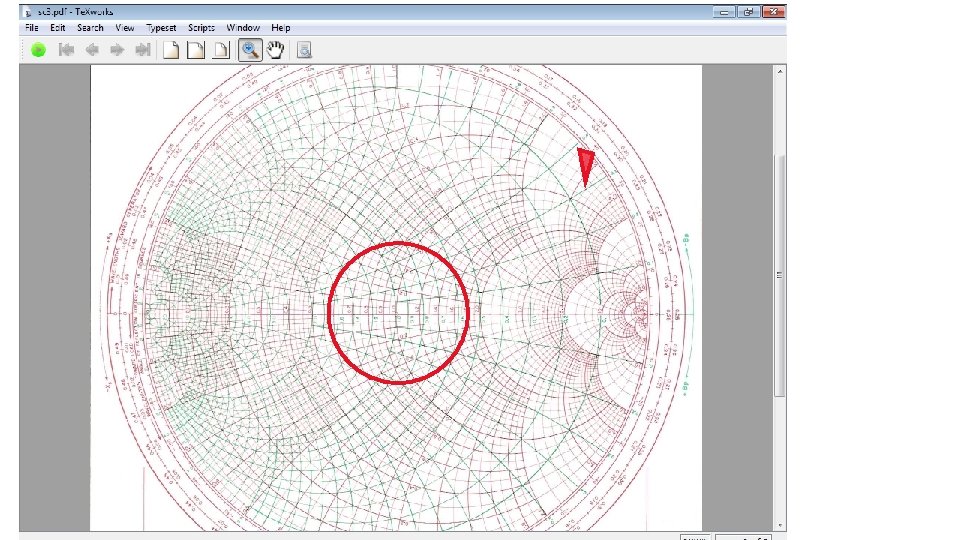
At the load z=0

Answers Note that the “real” power at the load and the “real” power at the generator are the same.