Translations Translation a transformation that slides an object

Translations Translation - a transformation that slides an object in a straight line without changing its size or orientation. A translation "slides" an object a fixed distance in a given direction. The original object and its translation have the same shape and size, and they face in the same direction. A translation creates a figure that is similar to the original and preserves length and orientation. To make a translation we have two main ways to indicate the translation: Description: Describes the movement, how much the figure moves up or down and how far it is moved left to right. Using a mapping rule where we take the original point (i. e. A, B, C) and convert it to the final image (i. e. A’, B’, C’).

MAPPING RULE: (x, y) where (x + a, y + b) a = units left/right b= units up/down Example: Take triangle ABC and translate it, 2 units down and 6 units to the right. Using the mapping rule: (x, y) (x + 6, y – 2) This moves each point for x point 6 places to the right, and each y point 2 units down Point A (-5, 4) – Point A’ = (-5+6, 4 -2) = (1, 2) Point B (-2, 4) – Point B’ = (-2+6, 4 -2) = (4, 2) Point C (-2, 2) – Point C’ = (-2+6, 2 -2) = (4, 0)

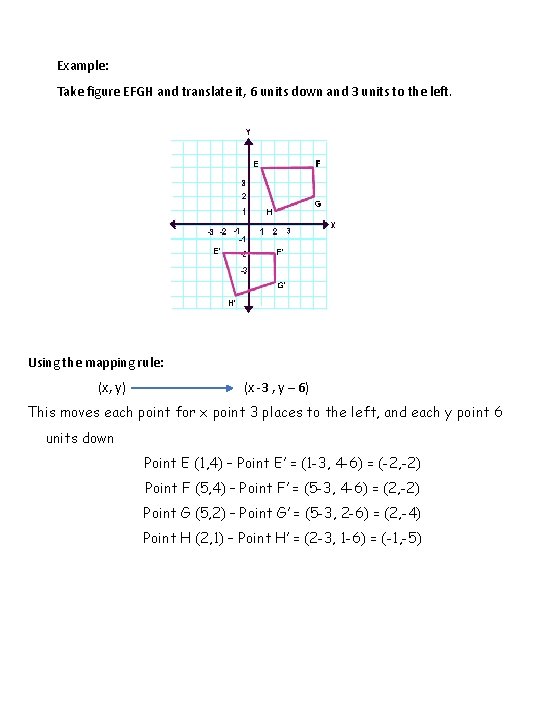
Example: Take figure EFGH and translate it, 6 units down and 3 units to the left. Using the mapping rule: (x, y) (x -3 , y – 6) This moves each point for x point 3 places to the left, and each y point 6 units down Point E (1, 4) – Point E’ = (1 -3, 4 -6) = (-2, -2) Point F (5, 4) – Point F’ = (5 -3, 4 -6) = (2, -2) Point G (5, 2) – Point G’ = (5 -3, 2 -6) = (2, -4) Point H (2, 1) – Point H’ = (2 -3, 1 -6) = (-1, -5)

Example: Kara is a cartographer who makes maps of lakes in her province. She made a mistake on one of her maps and put Bear Lake in the wrong location. She needs to move it 7 km west and 3 km south. Given a Graph you should be able to identify how the final image was created using a translation. The arrow in each graph represents moving to the new position, the arrow points towards the new location of the point.

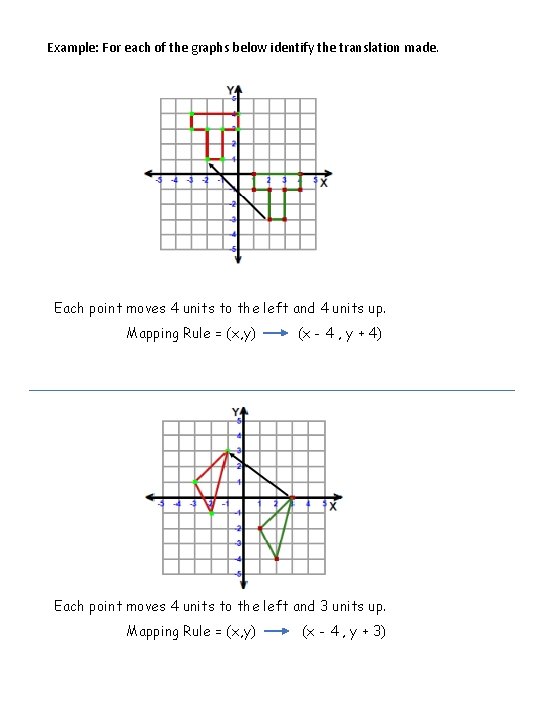
Example: For each of the graphs below identify the translation made. Each point moves 4 units to the left and 4 units up. Mapping Rule = (x, y) (x - 4 , y + 4) Each point moves 4 units to the left and 3 units up. Mapping Rule = (x, y) (x - 4 , y + 3)

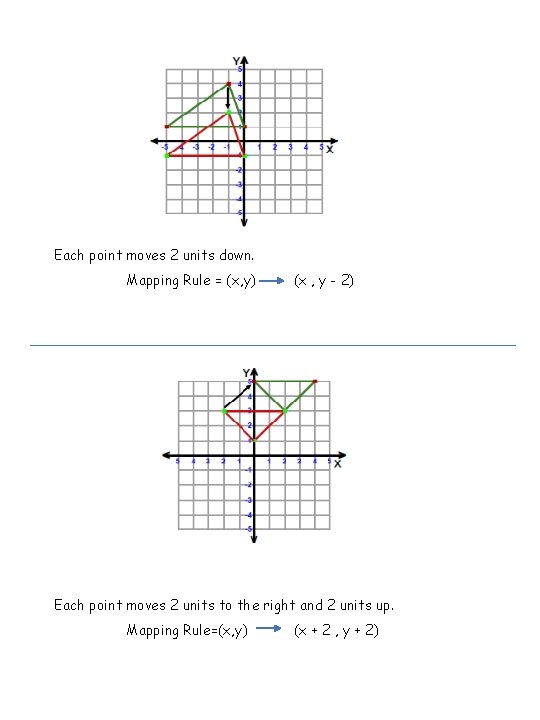
Each point moves 2 units down. Mapping Rule = (x, y) (x , y - 2) Each point moves 2 units to the right and 2 units up. Mapping Rule=(x, y) (x + 2 , y + 2)

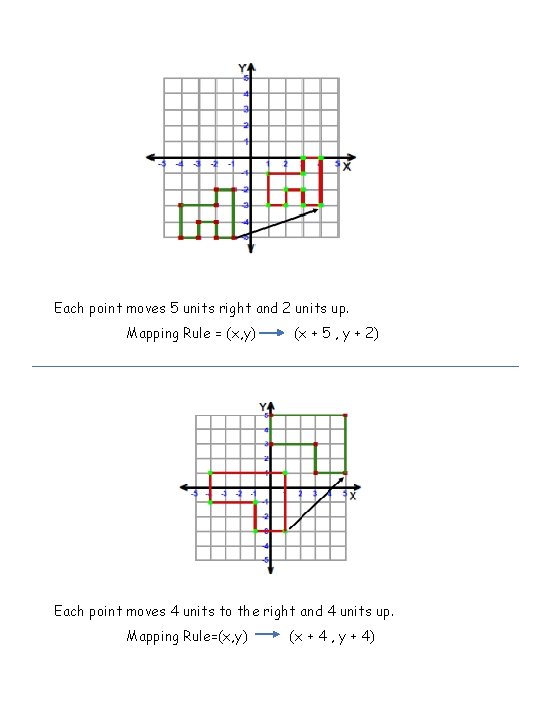
Each point moves 5 units right and 2 units up. Mapping Rule = (x, y) (x + 5 , y + 2) Each point moves 4 units to the right and 4 units up. Mapping Rule=(x, y) (x + 4 , y + 4)

Successive Translations Successive translation is a pattern created by translating a figure multiple times using the same translation. Patterns for quilts, tiles, stone pathways, and many other things are often made by successive translations Example: a) You can make patios from interlocking bricks. Describe the successive translations used to make this patio. Each stone is 2 by 1. To do this we label a single point on our brick pattern. Then we perform translations until we find the right combination to create the pattern that we see. In this case, each stone is translated 1 unit down and 1 unit left.

b) Draw the successive translations on a grid. Plot point A at the origin. Repeat the pattern three times. Draw the pattern, and label point A. Translate A 1 unit down and 1 unit left to (-1, -1). Draw the stone. Do the same for the blue stone. Repeat the pattern two more times.