Translations Shifting Reflecting and Stretching Graphs GPS Algebra

Translations: Shifting, Reflecting and Stretching Graphs GPS Algebra (MM 1 A 1 c) Graph transformations of parent functions

GPS Algebra Standards • MM 1 A 1: c. Graph transformations of basic functions including vertical shifts, stretches, and shrinks, as well as reflections across the x- and y-axes

Objectives • Students will be able to graph transformations of the six parent functions.

Essential Question • How do transformations affect the graphs of functions?

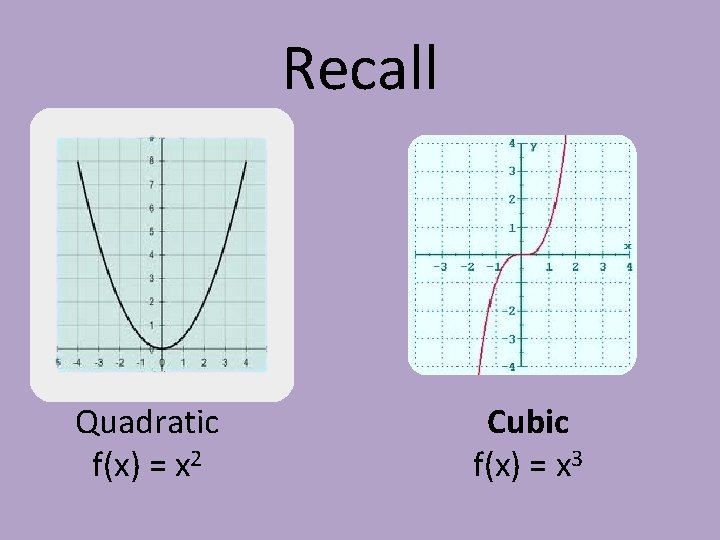
Recall Quadratic f(x) = x 2 Cubic f(x) = x 3

Transformations y = a(x-h)n + k a represents a vertical stretch h represents a horizontal shift; (left, right) k represents a vertical shift; (up, down) n represents the shape of the function (ex. n=3 is cubic) http: //www. wsd 1. org/waec/math/pre-calculus%20 advanced/quadratic%20 functions/transformations/transintro. htm

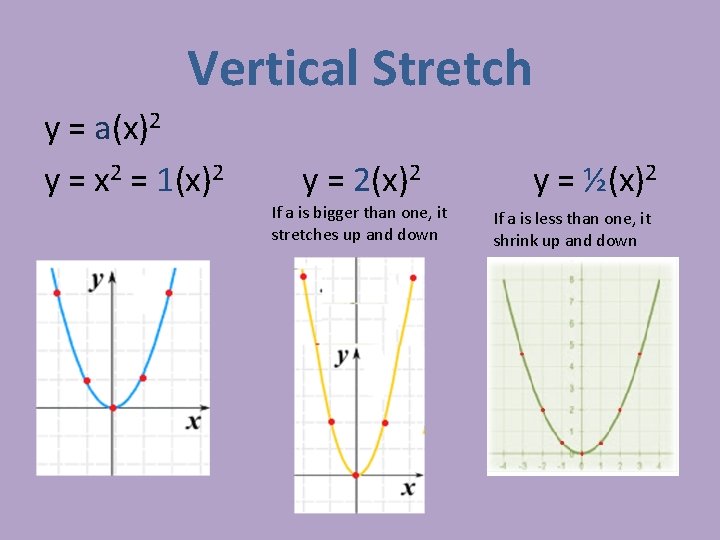
Vertical Stretch y = a(x)2 y = x 2 = 1(x)2 y = 2(x)2 If a is bigger than one, it stretches up and down y = ½(x)2 If a is less than one, it shrink up and down

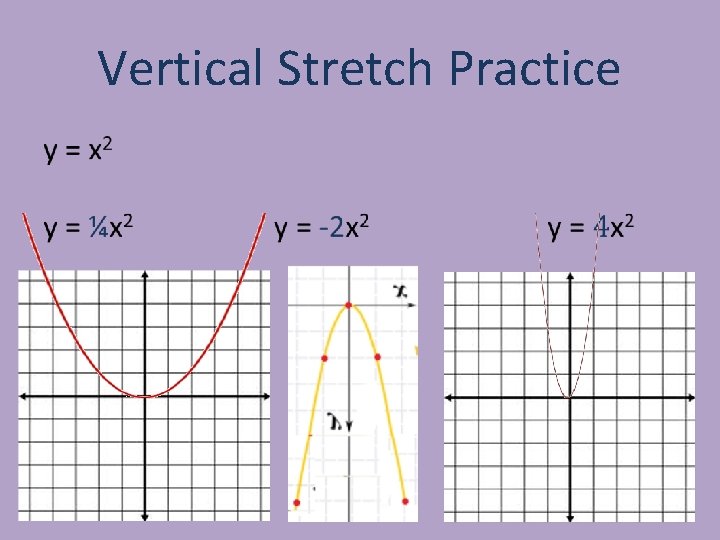
Vertical Stretch Practice •

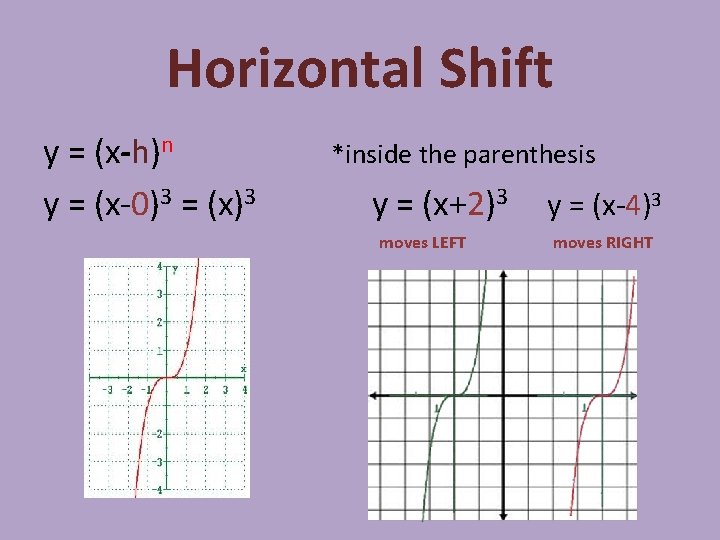
Horizontal Shift y = (x-h)n y = (x-0)3 = (x)3 *inside the parenthesis y = (x+2)3 moves LEFT y = (x-4)3 moves RIGHT

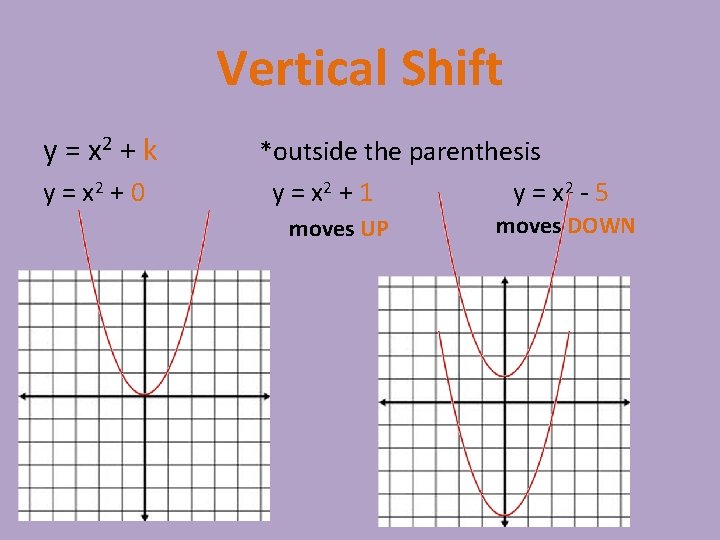
Vertical Shift y = x 2 + k y = x 2 + 0 *outside the parenthesis y = x 2 + 1 y = x 2 - 5 moves UP moves DOWN

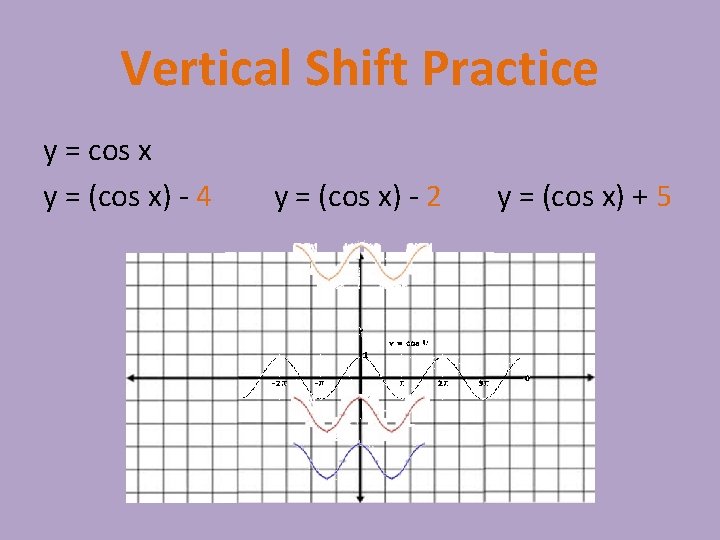
Vertical Shift Practice y = cos x y = (cos x) - 4 y = (cos x) - 2 y = (cos x) + 5

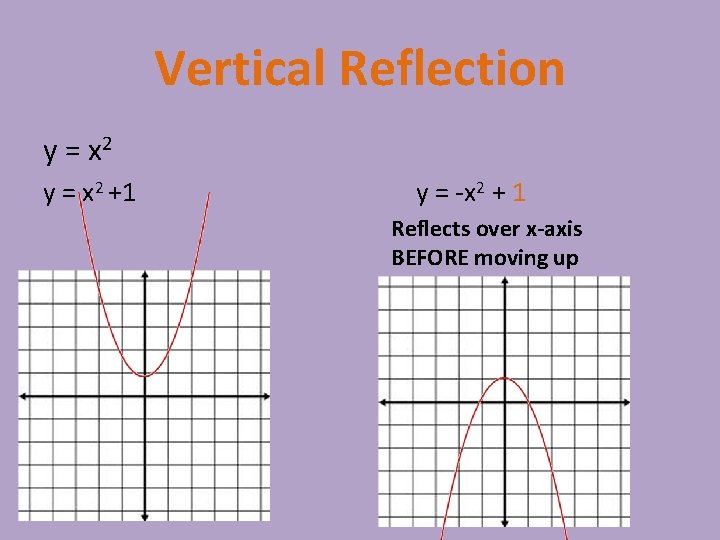
Vertical Reflection y = x 2 +1 y = -x 2 + 1 Reflects over x-axis BEFORE moving up

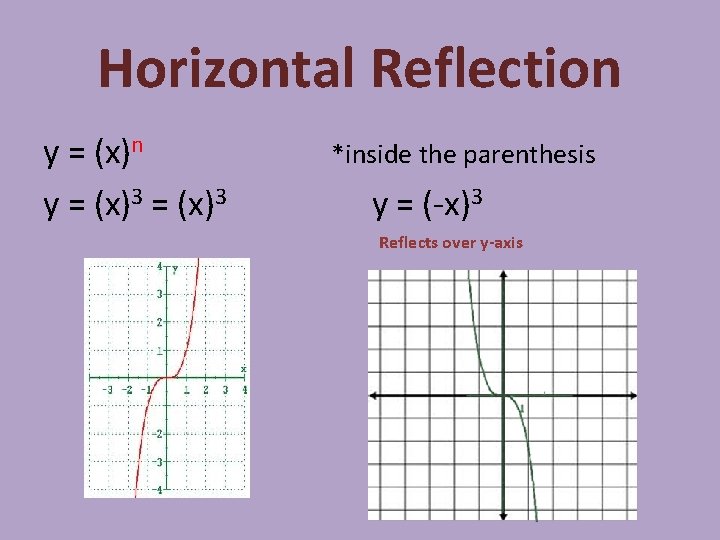
Horizontal Reflection y = (x)3 *inside the parenthesis y = (-x)3 Reflects over y-axis

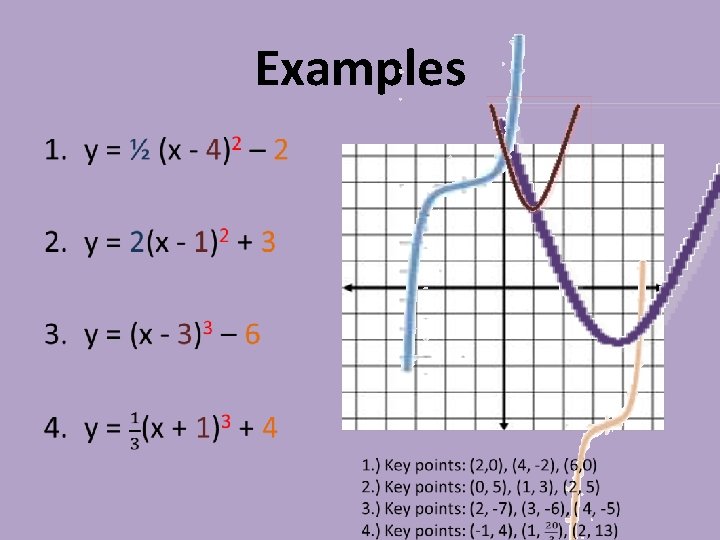
Examples •

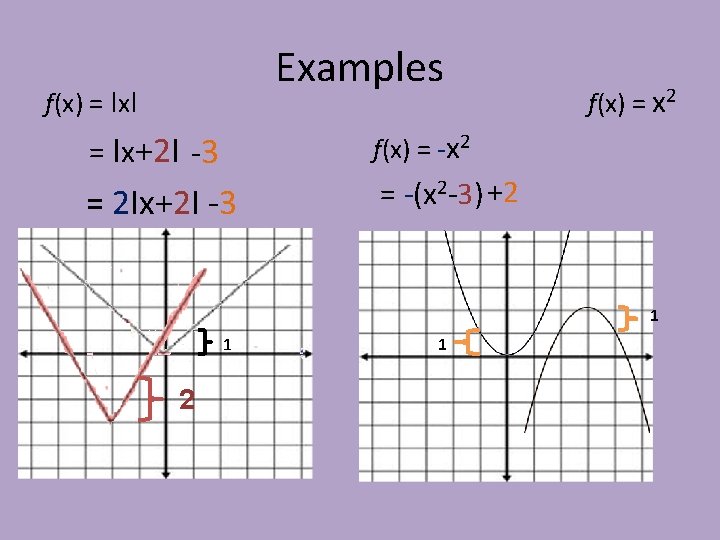
Examples f(x) = Ix. I f(x) = x 2 f(x) = -x 2 = Ix+2 I -3 = 2 Ix+2 I -3 = -(x 2 -3) +2 1 1 2 1

Things to Remember •

Any Questions Translation Symmetry Vertical Line Test Domain & Range

Next class • Factoring Quadratics