Translating from LTL to automata 1 Why translating

Translating from LTL to automata 1

Why translating? n n n Want to write the specification in some logic. Want to check that an automaton (or a Kripke structure) satisfies this property. The check (“model-checking”) will be based on automata operations – hence we need to translate the property to automata. 2

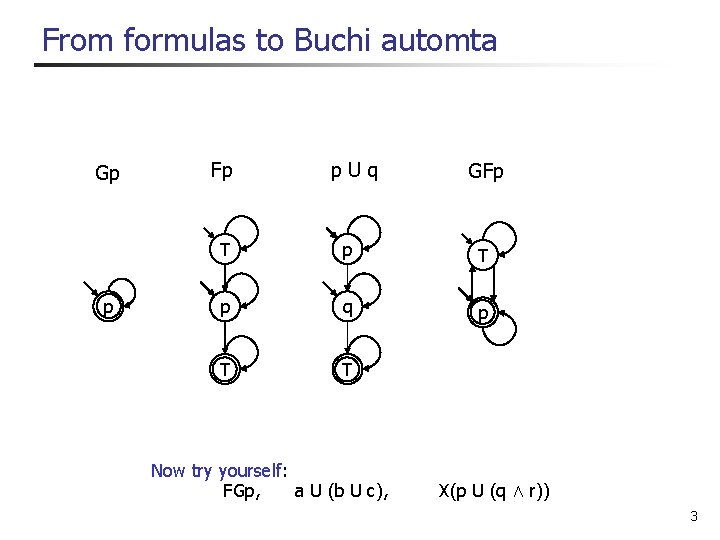
From formulas to Buchi automta Gp p Fp p. Uq GFp T p q p T T Now try yourself: FGp, a U (b U c), X(p U (q Æ r)) 3

A translation algorithm n n So now we need to show an algorithmic translation from LTL to Buchi It will work in two stages: n n Translate to Generalized Buchi Degeneralization. 4

Preprocessing n n n Convert into normal form, where negation only applies to propositional variables. ¬G becomes F¬. ¬F becomes G¬. ¬( U ) becomes (¬ ) R (¬ ), ¬( R ) becomes (¬ ) U (¬ ). 5

Preprocessing n Convert to Negation Normal Form n n Push negations over propositional conenctives, and eliminate operators other than Æ, Ç Eliminate G n Replace G by (False R ). n (in general we can stay with U, R, X) 6

Example n Translate (GF P ) ! ( GF Q ) n n n Eliminate implication ¬( GF P ) Ç ( GF Q ) Eliminate G, F : ¬( False R ( True U P ) ) Ç ( False R ( True U Q ) ) Push negation inwards: (True U (False R ¬P ) ) Ç ( False R ( True U Q ) ) 7

And now. . . n We need to build an automaton that accepts exactly those words that satisfy . 8

Content The construction continues as follows: n 1. 2. 3. Build the Local Automaton n This automaton guarantees that the word satisfies all conditions imposed by the formula Build the Eventuality Automaton n Eventualities : formulas of the form Fφ and φ1 U φ2 n The problem is that nothing prevents us from postponing forever the time at which (eventuality) formula will be true Compose them 9

The Local Automaton n n Closure of : all the subformulas of and their negations. Formally: cl( ) is the smallest set of formulas satisfying the following conditions n n n n φ ∈ cl(φ) φ1 ∈ cl(φ) ⇒ φ1 ∧ φ2∈ cl(φ) φ1 ∨ φ2 ∈ cl(φ) ¬φ1 ∈ cl(φ) ⇒ φ1 , φ2 ∈ cl(φ) X φ1 ∈ cl(φ) ⇒ F φ1 ∈ cl(φ) ⇒ φ1 U φ2 ∈ cl(φ) φ1 R φ2 ∈ cl(φ) φ1 ∈ cl(φ) ⇒ φ1 , φ2 ∈ cl(φ) 10

The Local Automaton / Alphabet, states n The local automaton is L = (∑, SL, ρL, IL, FL) n The alphabet ∑ n n n ∑ µ 2 cl(φ) ∑ elements are consistent: for s 2 ∑ and f ∈ cl(φ): f ∈ s ¬f ∉ s The states SL n All propositionally consistent subsets s of cl(φ): n φ1 ∈ s ¬φ1 ∉ s 11

The Local Automaton / Transition relation The edges: n ρL(s, a) must check the next state is compatible with the semantics of the temporal operators. n n Let t ∈ ρL(s, a). Then: Xφ1 ∈ s φ1 ∈ t n Fφ1 ∈ s or Fφ1 ∈ t n φ1 U φ2 ∈ s (φ2 ∈ s) or (φ1 ∈ s and φ1 U φ2 ∈ t) n φ1 R φ2 ∈ s (φ1 ⋀ φ2 ∈ s) or (φ2 ∈ s and φ1 R φ2 ∈ t) The labeling on the edges: n For a state s ; , s is the label on all the outgoing edges from s. 12

The Local Automaton / Initial + final states n The initial states IL n n . . . is the set of states that include the formula The accepting states FL n . . . is the set of all states 13

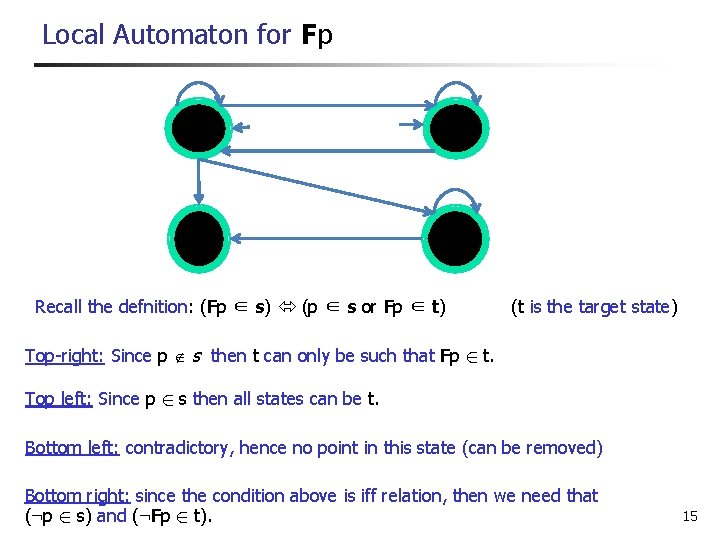
Example: Local Automaton for Fp n Closure of Fp n n cl(Fp) = {Fp, p, ¬Fp, ¬p} SL= {{Fp, p}, {¬Fp, p}, {Fp, ¬p}, {¬Fp, ¬p}} 14

Local Automaton for Fp {Fp, p} {Fp, ¬p} {¬Fp, ¬p} Recall the defnition: (Fp ∈ s) (p ∈ s or Fp ∈ t) (t is the target state) Top-right: Since p s then t can only be such that Fp 2 t. Top left: Since p 2 s then all states can be t. Bottom left: contradictory, hence no point in this state (can be removed) Bottom right: since the condition above is iff relation, then we need that (: p 2 s) and (: Fp 2 t). 15

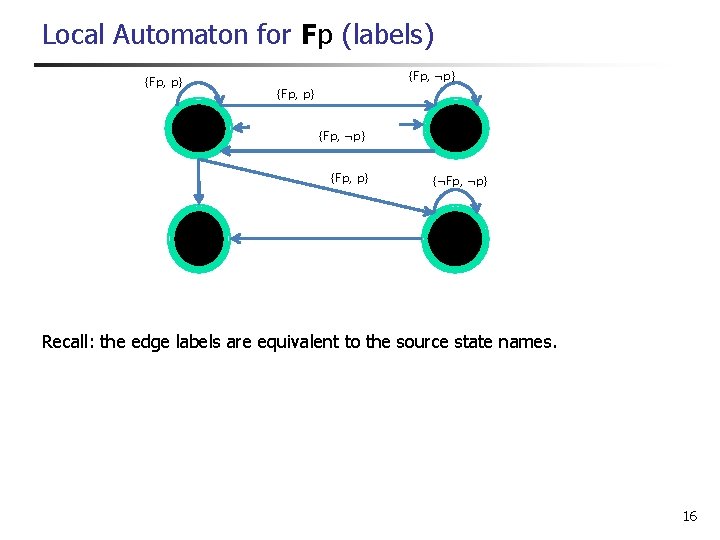
Local Automaton for Fp (labels) {Fp, p} {Fp, ¬p} {Fp, p} {¬Fp, p} {Fp, ¬p} {¬Fp, ¬p} Recall: the edge labels are equivalent to the source state names. 16

The Eventuality Automaton n Eventuality automaton is supposed to check that the eventualities are realized n Check formulas of the form n φ1 U φ2 n Fφ // special case of U 17

The Eventuality Automaton/ Alphabet, states n Ev = (∑, 2 ev(φ), ρF, {{}}, F) n The alphabet n n n ∑ µ 2 cl(φ) ∑ elements are consistent: for s 2 ∑ and f ∈ cl(φ): f ∈ s ¬f ∉ s The states 2 ev(φ) n n The set of subsets of the eventualities of the formula φ A state {e 1, …, ek} means that the eventualities e 1, …, ek still have to be realized 18

The Eventuality Automaton/ Transition relation, initial state n The transition ρF n n Let t ∈ ρF(s, a) n For Fφ : Fφ ∈ t φ ∉ a n For φ1 U φ2 : φ1 U φ2 ∈ t φ2 ∉ a The initial state : {} 19

The Eventuality Automaton/ accepting states n The acceptance condition F is complicated. . . n When can we accept a state s? n n if s has an eventuality, it satisfies it. Examples: n s is accepting: s = {p. Uq, : p, q} s = {: p. Uq, : p, : q} n s is not accepting: s = {p. Uq, p, : q} s = {p. Uq, : p, : q} 20

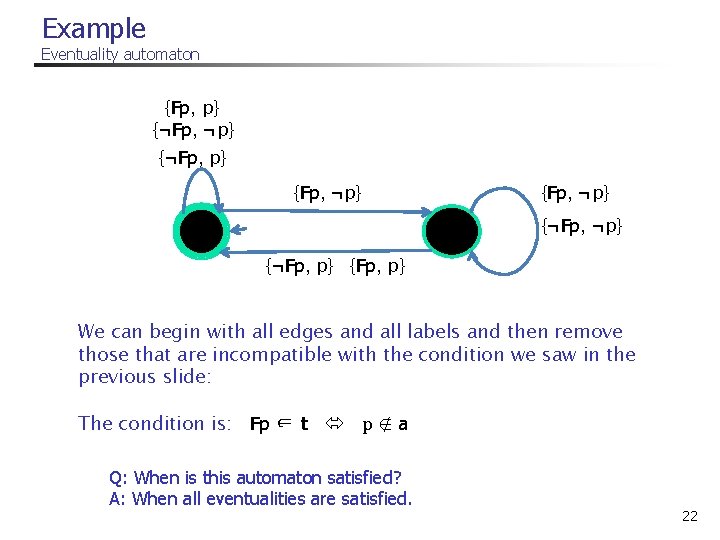
The Eventuality Automaton/ accepting states n The acceptance condition, formaly: n n n Let ei be an eventuality condition i’ U i Suppose we have the eventuality conditions e 1, . . . , em. Then F is a generalized Buchi condition: F = {Á1, . . . , Ám} where Ái = {s 2 S | ei 2 s ! i 2 s} n In our example: n n We have two states: {} and {Fp} Thus, F contains the single state {} 21

Example Eventuality automaton {Fp, p} {¬Fp, ¬p} {¬Fp, p} {Fp, ¬p} {Fp} {} {¬Fp, ¬p} {¬Fp, p} {Fp, p} We can begin with all edges and all labels and then remove those that are incompatible with the condition we saw in the previous slide: The condition is: Fp ∈ t p ∉ a Q: When is this automaton satisfied? A: When all eventualities are satisfied. 22

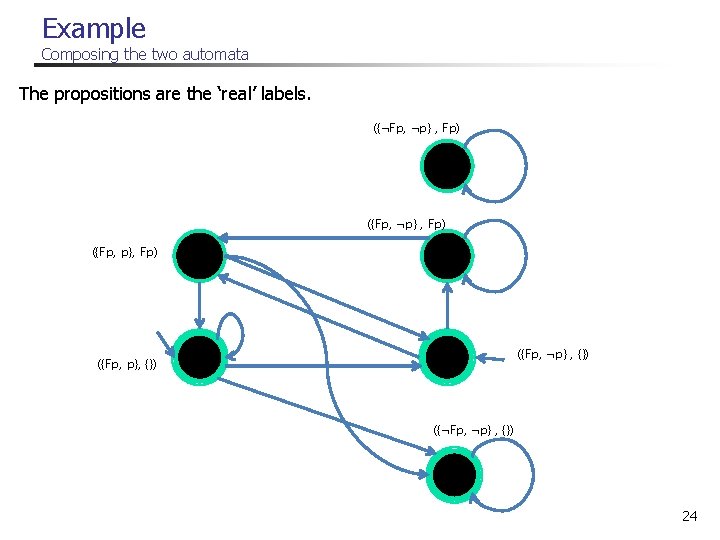
Composing the two automata n M = (∑, SM, ρM , NM 0, FM) n ∑ µ 2 cl( ) n SM = SL x 2 ev(φ) n (p, q) ∈ ρM((s, t), a) p ∈ ρL(s, a) and q ∈ ρF(t, a) n NM 0 = Nφ x {} n FM = NL x {} (Cartesian Product) 23

Example Composing the two automata The propositions are the ‘real’ labels. ({¬Fp, ¬p} , Fp) ({Fp, p}, Fp) p : p ({Fp, p}, {}) p : p ({Fp, ¬p} , {}) ({¬Fp, ¬p} , {}) : p 24

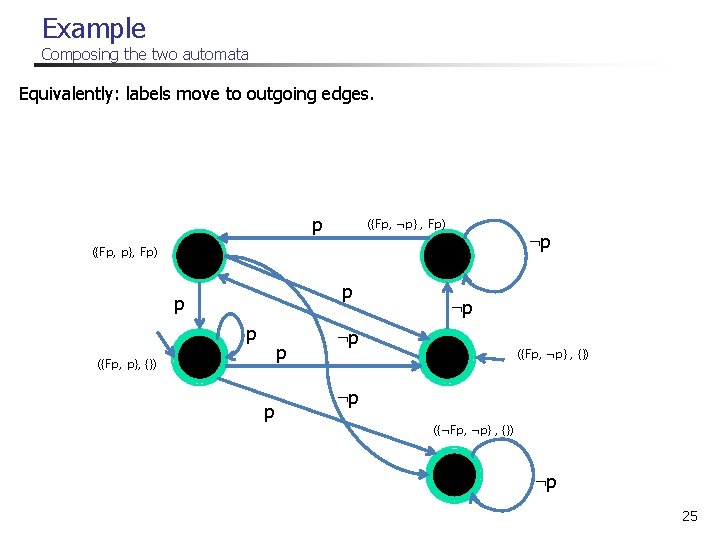
Example Composing the two automata Equivalently: labels move to outgoing edges. p ({Fp, ¬p} , Fp) : p ({Fp, p}, Fp) p p ({Fp, p}, {}) p : p ({Fp, ¬p} , {}) : p ({¬Fp, ¬p} , {}) : p 25

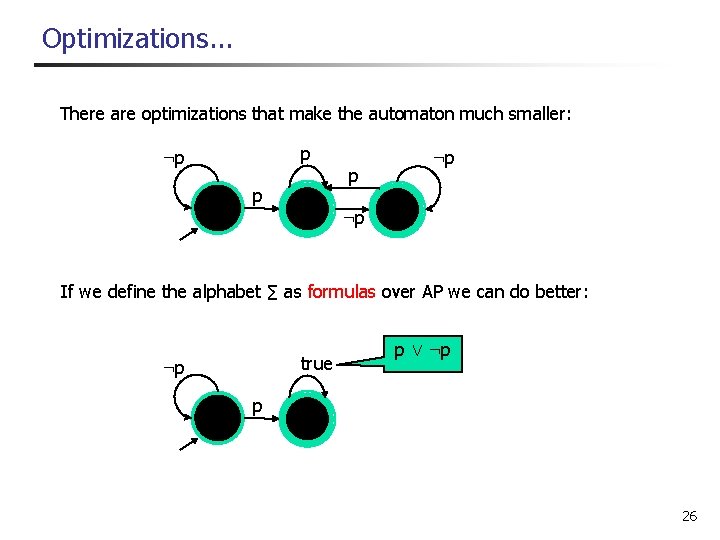
Optimizations. . . There are optimizations that make the automaton much smaller: p p p : p If we define the alphabet ∑ as formulas over AP we can do better: true : p p Ç : p p 26

Conclusion n The number of States n Local Automaton : 2 cl(φ) = O(22|φ|) Eventuality Automaton : 2 ev(φ) = O(2|φ|) Composed Automata : 2 cl(φ) X 2 ev(φ) = O(23|φ|) n |φ| is length of formula φ n n 27