Transition from Pervasive to Segregated Fluid Flow in

Transition from Pervasive to Segregated Fluid Flow in Ductile Rocks James Connolly and Yuri Podladchikov, ETH Zurich A transition between “Darcy” and Stokes regimes • • Geological scenario Review of steady flow instabilities => porosity waves • Analysis of conditions for disaggregation

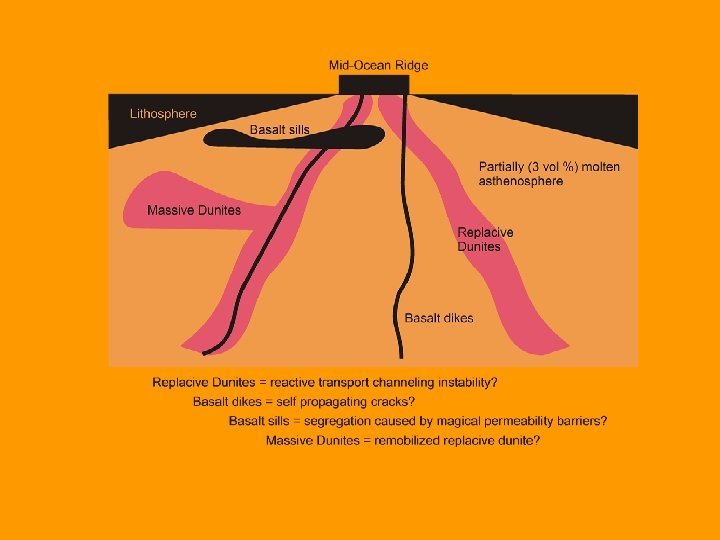
lithosphere

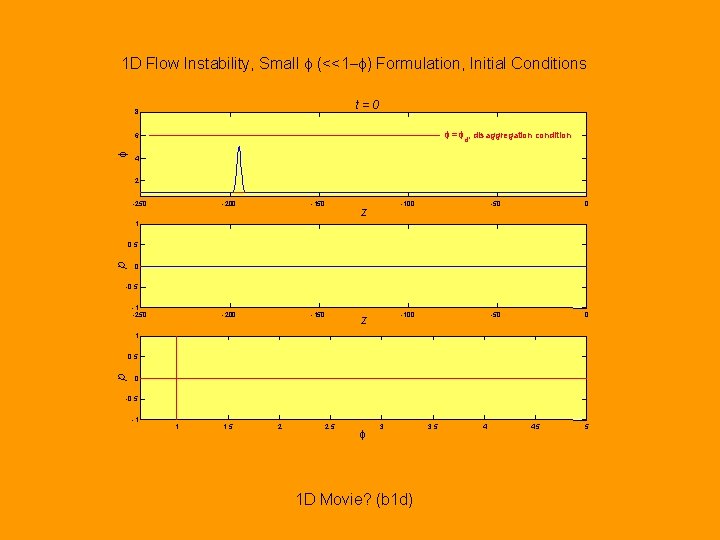
1 D Flow Instability, Small f (<<1 -f) Formulation, Initial Conditions t=0 8 f = f , disaggregation condition d f 6 4 2 -250 -200 -150 z -100 -50 0 1 p 0. 5 0 -0. 5 -1 -250 z 1 p 0. 5 0 -0. 5 -1 1 1. 5 2 2. 5 f 3 1 D Movie? (b 1 d) 3. 5 4 4. 5 5

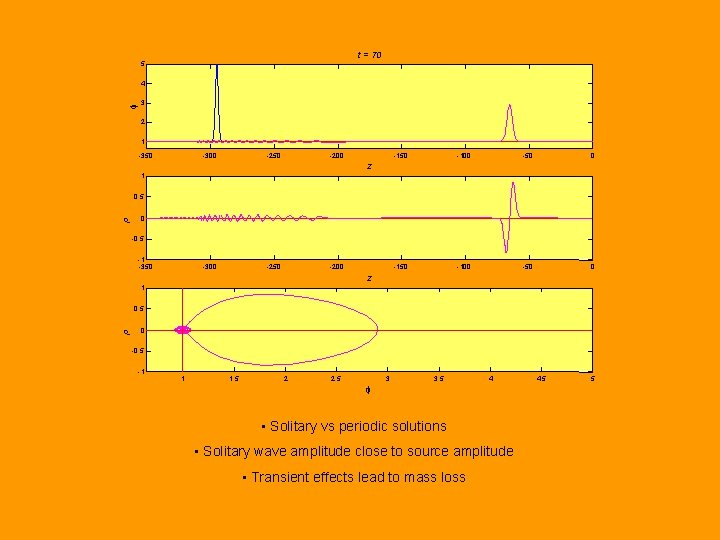
t = 70 5 4 f 1 D Final 3 2 1 -350 -300 -250 -200 -150 -100 -50 0 z 1 p 0. 5 0 -0. 5 -1 -350 -300 -250 -200 z 1 p 0. 5 0 -0. 5 -1 1 1. 5 2 2. 5 3 3. 5 4 f • Solitary vs periodic solutions • Solitary wave amplitude close to source amplitude • Transient effects lead to mass loss 4. 5 5

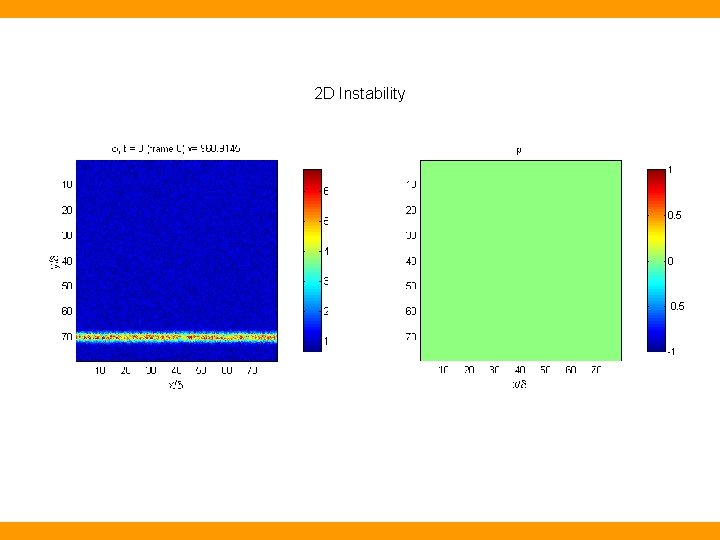
2 D Instability

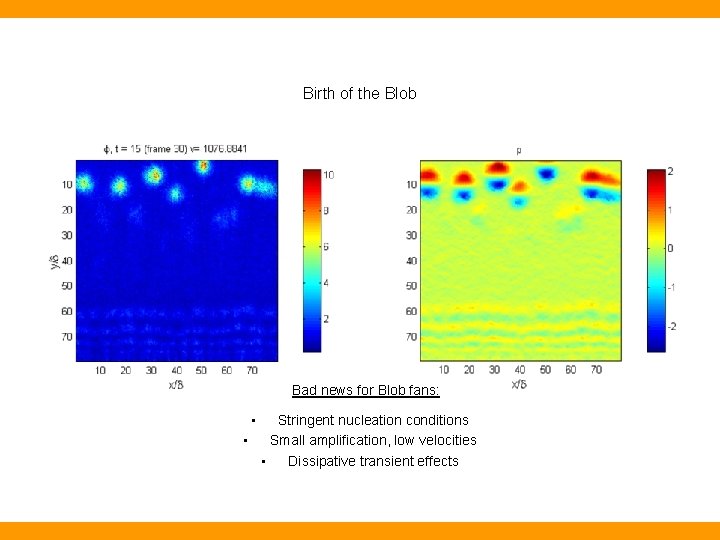
Birth of the Blob Bad news for Blob fans: • Stringent nucleation conditions • Small amplification, low velocities • Dissipative transient effects

Is the blob model stupid? A differential compaction model Dike Movie? (z 2 d)

The details of dike-like waves Comparison movie (y 2 d 2)

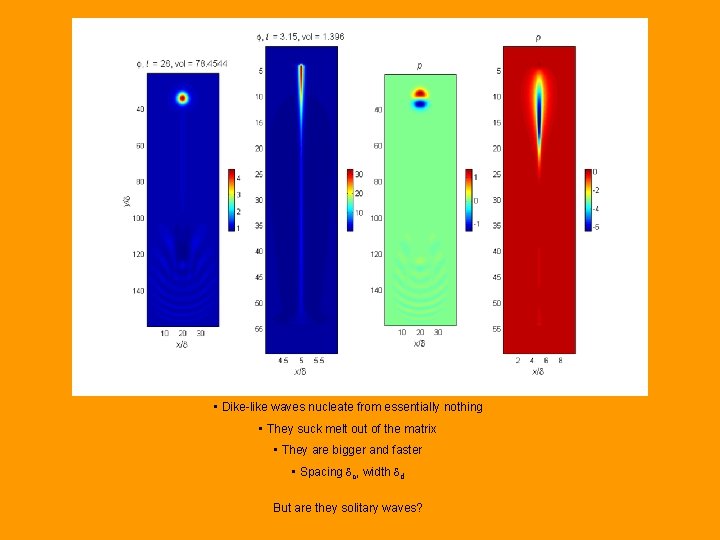
Final comparison • Dike-like waves nucleate from essentially nothing • They suck melt out of the matrix • They are bigger and faster • Spacing dc, width dd But are they solitary waves?

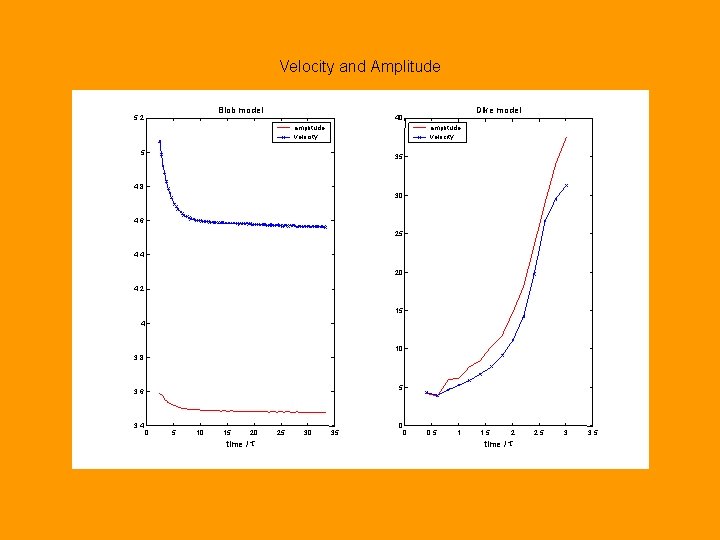
Velocity and Amplitude Blob model 5. 2 Dike model 40 amplitude velocity 5 35 4. 8 30 4. 6 25 4. 4 20 4. 2 15 4 10 3. 8 5 3. 6 3. 4 0 5 10 15 20 time / t 25 30 35 0 0 0. 5 1 1. 5 2 time / t 2. 5 3 3. 5

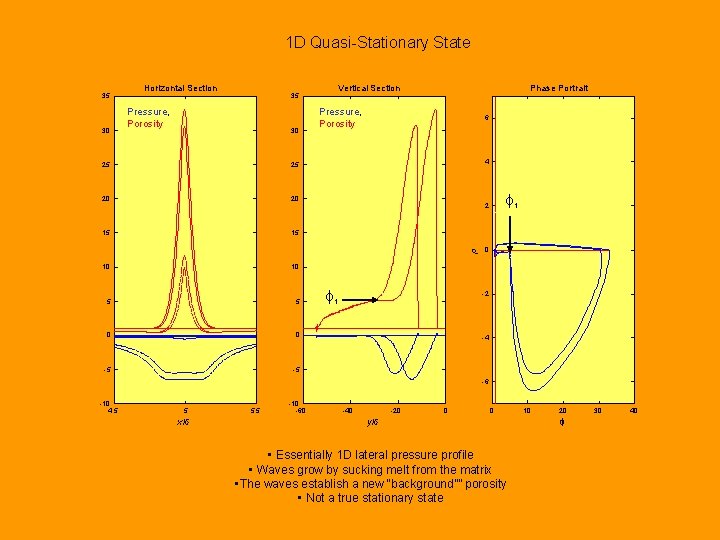
1 D Quasi-Stationary State 35 30 Horizontal Section 35 Pressure, Porosity 30 25 20 20 15 15 Phase Portrait Pressure, Porosity 6 4 10 10 5 5 0 0 -5 -5 f 1 2 p 25 Vertical Section f 1 0 -2 -4 -6 -10 4. 5 5 x/d 5. 5 -10 -60 -40 -20 0 0 y/d • Essentially 1 D lateral pressure profile • Waves grow by sucking melt from the matrix • The waves establish a new “background”” porosity • Not a true stationary state 10 20 f 30 40

So dike-like waves are the ultimate in porosity-wave fashion: They nucleate out of essentially nothing They suck melt out of the matrix They seem to grow inexorably toward disaggregation But Do they really grow inexorably, what about 1 -f? Can we predict the conditions (fluxes) for disaggregation? Simple 1 D analysis

Mathematical Formulation • Incompressible viscous fluid and solid components • Darcy’s law with k = f(f), Eirik’s talk • Viscous bulk rheology with (geological formulations ala Mc. Kenzie have • 1 D stationary states traveling with phase velocity w )

Balancing ball

H(omega)

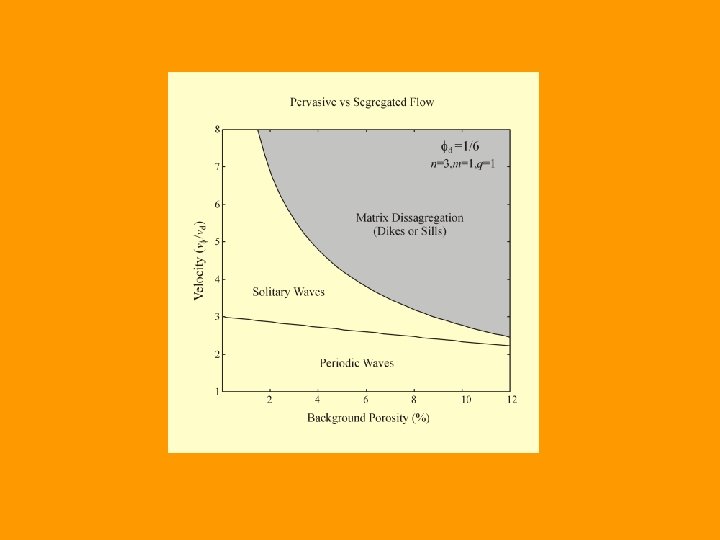
Phase diagram

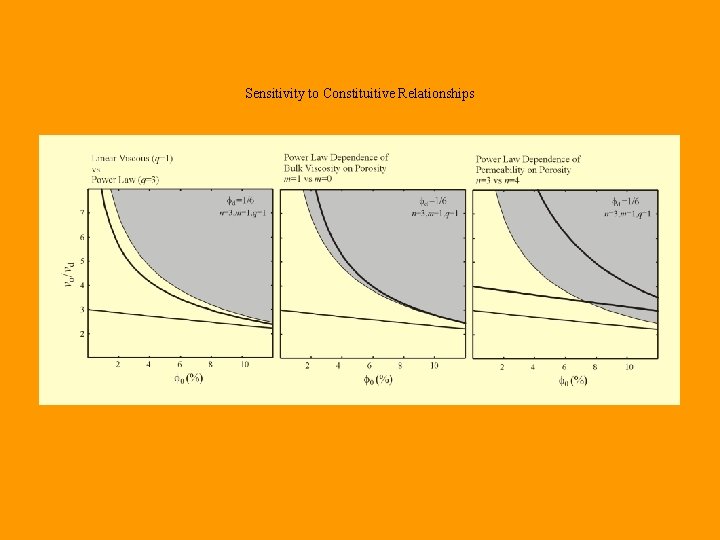
Sensitivity to Constituitive Relationships