Transistor Building Block of Computers Microprocessors contain millions

Transistor: Building Block of Computers Microprocessors contain millions of transistors • Intel Pentium 4 (2000): 48 million • IBM Power. PC 750 FX (2002): 38 million • IBM/Apple Power. PC G 5 (2003): 58 million Logically, each transistor acts as a switch Combined to implement logic functions • AND, OR, NOT Combined to build higher-level structures • Adder, multiplexer, decoder, register, … Combined to build processor • LC-3 3 -1

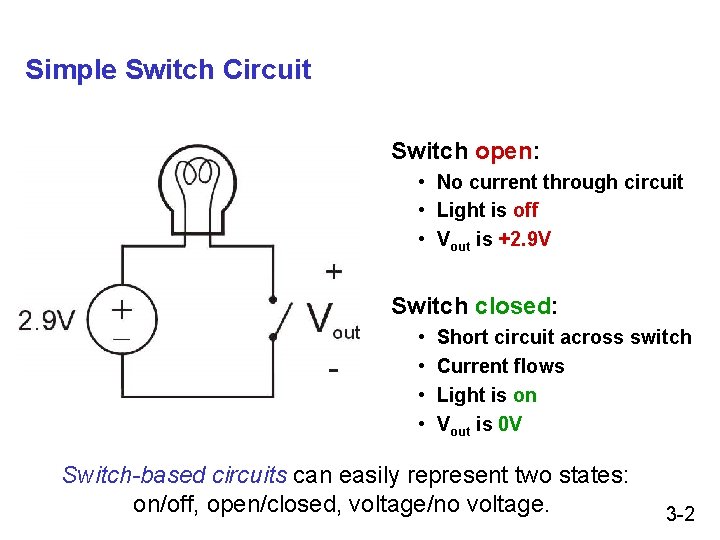
Simple Switch Circuit Switch open: • No current through circuit • Light is off • Vout is +2. 9 V Switch closed: • • Short circuit across switch Current flows Light is on Vout is 0 V Switch-based circuits can easily represent two states: on/off, open/closed, voltage/no voltage. 3 -2

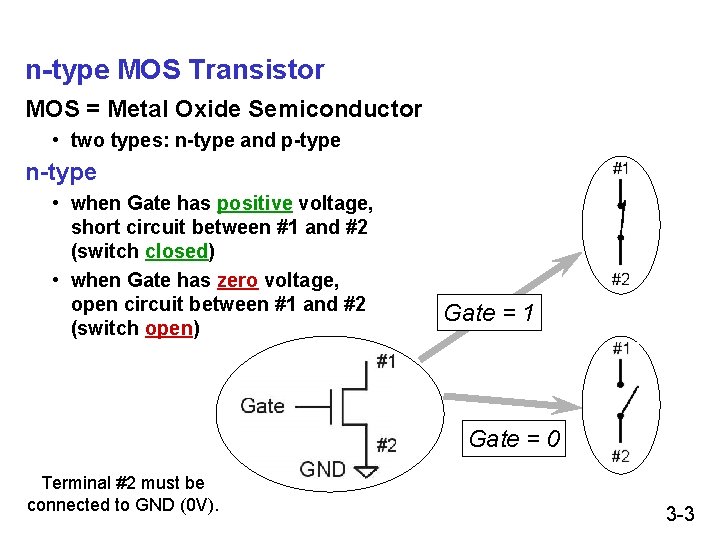
n-type MOS Transistor MOS = Metal Oxide Semiconductor • two types: n-type and p-type n-type • when Gate has positive voltage, short circuit between #1 and #2 (switch closed) • when Gate has zero voltage, open circuit between #1 and #2 (switch open) Gate = 1 Gate = 0 Terminal #2 must be connected to GND (0 V). 3 -3

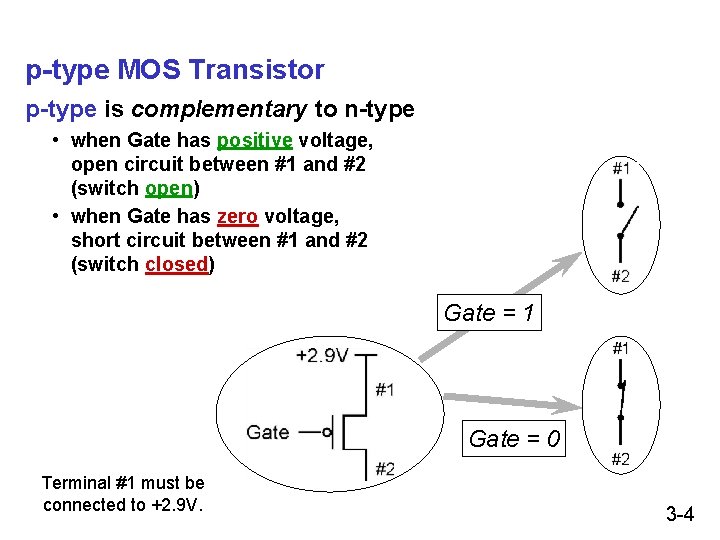
p-type MOS Transistor p-type is complementary to n-type • when Gate has positive voltage, open circuit between #1 and #2 (switch open) • when Gate has zero voltage, short circuit between #1 and #2 (switch closed) Gate = 1 Gate = 0 Terminal #1 must be connected to +2. 9 V. 3 -4

Logic Gates Use switch behavior of MOS transistors to implement logical functions: AND, OR, NOT. Digital symbols: • recall that we assign a range of analog voltages to each digital (logic) symbol • assignment of voltage ranges depends on electrical properties of transistors being used Ø typical values for "1": +5 V, +3. 3 V, +2. 9 V Ø from now on we'll use +2. 9 V 3 -5

CMOS Circuit Complementary MOS Uses both n-type and p-type MOS transistors • p-type Ø Attached to + voltage Ø Pulls output voltage UP when input is zero • n-type Ø Attached to GND Ø Pulls output voltage DOWN when input is one For all inputs, make sure that output is either connected to GND or to +, but not both! 3 -6

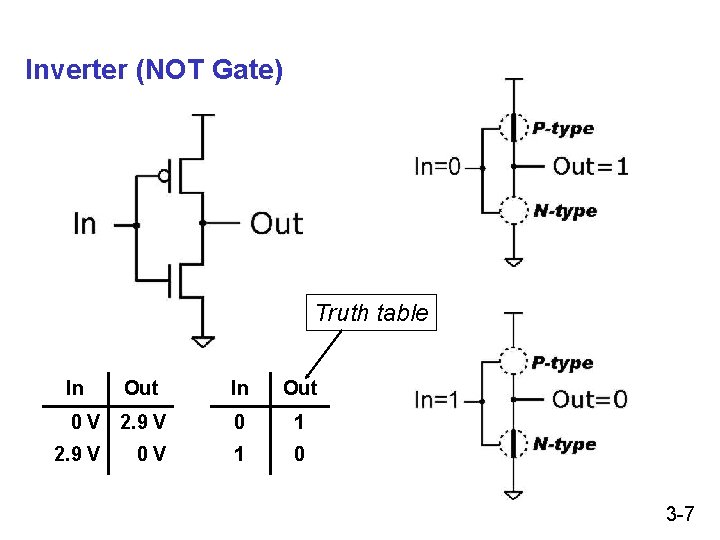
Inverter (NOT Gate) Truth table In Out 0 V 2. 9 V 0 V In Out 0 1 1 0 3 -7

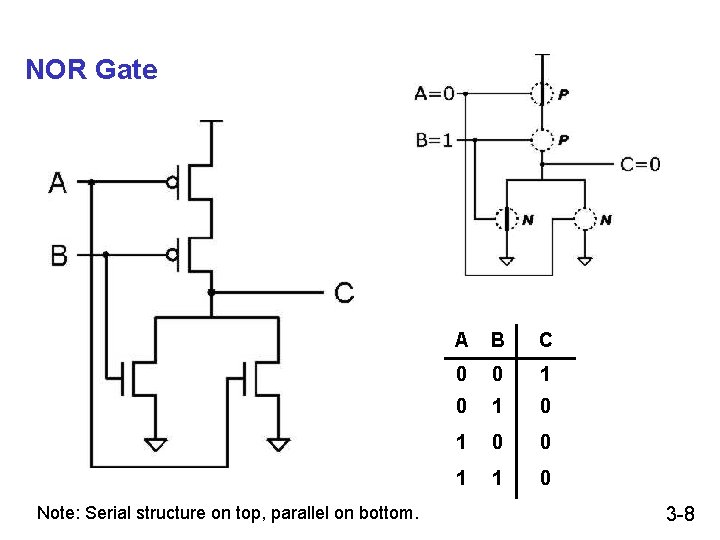
NOR Gate Note: Serial structure on top, parallel on bottom. A B C 0 0 1 0 1 0 0 1 1 0 3 -8

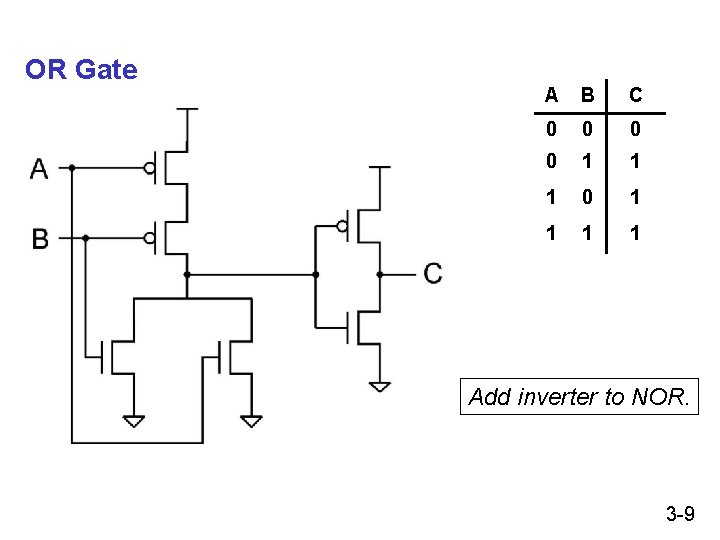
OR Gate A B C 0 0 1 1 1 0 1 1 Add inverter to NOR. 3 -9

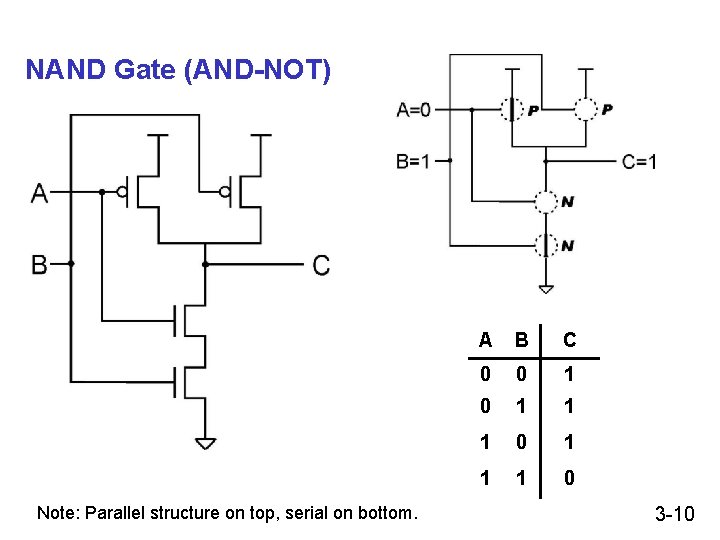
NAND Gate (AND-NOT) Note: Parallel structure on top, serial on bottom. A B C 0 0 1 1 1 0 3 -10

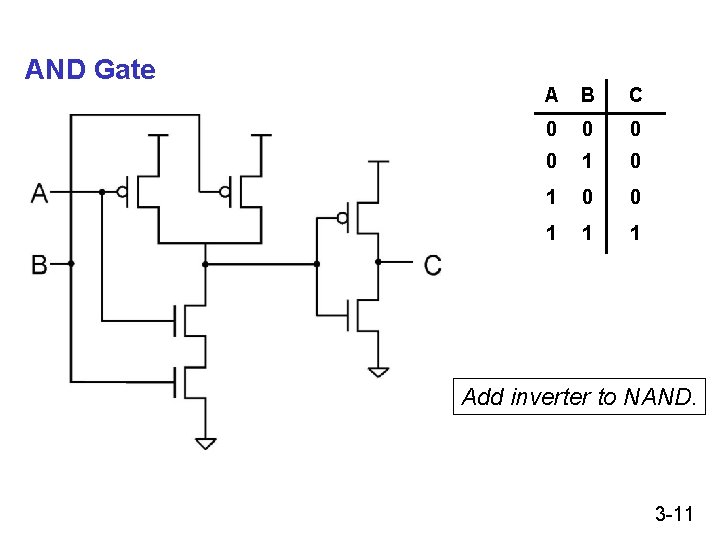
AND Gate A B C 0 0 1 1 1 Add inverter to NAND. 3 -11

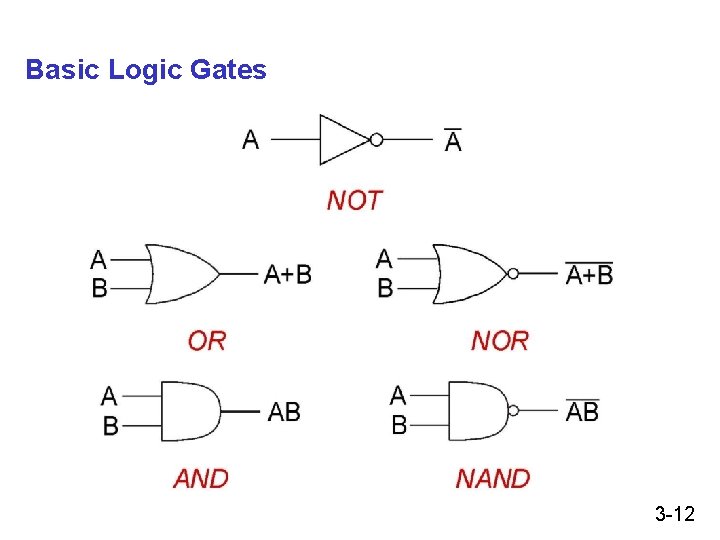
Basic Logic Gates 3 -12

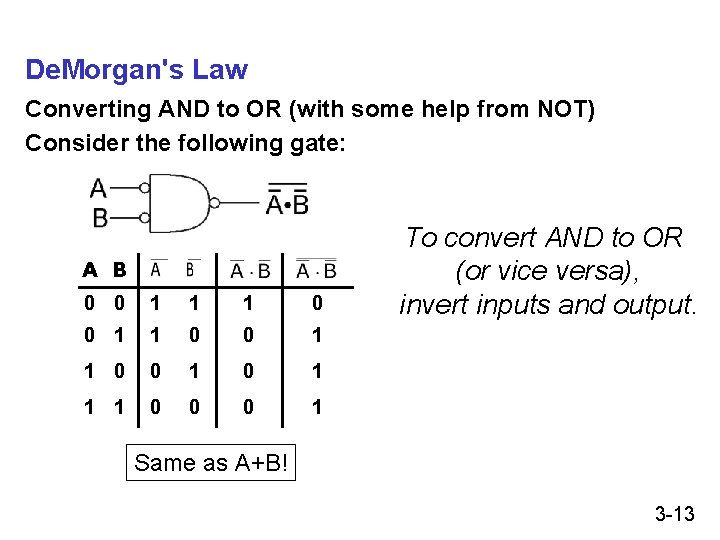
De. Morgan's Law Converting AND to OR (with some help from NOT) Consider the following gate: A B 0 0 1 1 1 0 0 1 1 1 0 0 0 1 To convert AND to OR (or vice versa), invert inputs and output. Same as A+B! 3 -13

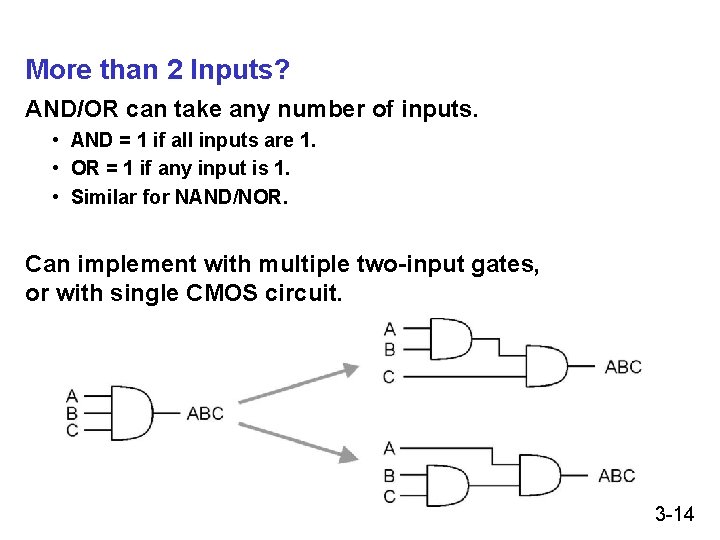
More than 2 Inputs? AND/OR can take any number of inputs. • AND = 1 if all inputs are 1. • OR = 1 if any input is 1. • Similar for NAND/NOR. Can implement with multiple two-input gates, or with single CMOS circuit. 3 -14

Summary MOS transistors are used as switches to implement logic functions. • n-type: connect to GND, turn on (with 1) to pull down to 0 • p-type: connect to +2. 9 V, turn on (with 0) to pull up to 1 Basic gates: NOT, NOR, NAND • Logic functions are usually expressed with AND, OR, and NOT De. Morgan's Law • Convert AND to OR (and vice versa) by inverting inputs and output 3 -15

Building Functions from Logic Gates Combinational Logic Circuit • output depends only on the current inputs • stateless Sequential Logic Circuit • output depends on the sequence of inputs (past and present) • stores information (state) from past inputs We'll first look at some useful combinational circuits, then show to use sequential circuits to store information. 3 -16

Binary Logic Function F(vars) = expression n. Operators set of binary variables n. Variables ( +, • , ‘ ) n. Constants ( 0, 1 ) n. Groupings (parenthesis) Example: F(a, b) = a’ • b + b’ G(x, y, z) = x • (y+z’) 12/29/2021 10: 12 PM Boolean Algebra PJF - 17

Basic Logic Operators • AND • OR • NOT Binary Unary • F(a, b) = a • b, F is 1 if and only if a=b=1 • G(a, b) = a+b, G is 1 if either a=1 or b=1 • H(a) = a’, H is 1 if a=0 12/29/2021 10: 12 PM Boolean Algebra PJF - 18

Basic Logic Operators (cont. ) • 1 -bit logic AND resembles binary multiplication: 0 • 0 = 0, 1 • 0 = 0, 0 • 1 = 0, 1 • 1 =1 • 1 -bit logic OR resembles binary addition, except for one operation: 0 + 0 = 0, 1 + 0 = 1, 12/29/2021 10: 12 PM 0 + 1 = 1, 1 + 1 = 1 (≠ 102) Boolean Algebra PJF - 19

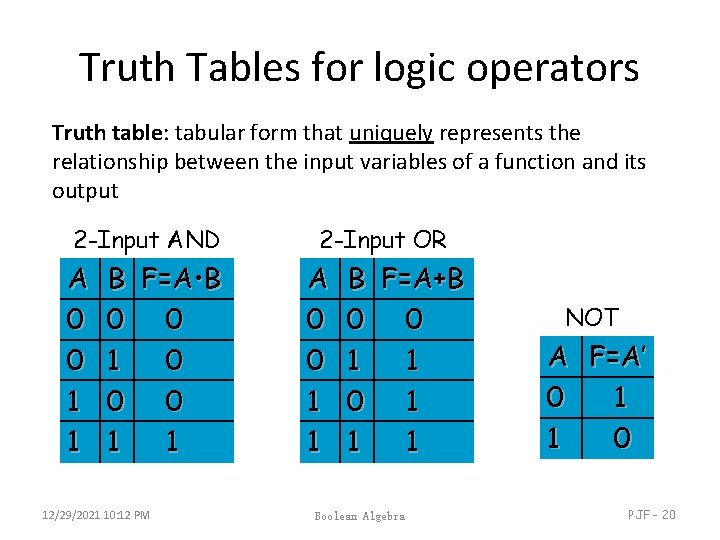
Truth Tables for logic operators Truth table: tabular form that uniquely represents the relationship between the input variables of a function and its output 2 -Input AND A 0 0 1 1 B F=A • B 0 0 1 0 0 0 1 1 12/29/2021 10: 12 PM 2 -Input OR A 0 0 1 1 B F=A+B 0 0 1 1 1 Boolean Algebra NOT A F=A’ 0 1 1 0 PJF - 20

Truth Tables (cont. ) • Q: Let a function F() depend on n variables. How many rows are there in the truth table of F() ? n n n A: 2 rows, since there are 2 possible binary patterns/combinations for the n variables 12/29/2021 10: 12 PM Boolean Algebra PJF - 21

Logic Gates • Logic gates are abstractions of electronic circuit components that operate on one or more input signals to produce an output signal. 2 -Input AND A B F F = A • B 12/29/2021 10: 12 PM 2 -Input OR A B G G = A+B Boolean Algebra NOT (Inverter) A H H = A’ PJF - 22

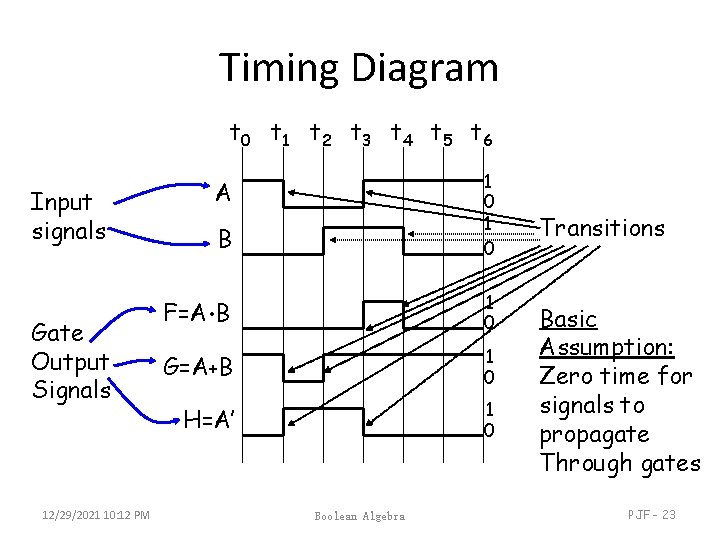
Timing Diagram t 0 t 1 t 2 t 3 t 4 t 5 t 6 Input signals Gate Output Signals 12/29/2021 10: 12 PM B 1 0 F=A • B 1 0 G=A+B 1 0 H=A’ 1 0 A Boolean Algebra Transitions Basic Assumption: Zero time for signals to propagate Through gates PJF - 23

Combinational Logic Circuit from Logic Function • Consider function F = A’ + B • C’ + A’ • B’ • A combinational logic circuit can be constructed to implement F, by appropriately connecting input signals and logic gates: – Circuit input signals from function variables (A, B, C) – Circuit output signal function output (F) – Logic gates from logic operations C F A B 12/29/2021 10: 12 PM Boolean Algebra PJF - 24

Combinational Logic Circuit from Logic Function (cont. ) • In order to design a cost-effective and efficient circuit, we must minimize the circuit’s size (area) and propagation delay (time required for an input signal change to be observed at the output line) • Observe the truth table of F=A’ + B • C’ + A’ • B’ and G=A’ + B • C’ • Truth tables for F and G are identical same function • Use G to implement the logic circuit (less components) 12/29/2021 10: 13 PM Boolean Algebra A B C F G 0 0 0 1 1 1 0 1 1 1 0 0 1 1 1 1 1 0 0 PJF - 25

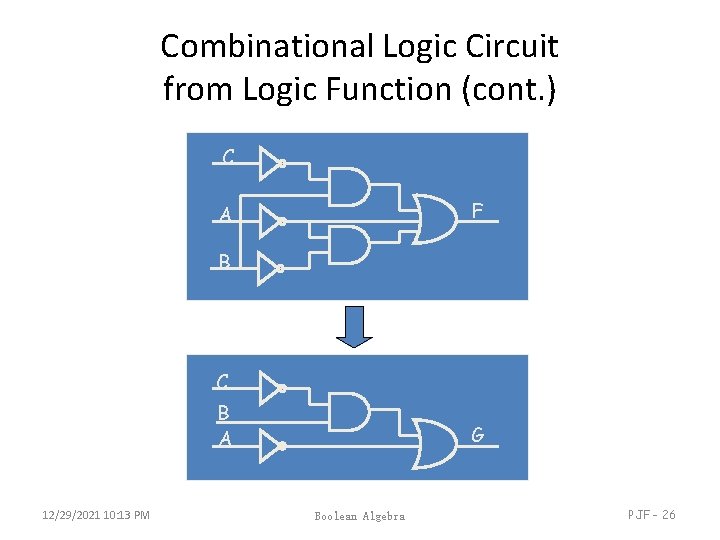
Combinational Logic Circuit from Logic Function (cont. ) C F A B C B A 12/29/2021 10: 13 PM G Boolean Algebra PJF - 26

Boolean Algebra • VERY nice machinery used to manipulate (simplify) Boolean functions • George Boole (1815 -1864): “An investigation of the laws of thought” • Terminology: – Literal: A variable or its complement – Product term: literals connected by • – Sum term: literals connected by + 12/29/2021 10: 13 PM Boolean Algebra PJF - 27

Boolean Algebra Properties Let X: boolean variable, 0, 1: constants 1. 2. 3. 4. X + 0 = X -- Zero Axiom X • 1 = X -- Unit Axiom X + 1 = 1 -- Unit Property X • 0 = 0 -- Zero Property 12/29/2021 10: 13 PM Boolean Algebra PJF - 28

Boolean Algebra Properties (cont. ) Let X: boolean variable, 0, 1: constants 5. 6. 7. 8. 9. X + X = X -- Idepotence X • X = X -- Idepotence X + X’ = 1 -- Complement X • X’ = 0 -- Complement (X’)’ = X -- Involution 12/29/2021 10: 13 PM Boolean Algebra PJF - 29

Duality • The dual of an expression is obtained by exchanging ( • and +), and (1 and 0) in it, provided that the precedence of operations is not changed. • Cannot exchange x with x’ • Example: – Find H(x, y, z), the dual of F(x, y, z) = x’yz’ + x’y’z – H = (x’+y+z’) (x’+y’+ z) 12/29/2021 10: 13 PM Boolean Algebra PJF - 30

Duality (cont’d) With respect to duality, Identities 1 – 8 have the following relationship: 1. X+0=X 2. X • 1 =X (dual of 1) 3. X+1 =1 4. X • 0 =0 (dual of 3) 5. X+X=X 6. X • X = X (dual of 5) 7. X + X’ = 1 8. X • X’ = 0 (dual of 8) 12/29/2021 10: 13 PM Boolean Algebra PJF - 31

More Boolean Algebra Properties Let X, Y, and Z: boolean variables X+Y=Y+X 12. X + (Y+Z) = (X+Y) + Z 14. X • (Y+Z) = X • Y + X • Z 10. 16. (X + Y)’ = X’ • Y’ X • Y=Y • X -- Commutative 13. X • (Y • Z) = (X • Y) • Z -- Associative 15. X+(Y • Z) = (X+Y) • (X+Z) 11. -- Distributive 17. (X • Y)’ = X’ + Y’ -- De. Morgan’s In general, ( X 1 + X 2 + … + Xn )’ = X 1’ • X 2’ • … • Xn’, and ( X 1 • X 2 • … • Xn )’ = X 1’ + X 2’ + … + Xn’ 12/29/2021 10: 13 PM Boolean Algebra PJF - 32

Absorption Property 1. x + x • y = x 2. x • (x+y) = x (dual) • Proof: x + x • y = x • 1 + x • y = x • (1+y) = x • 1 =x QED (2 true by duality, why? ) 12/29/2021 10: 13 PM Boolean Algebra PJF - 33

Consensus Theorem 1. xy + x’z + yz = xy + x’z 2. (x+y) • (x’+z) • (y+z) = (x+y) • (x’+z) -- (dual) • Proof: xy + x’z + yz = xy + x’z + (x+x’)yz = xy + x’z + xyz + x’yz = (xy + xyz) + (x’z + x’zy) = xy + x’z QED (2 true by duality). 12/29/2021 10: 13 PM Boolean Algebra PJF - 34

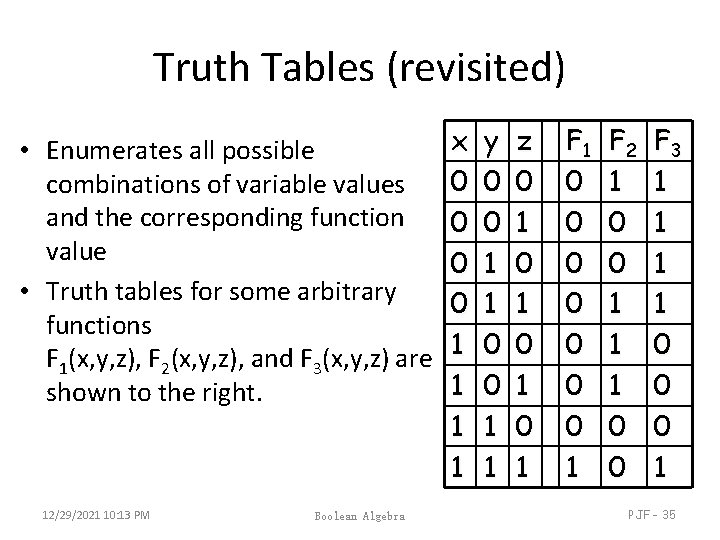
Truth Tables (revisited) • Enumerates all possible combinations of variable values and the corresponding function value • Truth tables for some arbitrary functions F 1(x, y, z), F 2(x, y, z), and F 3(x, y, z) are shown to the right. 12/29/2021 10: 13 PM Boolean Algebra x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 F 1 0 0 0 0 1 F 2 1 0 0 1 1 1 0 0 F 3 1 1 0 0 0 1 PJF - 35

Truth Tables (cont. ) • Truth table: a unique representation of a Boolean function • If two functions have identical truth tables, the functions are equivalent (and vice-versa). • Truth tables can be used to prove equality theorems. • However, the size of a truth table grows exponentially with the number of variables involved, hence unwieldy. This motivates the use of Boolean Algebra. 12/29/2021 10: 13 PM Boolean Algebra PJF - 36

Boolean expressions-NOT unique • Unlike truth tables, expressions representing a Boolean function are NOT unique. • Example: – F(x, y, z) = x’ • y’ • z’ + x’ • y • z’ + x • y • z’ – G(x, y, z) = x’ • y’ • z’ + y • z’ • The corresponding truth tables for F() and G() are to the right. They are identical. • Thus, F() = G() 12/29/2021 10: 13 PM Boolean Algebra x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 F 1 0 0 0 1 0 G 1 0 0 0 1 0 PJF - 37

Algebraic Manipulation • Boolean algebra is a useful tool for simplifying digital circuits. • Why do it? Simpler can mean cheaper, smaller, faster. • Example: Simplify F = x’yz + x’yz’ + xz = x’y(z+z’) + xz = x’y • 1 + xz = x’y + xz 12/29/2021 10: 13 PM Boolean Algebra PJF - 38

Algebraic Manipulation (cont. ) • Example: Prove x’y’z’ + x’yz’ + xyz’ = x’z’ + yz’ • Proof: x’y’z’+ x’yz’+ xyz’ = x’y’z’ + x’yz’ + xyz’ = x’z’(y’+y) + yz’(x’+x) = x’z’ • 1 + yz’ • 1 = x’z’ + yz’ QED. 12/29/2021 10: 13 PM Boolean Algebra PJF - 39

Complement of a Function • The complement of a function is derived by interchanging ( • and +), and (1 and 0), and complementing each variable. • Otherwise, interchange 1 s to 0 s in the truth table column showing F. • The complement of a function IS NOT THE SAME as the dual of a function. 12/29/2021 10: 13 PM Boolean Algebra PJF - 40

Complementation: Example • Find G(x, y, z), the complement of F(x, y, z) = xy’z’ + x’yz • G = F’ = (xy’z’ + x’yz)’ = (xy’z’)’ • (x’yz)’ De. Morgan = (x’+y+z) • (x+y’+z’) De. Morgan again • Note: The complement of a function can also be derived by finding the function’s dual, and then complementing all of the literals 12/29/2021 10: 13 PM Boolean Algebra PJF - 41

Canonical and Standard Forms • We need to consider formal techniques for the simplification of Boolean functions. – Identical functions will have exactly the same canonical form. – Minterms and Maxterms – Sum-of-Minterms and Product-of- Maxterms – Product and Sum terms – Sum-of-Products (SOP) and Product-of-Sums (POS) 12/29/2021 10: 13 PM Boolean Algebra PJF - 42

Definitions Literal: A variable or its complement Product term: literals connected by • Sum term: literals connected by + Minterm: a product term in which all the variables appear exactly once, either complemented or uncomplemented • Maxterm: a sum term in which all the variables appear exactly once, either complemented or uncomplemented • • 12/29/2021 10: 13 PM Boolean Algebra PJF - 43

Minterm • Represents exactly one combination in the truth table. • Denoted by mj, where j is the decimal equivalent of the minterm’s corresponding binary combination (bj). • A variable in mj is complemented if its value in bj is 0, otherwise is uncomplemented. • Example: Assume 3 variables (A, B, C), and j=3. Then, bj = 011 and its corresponding minterm is denoted by mj = A’BC 12/29/2021 10: 13 PM Boolean Algebra PJF - 44

Maxterm • Represents exactly one combination in the truth table. • Denoted by Mj, where j is the decimal equivalent of the maxterm’s corresponding binary combination (bj). • A variable in Mj is complemented if its value in bj is 1, otherwise is uncomplemented. • Example: Assume 3 variables (A, B, C), and j=3. Then, bj = 011 and its corresponding maxterm is denoted by Mj = A+B’+C’ 12/29/2021 10: 13 PM Boolean Algebra PJF - 45

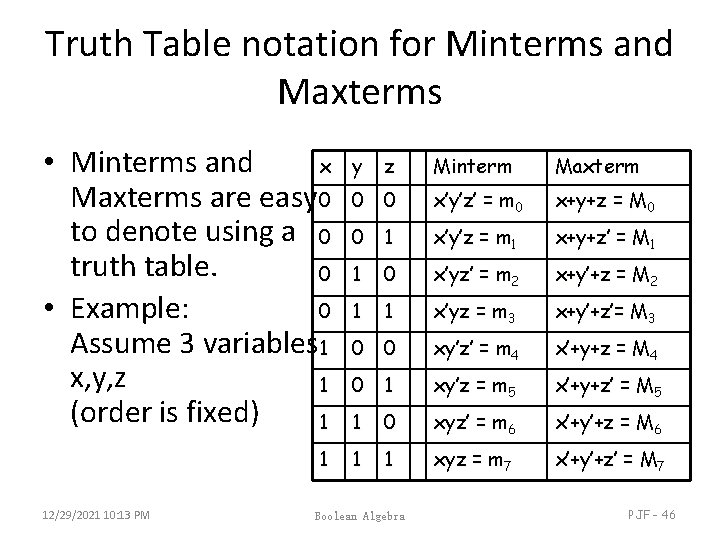
Truth Table notation for Minterms and Maxterms • Minterms and x Maxterms are easy 0 to denote using a 0 truth table. 0 • Example: 0 Assume 3 variables 1 x, y, z 1 (order is fixed) 1 y 1 12/29/2021 10: 13 PM z Minterm Maxterm 0 0 x’y’z’ = m 0 x+y+z = M 0 0 1 x’y’z = m 1 x+y+z’ = M 1 1 0 x’yz’ = m 2 x+y’+z = M 2 1 1 x’yz = m 3 x+y’+z’= M 3 0 0 xy’z’ = m 4 x’+y+z = M 4 0 1 xy’z = m 5 x’+y+z’ = M 5 1 0 xyz’ = m 6 x’+y’+z = M 6 1 1 xyz = m 7 x’+y’+z’ = M 7 Boolean Algebra PJF - 46

Canonical Forms (Unique) • Any Boolean function F( ) can be expressed as a unique sum of minterms and a unique product of maxterms (under a fixed variable ordering). • In other words, every function F() has two canonical forms: – Canonical Sum-Of-Products (sum of minterms) – Canonical Product-Of-Sums (product of maxterms) 12/29/2021 10: 13 PM Boolean Algebra PJF - 47

Canonical Forms (cont. ) • Canonical Sum-Of-Products: The minterms included are those mj such that F( ) = 1 in row j of the truth table for F( ). • Canonical Product-Of-Sums: The maxterms included are those Mj such that F( ) = 0 in row j of the truth table for F( ). 12/29/2021 10: 13 PM Boolean Algebra PJF - 48

Example • Truth table for f 1(a, b, c) at right a • The canonical sum-of-products form for f 1 is 0 f 1(a, b, c) = m 1 + m 2 + m 4 + m 6 = a’b’c + a’bc’ + ab’c’ + abc’ 0 • The canonical product-of-sums form for f 1 is 0 f 1(a, b, c) = M 0 • M 3 • M 5 • M 7 0 = (a+b+c) • (a+b’+c’) • (a’+b’+c’). 1 • Observe that: mj = Mj’ b 0 0 1 1 12/29/2021 10: 13 PM Boolean Algebra c 0 1 0 1 f 1 0 1 0 1 0 PJF - 49

Shorthand: ∑ and ∏ • f 1(a, b, c) = ∑ m(1, 2, 4, 6), where ∑ indicates that this is a sum-of-products form, and m(1, 2, 4, 6) indicates that the minterms to be included are m 1, m 2, m 4, and m 6. • f 1(a, b, c) = ∏ M(0, 3, 5, 7), where ∏ indicates that this is a product-of-sums form, and M(0, 3, 5, 7) indicates that the maxterms to be included are M 0, M 3, M 5, and M 7. • Since mj = Mj’ for any j, ∑ m(1, 2, 4, 6) = ∏ M(0, 3, 5, 7) = f 1(a, b, c) 12/29/2021 10: 13 PM Boolean Algebra PJF - 50

Conversion Between Canonical Forms • Replace ∑ with ∏ (or vice versa) and replace those j’s that appeared in the original form with those that do not. • Example: f 1(a, b, c) = a’b’c + a’bc’ + ab’c’ + abc’ = m 1 + m 2 + m 4 + m 6 = ∑(1, 2, 4, 6) = ∏(0, 3, 5, 7) = (a+b+c) • (a+b’+c’) • (a’+b’+c’) 12/29/2021 10: 13 PM Boolean Algebra PJF - 51

Standard Forms (NOT Unique) • Standard forms are “like” canonical forms, except that not all variables need appear in the individual product (SOP) or sum (POS) terms. • Example: f 1(a, b, c) = a’b’c + bc’ + ac’ is a standard sum-of-products form • f 1(a, b, c) = (a+b+c) • (b’+c’) • (a’+c’) is a standard product-of-sums form. 12/29/2021 10: 13 PM Boolean Algebra PJF - 52

Conversion of SOP from standard to canonical form • Expand non-canonical terms by inserting equivalent of 1 in each missing variable x: (x + x’) = 1 • Remove duplicate minterms • f 1(a, b, c) = a’b’c + bc’ + ac’ = a’b’c + (a+a’)bc’ + a(b+b’)c’ = a’b’c + abc’ + a’bc’ + ab’c’ = a’b’c + abc’ + a’bc + ab’c’ 12/29/2021 10: 13 PM Boolean Algebra PJF - 53

Conversion of POS from standard to canonical form • Expand noncanonical terms by adding 0 in terms of missing variables (e. g. , xx’ = 0) and using the distributive law • Remove duplicate maxterms • f 1(a, b, c) = (a+b+c) • (b’+c’) • (a’+c’) = (a+b+c) • (aa’+b’+c’) • (a’+bb’+c’) = (a+b+c) • (a+b’+c’) • (a’+b+c’) • (a’+b’+c’) = (a+b+c) • (a+b’+c’) • (a’+b+c’) 12/29/2021 10: 13 PM Boolean Algebra PJF - 54