Transient Water Balance Eqn Inflow Outflow S Recharge

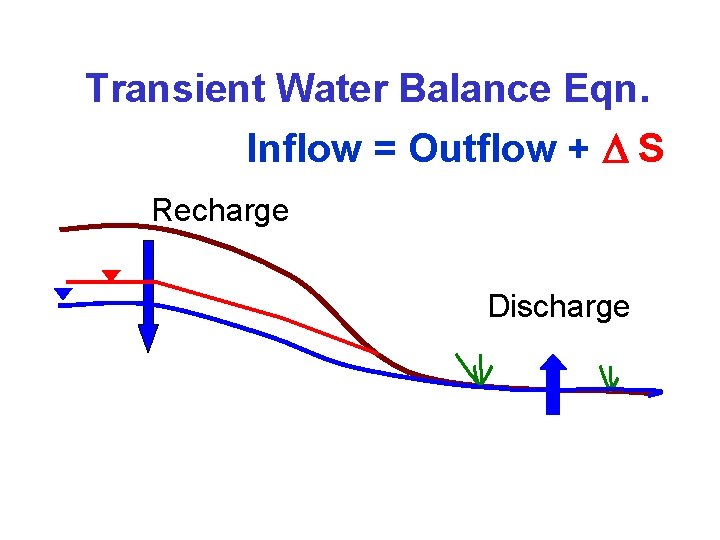
Transient Water Balance Eqn. Inflow = Outflow + S Recharge Discharge

OUT – IN = x y z = change in storage = - V/ t Ss = V / ( x y z h) V = Ss h ( x y z) t t

OUT – IN = General governing equation for transient, heterogeneous, and anisotropic conditions

Law of Mass Balance + Darcy’s Law = Governing Equation for Groundwater Flow -------------------------------div q = - Ss ( h t) +W (Law of Mass Balance) q = - K grad h (Darcy’s Law) div (K grad h) = Ss ( h t) – W

2 D profile 2 D confined 2 D unconfined Storage coefficient is either storativity (S) or specific yield (Sy). S = Ss b (& Tx = Kx b; Ty= Ky b) Ss is specific storage.

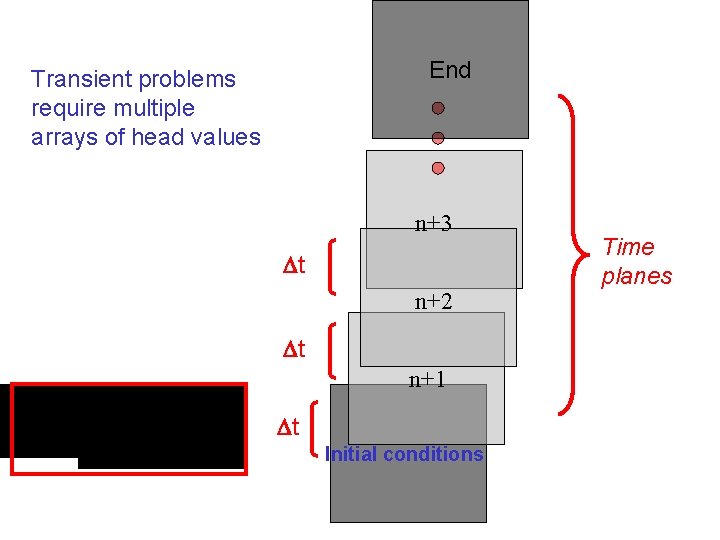
End Transient problems require multiple arrays of head values n+3 t n+2 t n+1 t Initial conditions Time planes

2 D confined 1 D, transient, homogeneous, isotropic, confined, no sink/source term

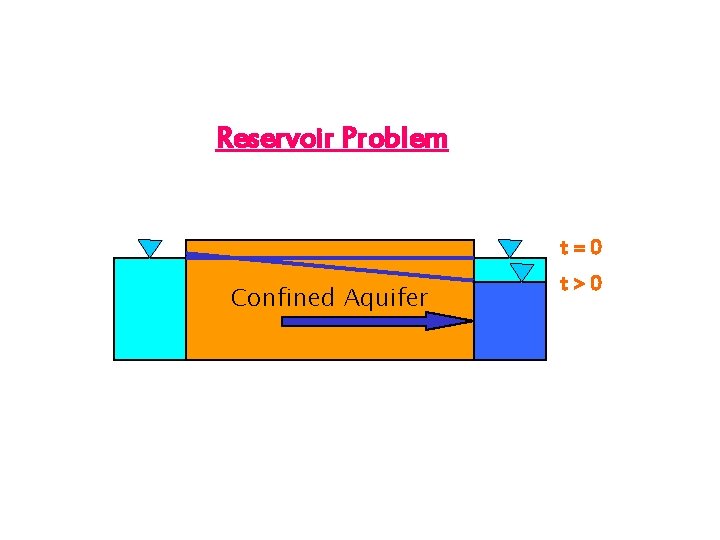
Reservoir Problem t=0 Confined Aquifer 1 D, transient t>0

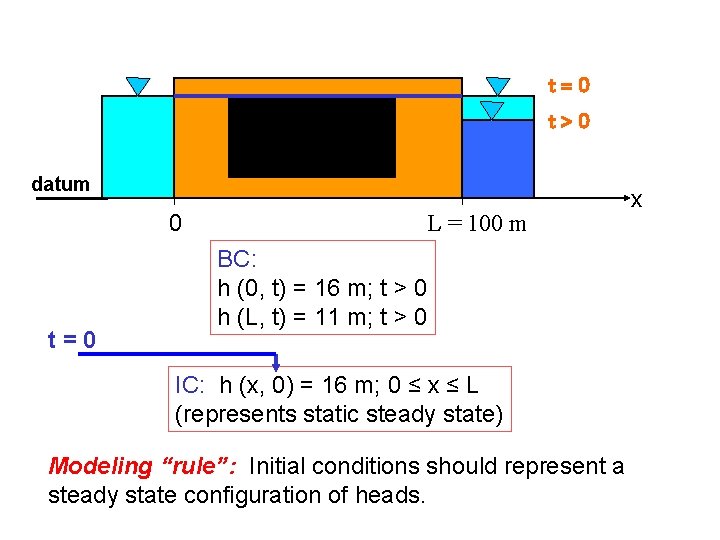
t=0 t>0 datum 0 t=0 L = 100 m BC: h (0, t) = 16 m; t > 0 h (L, t) = 11 m; t > 0 IC: h (x, 0) = 16 m; 0 ≤ x ≤ L (represents static steady state) Modeling “rule”: Initial conditions should represent a steady state configuration of heads. x

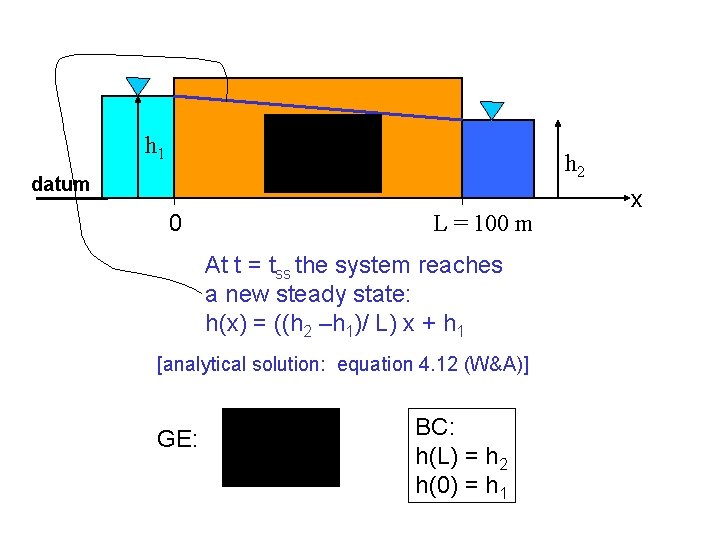
h 1 h 2 datum 0 L = 100 m At t = tss the system reaches a new steady state: h(x) = ((h 2 –h 1)/ L) x + h 1 [analytical solution: equation 4. 12 (W&A)] GE: BC: h(L) = h 2 h(0) = h 1 x

Governing Eqn. for transient Reservoir Problem 1 D, transient, homogeneous, isotropic, confined, no sink/source term i-1, j i-1/2 i, j i+1/2 i+1, j

Explicit Approximation

Explicit Solution Eqn. 4. 11 (W&A) Everything on the RHS of the equation is known. Solve explicitly for ; no iteration is needed.

• Explicit approximations are unstable unless small time steps are used. • We can derive the stability criterion by writing the explicit approx. in a form that looks like the SOR iteration formula and setting the terms in the position occupied by equal to 1. • For the 1 D governing equation used in the reservoir problem, the stability criterion is: or

For the reservoir problem: T = 0. 02 m 2/min S = 0. 002 x = 10 m

Explicit Solution

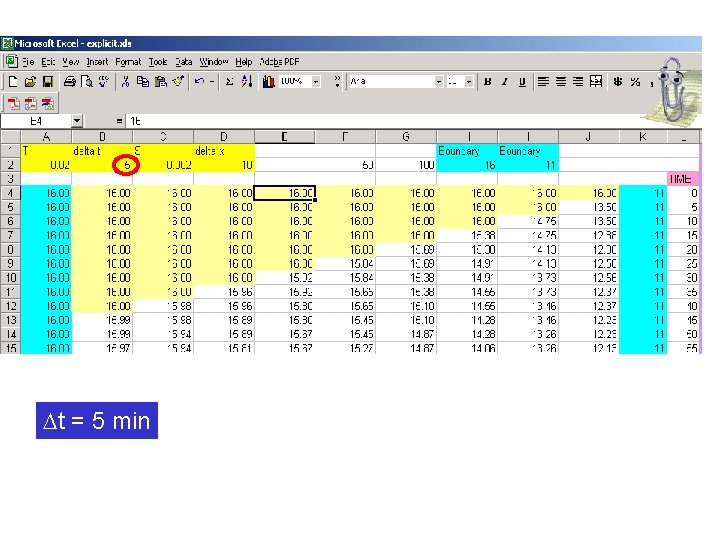
t = 5 min

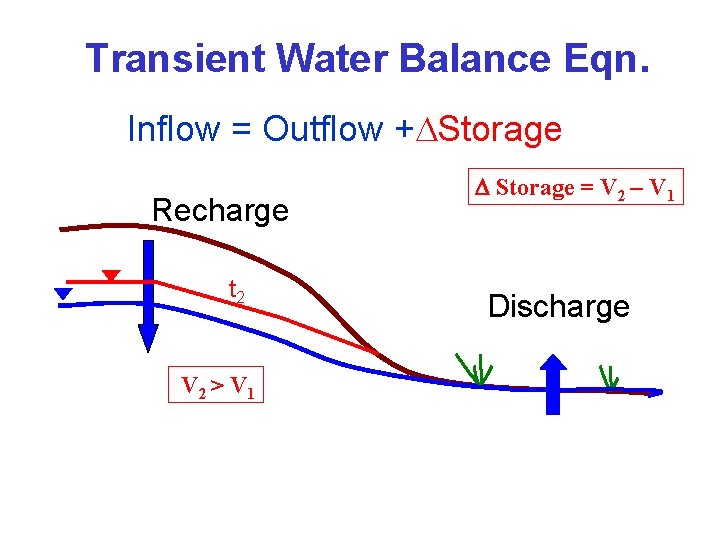
Transient Water Balance Eqn. Inflow = Outflow + Storage Recharge t 2 V 2 > V 1 Storage = V 2 – V 1 Discharge

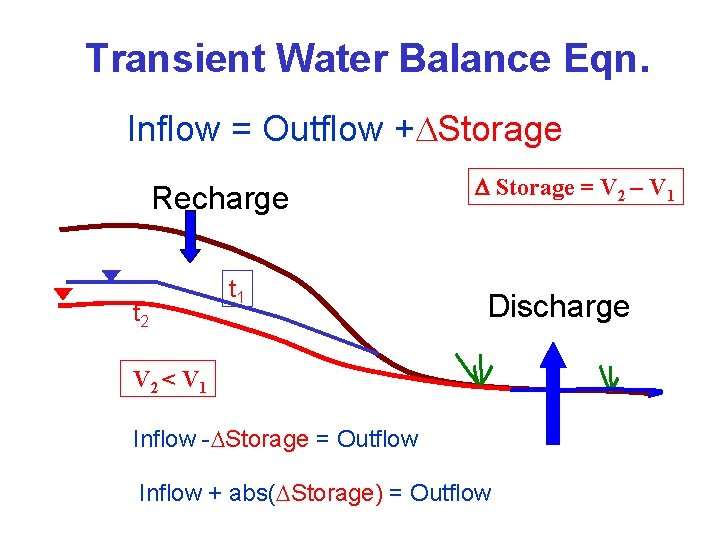
Transient Water Balance Eqn. Inflow = Outflow + Storage Recharge t 2 t 1 Storage = V 2 – V 1 Discharge V 2 < V 1 Inflow - Storage = Outflow Inflow + abs( Storage) = Outflow

Water Balance- version 1 Storage = V(t 2)- V(t 1) IN > OUT then water going into storage and Storage is + OUT > IN then water is coming out of storage and Storage is – IN – OUT= Storage Total IN Total OUT Flow in ABS(Flow out) ABS( Storage) Storage Total IN = Total Out MODFLOW Convention: Water coming out of storage goes into the aquifer (IN column). Water going into storage comes out of the aquifer (OUT column).

Water Balance- version 2 Storage = V(t 1)- V(t 2) IN > OUT then water going into storage and Storage is OUT > IN then water is coming out of storage and Storage is + IN - OUT = Storage Total IN(+) Total OUT(-) Flow in Flow out Storage Convention: Water coming out of storage goes into the aquifer (IN column). Water going into storage comes out of the aquifer (OUT column). Total IN = ABS(Total Out)

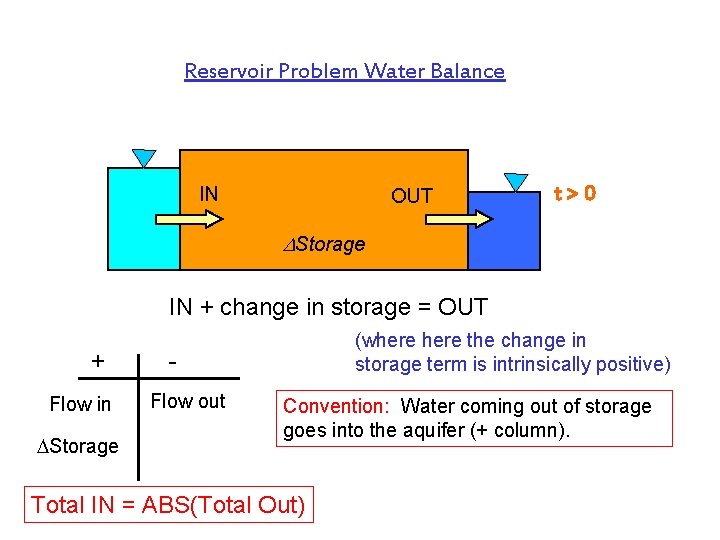
Reservoir Problem Water Balance IN OUT t>0 Storage IN + change in storage = OUT + Flow in Storage (where the change in storage term is intrinsically positive) Flow out Convention: Water coming out of storage goes into the aquifer (+ column). Total IN = ABS(Total Out)

Units + Flow in Flow out Storage L 3/T (m 3/min)

OUT – IN = x y z = change in storage = - V/ t Ss = V / ( x y z h) V = Ss h ( x y z) t t

Storage Term for the Water Balance 3 D problem: V = Ss h ( x y z) t t 2 D problem: V = S h ( x y) t t where S = Ss b In 1 D Reservoir Problem, y is taken to be equal to 1.

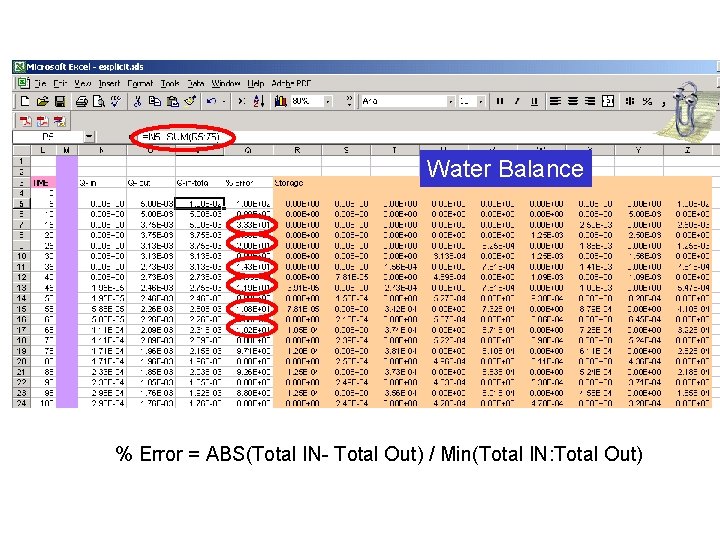
Water Balance % Error = ABS(Total IN- Total Out) / Min(Total IN: Total Out)

Stablity criterion for explicit solution: For the reservoir problem: T = 0. 02 m 2/min S = 0. 002 x = 10 m Judging by the water balance error, t = 5 min may be too large.