Transforms Basis to Basis Normal Basis Hadamard Basis
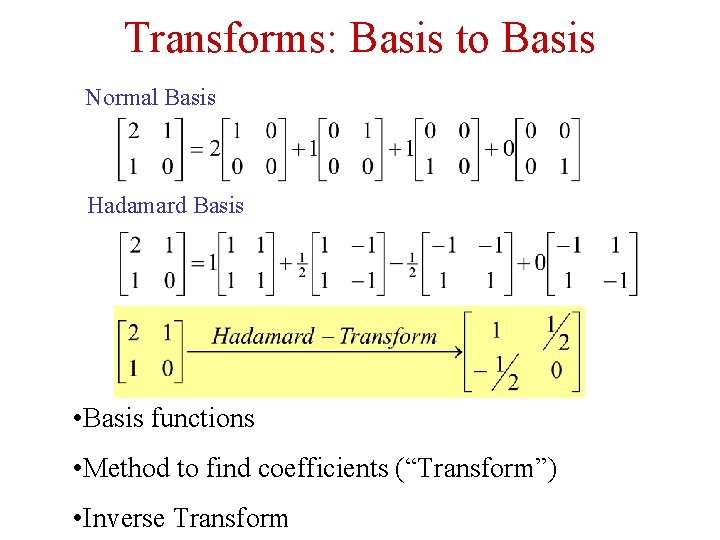
Transforms: Basis to Basis Normal Basis Hadamard Basis • Basis functions • Method to find coefficients (“Transform”) • Inverse Transform

Basis for a Vector Space • Every vector in the space is a linear combination of basis vectors. • n independent vectors from an nth dimensional vector space form a basis. • Orthogonal Basis: Every two basis vectors are Orthogonal. • Orthonormal Basis: The absolute value of all basis vectors is 1.

i Complex Numbers R b Absolute Value: a Phase:

Fourier Spectrum Fourier: Fourier Spectrum Fourier Phase Fourier:

Discrete Fourier Transform Inverse Fourier Transform Complexity: O(N 2) (106 1012) FFT: (106 107) O(N log. N)

2 D Discrete Fourier Transform Inverse Fourier Transform

Display Fourier Spectrum as Picture 1. Compute 2. Scale to full range 3. Move (0, 0) to center of image (Shift by N/2) Example for range 0. . 10: Original f Scaled to 10 0 0 1 0 2 0 4 0 10 Log (1+f) Scaled to 10 0 0 0. 69 1 1. 01 2 1. 61 4 4. 62 10

Decomposition

Decomposition (II) • 1 -D Fourier is sufficient to do 2 -D Fourier – Do 1 -D Fourier on each column. On result: – Do 1 -D Fourier on each row – (Multiply by N? ) • 1 -D Fourier Transform is enough to do Fourier for ANY dimension

Derivatives I Inverse Fourier Transform

Derivatives II • To compute the x derivative of f (up to a constant): – Computer the Fourier Transform F – Multiply each Fourier coefficient F(u, v) by u – Compute the Inverse Fourier Transform • To compute the y derivative of f (up to a constant): – Computer the Fourier Transform F – Multiply each Fourier coefficient F(u, v) by v – Compute the Inverse Fourier Transform

Translation

Periodicity & Symmetry

Rotation
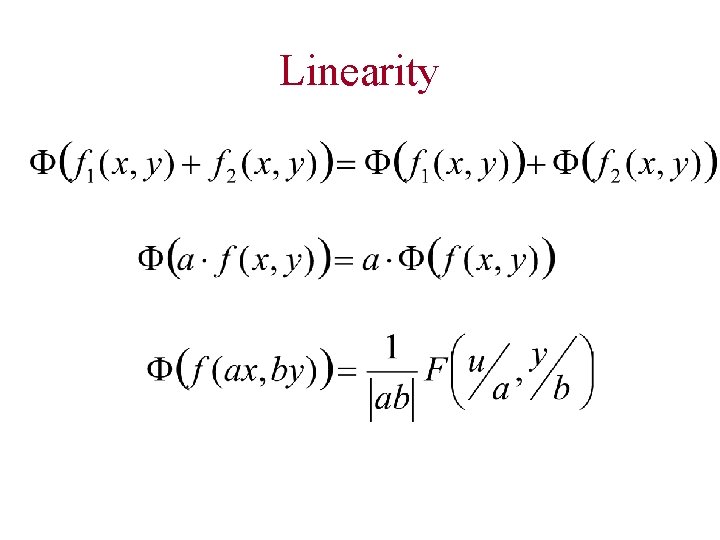
Linearity

Convolution Theorem Convolution by Fourier: Complexity of Convolution: O(N log. N)
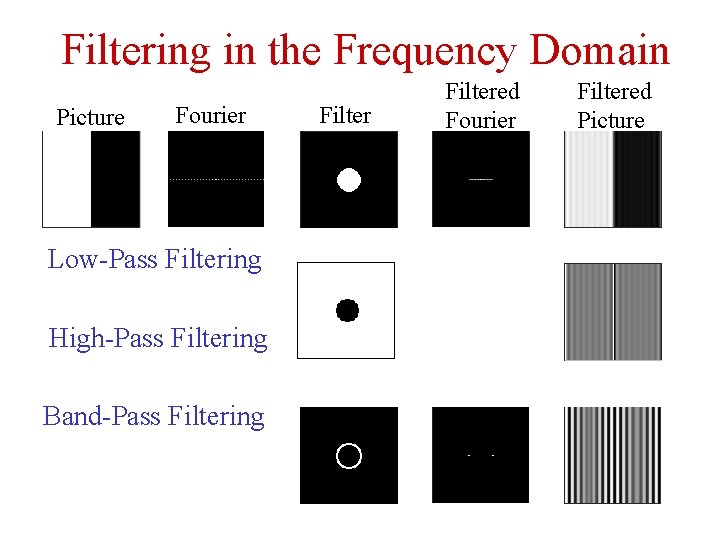
Filtering in the Frequency Domain Picture Fourier Low-Pass Filtering High-Pass Filtering Band-Pass Filtering Filtered Fourier Filtered Picture

Low Pass: Frequency & Image • (0 0 1 1 0 0) Sinc • (0 0 1 1 0 0) * (0 0 1 1 0 0 ) = (0 1 2 1 0 0) Sinc 2 • (0 1 4 6 4 1 0) = (0 0 1 1 0 0 ) 4 Sinc 4 • Fourier (Gaussian) Gaussian
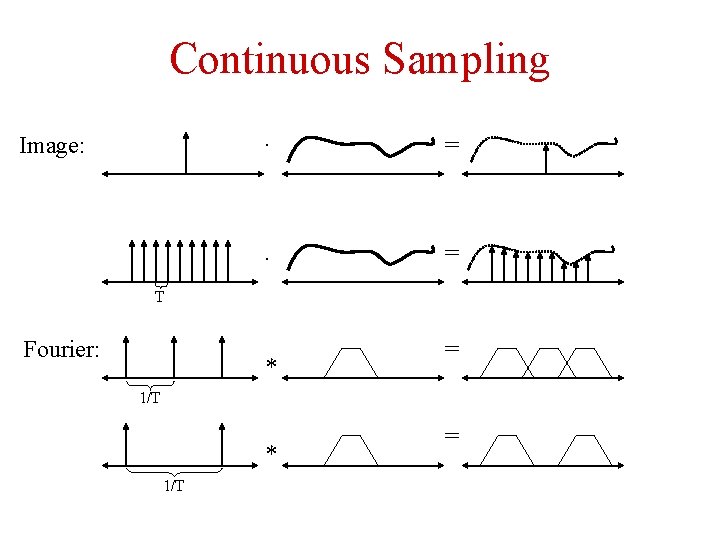
Continuous Sampling Image: · = T Fourier: * = 1/T * 1/T =
- Slides: 19