Transforms A sine wave 5sin 2 4 t




























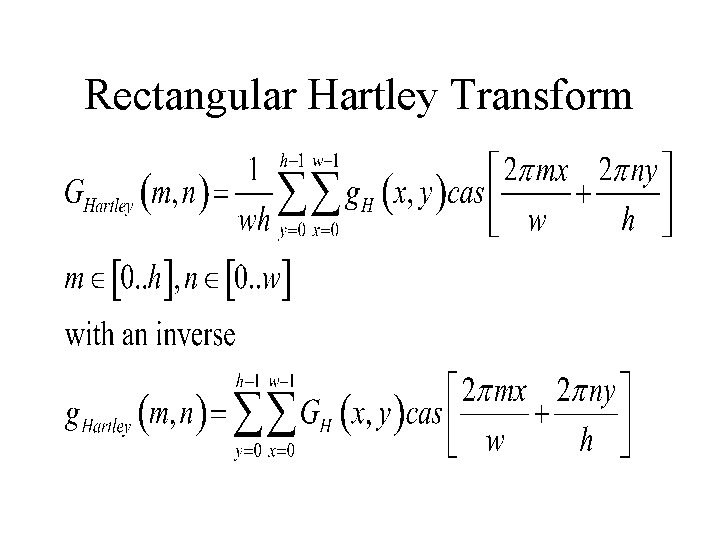













- Slides: 67

Transforms

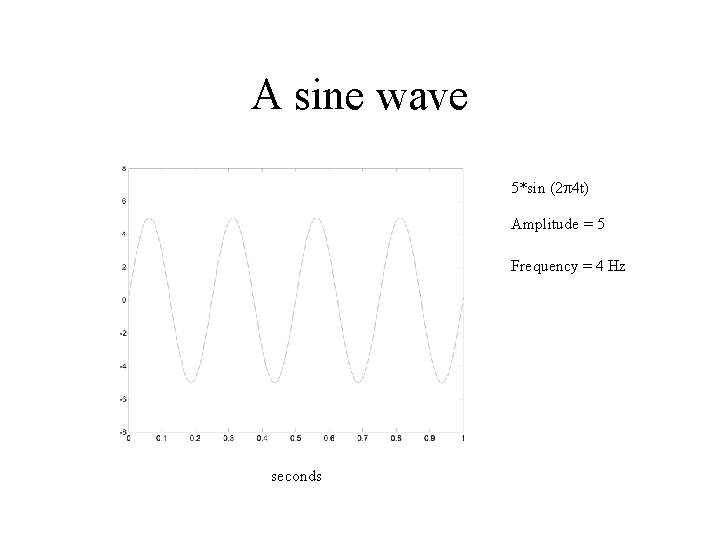
A sine wave 5*sin (2 4 t) Amplitude = 5 Frequency = 4 Hz seconds

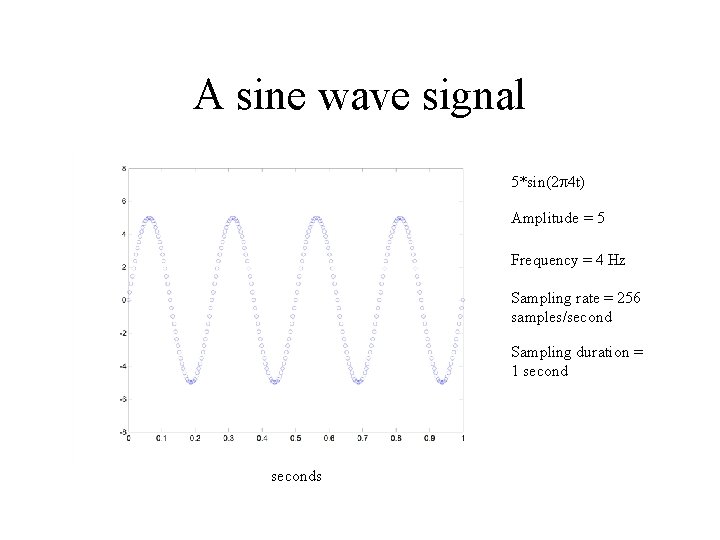
A sine wave signal 5*sin(2 4 t) Amplitude = 5 Frequency = 4 Hz Sampling rate = 256 samples/second Sampling duration = 1 seconds

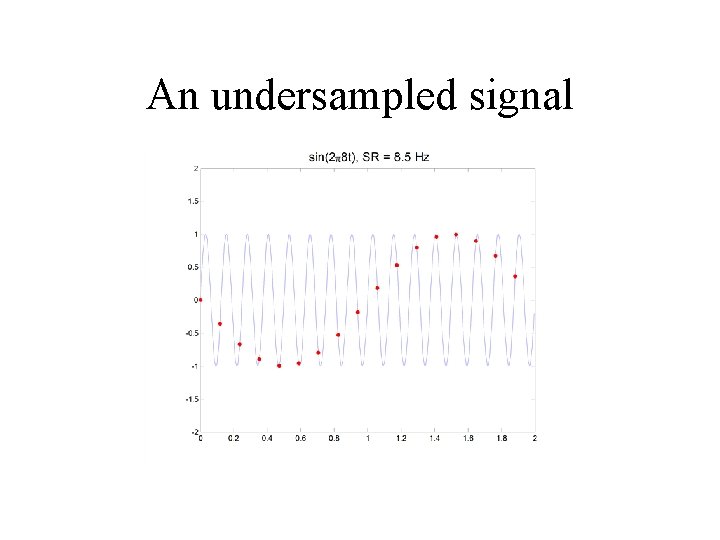
An undersampled signal

The Nyquist Frequency • The Nyquist frequency is equal to one-half of the sampling frequency. • The Nyquist frequency is the highest frequency that can be measured in a signal.

Fourier series • Periodic functions and signals may be expanded into a series of sine and cosine functions

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal)

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal) • Continuous Fourier Transform: close your eyes if you don’t like integrals

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal) • Continuous Fourier Transform:

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal) • The Discrete Fourier Transform:

Fast Fourier Transform • The Fast Fourier Transform (FFT) is a very efficient algorithm for performing a discrete Fourier transform • FFT principle first used by Gauss in 18? ? • FFT algorithm published by Cooley & Tukey in 1965 • In 1969, the 2048 point analysis of a seismic trace took 13 ½ hours. Using the FFT, the same task on the same machine took 2. 4 seconds!

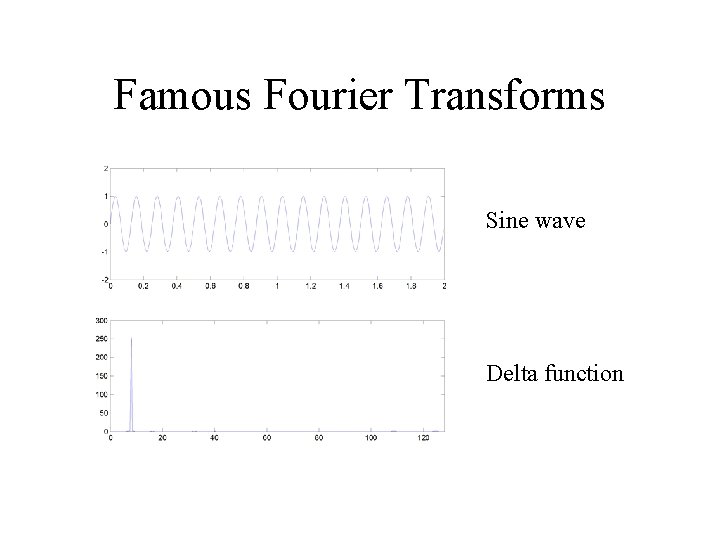
Famous Fourier Transforms Sine wave Delta function

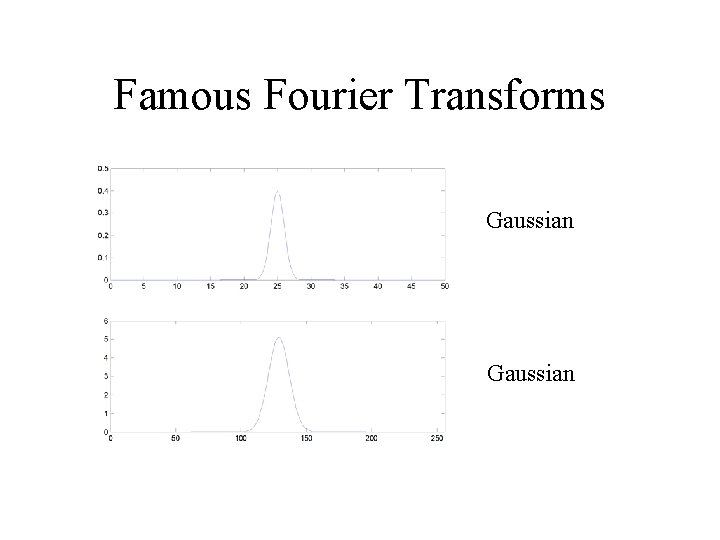
Famous Fourier Transforms Gaussian

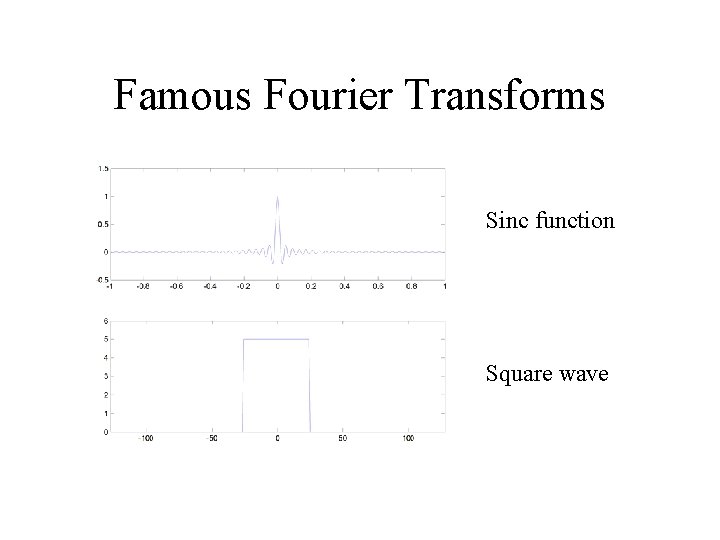
Famous Fourier Transforms Sinc function Square wave

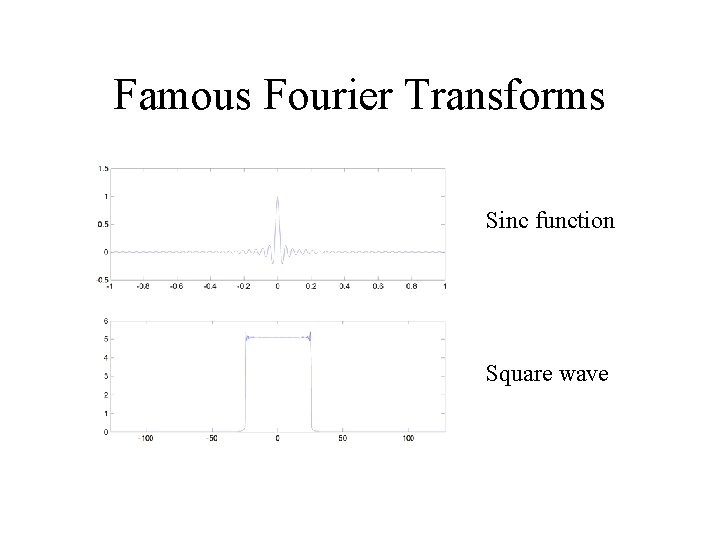
Famous Fourier Transforms Sinc function Square wave

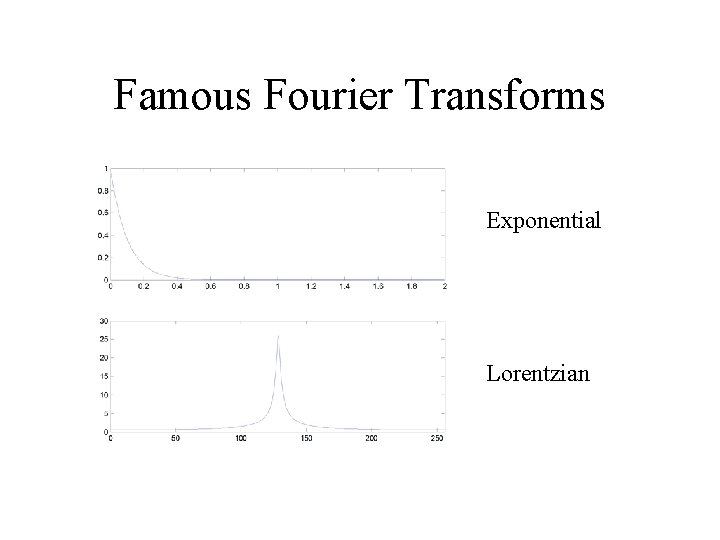
Famous Fourier Transforms Exponential Lorentzian

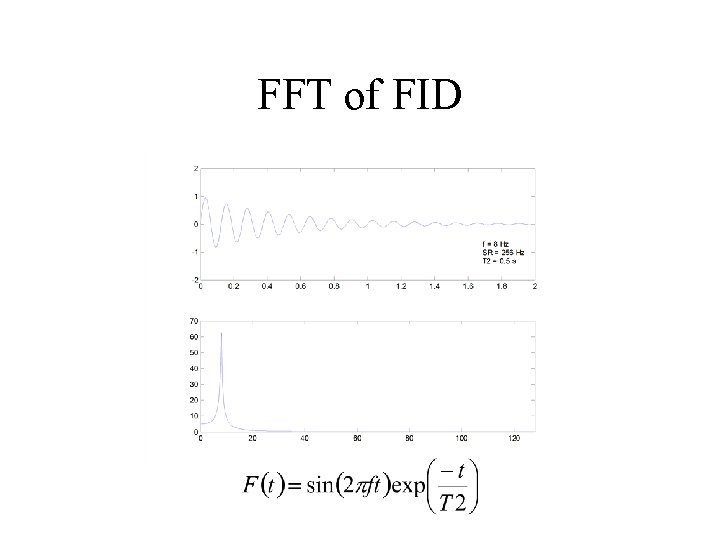
FFT of FID

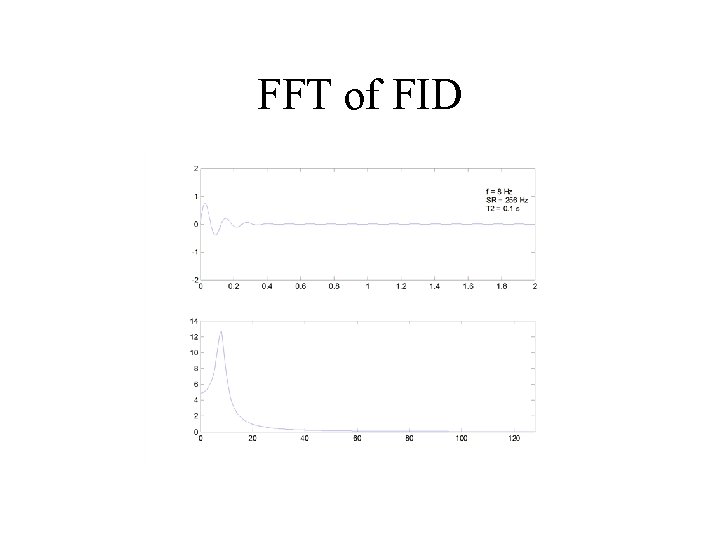
FFT of FID

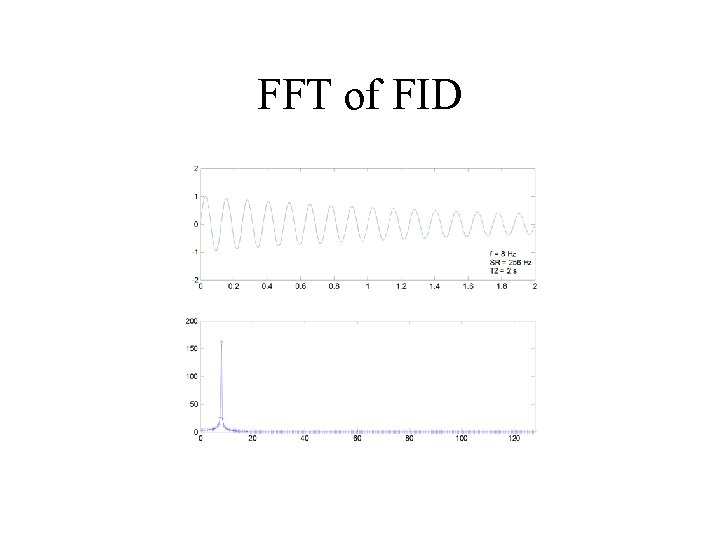
FFT of FID

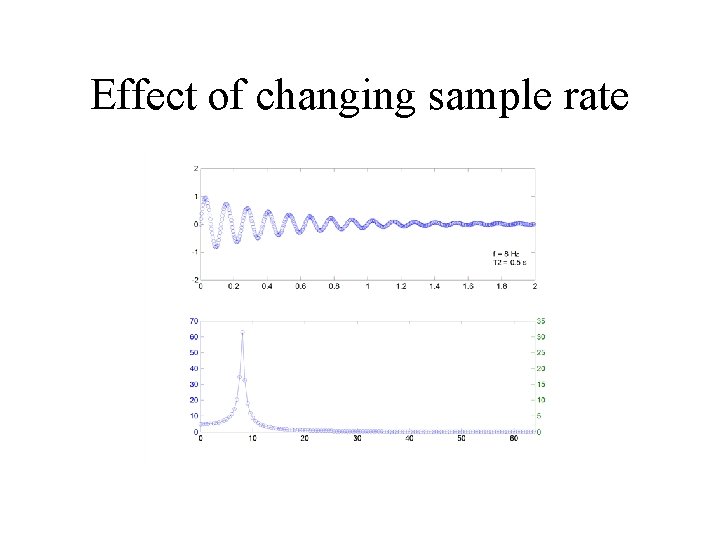
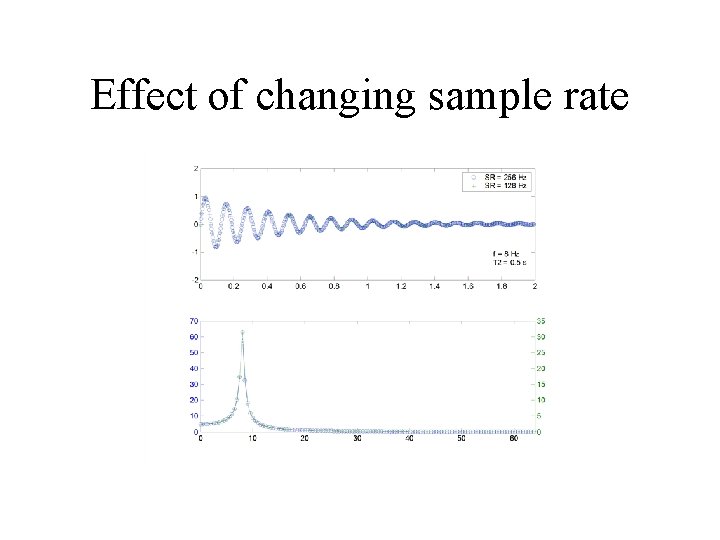
Effect of changing sample rate

Effect of changing sample rate

Effect of changing sample rate • Lowering the sample rate: – Reduces the Nyquist frequency, which – Reduces the maximum measurable frequency – Does not affect the frequency resolution

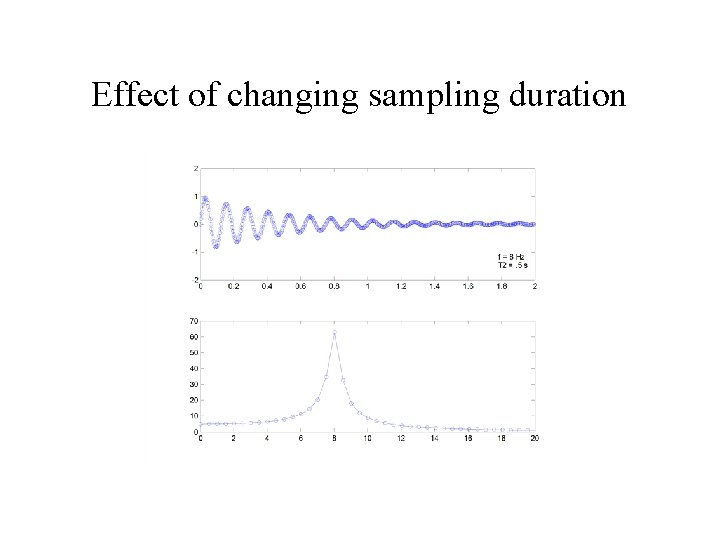
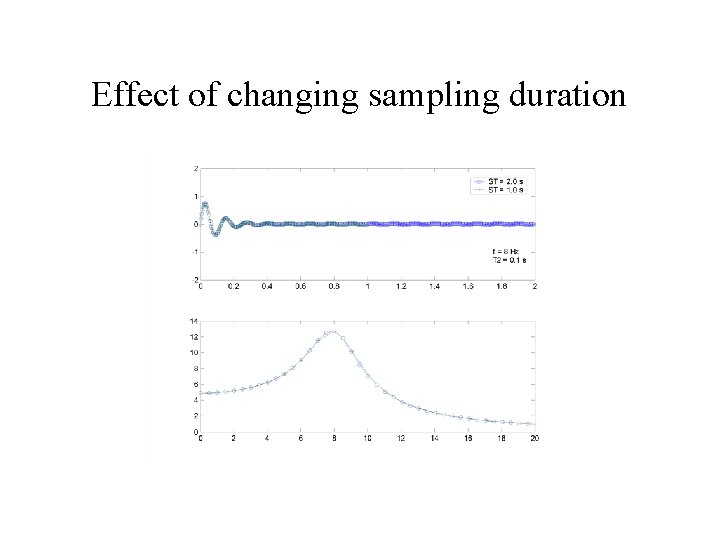
Effect of changing sampling duration

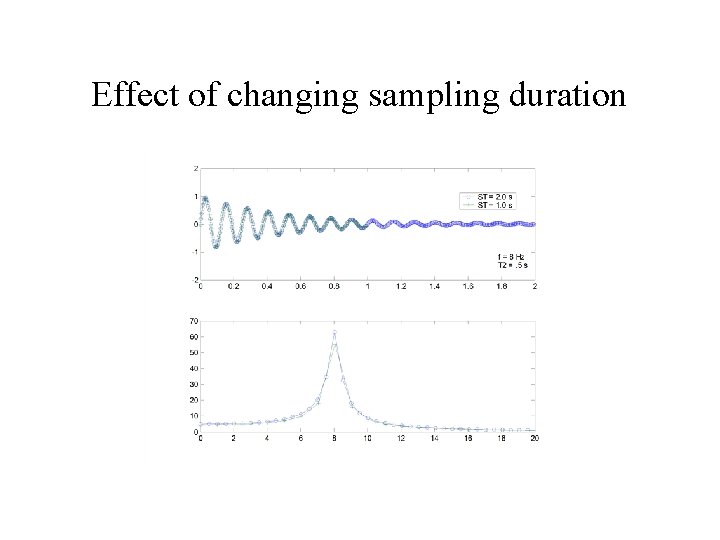
Effect of changing sampling duration

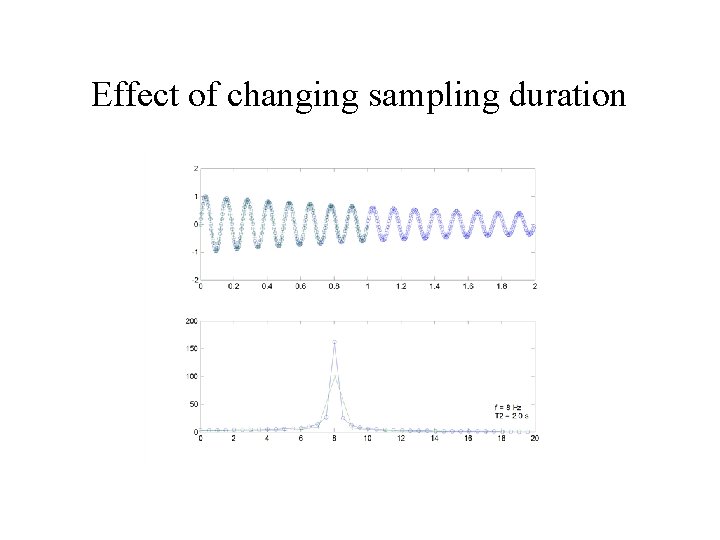
Effect of changing sampling duration • Reducing the sampling duration: – Lowers the frequency resolution – Does not affect the range of frequencies you can measure

Effect of changing sampling duration

Effect of changing sampling duration

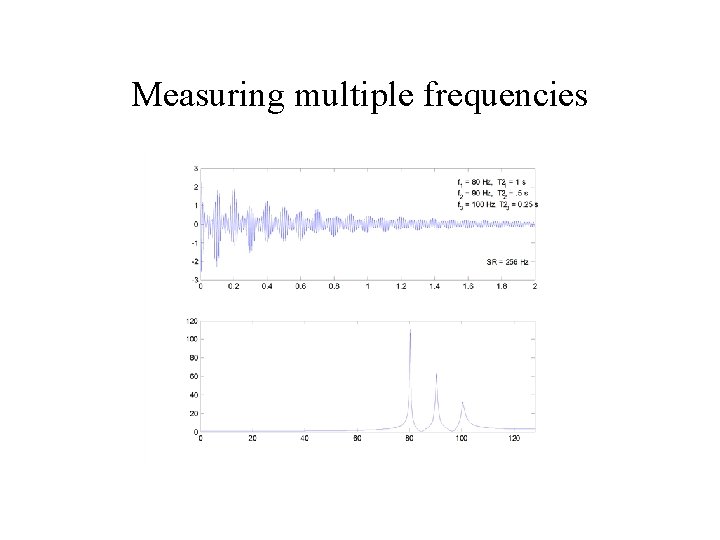
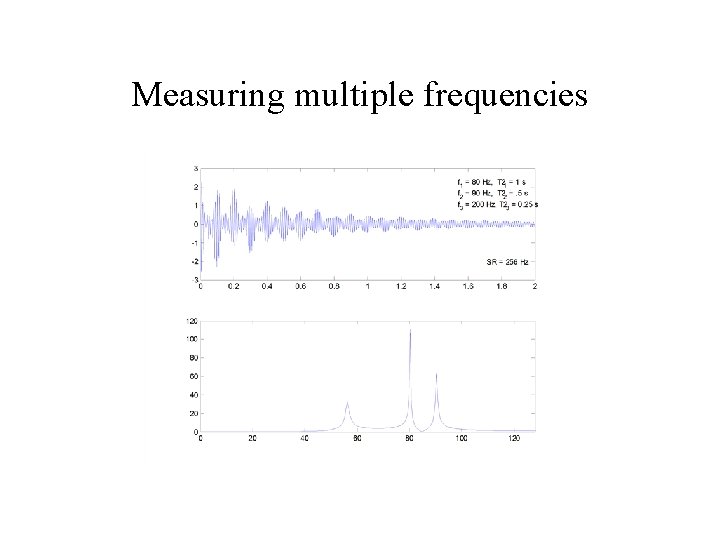
Measuring multiple frequencies

Measuring multiple frequencies


L: period; u and v are the number of cycles fitting into one horizontal and vertical period, respectively of f(x, y).

Discrete Fourier Transform

Discrete Fourier Transform (DFT). • When applying the procedure to images, we must deal explicitly with the fact that an image is: – Two-dimensional – Sampled – Of finite extent • These consideration give rise to the The DFT of an Nx. N image can be written:

Discrete Fourier Transform • For any particular spatial frequency specified by u and v, evaluating equation 8. 5 tell us how much of that particular frequency is present in the image. • There also exist an inverse Fourier Transform that convert a set of Fourier coefficients into an image.

PSD • The magnitudes correspond to the amplitudes of the basic images in our Fourier representation. • The array of magnitudes is termed the amplitude spectrum (or sometime ‘spectrum’). • The array of phases is termed the phase spectrum. • The power spectrum is simply the square of its amplitude spectrum:

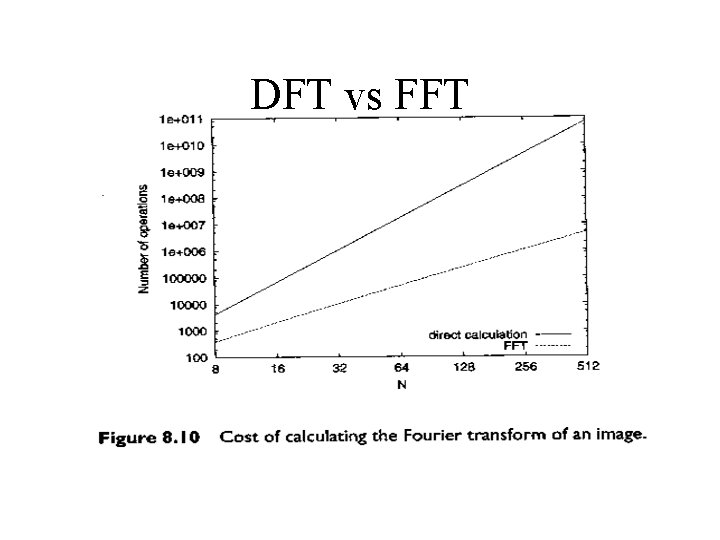
FFT • The Fast Fourier Transform is one of the most important algorithms ever developed – Developed by Cooley and Tukey in mid 60 s. – Is a recursive procedure that uses some cool math tricks to combine sub -problem results into the overall solution.

DFT vs FFT

DFT vs FFT

DFT vs FFT

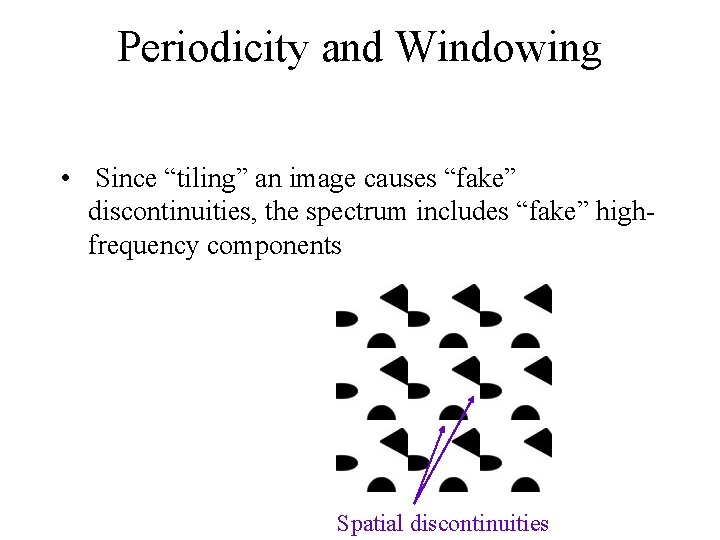
Periodicity assumption • The DFT assumes that an image is part of an infinitely repeated set of “tiles” in every direction. This is the same effect as “circular indexing”.

Periodicity and Windowing • Since “tiling” an image causes “fake” discontinuities, the spectrum includes “fake” highfrequency components Spatial discontinuities

Discrete Cosine Transform Real-valued

DCT in Matrix Form

Discrete Sine Transform Most Convenient when N=2 p - 1

DST in Matrix Form

DCT Basis Functions*

(Log Magnitude) DCT Example*

Hartley Transform • Alternative to Fourier • Produces N Real Numbers • Use Cosine Shifted 45 o to the Right

Square Hartley Transform
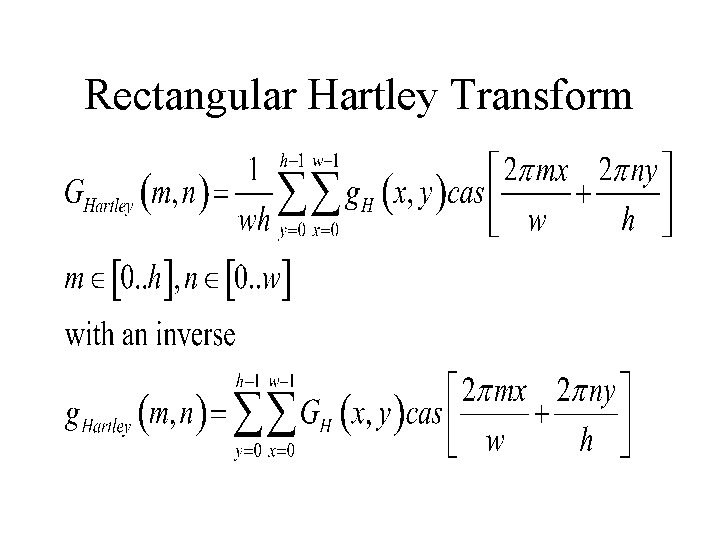
Rectangular Hartley Transform

Hartley in Matrix Form

What is an even function? • the function f is even if the following equation holds for all x in the domain of f:

Hartley Convolution Theorem • Computational Alternative to Fourier Transform • If One Function is Even, Convolution in one Domain is Multiplication in Hartley Domain

Rectangular Wave Transforms • Binary Valued {1, -1} • Fast to Compute • Examples – Hadamard – Walsh – Slant – Haar

Hadamard Transform • Consists of elements of +/- 1 • A Normalized N x N Hadamard matrix satisfies the relation H Ht = I

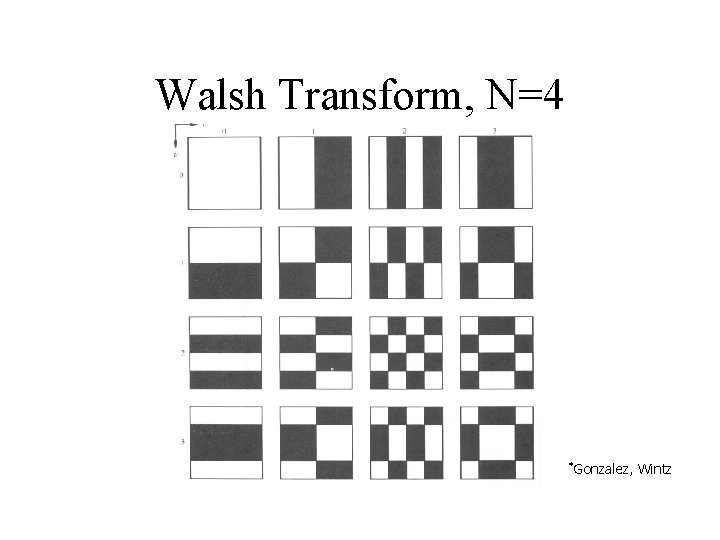
Walsh Transform, N=4 *Gonzalez, Wintz

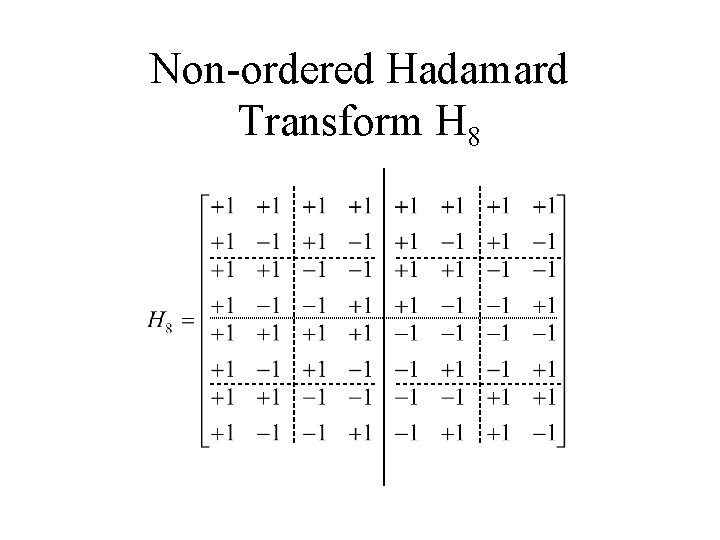
Non-ordered Hadamard Transform H 8

Sequency • In a Hadamard Transform, the Number of Sign Changes in a Row Divided by Two • It is Possible to Construct an H matrix with Increasing Sequency per row

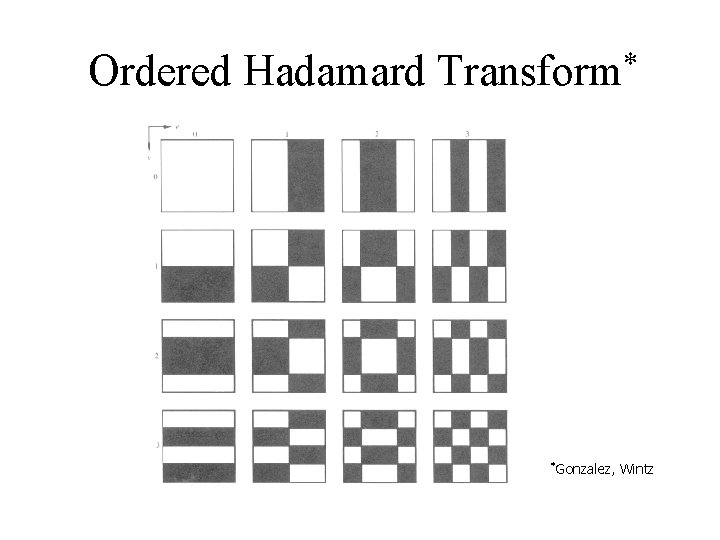
Ordered Hadamard Transform

Ordered Hadamard * Transform *Gonzalez, Wintz

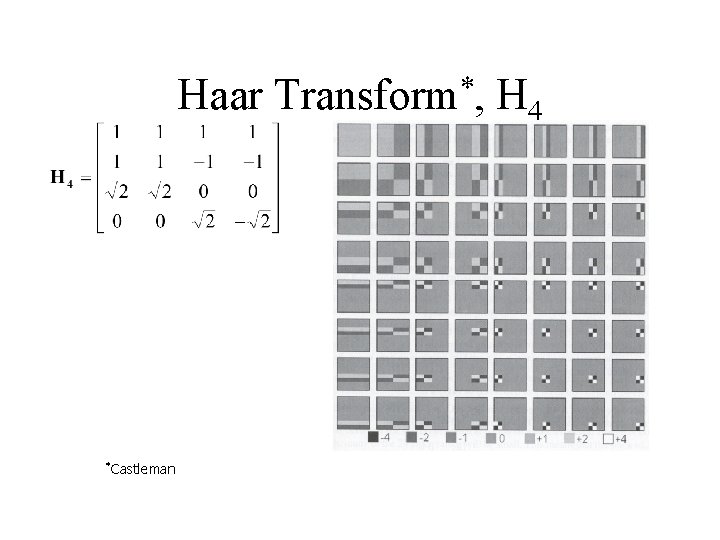
Haar Transform • Derived from Haar Matrix • Sampling Process in which Subsequent Rows Sample the Input Data with Increasing Resolution • Different Types of Differential Energy Concentrated in Different Regions – Power taken two at a time – Power taken a power of two at a time, etc.

Haar *Castleman * Transform , H 4

Karhunen-Loeve Transform • Variously called the K-L, Hotelling, or Eignevector • Continuous Form Developed by K-L • Discrete Version Credited to Hotelling • Transforms a Signal into a Set of Uncorrelated Representational Coefficients • Keep Largest Coefficients for Image Compression

Discrete K-L

Singular Value Decomposition

Singular Value Decomposition • If A is symmetric, then U=V • Kernel Depends on Image Being Transformed • Need to Compute AAt and At. A and Find the Eigenvalues • Small Values can be Ignored to Yield Compression

Transform Domain Filtering • Similar to Fourier Domain Filtering • Applicable to Images in which Noise is More Easily Represented in Domain other than Fourier – Vertical and horizontal line detection: Haar transform produces non-zero entries in first row and/or first column