Transformations We want to be able to make

Transformations • We want to be able to make changes to the image • larger/smaller • rotate • move • This can be efficiently achieved through mathematical operations known as transformations

Transformations • We will transform the endpoints only • If we then draw the (new) lines between the transformed endpoints, we get the transformed image • This only works for certain types of transformations known as affine transformations • Such transformations preserve lines and distances and relative proportions • i. e. , points on the same line before remain on the same line after an affine transformation

Transformations • Three transformations that fall into this category are • Scaling • Rotation • Translation

But First… • We’re going to need a bit of math… • … just enough to get the general idea

Matrices • Matrix • 2 dimensional array (of numbers) • m x n matrix • m rows • n columns

Matrices • Matrix • 2 dimensional array (of numbers) • m x n matrix 2 rows • m rows • n columns • xij is the entry at row I, column j 3 columns

Some Examples • 1 x 2 matrix • a 2 x 1 matrix • 2 x 2 matrix • A 3 x 3 matrix

Matrix Multiplication • In matrix multiplication, elements in the result matrix are obtained by taking the sums of the products of the elements of a row of the first with a column of the second • Calculating the sum of products of the ith row with the jth column produces the element at location [i][j]

Matrix Multiplication

Matrix Multiplication • In order to calculate a sum of products, the length of a row of the first matrix must be equal to the length of a column 3 columns in the second matrix • length of a row = # columns • length of a column = # rows 3 rows row column

Matrix Multiplication • Can therefore only multiply m x k matrix with a k x n matrix • # of columns of first operand = # rows of second operand • Results in an m x n matrix 3 rows 2 rows 3 rows 2 columns 4 columns

An Example

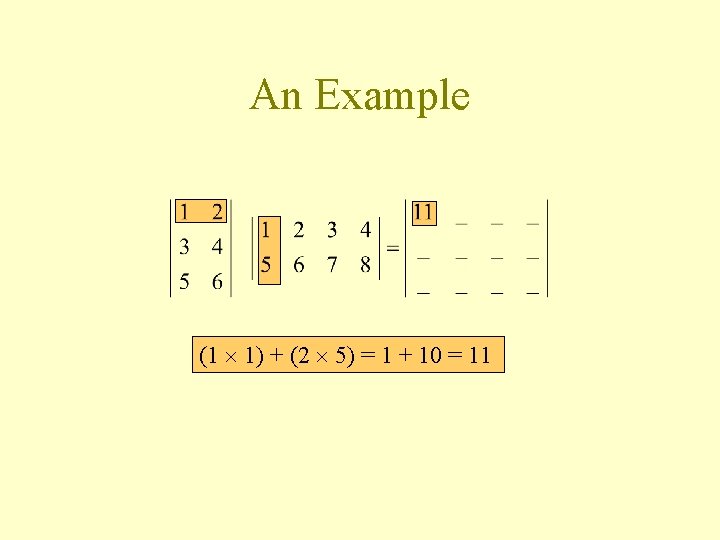
An Example (1 1) + (2 5) = 1 + 10 = 11

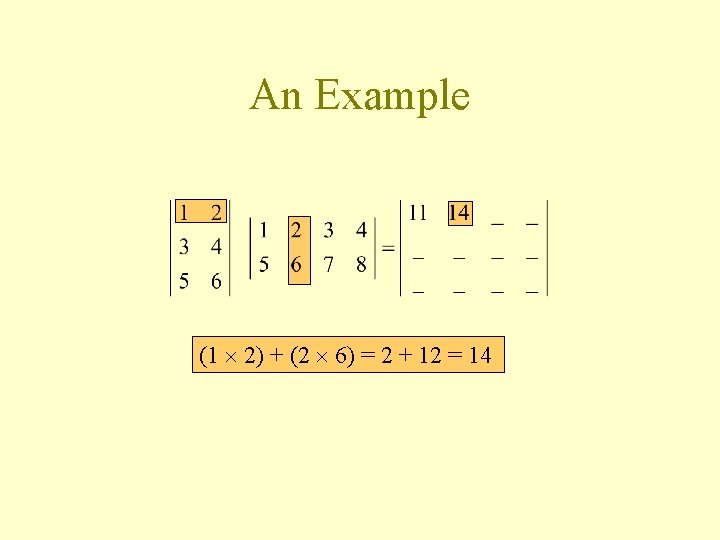
An Example (1 2) + (2 6) = 2 + 12 = 14

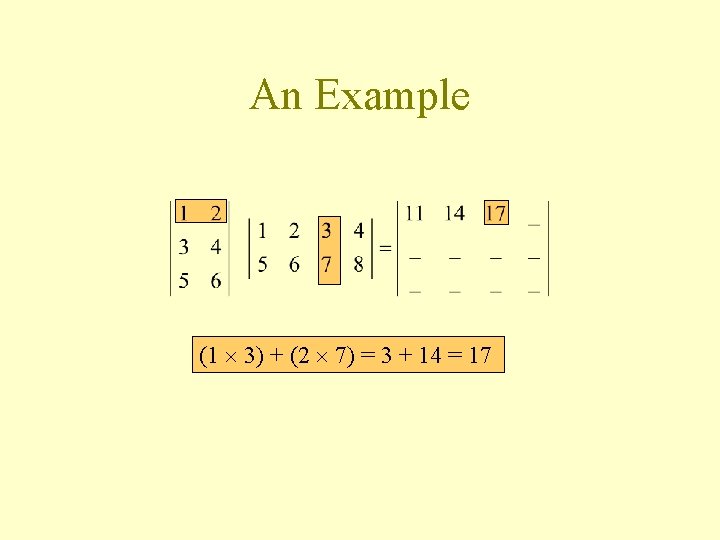
An Example (1 3) + (2 7) = 3 + 14 = 17

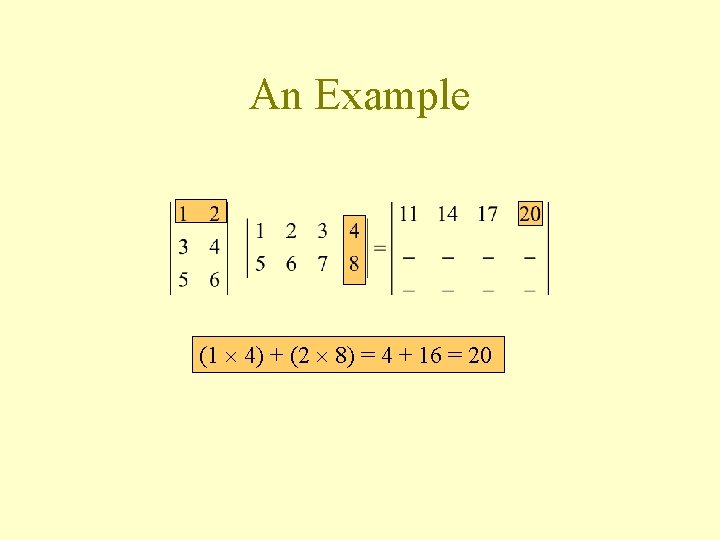
An Example (1 4) + (2 8) = 4 + 16 = 20

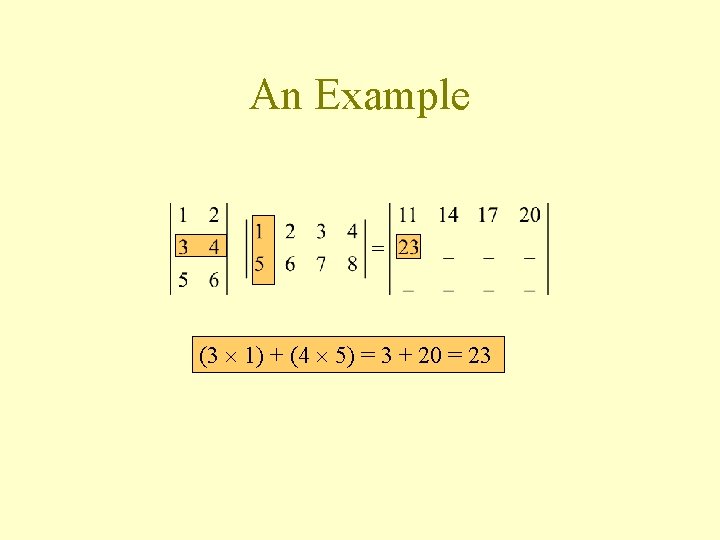
An Example (3 1) + (4 5) = 3 + 20 = 23

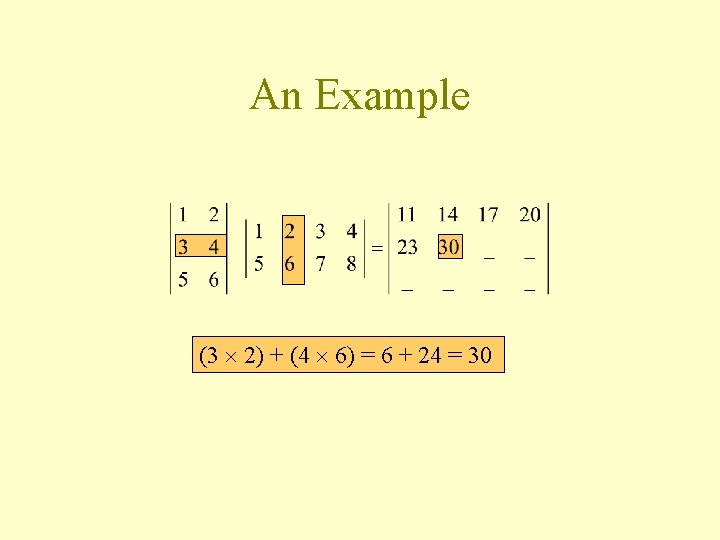
An Example (3 2) + (4 6) = 6 + 24 = 30

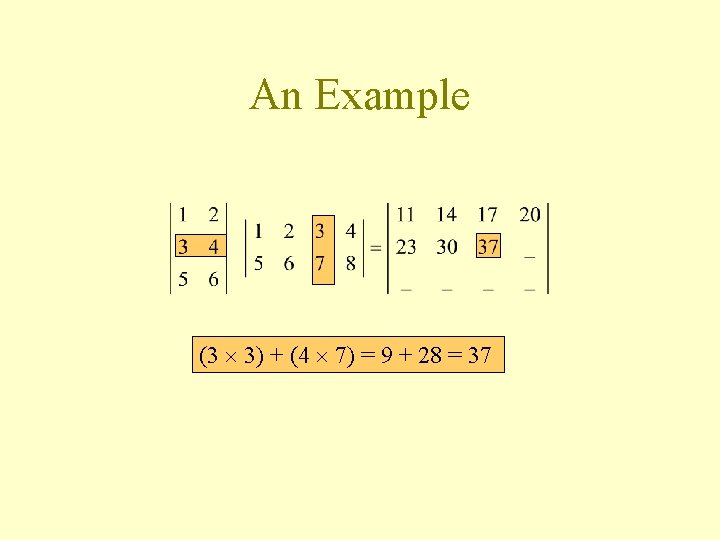
An Example (3 3) + (4 7) = 9 + 28 = 37

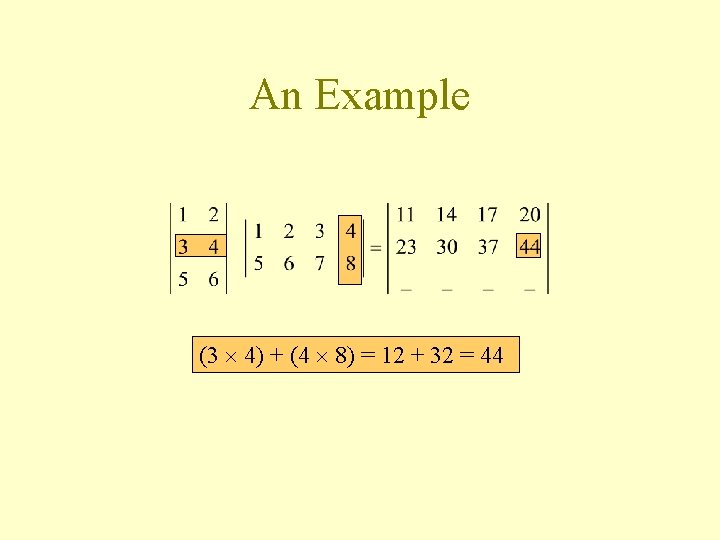
An Example (3 4) + (4 8) = 12 + 32 = 44

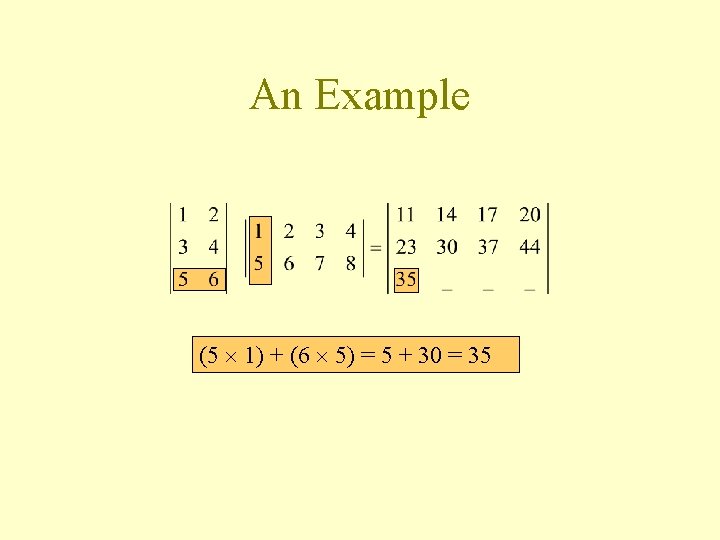
An Example (5 1) + (6 5) = 5 + 30 = 35

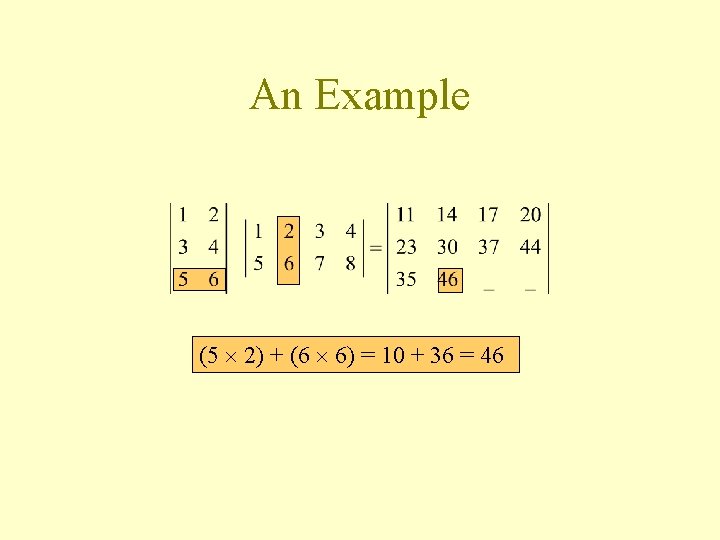
An Example (5 2) + (6 6) = 10 + 36 = 46

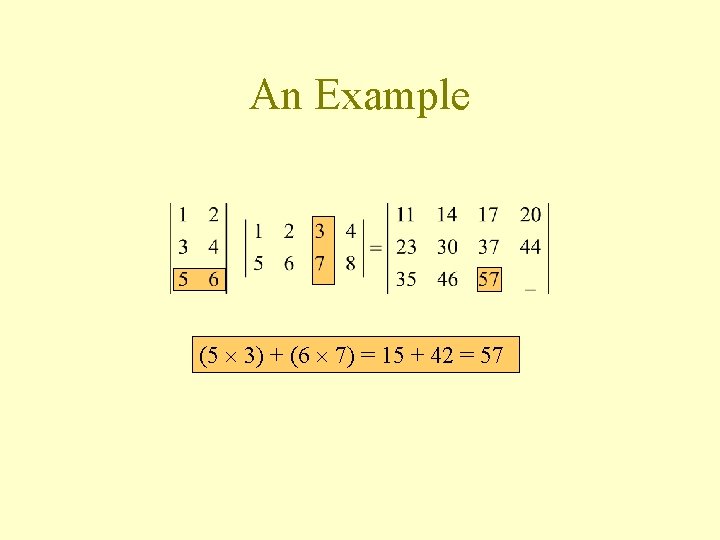
An Example (5 3) + (6 7) = 15 + 42 = 57

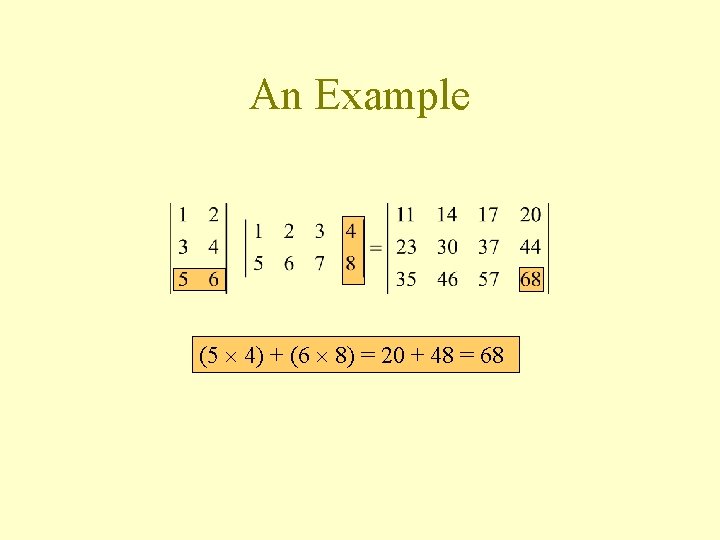
An Example (5 4) + (6 8) = 20 + 48 = 68

The Algorithm multiply(a, b) // a = M x K b = K x N result = new Matrix(m, n) for i = 1, M // M rows in a for j = 1, N // N columns in b result[i][j] = 0 for k = 1, K // K columns in a, rows in b result[i][j] += a[i, k] * b[k, j] return result

What’s this got to do with us? • Matrices are a convenient and powerful way of expressing transformations • Allows complex sequences of complex transformations to be easily expressed and calculated • Let’s look at one simple transformation and see how

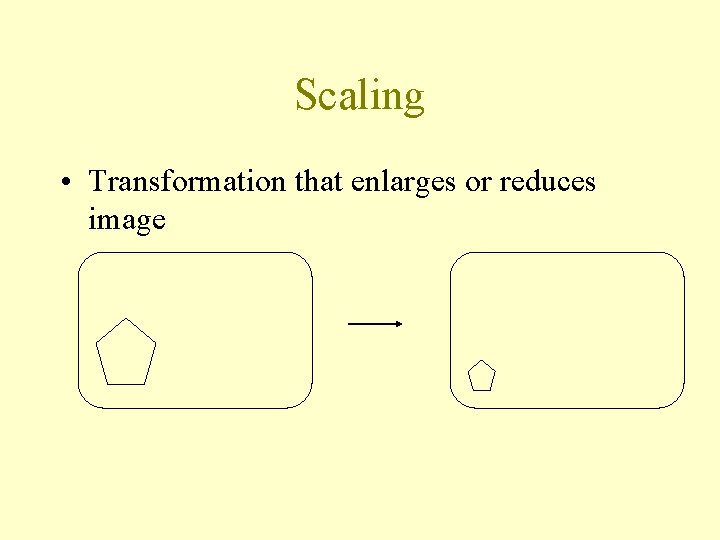
Scaling • Transformation that enlarges or reduces image

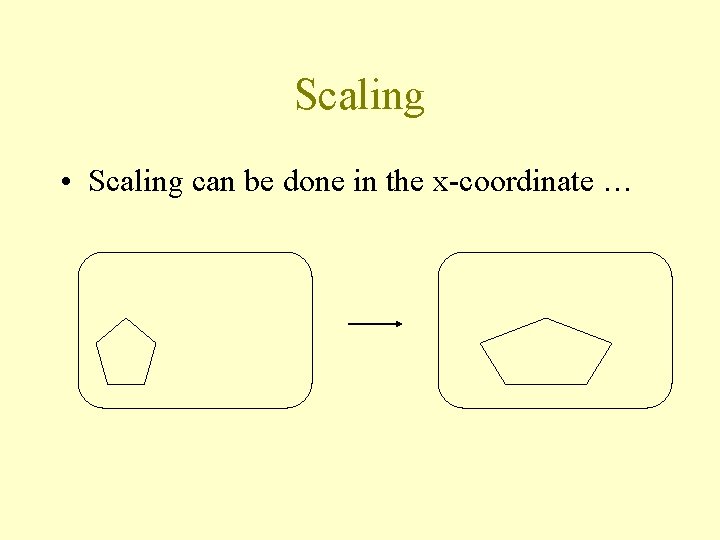
Scaling • Scaling can be done in the x-coordinate …

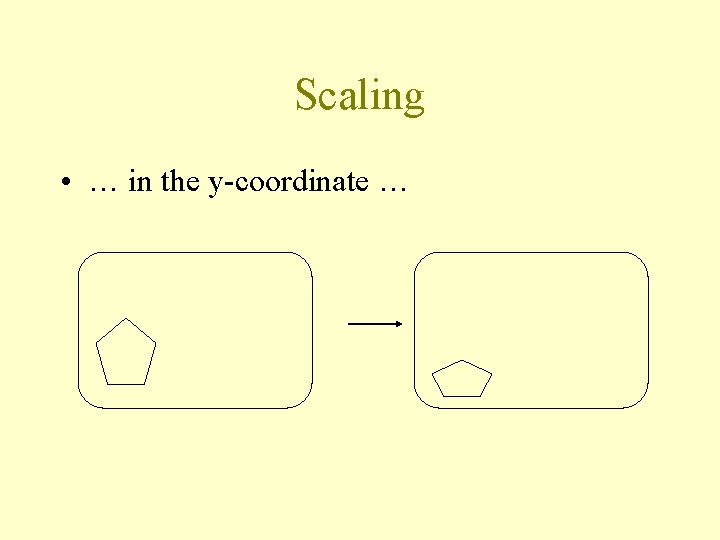
Scaling • … in the y-coordinate …

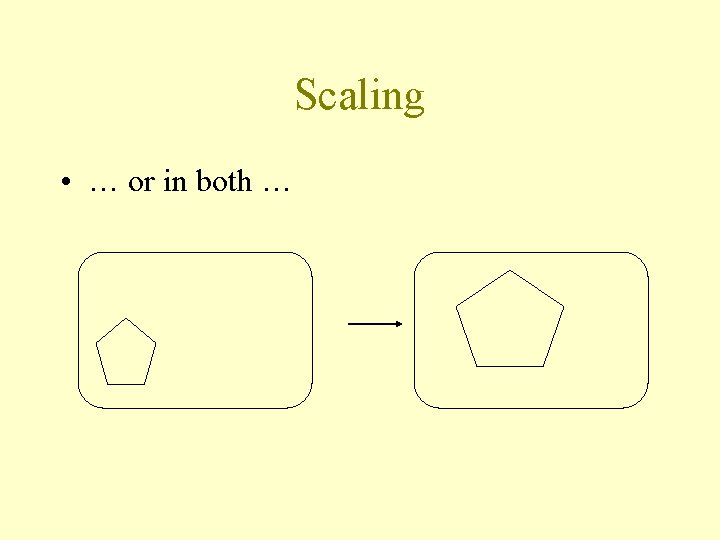
Scaling • … or in both …

Scaling • We could simply say that • To scale in the x-coordinate, multiply by the scaling factor • that is, to scale to double the size in the xcoordinate, simply multiply the x-coordinate of all endpoints by 2 • Similarly to reduce the size • Similarly in the y-direction

Simple enough • The above works and is totally adequate to scale • Why complicate matters? • Why even consider doing anything else?

Multiple Transformations • Will want to • scale and rotate • translate, rotate and translate again • etc, … • Don’t want to have to apply each transformation individually

Using Matrices • Let’s represent a point as a 1 x 2 matrix • We often call a 1 x n matrix a vector • Let’s reexamine multiplying this vector with a 2 x 2 matrix

Applying Matrix Multiplication • We can think of the above multiplication taking the point (x, y) and producing a new point (x', y') where • x' = ax + cy • y' = bx + dy

Transformation Matrix • We see that when a 2 x 2 matrix • is multiplied with a 1 x 2 vector representing a point … • … a new 1 x 2 vector is produced … • … that can be though of as representing a new point • We thus call the 2 x 2 matrix a transformation matrix • The matrix when applied to the original point transforms it into the new point

Where Matrix Multiplication Comes In x' y' • Looking at the above we can get a sense of how the 2 x 2 matrix transforms the point: a: the effect of the original xvalue on the new x-value c: the effect of the original yvalue on the new x-value b: the effect of the original xvalue on the new y-value d: the effect of the original yvalue on the new y-value

An Trivial Example • Following this line of thought, the matrix: a: the original x-value has an identity effect on the new xvalue c: the original y-value has no effect on new x-value b: the original x-value has no effect on the new y-value d: the original y-value has an identity effect on the new yvalue should transform the original point back to itself

A Trivial Example • To see that this is so: • The matrix is called the identity matrix

Applying this to Scaling • Using this approach, let’s try to produce some transformation matrices for scaling • Let’s first scale the x-coordinate alone • We’d like • the new (transformed) x-value • to be a factor of the original x-value • not be affected by the original y-value • the new (transformed) y-value • to be identical to the original x-value • (not be affected by the original x-value)

Doubling the Size in the x-Direction • As an example, to double the x-value • We’d like • the new (transformed) x-value • to be 2 times the original x-value • not be affected by the original y-value • the new (transformed) y-value • to be identical to the original x-value • (not be affected by the original x-value)

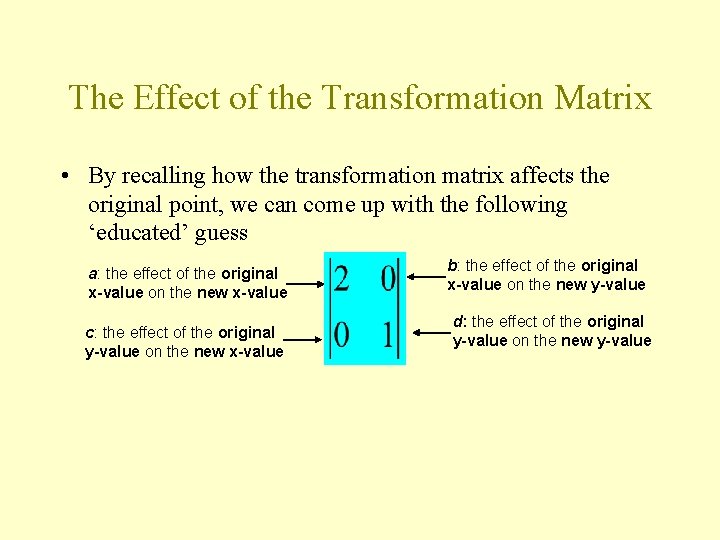
The Effect of the Transformation Matrix • By recalling how the transformation matrix affects the original point, we can come up with the following ‘educated’ guess a: the effect of the original x-value on the new x-value c: the effect of the original y-value on the new x-value b: the effect of the original x-value on the new y-value d: the effect of the original y-value on the new y-value

Checking Our Guess • Doing the multiplication produces • So we see indeed, our hunch was correct!

Other Scaling Matrices • The same line of reasoning produces • The general transformation matrix for scaling in the xdirection alone • The general transformation matrix for scaling in the ydirection alone • The general transformation matrix for scaling in both directions For practice, verify these by doing the matrix multiplications!!

Applying Multiple Transformations • If we multiply the ‘scale x’ matrix and the ‘scale y’ matrix, we obtain the scale matrix for both

Applying Multiple Transformations • Similarly, if we multiply the ‘double size’ matrix and the ‘half size’ matrix, we obtain the identity matrix

Applying Multiple Transformations • Although we won’t prove it, it can be shown that multiplying two transformation matrices produces a transformation matrix whose effect is the first transformation followed by the second! • This result extends to three or more as well

Applying Multiple Transformations • This is a valuable result because it means we can achieve the effect of several transformation by applying a single matrix to our image rather than having to perform a sequence of transforms.

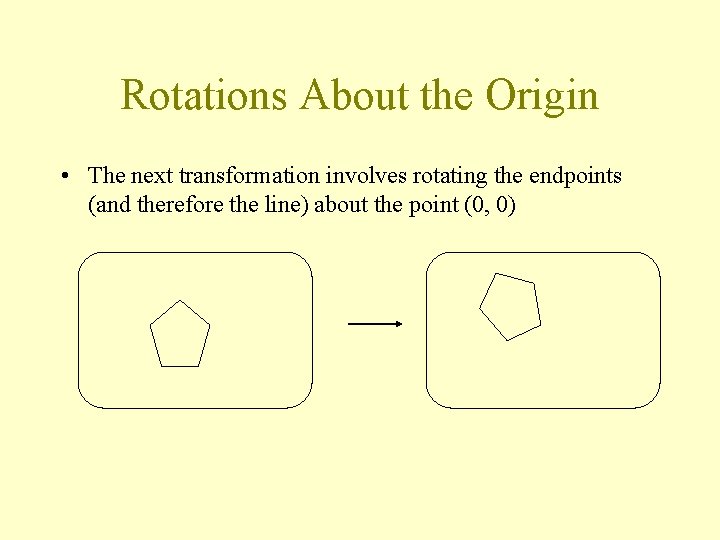
Rotations About the Origin • The next transformation involves rotating the endpoints (and therefore the line) about the point (0, 0)

Rotations About the Origin • Again, we will try to derive the transformation matrix • This one is a bit more involved and requires some trigonometry and geometry

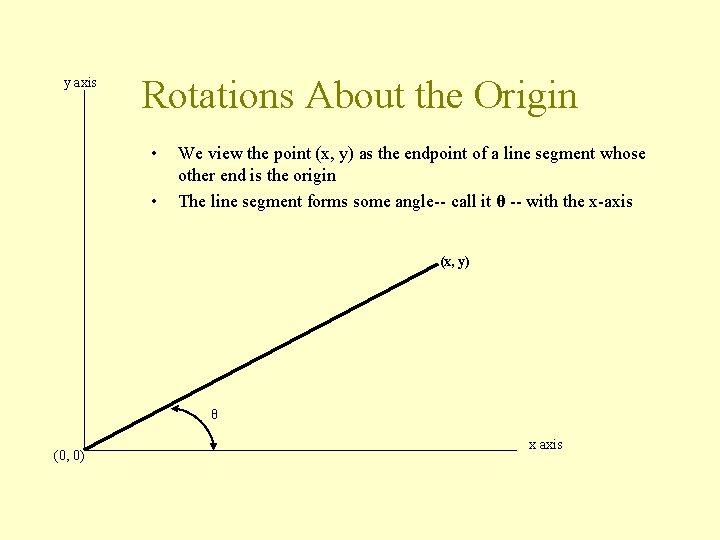
y axis Rotations About the Origin • • We view the point (x, y) as the endpoint of a line segment whose other end is the origin The line segment forms some angle-- call it θ -- with the x-axis (x, y) θ (0, 0) x axis

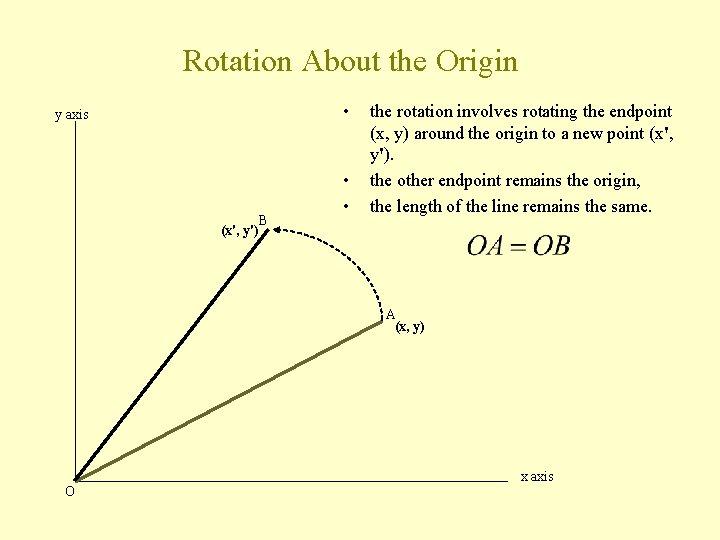
Rotation About the Origin • y axis (x', y') B • • the rotation involves rotating the endpoint (x, y) around the origin to a new point (x', y'). the other endpoint remains the origin, the length of the line remains the same. A (x, y) O x axis

Rotation About the Origin • We’d like to define the value of the new (transformed) point (x', y') in terms of the original point(x, y) • If we can do that, we can come up with a transformation matrix! • And, again, as we said before, this will require a bit of math

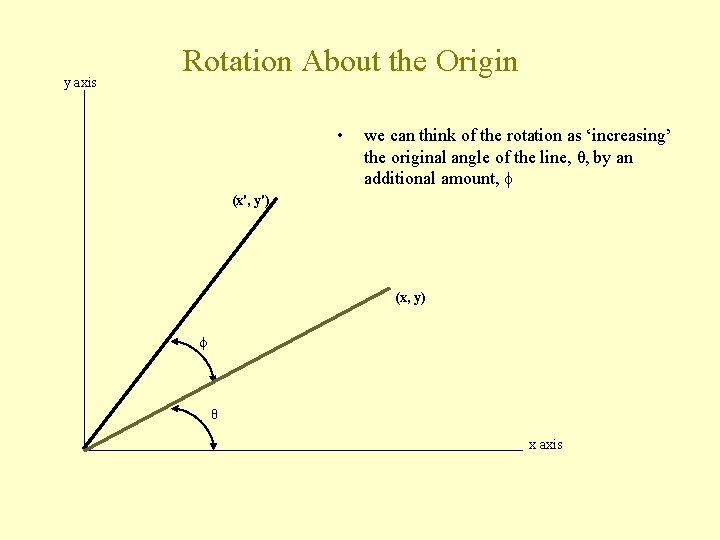
y axis Rotation About the Origin • we can think of the rotation as ‘increasing’ the original angle of the line, θ, by an additional amount, (x', y') (x, y) θ x axis

The Sum of Two Angles • Given two angles and : sin( + ) = cos sin + sin cos( + ) = cos - sin • We’re not going to derive these formulae

Remember SOHCAHTOA? • For right triangles θ • sine = opposite / hypotenuse • cosine = opposite / hypotenuse θ θ • tangent = opposite / adjacent (we won’t be using this)

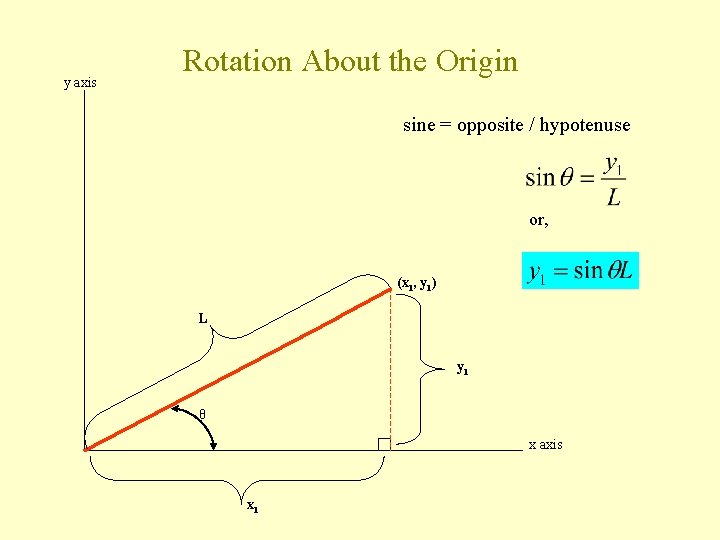
y axis Rotation About the Origin sine = opposite / hypotenuse or, (x 1, y 1) L y 1 θ x axis x 1

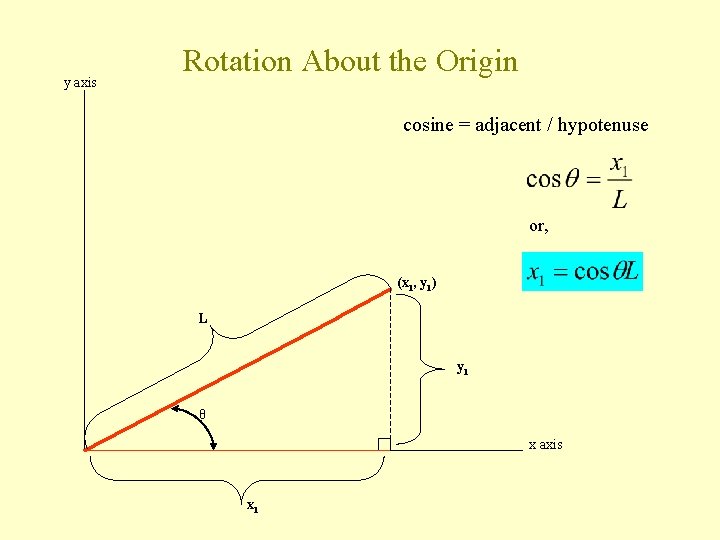
y axis Rotation About the Origin cosine = adjacent / hypotenuse or, (x 1, y 1) L y 1 θ x axis x 1

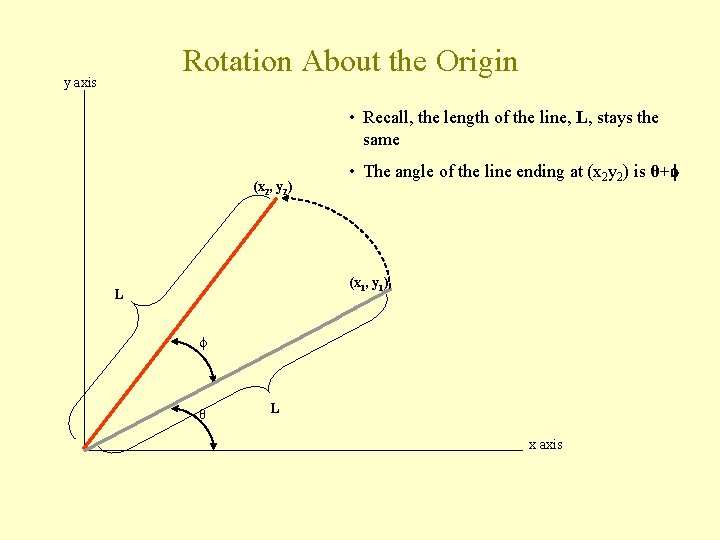
Rotation About the Origin y axis • Recall, the length of the line, L, stays the same (x 2, y 2) • The angle of the line ending at (x 2 y 2) is θ+ (x 1, y 1) L θ L x axis

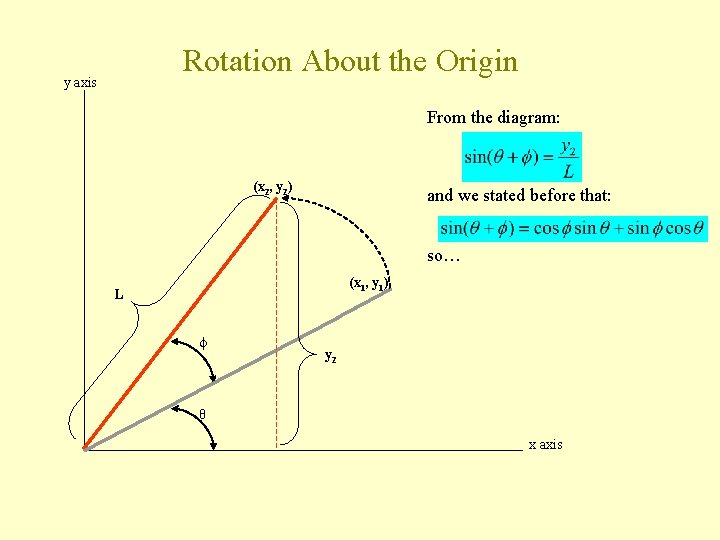
Rotation About the Origin y axis From the diagram: (x 2, y 2) and we stated before that: so… (x 1, y 1) L y 2 θ x axis

Through the Magic of Algebraic Manipulation And since We get We have defined y 2 in terms of x 1 and y 1– exactly what we were looking for!!!

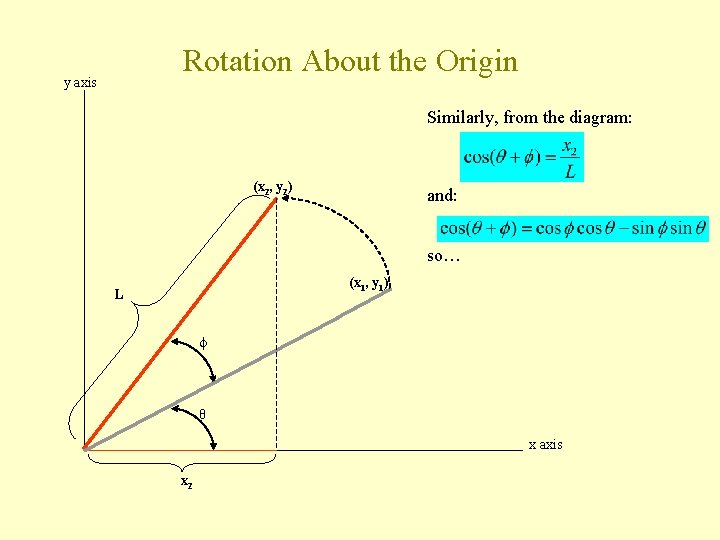
Rotation About the Origin y axis Similarly, from the diagram: (x 2, y 2) and: so… (x 1, y 1) L θ x axis x 2

More Magic of Algebraic Manipulation And again, since We get We have similarly defined x 2 in terms of x 1 and y 1– again exactly what we were looking for!!!

A Rotation-Around-the-Origin Matrix • Given and we can clearly see the effects of x 1 and y 1 on x 2 and y 2 • • x 1 affects x 2 via cos x 1 affects y 2 via sin y 1 affects x 2 via -sin y 1 affects y 2 via cos

A Rotation Around the Origin Matrix • This results in the transformation matrix for a rotation about the origin of angle the effect of the original xvalue on the new x-value the effect of the original yvalue on the new x-value the effect of the original xvalue on the new y-value the effect of the original yvalue on the new y-value

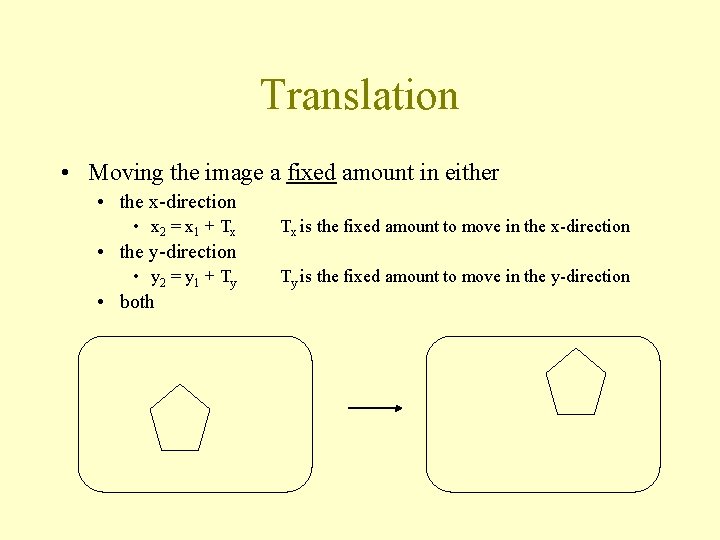
Translation • Moving the image a fixed amount in either • the x-direction • x 2 = x 1 + Tx Tx is the fixed amount to move in the x-direction • the y-direction • y 2 = y 1 + Ty • both Ty is the fixed amount to move in the y-direction

Translation • Sounds easy • add the x translation amount to the x coordinate • add the y translation amount to the y coordinate • But we’d like to have a matrix • Would like to combine our various transformations • OTOH, is that really all that important?

Rotation About an Arbitrary Point • We’d like to rotate around points other than the origin

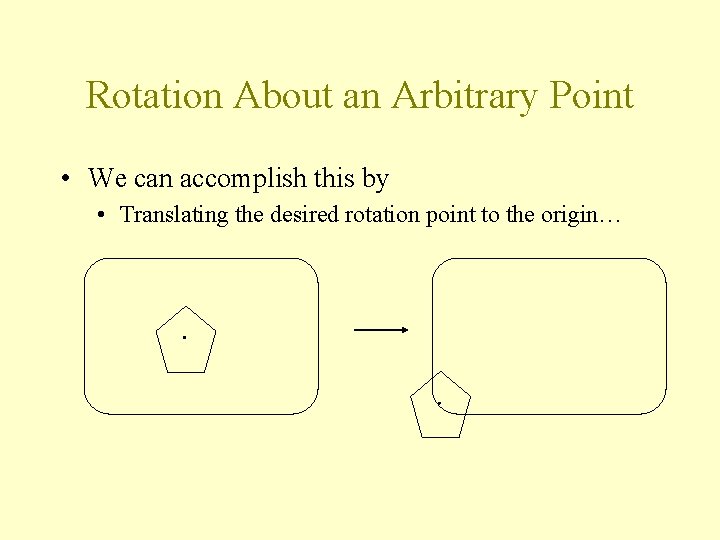
Rotation About an Arbitrary Point • We can accomplish this by • Translating the desired rotation point to the origin…

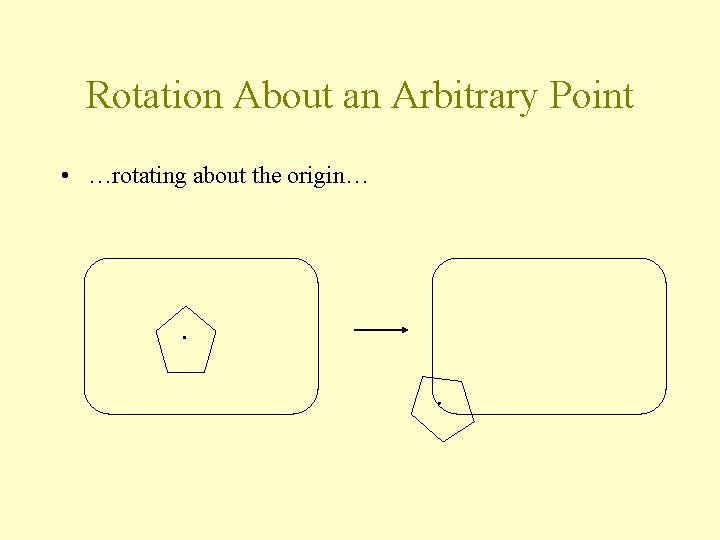
Rotation About an Arbitrary Point • …rotating about the origin…

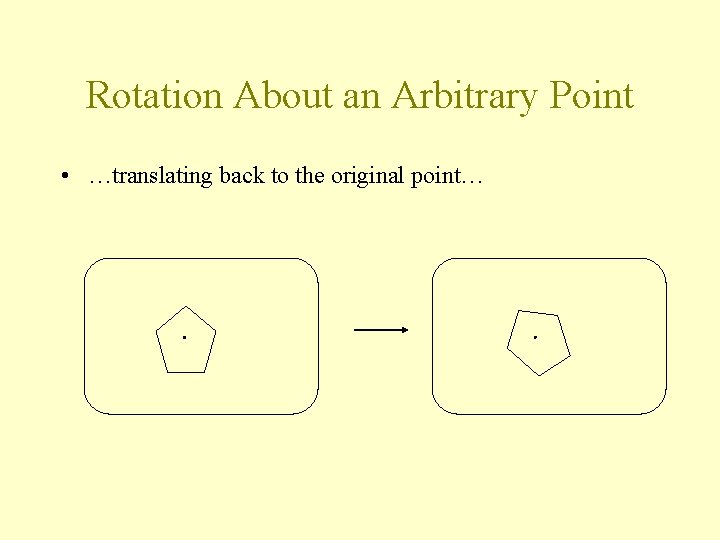
Rotation About an Arbitrary Point • …translating back to the original point…

The Problem • Our transformation matrices till now had entries for • How the old x affects the new x and y • How the old y affects the new x and y a: the effect of the original xvalue on the new x-value c: the effect of the original yvalue on the new x-value b: the effect of the original xvalue on the new y-value d: the effect of the original yvalue on the new y-value

The Problem • In a translation, the changes are fixed • independent of the original x and y values • Where would they go in the matrix?

Homogeneous Coordinates • An approach to incorporating a fixed translation into a transformation matrix • Using homogeneous coordinates involves…

Homogeneous Coordinates • Using a 3 x 3 transformation matrix rather than a 2 x 2… • For example, our scaling matrix becomes • Not too bad– the extra row/column looks like an identity matrix • The 0’s and 1 shouldn’t make the sums of products much harder to do • Similarly for the rotation matrix

Homogeneous Coordinates • The introduction of an additional ‘dummy’ coordinate, w • Points are now specified by a 1 x 3 vector • We can always get x and y back again by dividing by w • And in any event, don’t get too worried, we’re going to keep w = 1

Homogeneous Coordinates • Let’s just see the effect of all this • As an example, we’ll do a scaling • Which is the correct representation under homogeneous coordinates for the new (scaled) point • … And similarly for rotation • You can do the math if you want

A Translation Matrix • Let’s try to understand this matrix • The original x and y have an identity effect (the shaded 2 x 2 matrix is the identity matrix) on the new points • The Tx and Ty will be multiplied by w (if you can’t visualize this, you’ll see it on the next slide) and added into the sum of products • Dividing the result by w would then produce the fixed translation value • To see this, let’s do the math

A Translation Matrix • And again, this is the desired point • modulo the division by w

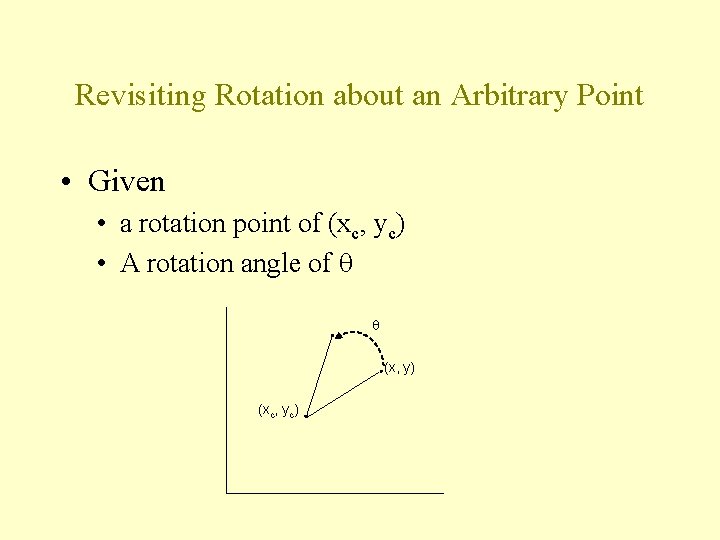
Revisiting Rotation about an Arbitrary Point • Given • a rotation point of (xc, yc) • A rotation angle of (x, y) (xc, yc)

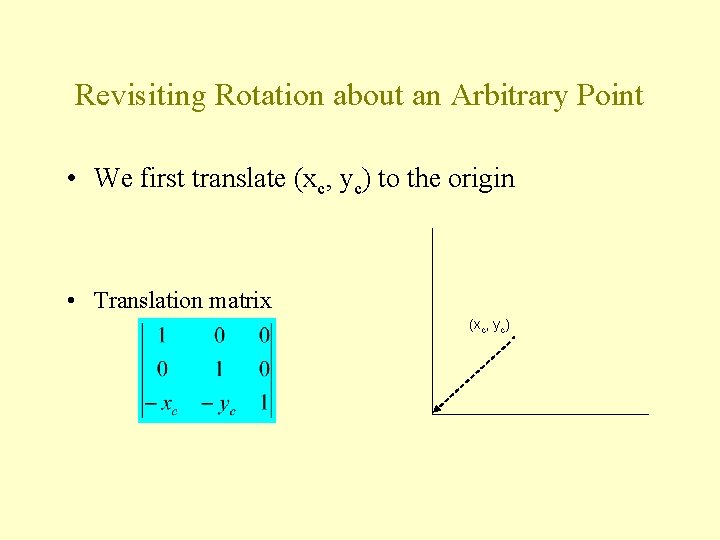
Revisiting Rotation about an Arbitrary Point • We first translate (xc, yc) to the origin • Translation matrix (xc, yc)

Revisiting Rotation about an Arbitrary Point • We then perform the rotation (around the origin) of angle … • Rotation matrix

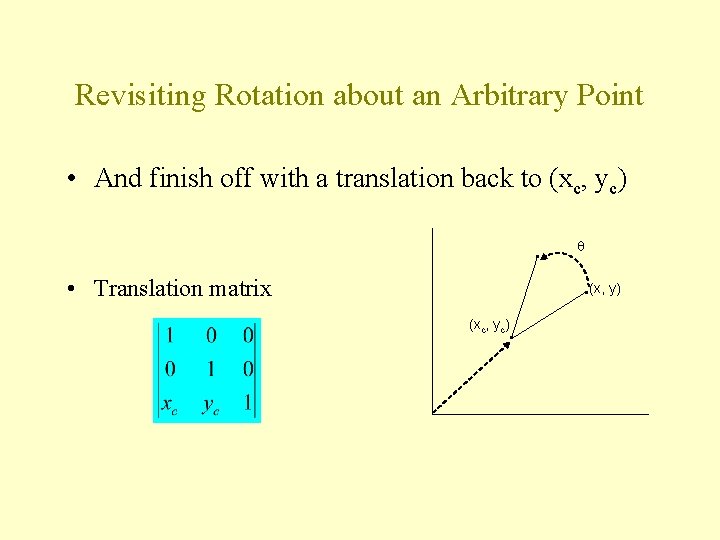
Revisiting Rotation about an Arbitrary Point • And finish off with a translation back to (xc, yc) • Translation matrix (x, y) (xc, yc)

A Matrix for Rotation about an Arbitrary Point • Putting it all together, gives us and performing the multiplications produces