Transformations of the Graphs of Sine and Cosine

Transformations of the Graphs of Sine and Cosine Functions Credit to: JMerrill, 2010 EQ: How do I transform the graphs of trigonometric functions?

Objective: Students will be able to transform sine and cosine functions. Translations of General Sine Waves • Referring to our previous equations y = a sin bx y = a cos bx What does a refer to? What does b refer to? • If we translate the graphs h units horizontally, and k units vertically, then the resulting equations are: y = a sin b(x – c) + d y = a cos b(x – c) + d

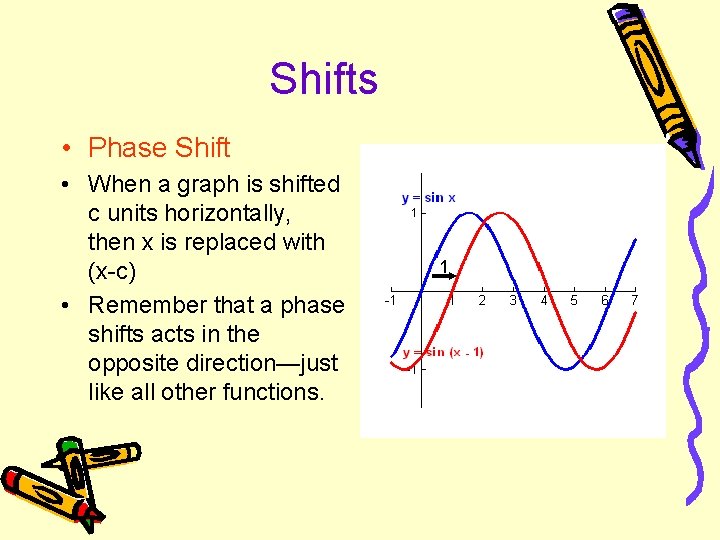
Shifts • Phase Shift • When a graph is shifted c units horizontally, then x is replaced with (x-c) • Remember that a phase shifts acts in the opposite direction—just like all other functions. 1

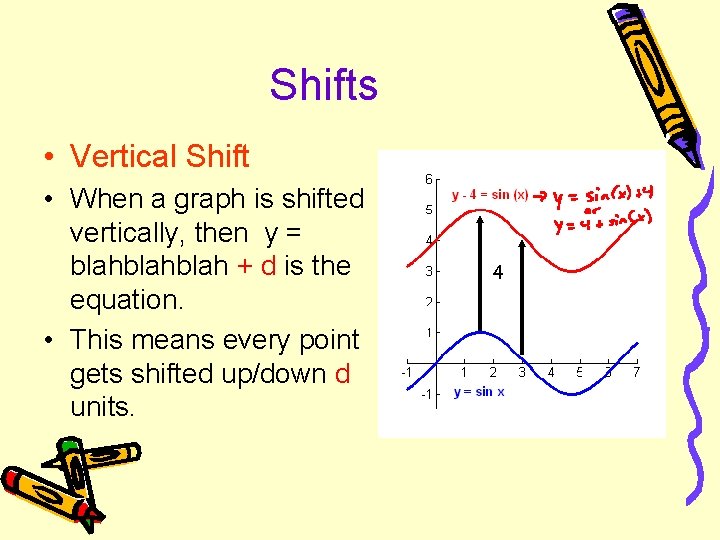
Shifts • Vertical Shift • When a graph is shifted vertically, then y = blahblah + d is the equation. • This means every point gets shifted up/down d units. 4

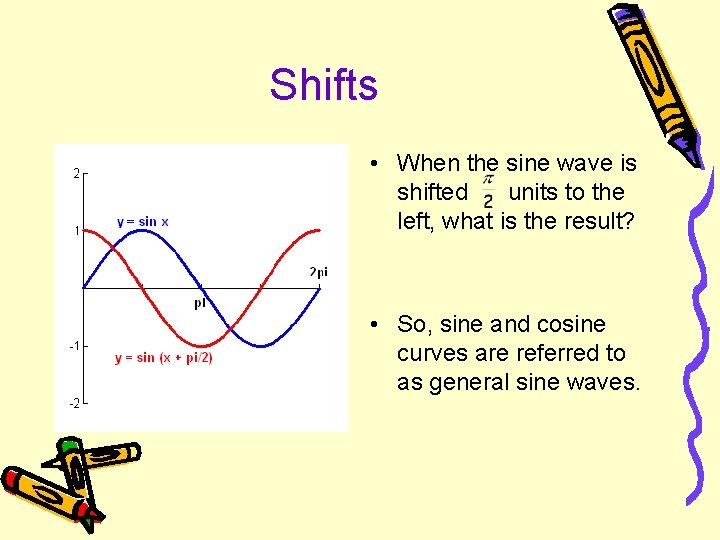
Shifts • When the sine wave is shifted units to the left, what is the result? • So, sine and cosine curves are referred to as general sine waves.

Axis of the Wave (Vertical Translation) • If the x-axis is not the center of the wave, then you need to find the center. The center is the average of the peak and the valley points • Axis of the wave: y =

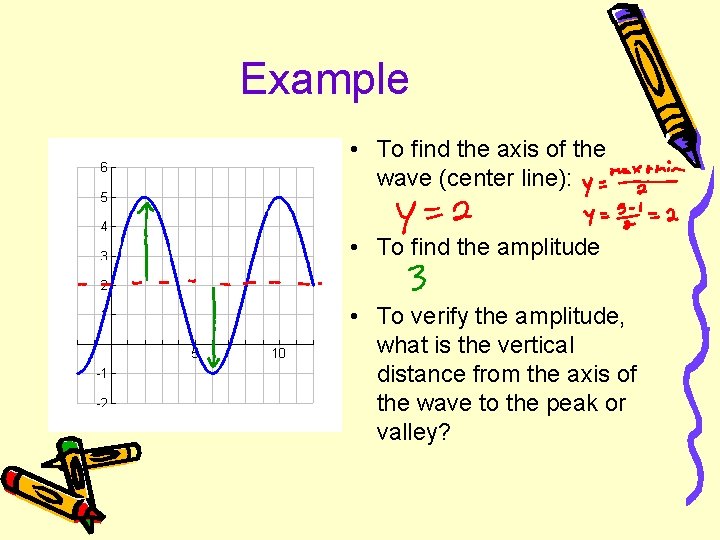
Example • To find the axis of the wave (center line): • To find the amplitude • To verify the amplitude, what is the vertical distance from the axis of the wave to the peak or valley?

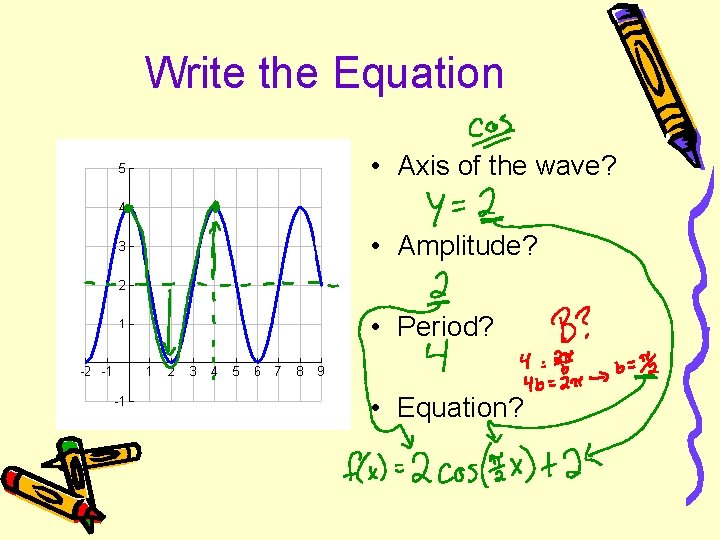
Write the Equation • Axis of the wave? • Amplitude? • Period? • Equation?

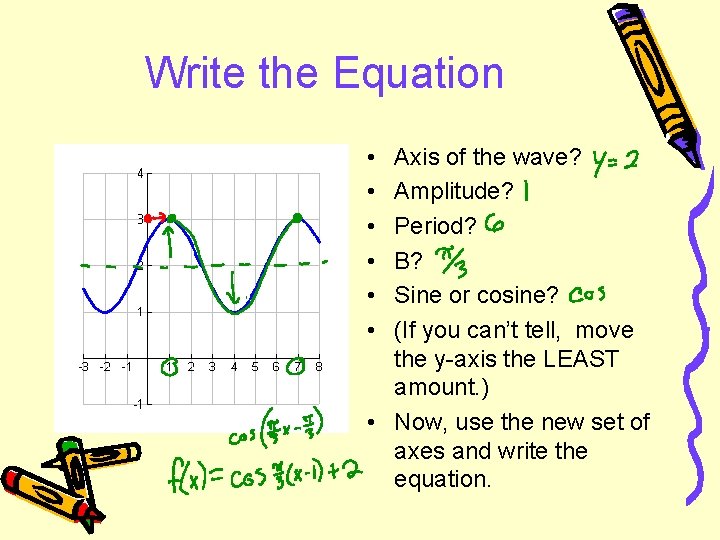
Write the Equation • • • Axis of the wave? Amplitude? Period? B? Sine or cosine? (If you can’t tell, move the y-axis the LEAST amount. ) • Now, use the new set of axes and write the equation.

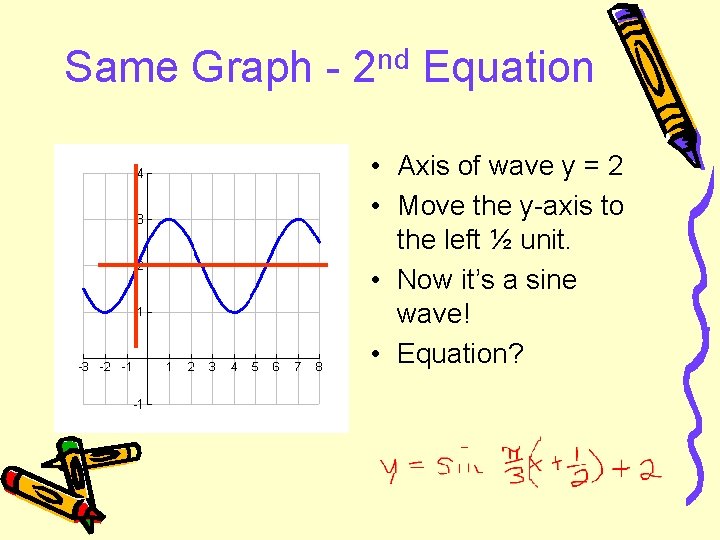
Same Graph - 2 nd Equation • Axis of wave y = 2 • Move the y-axis to the left ½ unit. • Now it’s a sine wave! • Equation?

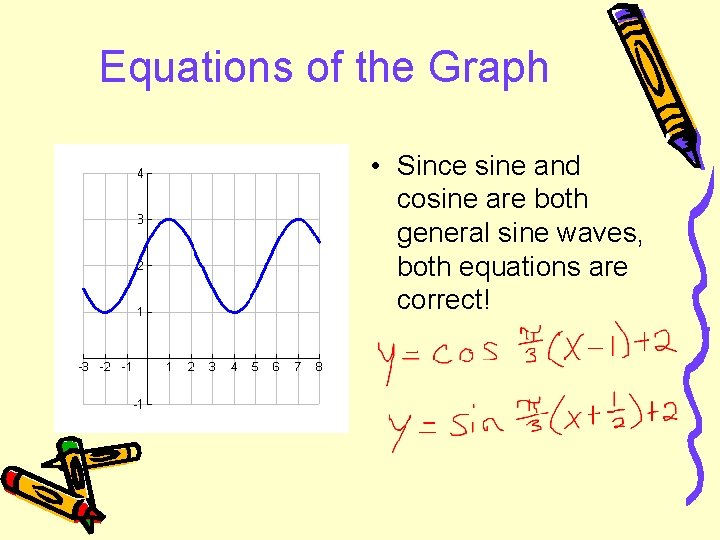
Equations of the Graph • Since sine and cosine are both general sine waves, both equations are correct!

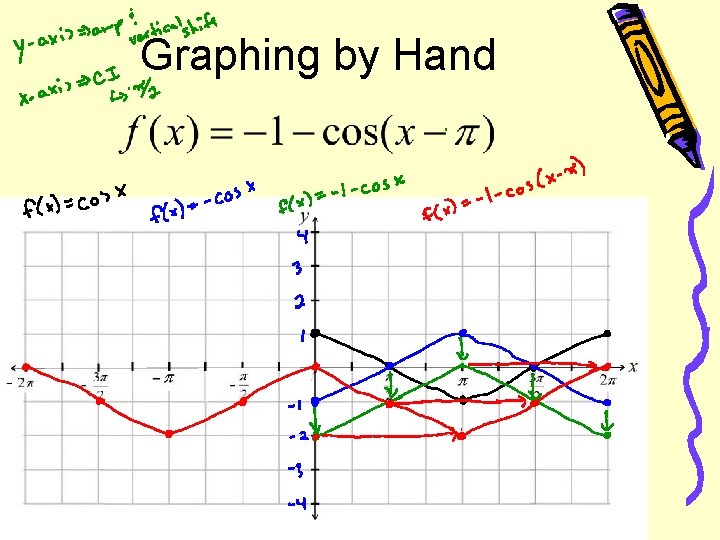
Graphing by Hand

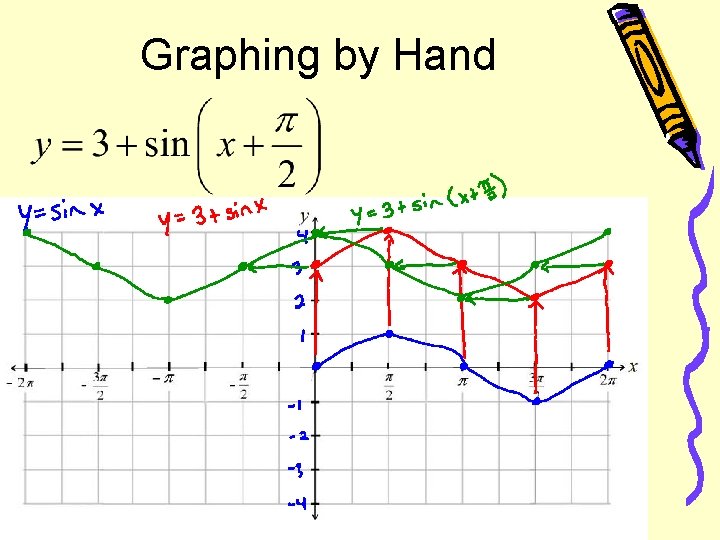
Graphing by Hand

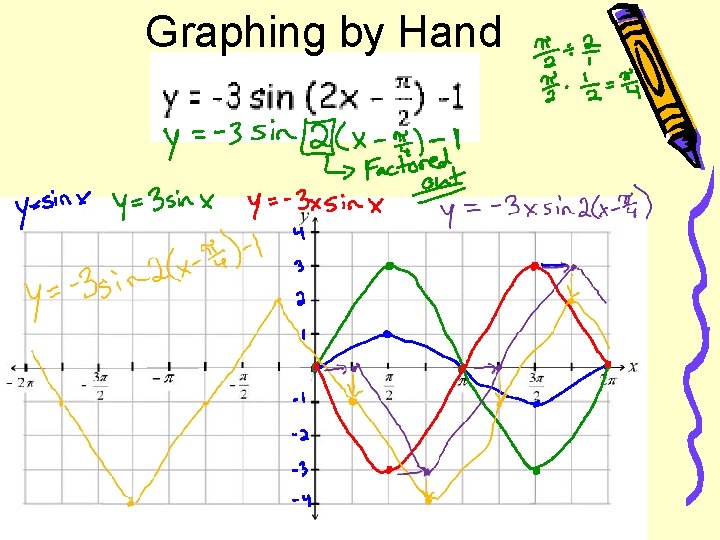
Graphing by Hand