TRANSFORMATIONS OF LINEAR QUADRATIC ABSOLUTE VALUE GRAPHS Algebra

TRANSFORMATIONS OF LINEAR, QUADRATIC, & ABSOLUTE VALUE GRAPHS Algebra II Guram Dr.

Focus Questions � How do we draw transformations of linear, quadratic, and absolute value graphs? � Can we utilize a real-world scenario where transformations occur?

Curriculum standards HSF-BF. B. 3 Identify the effect on the graph of replacing f(x) by f(x) + k, kf(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. � HSF-IF. C. 7 Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases. � HSF-IF. C. 7 b Graph piecewise-defined functions, including step functions and absolute value functions. � Sources: http: //www. corestandards. org/Math/Content/HSA/CED/A/1/ � Spring Board Algebra 2 Textbook �

Real World Examples Utilizing Transformations � What are examples of ways people utilize transformations in real world situations? ? ? ?

Real World Examples Utilizing Transformations - - - Speed of objects (boat speed) Questions involving populations Science (Physiology)

Academic language � Transformation: A transformation changes a graph’s size, shape, position, or orientation.

Graphing Quadratic Equations Vertex Form: Vertex: (h, k) Direction: a Steps: 1. You must set bx – h = 0 and solve for x. This will give you h. 2. Make a T-Table and choose points to the right and left of h. 3. If you have a fraction in the problem choose points that eliminate the fraction. 4. You may chose to remove the shift(h, k) and select x-values to move to the next point.

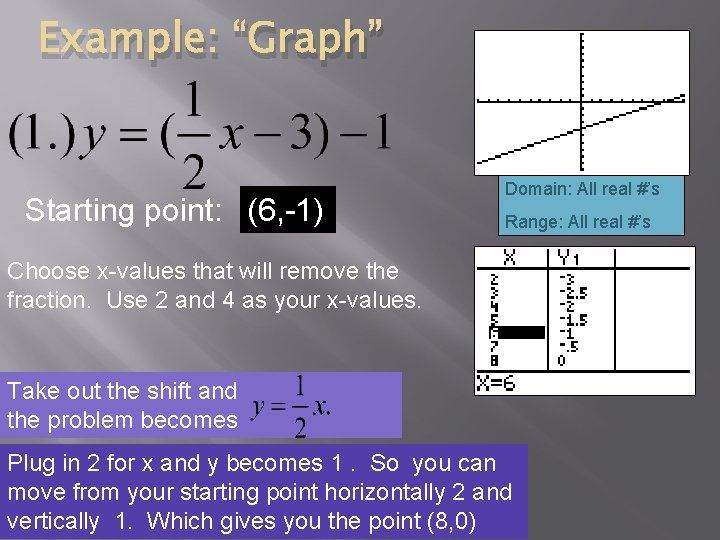
Example: “Graph” Starting point: (6, -1) Domain: All real #’s Range: All real #’s Choose x-values that will remove the fraction. Use 2 and 4 as your x-values. Take out the shift and the problem becomes Plug in 2 for x and y becomes 1. So you can move from your starting point horizontally 2 and vertically 1. Which gives you the point (8, 0)

Vertex: (2, 1) Direction: (a=1) Up Choose x-values to the right and left of 2. Use 1 and 3 as your x-values. Take out the shift and the problem becomes Domain: All real #’s Range: All real #’s Plug in 1 for x and y becomes 4. So you can move from your vertex horizontally 1 and vertically 4. Which gives you the point (3, 5). 1.

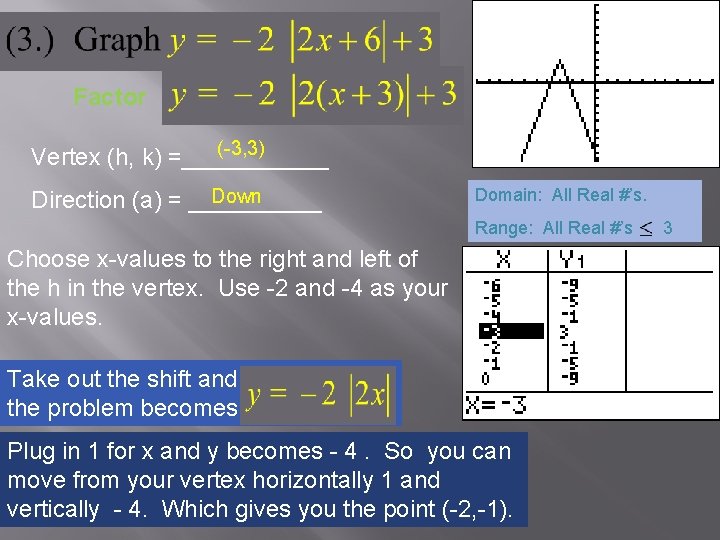
Factor (-3, 3) Vertex (h, k) =______ Down Direction (a) = _____ Domain: All Real #’s. Range: All Real #’s Choose x-values to the right and left of the h in the vertex. Use -2 and -4 as your x-values. Take out the shift and the problem becomes Plug in 1 for x and y becomes - 4. So you can move from your vertex horizontally 1 and vertically - 4. Which gives you the point (-2, -1). 3

Review � How do we draw transformations of linear, quadratic, and absolute value graphs? � Can we utilize a real-world scenario where transformations occur?

Review of terms � Explain the mathematical term: transformation. � Define the mathematical term: translation, domain, and range.

Classwork/Homework - Transformation Worksheet