Transformations Infinity and Graphing By Laura Hannah Ana

Transformations, Infinity, and Graphing By: Laura, Hannah, Ana, Drew M. , and Robyn 4 th Period

Infinity Limits and Limits at Infinity… There are two kinds of limits involving the idea of infinity… 1) Where the limit DNE or is +/- infinity 2) Where there is a limit as the value approaches +/- infinity Type 1 Example: Note: If the � problem does not specify a right or left hand limit, you must check both to make sure they equal each other.

Type 2 Example and Shortcuts • Our friend Patrick will show us an example of how to solve a limit problem at infinity without the use of shortcuts • The important component for limits at infinity (with rational polynomials) is to divide by the HIGHEST POWER • However, there a few shortcuts… 1) Degree of Numerator=Degree of Denominator Limit (as x approaches infinity) = Ratio of Leading Coefficients of Highest Degree 2) Degree of Numerator<Degree of Denominator Limit (as x approaches infinity)= 3) Degree of Numerator>Degree of Denominator Limit (as x approaches infinity)=

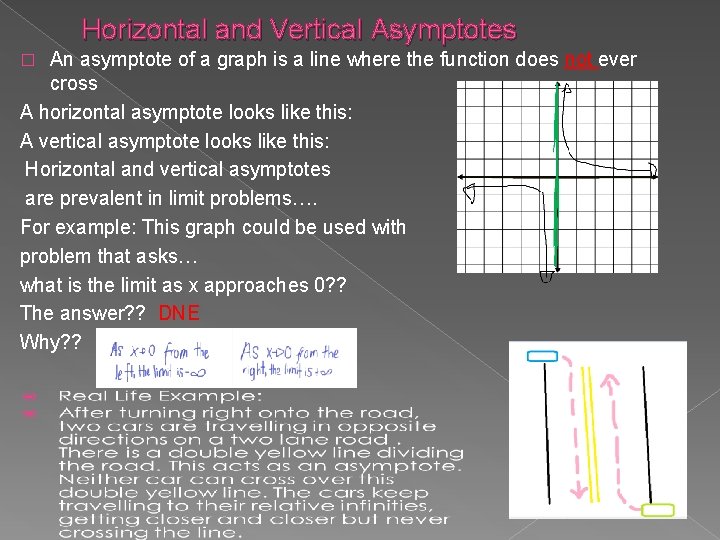
Horizontal and Vertical Asymptotes An asymptote of a graph is a line where the function does not ever cross A horizontal asymptote looks like this: A vertical asymptote looks like this: Horizontal and vertical asymptotes are prevalent in limit problems…. For example: This graph could be used with problem that asks… what is the limit as x approaches 0? ? The answer? ? DNE Why? ? �

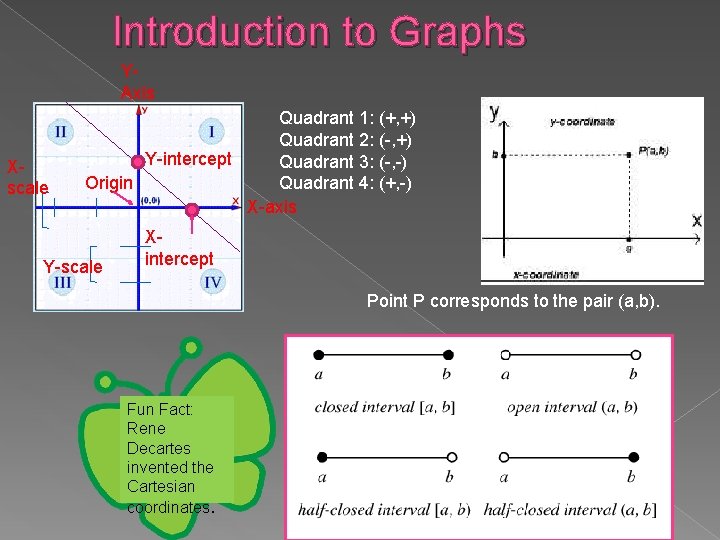
Introduction to Graphs YAxis Xscale -2 Quadrant 1: (+, +) Quadrant 2: (-, +) Y-intercept Quadrant 3: (-, -) Origin Quadrant 4: (+, -) X-axis -1 -1 Y-scale Xintercept -2 Point P corresponds to the pair (a, b). Fun Fact: Rene Decartes invented the Cartesian coordinates.

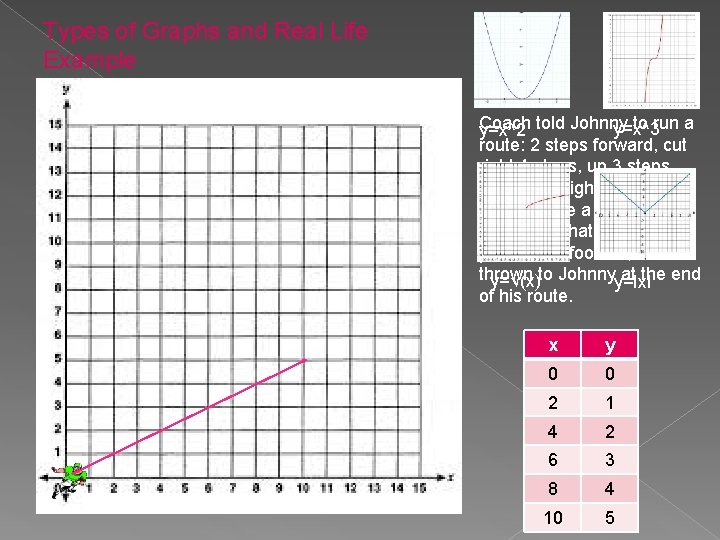
Types of Graphs and Real Life Example Coach to run a y=x^3 y=x^2 told Johnny route: 2 steps forward, cut right 4 steps, up 3 steps, and to the right again 6 steps. Make a table of the (x, y) pairs that are on the path of the football, if it is thrown at the end y=√(x)to Johnnyy=Ix. I of his route. x y 0 0 2 1 4 2 6 3 8 4 10 5

Transformational Graphing: Inside vs. Outside the Argument � Vertical Compression by 1/2 f(x) � Horizontal Compression by 1/2 f(2 x) � Vertical Stretch by 2 � � � � Horizontal Stretch by 2 Reflection over x-axis Reflection over y-axis Shift right 1 Shift left 1 Shift up 1 Shift down 1 2 f(x) f([1/2]x) -f(x) f(-x) f(x-1) f(x+1) f(x)+1 f(x)-1

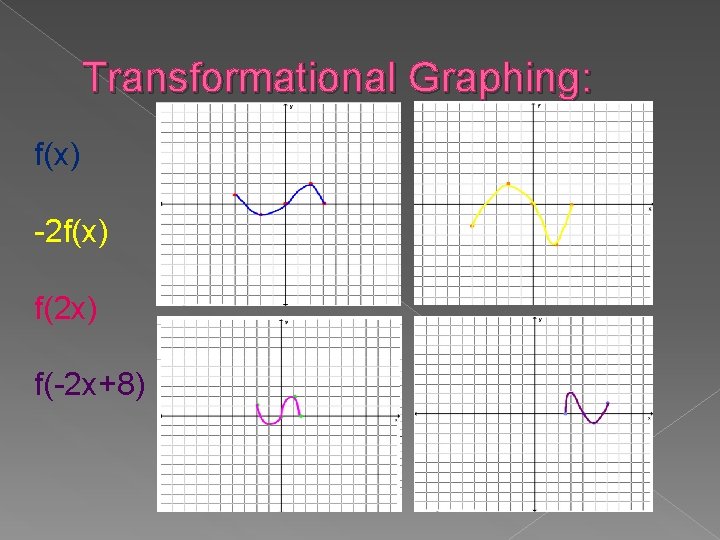
Transformational Graphing: f(x) -2 f(x) f(2 x) f(-2 x+8)

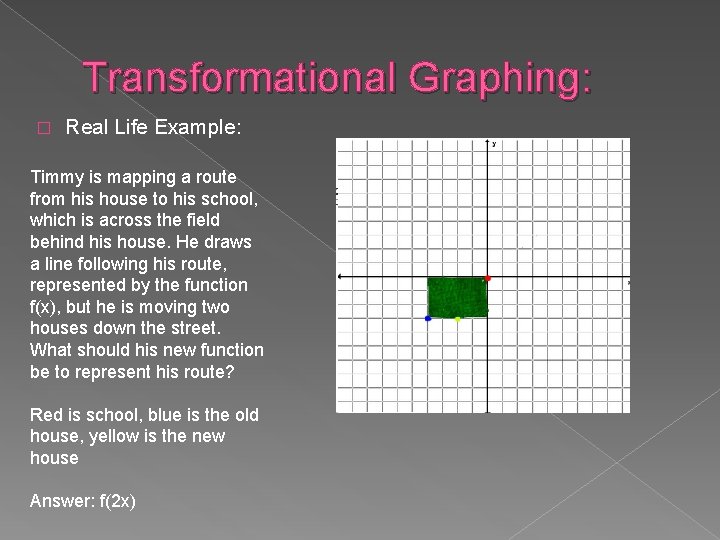
Transformational Graphing: � Real Life Example: Timmy is mapping a route from his house to his school, which is across the field behind his house. He draws a line following his route, represented by the function f(x), but he is moving two houses down the street. What should his new function be to represent his route? Red is school, blue is the old house, yellow is the new house Answer: f(2 x)

Wrapping it Up � The most important thing we learned is how to solve limits involving infinity. First, we learned the longer way and the Sources: reasoning behind the math. Then, we learned a shortcut to http: //www. mathsisfun. com/definitions/quadrant-graph. html speed up the process. http: //accelerateu. org/resourceguides/math/m 8_38. gif Textbook http: //www. sosmath. com/calculus/limcon 04/limcon 04. html http: //www. mathsisfun. com/calculus/limit s-infinity. html http: //tutorial. math. lamar. edu/Classes/Ca lc. I/Limits. At. Infinity. I. aspx -Patrick JMT youtube channel http: //jwilson. coe. uga. edu/EMAT 6680 Fa 07/Gilbert/Assig nment%202/Gayle-2_files/image 004. png http: //upload. wikimedia. org/wikibooks/en/archive/2/26/2 0061012185938!Y%3 DX%5 E 3. svg http: //jmckennonmth 212 s 09. files. wordpress. com/2009/0 3/sqroot-of-x 1. png%3 Fw%3 D 354%26 h%3 D 379 http: //media 1. shmoop. com/images/algebraii/alg 2_ch 2_narr_graphik_31. png http: //kartoweb. itc. nl/geometrics/Bitmaps/2 D%20 Cartesi an%20 coordinate%20 system. gif http: //mathworld. wolfram. com/images/epsgif/Interval_1000. gif http: //accelerateu. org/resourceguides/math/m 8_38. gif