Transformations and Symmetry Reflection Symmetry If the figure

Transformations and Symmetry

Reflection Symmetry • If the figure can be reflected over a line in such a way that the resulting image, coincides with the original, can you fold the figure over this line to get it to lie on top of itself • Place a mirror on the line to complete the figure

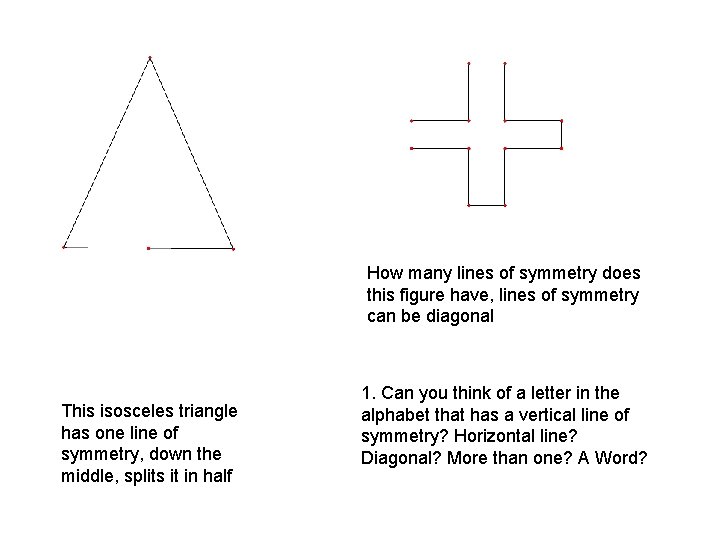
How many lines of symmetry does this figure have, lines of symmetry can be diagonal This isosceles triangle has one line of symmetry, down the middle, splits it in half 1. Can you think of a letter in the alphabet that has a vertical line of symmetry? Horizontal line? Diagonal? More than one? A Word?

Rotational Symmetry • If a figure can be rotated about a point in such a way that its rotated image coincides with the original figure before turning 360 degree • N-fold rotation, n is how many times you can rotate the figure, need to rotate at least twice • Turn a square around 4 times and they all look the same • Turn a rectangle around 2 times, 2 -fold rotation

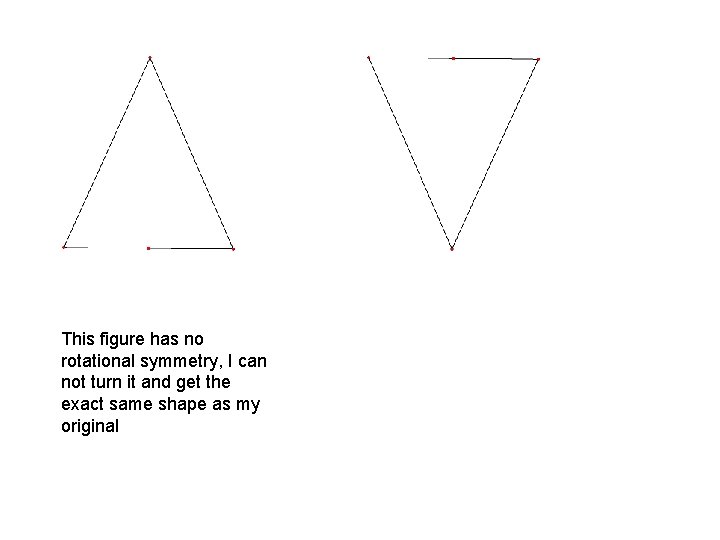
This figure has no rotational symmetry, I can not turn it and get the exact same shape as my original

How many times can you rotate this figure and get the same shape, do not count the original, but count it when you return to the original position Can you think of a letter, figure or word that has rotational symmetry?

• Rigid Transformation – when you transform the figure and get a congruent image, same rule to all points • Non-Rigid Transformation – you transform the figure and get a similar or non congruent figure, when you enlarge or shrink a figure, different rule to all points

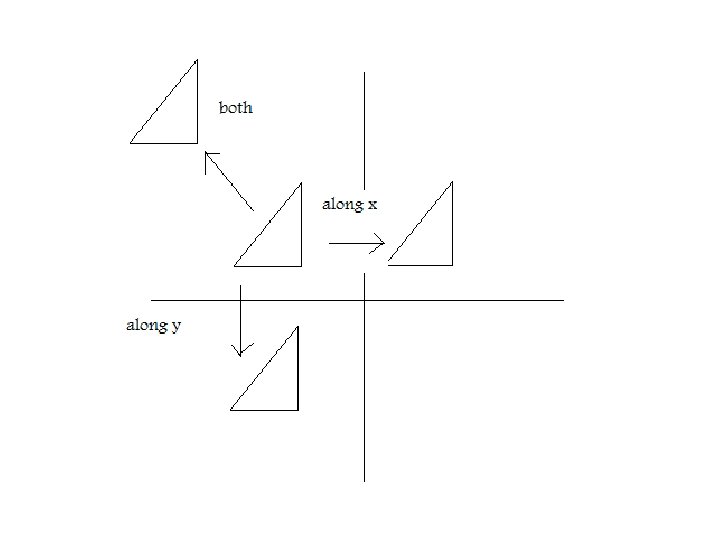
Translation • To move a figure along the x-axis, the y-axis or both • Moving a figure along the x-axis all the x coordinates are changed the same (same rule), all subtracted 4 • Moving a figure along the y-axis all the y coordinates are changed the same, all added 3 • Moving a figure on both the x and y, all points on x moved the same, all points on y moved the same

Rotational Transformation • Rotate the figure around a fixed point a fixed amount of degrees • Can rotate clockwise or counter clockwise • We will only discuss 90, 180 and 270 degrees

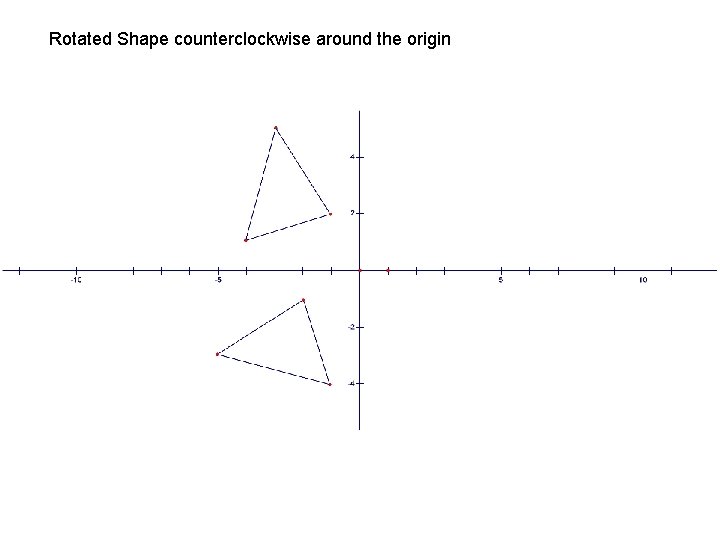
Rotated Shape counterclockwise around the origin

Reflection Transformation • Reflect figure over a fixed line to get a mirror image of the figure • The line the figure is reflected over is the perpendicular bisector of the segment connecting the figure and the image • Mirror the distance on each side and flip the figure

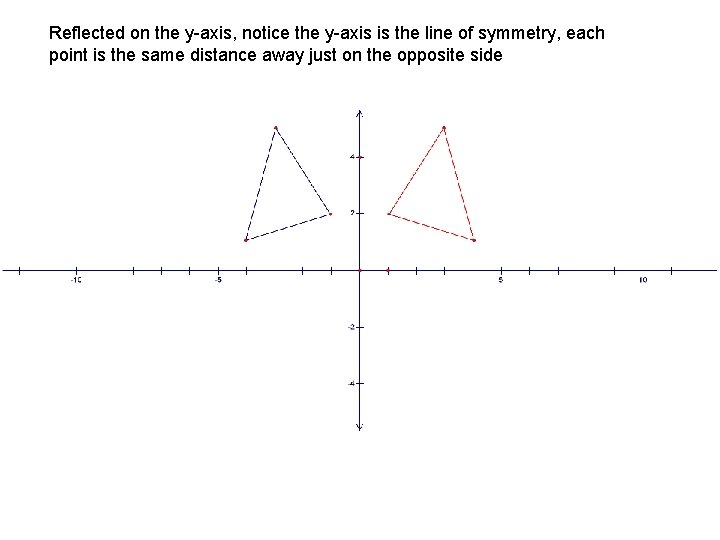
Reflected on the y-axis, notice the y-axis is the line of symmetry, each point is the same distance away just on the opposite side

Multi Step Transformations Some multi step transformations result in the same single transformation Do two translations could be rewritten as a single translation A reflection over x then y axis could be a rotation of 180 Combination of 2 different transformations