Transformation Translation Reflection Rotation and Dilatation 1 After

Transformation (Translation, Reflection, Rotation, and Dilatation) 1

After see these slides you can: Determine map or image of result curve of a Translation, Reflection, Rotation, or Dilatation 2

Transformation To move a point or shape on a plane can be done by transformation. Transformation T on a plane is ‘mapping’ every P point on plane become P’ on the same plane. P’ is called image or map of P 3

Kind of Transformation: a. Translation b. Reflection c. Rotation d. Dilatation *) will be discussed today 4

Translation means friction 5

If translation T = mapping P (x, y) to P´ (x’, y’) then x’ = x + a and y’ = y + b Is written into matrix: 6

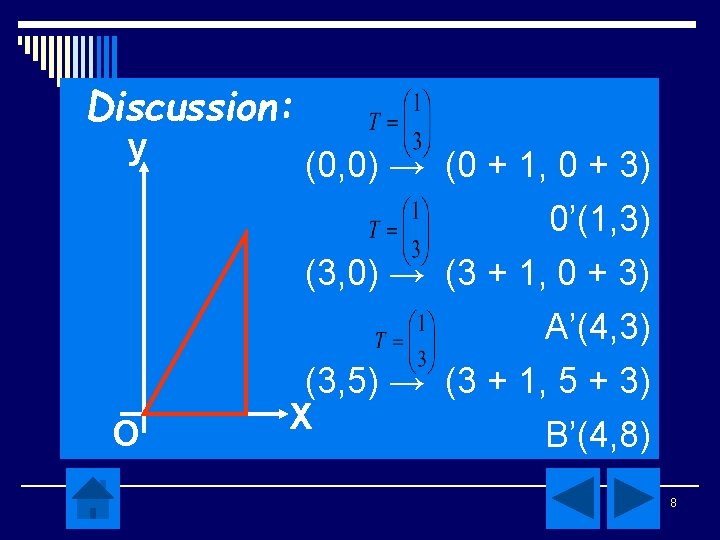
Example 1 Known triangle OAB with coordinate O(0, 0), A(3, 0), and B(3, 5). Find the image coordinate of triangle OAB if it is translated by T = 7

Discussion: y (0, 0) → (0 + 1, 0 + 3) 0’(1, 3) (3, 0) → (3 + 1, 0 + 3) A’(4, 3) O (3, 5) → (3 + 1, 5 + 3) X B’(4, 8) 8

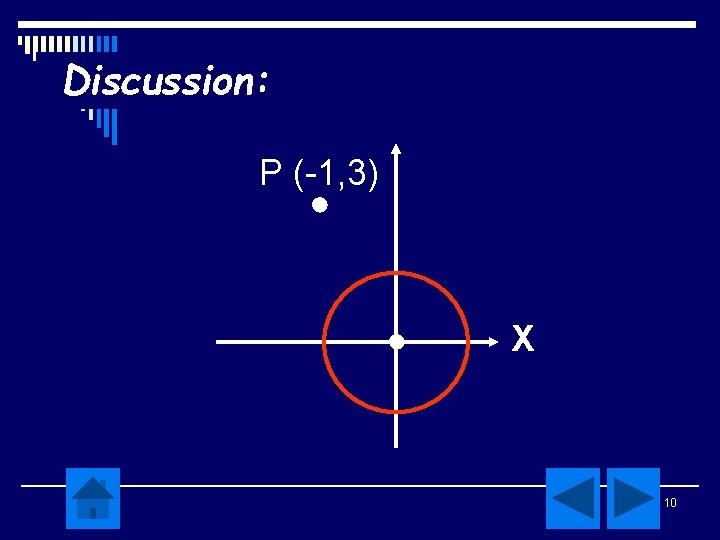
Example 2 Image of circle equation x 2 + y 2 = 25 by translation T = is…. 9

Discussion: P (-1, 3) ● ● X 10

Because translation T = so x’ = x – 1 → x = x’ + 1. …. (1) y’ = y + 3 → y = y’ – 3…. . (2) (1) and (2) are substituted into (2) x 2 + y 2 = 25 can be found (3) (x’ + 1)2 + (y’ – 3)2 = 25; (4)Then the image is: (x + 1)2 + (y – 3)2 = 25 11

Example 3 By a translation, map of point (1, -5) is (7, -8). The image curve of y = x 2 + 4 x – 12 by that translation is…. 12

Discussion If translation T = Image point (1, -5) by translation T is (1 + a, -5 + b) = (7, -8) 1+ a = 7 → a = 6 -5+ b = -8 → b = -3 13

a = 6 and b = -3 so the translation is T = Because T = Then x’ = x + 6 → x = x’ – 6 y’ = y – 3 → y = y’ + 6 14

x = x’ – 6 and y = y’ + 3 are substituted into y = x 2 + 4 x – 12 y’ + 3 = (x’ – 6)2 + 4(x’ – 6) – 12 y’ + 3 = (x’)2 – 12 x’ + 36 + 4 x’ - 24 -12 y’ = (x’)2 – 8 x’ – 3 So, the image is: y = x 2 – 8 x – 3 15

Rotation means move by circular path determine by centrum and angular magnitude 16

Rotation with centre O(0, 0) P(x, y) is rotated as counter clockwise with centre O(0, 0) and can be found image P’(x’, y’) so: x’ = xcos - ysin y’ = xsin + ycos 17

If angular angle = ½π (the rotation is signed with R½π) then x’ = - y and y’ = x In matrix: so R½π = 18

Example 1 Equation of image line x + y = 6 after it is rotated in centre coordinate with angular angle +90 o, is…. 19

Discussion: R+90 o means: x’ = -y → y = -x’ y’ = x → x = y’ are substituted into: x + y = 6 y’ + (-x’) = 6 y’ – x’ = 6 → x’ – y’ = - 6 So the image line x + y = 6 is: x–y=-6 20

Example 2 Equation of image line 2 x - y + 6 = 0 after it is rotated in centre coordinate with angular angle -90 o , is…. 21

Discussion: R-90 o means: x’ = xcos(-90) – ysin(-90) y’ = xsin(-90) + ycos(-90) x’ = 0 – y(-1) = y y’ = x(-1) + 0 = -x’ or with matrix: 22

R-90 o means: x’ = y → y = x’ y’ = -x → x = -y’ substituted into: 2 x - y + 6 = 0 2(-y’) - x’ + 6 = 0 -2 y’ – x’ + 6 = 0 x’ + 2 y’ – 6 = 0 So, the image line 2 x - y + 6 = 0 is: x+y– 6=0 23

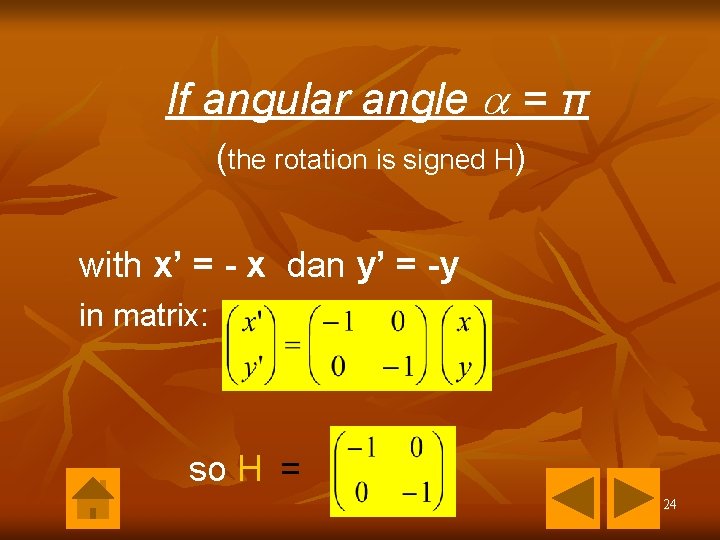
If angular angle = π (the rotation is signed H) with x’ = - x dan y’ = -y in matrix: so H = 24

Example Equation of image parabola y = 3 x 2 – 6 x + 1 after it is rotated in centre coordinate with angular angle +180 o, is…. 25

Discussion H means: x’ = -x → x = -x’ y’ = -y → y = -y’ substituted into: y = 3 x 2 – 6 x + 1 -y’= 3(-x’)2 – 6(-x’) + 1 -y’= 3(x’)2 + 6 x + 1 (multiplied by -1) So, the image parabola y = 3 x 2 – 6 x + 1 : is y = - 3 x 2 – 6 x - 1 26

Dilatation is a transformation that change the size (bigger or smaller) a shape without changing its form. 27

Dilatation centre O(0, 0) and k scale factor If P (x, y) is dilatated into O(0, 0) and k scale factor the image is P’ (x’, y’) so x’ = kx and y’ = ky and it is signed with D[O, k] 28

Example Line 2 x – 3 y = 6 intersect X axis at A and intersect Y axis at B. Because of the dilatation D[O, -2], A become A’ and B become B’. Find the area of OA’B’ 29

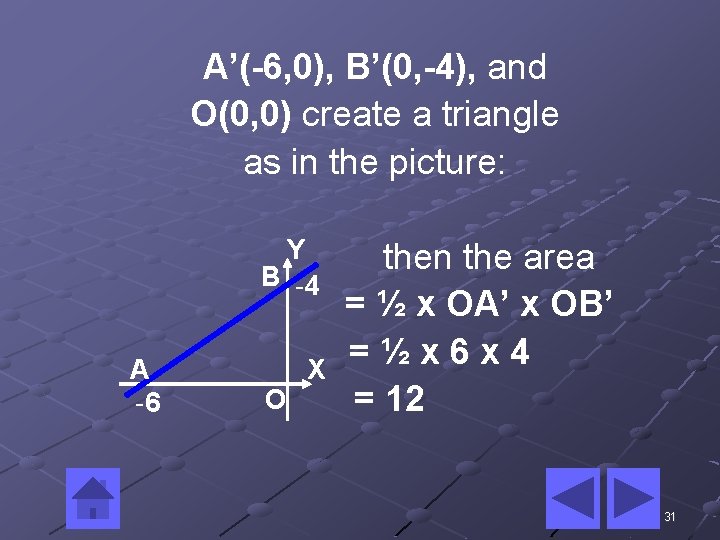
• Discussion Line 2 x – 3 y = 6 intersect X axis at A(3, 0), and through Y axis at B(0, 2) because the dilatation D[O, -2] then A’ (kx, ky)→ A’(-6, 0) and B’ (kx, ky) → B’(0, -4) 30

A’(-6, 0), B’(0, -4), and O(0, 0) create a triangle as in the picture: Y B -4 A -6 O X then the area = ½ x OA’ x OB’ =½x 6 x 4 = 12 31

Dilatation with centre P(a, b) and k scale factor The image is: x’ = k (x – a) + a and y’ = k (y – b) + b signed with [P (a, b) , k] 32

Example A(-5, 13) is dilatated with [P, ⅔] become A’. If coordinate P(1, -2), then coordinate A’ is…. 33

Inverse Transformation To determine image of curve by transformation written in matrix form, we can use inverse transformation 36

Example Map of line x – 2 y + 5 = 0 by transformation that is stated with matrix is…. 37

Discussion A(x, y) A’(x’ y’) Remember: A = BX so X = B-1. A 38

get: x = 3 x’ – y’ and y = -2 x’ + y’ 39

x = 3 x’ – y’ and y = -2 x’ + y’ are substituted into x – 2 y + 5 = 0 3 x’ – y’ – 2(-2 x’ + y’) + 5 = 0 3 x’ – y’ + 4 x’ – 2 y’ + 5 = 0 7 x’ – 3 y’ + 5 = 0 So, the image is: 7 x – 3 y + 5 = 0 40

Keep analytic and faithful 41