Transformation of Discrete Time Signals This module shows

Transformation of Discrete Time Signals This module shows how different operations such as amplitude scaling, time reversing and time shifting transform a discrete time signal. Course Name: Signals and Systems Level: UG Authors Phani Swathi Mentor Prof. Saravanan Vijayakumaran

Learning Objectives After interacting with this Learning Object, the learner will be able to: • Perform shifting and/or scaling factors required, plot the output of specified amplitude and/or time transformation on the signal, for a given discrete time signal. • Identify the type of transformation performed, for a given transformation equation. • Plot the outputs of amplitude and time transformations on the signal, for a given discrete time signal and transformation equation. • Identify the type of transformation performed, for a given input signal and transformed signal

Theory button content A discrete time signal can be manipulated by modifying or transforming its amplitude or time variable. The most common time transformations include shifting, scaling and reversal. Amplification is a common type of amplitude transformation. In time shifting, n is replaced by (n-no), where no can be any integer. If no is positive, the signal is said to be delayed. e. g. x(n-1), where signal is shifted to the right by 1 unit. If no is negative, the signal is said to be advanced. e. g. x(n+1), where signal is shifted to the left by 1 unit. In time scaling, n is replaced by a multiple of n i. e. (α n), where α can be any real number. If α>1, the signal is said to be compressed in time e. g. x(2 n), where signal is compressed twice about n=0. If 0<α<1, the signal expands in time e. g. x(0. 5 n) , where signal is stretched about n=0. In time reversal, n is replaced by -n. The signal is mirrored about n=0 In amplitude scaling, signal is magnified by a real value e. g. x(n) is replaced by β x(n). If β>1, the signal is said to be amplified e. g. 2 x(n), where signal amplitude is doubled. If 0<β<1, the signal is said to be attenuated e. g. 0. 5 x(n), where signal amplitude is halved. Multiple transformations can be applied to a signal in a certain sequence to manipulate it in a particular way. The sequence of operation in time transformations is significant. x(n) Reversed Reversal & Delaying: x(– n) Delayed by 1 x(n) Delayed by 1 X(n) Scaled by 2 Scaling & Delaying: x(n) Delayed by 1 X(n– 1) x(2 n) x(– (n– 1)) x(– n+1); Reversed Delayed by 1 x( n– 1) Scaled by 2 x((– n)– 1) x(–n– 1) x(2 (n– 1)) x(2 n– 2); x((2 n)– 1) x(2 n – 1)

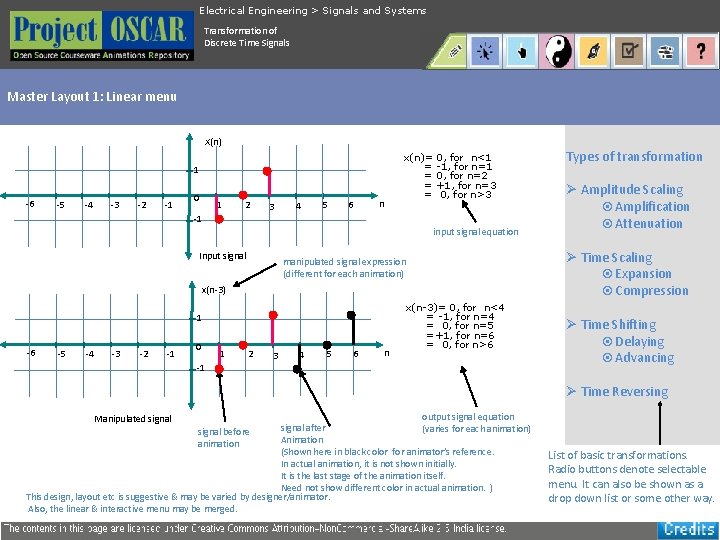
Electrical Engineering > Signals and Systems Transformation of Discrete Time Signals Master Layout 1: Linear menu Input signal expression x(t) X(n) 1 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 n x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 -1 input signal equation Input signal manipulated signal expression (different for each animation) x(n-3) 1 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 n x(n-3)= 0, for n<4 = -1, for n=4 = 0, for n=5 =+1, for n=6 = 0, for n>6 -1 Types of transformation Ø Amplitude Scaling ¤Amplification ¤Attenuation Ø Time Scaling ¤Expansion ¤Compression Ø Time Shifting ¤Delaying ¤Advancing Ø Time Reversing output signal equation signal after (varies for each animation) signal before Animation animation (Shown here in black color for animator’s reference. In actual animation, it is not shown initially. It is the last stage of the animation itself. Need not show different color in actual animation. ) This design, layout etc is suggestive & may be varied by designer/animator. Also, the linear & interactive menu may be merged. Manipulated signal List of basic transformations. Radio buttons denote selectable menu. It can also be shown as a drop down list or some other way.

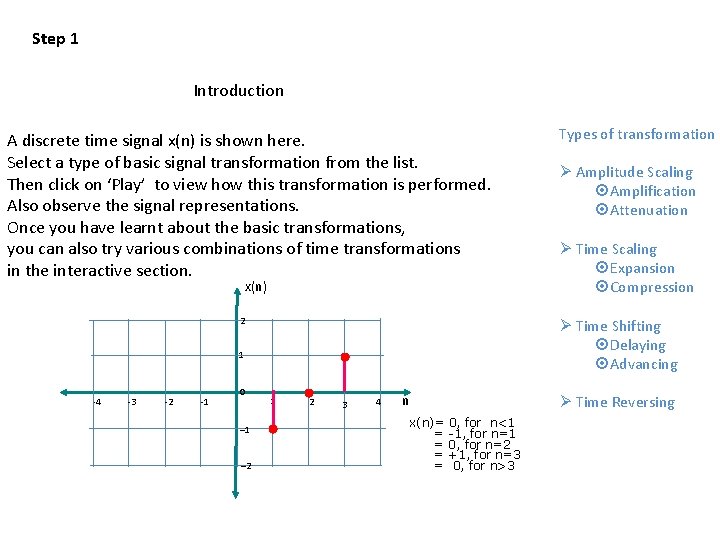
Step 1 Introduction A discrete time signal x(n) is shown here. Select a type of basic signal transformation from the list. Then click on ‘Play’ to view how this transformation is performed. Also observe the signal representations. Once you have learnt about the basic transformations, you can also try various combinations of time transformations in the interactive section. x(n) 2 -3 -2 -1 0 – 1 – 2 Ø Amplitude Scaling ¤Amplification ¤Attenuation Ø Time Scaling ¤Expansion ¤Compression Ø Time Shifting ¤Delaying ¤Advancing 1 -4 Types of transformation 1 2 3 4 n Ø Time Reversing x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3

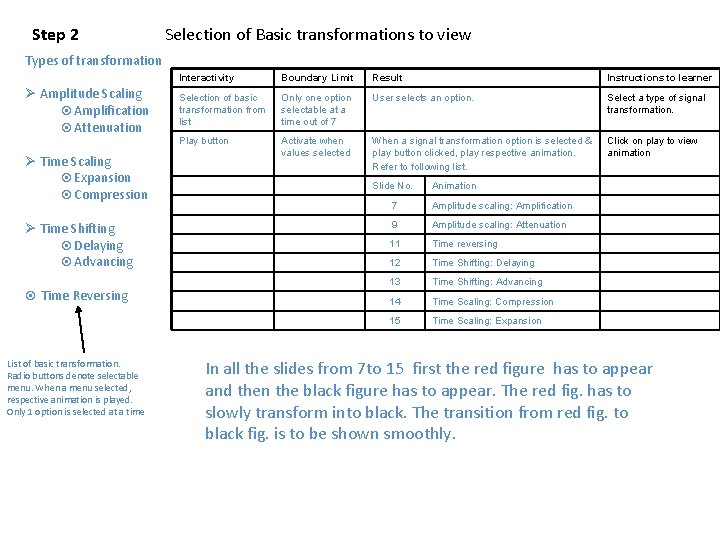
Step 2 Selection of Basic transformations to view Types of transformation Ø Amplitude Scaling ¤Amplification ¤Attenuation Ø Time Scaling ¤Expansion ¤Compression Ø Time Shifting ¤Delaying ¤Advancing ¤ Time Reversing List of basic transformation. Radio buttons denote selectable menu. When a menu selected, respective animation is played. Only 1 option is selected at a time Interactivity Boundary Limit Result Instructions to learner Selection of basic transformation from list Only one option selectable at a time out of 7 User selects an option. Select a type of signal transformation. Play button Activate when values selected When a signal transformation option is selected & play button clicked, play respective animation. Refer to following list. Click on play to view animation Slide No. Animation 7 Amplitude scaling: Amplification 9 Amplitude scaling: Attenuation 11 Time reversing 12 Time Shifting: Delaying 13 Time Shifting: Advancing 14 Time Scaling: Compression 15 Time Scaling: Expansion In all the slides from 7 to 15 first the red figure has to appear and then the black figure has to appear. The red fig. has to slowly transform into black. The transition from red fig. to black fig. is to be shown smoothly.

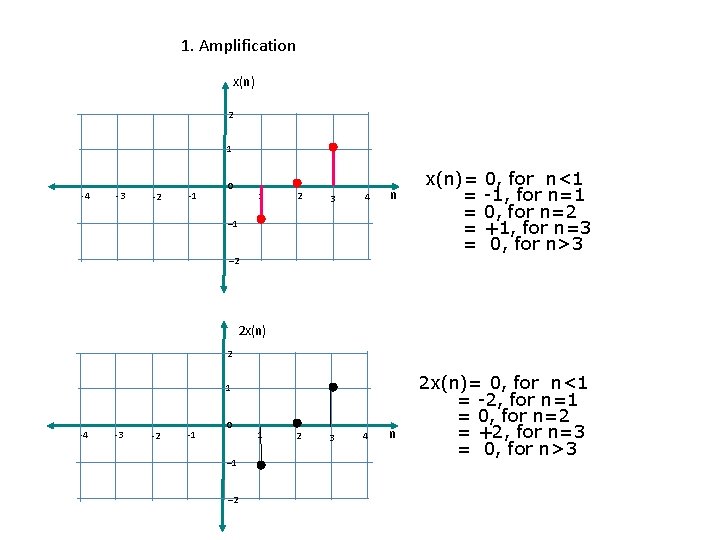
1. Amplification x(n) 2 1 -4 -3 -2 -1 0 1 2 3 4 n – 1 x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 – 2 2 x(n) 2 1 -4 -3 -2 -1 0 – 1 – 2 1 2 3 4 n 2 x(n)= 0, for n<1 = -2, for n=1 = 0, for n=2 = +2, for n=3 = 0, for n>3

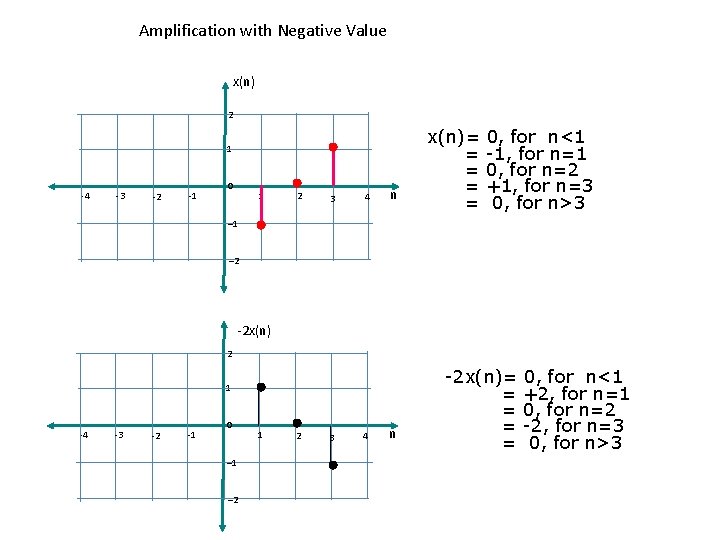
Amplification with Negative Value x(n) 2 1 -4 -3 -2 -1 0 1 2 3 4 n x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 – 1 – 2 -2 x(n) 2 1 -4 -3 -2 -1 0 – 1 – 2 1 2 3 4 n -2 x(n)= 0, for n<1 = +2, for n=1 = 0, for n=2 = -2, for n=3 = 0, for n>3

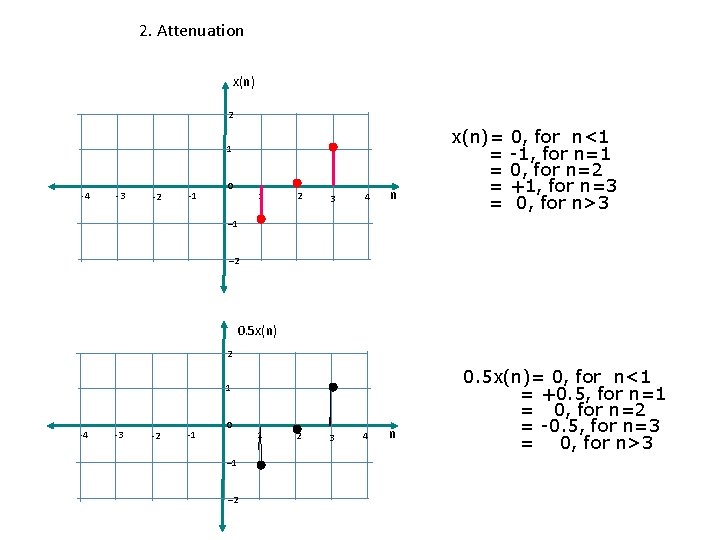
2. Attenuation x(n) 2 1 -4 -3 -2 -1 0 1 2 3 4 n x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 – 1 – 2 0. 5 x(n) 2 1 -4 -3 -2 -1 0 – 1 – 2 1 2 3 4 n 0. 5 x(n)= 0, for n<1 = +0. 5, for n=1 = 0, for n=2 = -0. 5, for n=3 = 0, for n>3

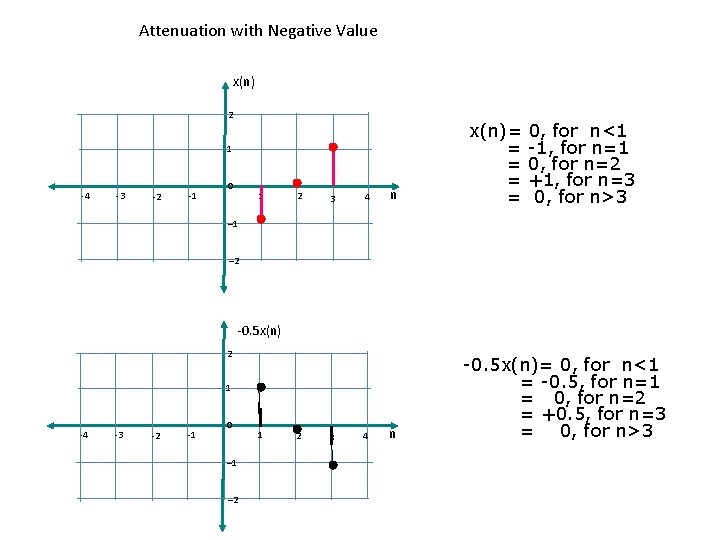
Attenuation with Negative Value x(n) 2 1 -4 -3 -2 -1 0 1 2 3 4 n x(n)= = = 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 – 1 – 2 -0. 5 x(n) 2 1 -4 -3 -2 -1 0 – 1 – 2 1 2 3 4 n -0. 5 x(n)= 0, for n<1 = -0. 5, for n=1 = 0, for n=2 = +0. 5, for n=3 = 0, for n>3

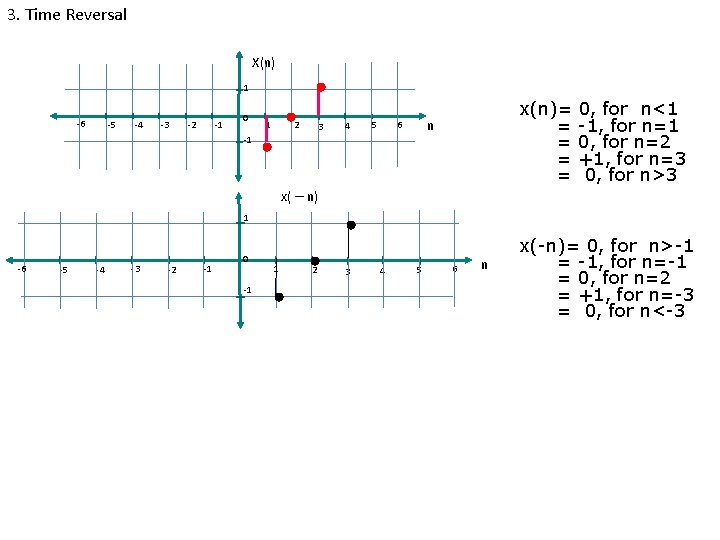
3. Time Reversal X(n) 1 -6 -5 -4 -3 -1 -2 0 1 2 3 4 5 x(n)= = = n 6 -1 x( – n) 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 1 -6 -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 6 n x(-n)= 0, for n>-1 = -1, for n=-1 = 0, for n=2 = +1, for n=-3 = 0, for n<-3

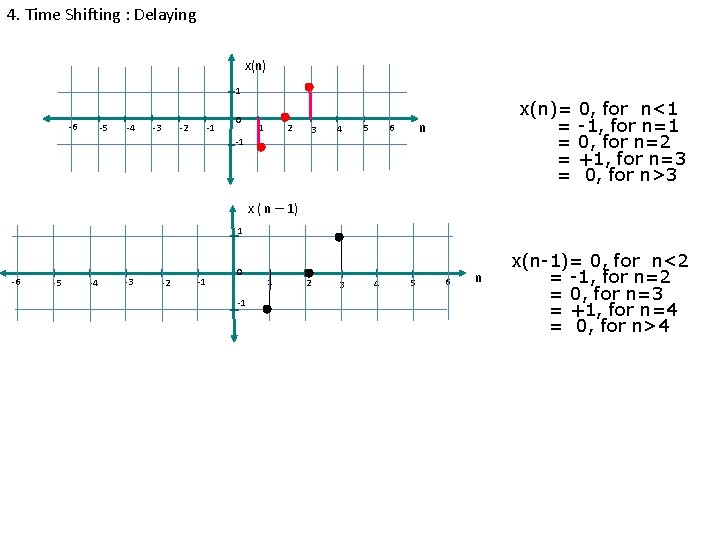
4. Time Shifting : Delaying x(n) 1 -6 -5 -4 -3 -1 -2 0 1 2 3 4 n 6 5 x(n)= = = -1 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 x ( n – 1) 1 -6 -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 6 n x(n-1)= 0, for n<2 = -1, for n=2 = 0, for n=3 = +1, for n=4 = 0, for n>4

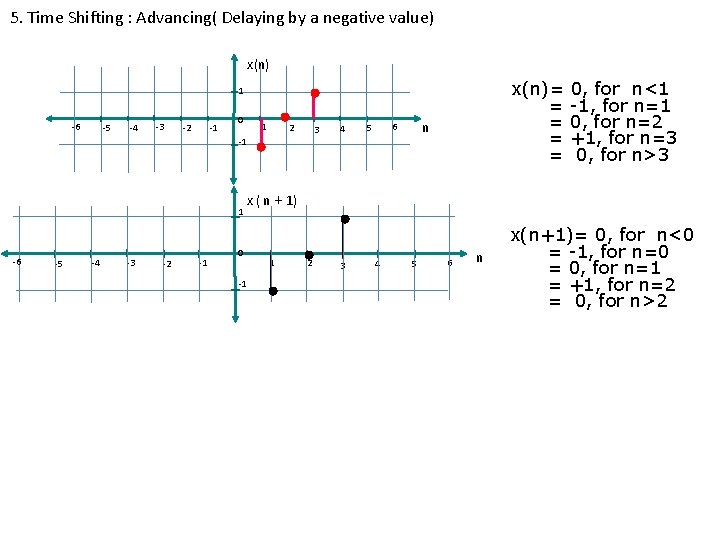
5. Time Shifting : Advancing( Delaying by a negative value) x(n)= = = 1 -6 -5 -4 -3 -1 -2 0 1 2 3 4 n 6 5 -1 1 -6 -5 -4 -3 -2 -1 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 x ( n + 1) 0 -1 1 2 3 4 5 6 n x(n+1)= 0, for n<0 = -1, for n=0 = 0, for n=1 = +1, for n=2 = 0, for n>2

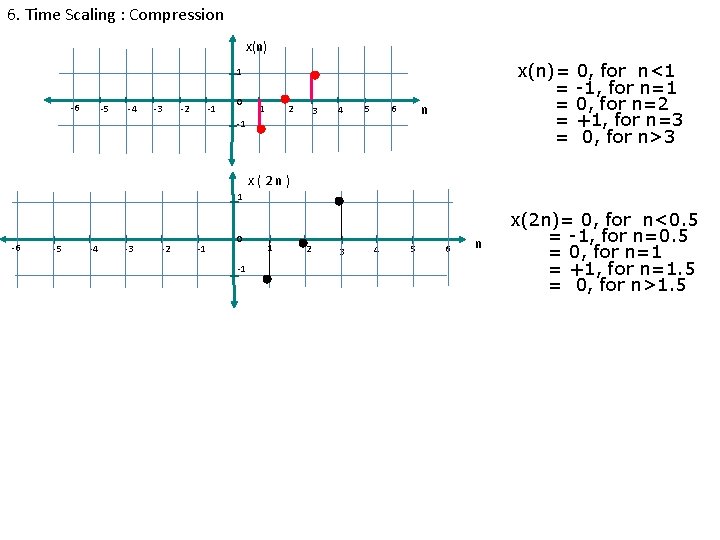
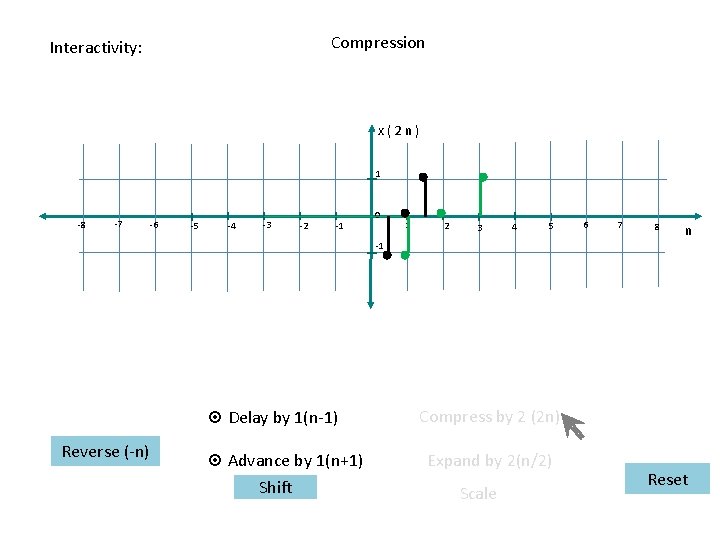
6. Time Scaling : Compression x(n)= = = 1 -6 -5 -4 -3 -1 -2 0 1 2 3 4 n 6 5 -1 0, for n<1 -1, for n=1 0, for n=2 +1, for n=3 0, for n>3 x(2 n) 1 -6 -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 6 n x(2 n)= 0, for n<0. 5 = -1, for n=0. 5 = 0, for n=1 = +1, for n=1. 5 = 0, for n>1. 5

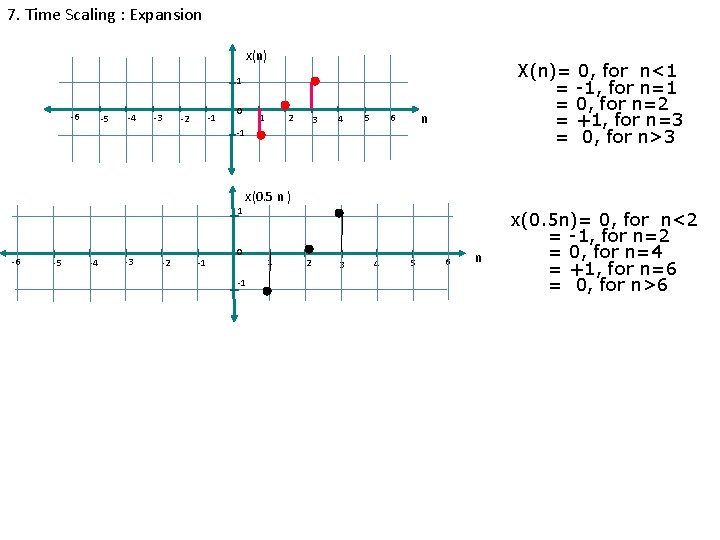
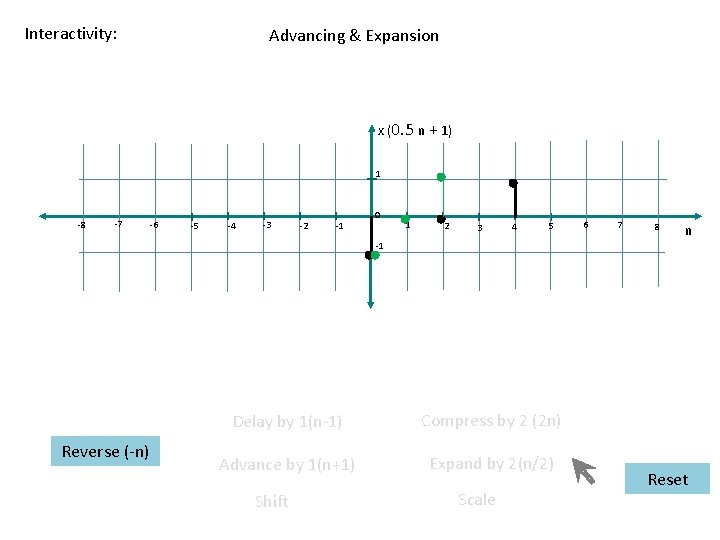
7. Time Scaling : Expansion x(n) X(n)= 0, for n<1 = -1, for n=1 = 0, for n=2 = +1, for n=3 = 0, for n>3 1 -6 -5 -4 -3 -1 -2 0 1 2 3 4 n 6 5 -1 x(0. 5 n ) 1 -6 -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 6 n x(0. 5 n)= 0, for n<2 = -1, for n=2 = 0, for n=4 = +1, for n=6 = 0, for n>6

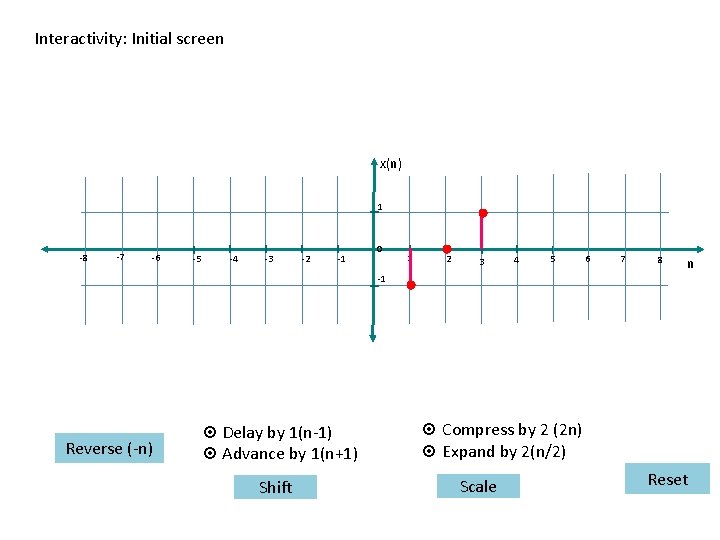
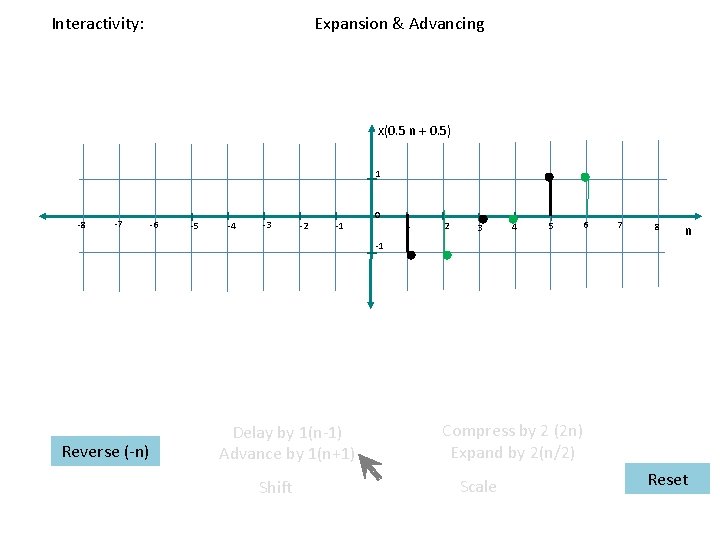
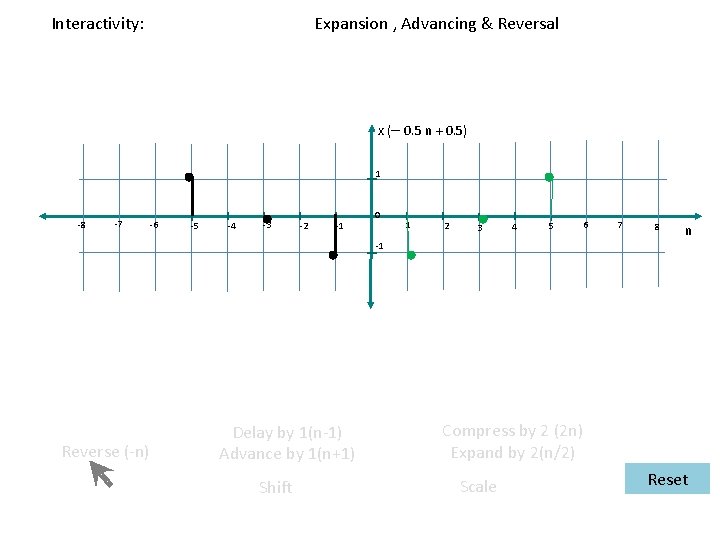
Electrical Engineering > Signals and Systems Transformation of Discrete Time Signals Master Layout 2: Interactive menu Input signal expression x(t) Reverse (-n) X(n-3) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 -1 8 n Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) 3 options ( reverse, shift, scale) 2 sub-options in Shift (delay & advance) and Scale ( compress & expand) Each of the 3 options selected only once. As option selected, animation is shown and that option is disabled When next option is selected, its animation is shown. When reset is selected, the signal is reset and all the 3 options are enabled. From slides 22 to 66 first the red fig. in slide 20 has to appear and transform into green and then to black fig. The transformation should be shown smoothly. Scale Reset

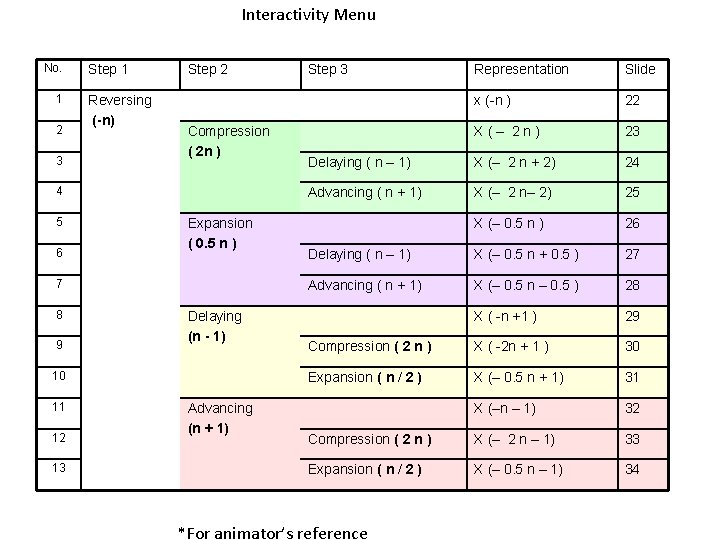
Interactivity Menu No. 1 2 3 Step 1 Reversing (-n) Step 2 Compression ( 2 n ) 4 5 6 Expansion ( 0. 5 n ) 7 8 9 Delaying (n - 1) 10 11 12 13 Advancing (n + 1) Step 3 Representation Slide x (-n ) 22 X(– 2 n) 23 Delaying ( n – 1) X (– 2 n + 2) 24 Advancing ( n + 1) X (– 2 n– 2) 25 X (– 0. 5 n ) 26 Delaying ( n – 1) X (– 0. 5 n + 0. 5 ) 27 Advancing ( n + 1) X (– 0. 5 n – 0. 5 ) 28 X ( -n +1 ) 29 Compression ( 2 n ) X ( -2 n + 1 ) 30 Expansion ( n / 2 ) X (– 0. 5 n + 1) 31 X (–n – 1) 32 Compression ( 2 n ) X (– 2 n – 1) 33 Expansion ( n / 2 ) X (– 0. 5 n – 1) 34 *For animator’s reference

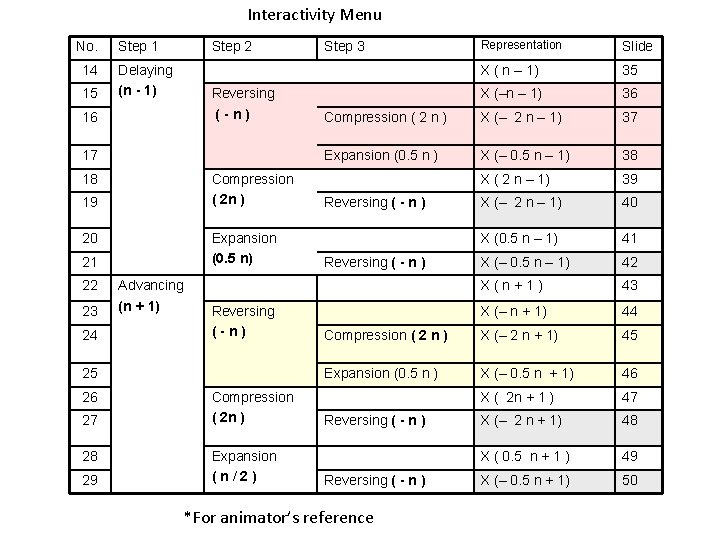
Interactivity Menu No. 14 15 Step 1 Step 2 Delaying (n - 1) Reversing (-n) 16 17 18 Compression ( 2 n ) 19 20 Expansion (0. 5 n) 21 22 23 24 Advancing (n + 1) Reversing (-n) 25 26 27 28 29 Compression ( 2 n ) Expansion (n/2) Representation Slide X ( n – 1) 35 X (–n – 1) 36 Compression ( 2 n ) X (– 2 n – 1) 37 Expansion (0. 5 n ) X (– 0. 5 n – 1) 38 X ( 2 n – 1) 39 X (– 2 n – 1) 40 X (0. 5 n – 1) 41 X (– 0. 5 n – 1) 42 X(n+1) 43 X (– n + 1) 44 Compression ( 2 n ) X (– 2 n + 1) 45 Expansion (0. 5 n ) X (– 0. 5 n + 1) 46 X ( 2 n + 1 ) 47 X (– 2 n + 1) 48 X ( 0. 5 n + 1 ) 49 X (– 0. 5 n + 1) 50 Step 3 Reversing ( - n ) *For animator’s reference

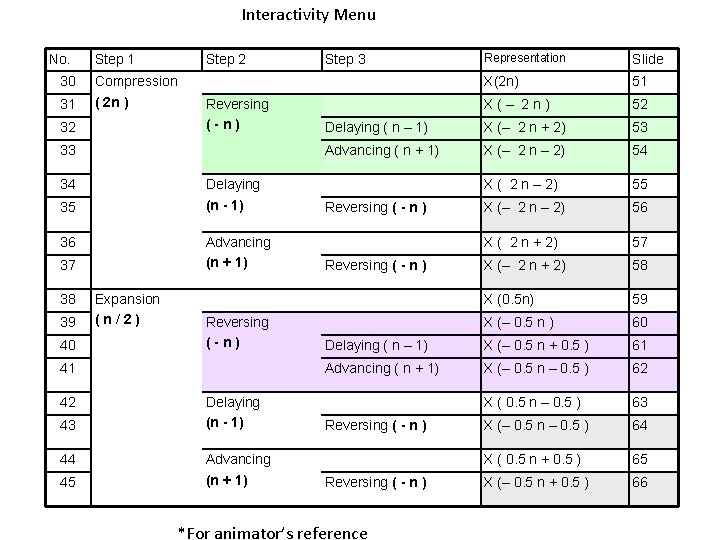
Interactivity Menu No. 30 31 Step 1 Compression ( 2 n ) 32 Step 2 Reversing (-n) 33 34 Delaying (n - 1) 35 36 Advancing (n + 1) 37 38 39 40 Expansion (n/2) Reversing (-n) 41 42 43 44 45 Delaying (n - 1) Advancing (n + 1) Representation Slide X(2 n) 51 X(– 2 n) 52 Delaying ( n – 1) X (– 2 n + 2) 53 Advancing ( n + 1) X (– 2 n – 2) 54 X ( 2 n – 2) 55 X (– 2 n – 2) 56 X ( 2 n + 2) 57 X (– 2 n + 2) 58 X (0. 5 n) 59 X (– 0. 5 n ) 60 Delaying ( n – 1) X (– 0. 5 n + 0. 5 ) 61 Advancing ( n + 1) X (– 0. 5 n – 0. 5 ) 62 X ( 0. 5 n – 0. 5 ) 63 X (– 0. 5 n – 0. 5 ) 64 X ( 0. 5 n + 0. 5 ) 65 X (– 0. 5 n + 0. 5 ) 66 Step 3 Reversing ( - n ) *For animator’s reference

Interactivity: Initial screen x(n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

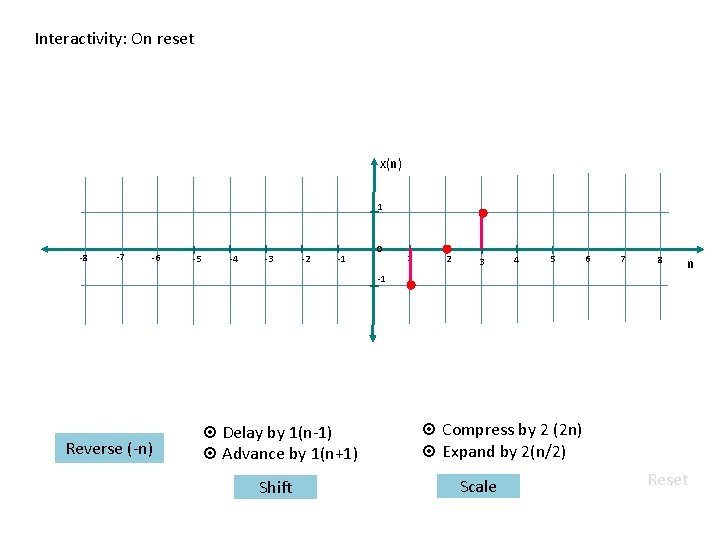
Interactivity: On reset x(n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

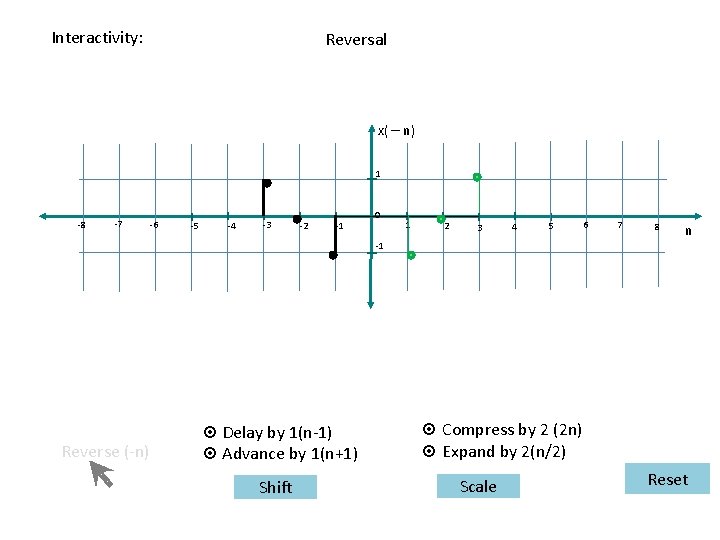
Interactivity: Reversal x( – n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

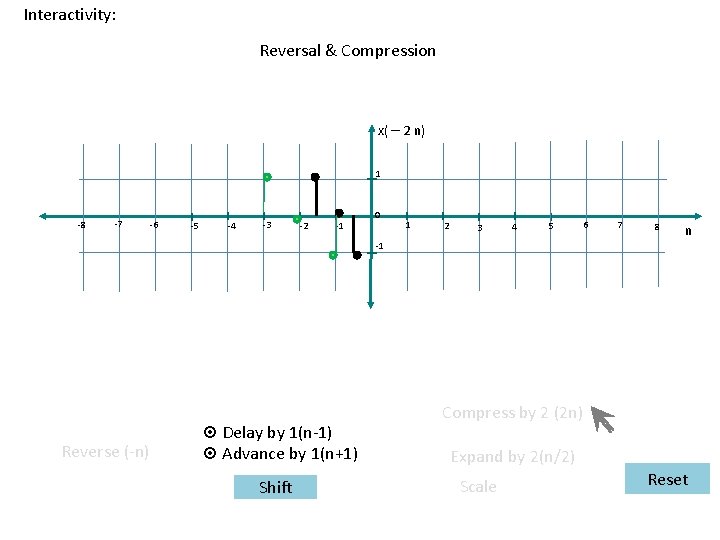
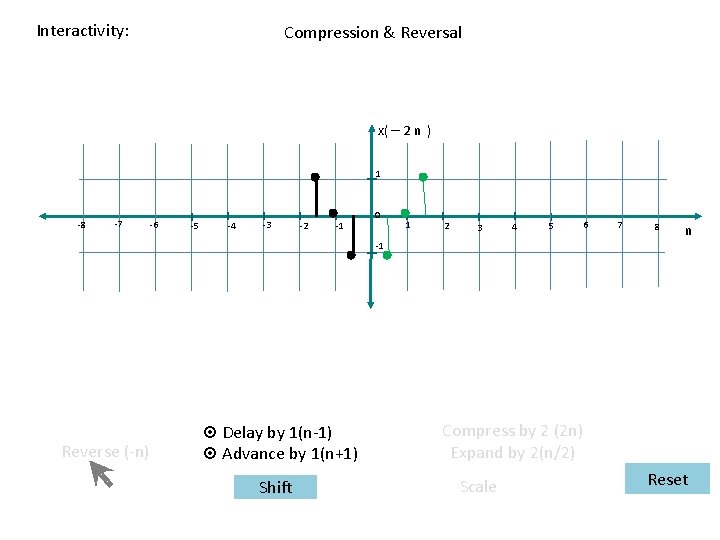
Interactivity: Reversal & Compression x( – 2 n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

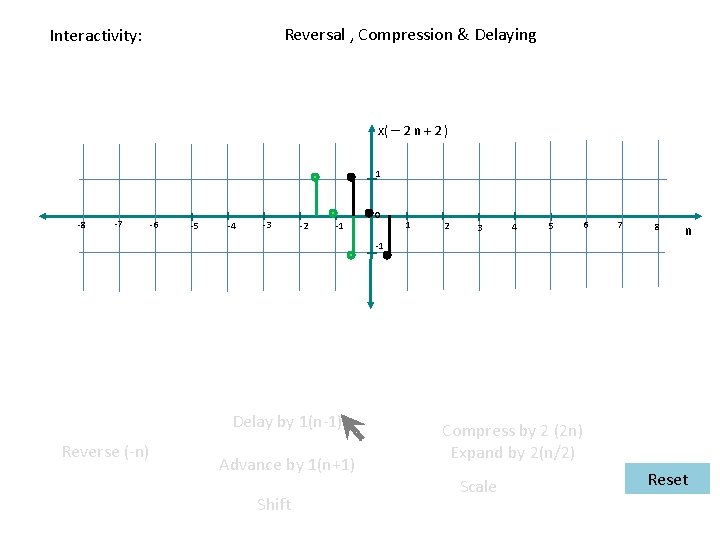
Reversal , Compression & Delaying Interactivity: x( – 2 n + 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

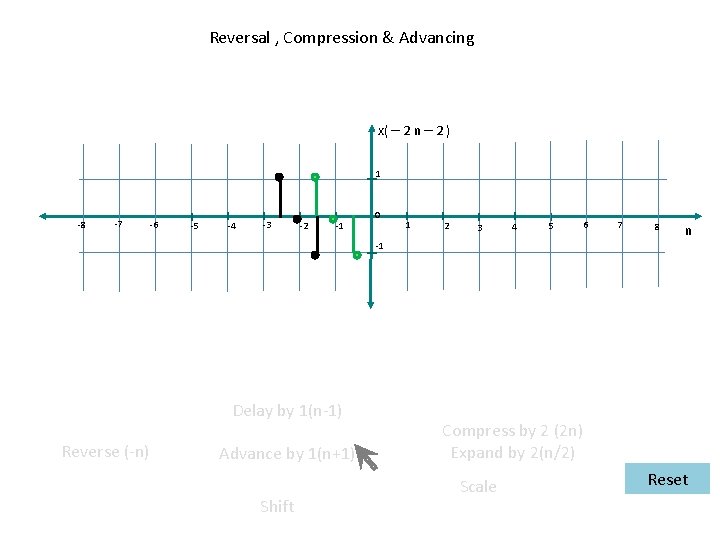
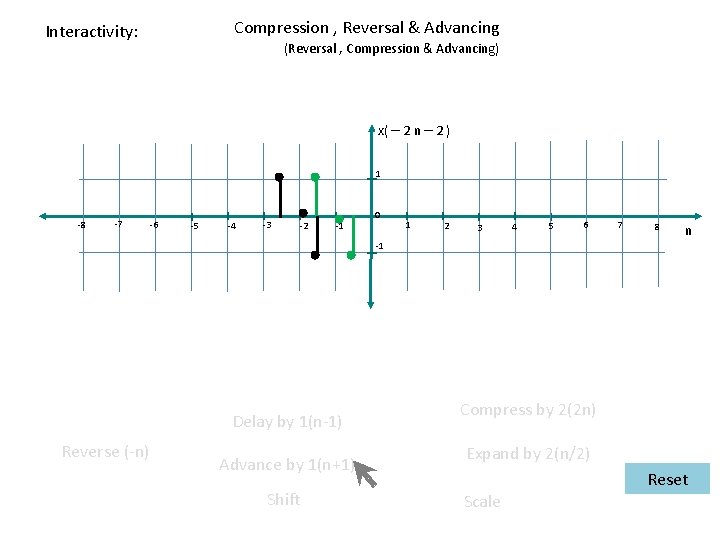
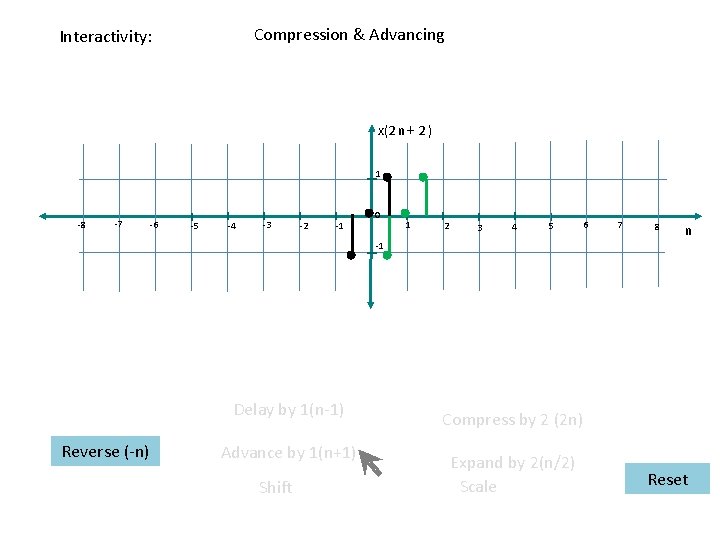
Reversal , Compression & Advancing x( – 2 n – 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

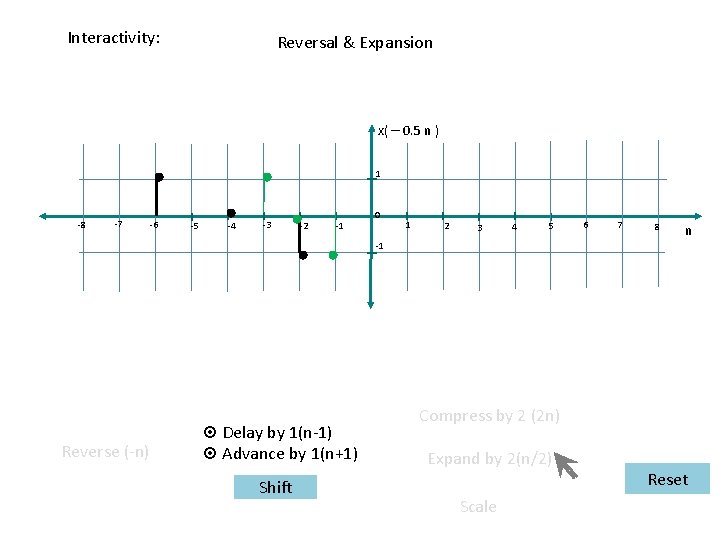
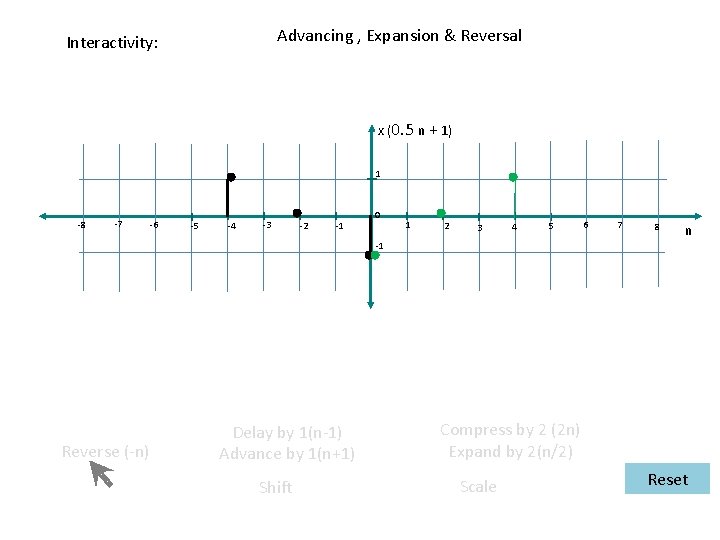
Interactivity: Reversal & Expansion x( – 0. 5 n ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

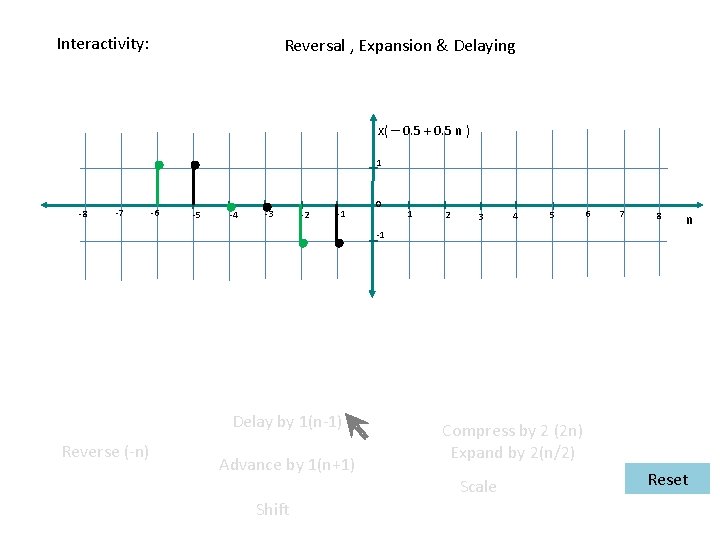
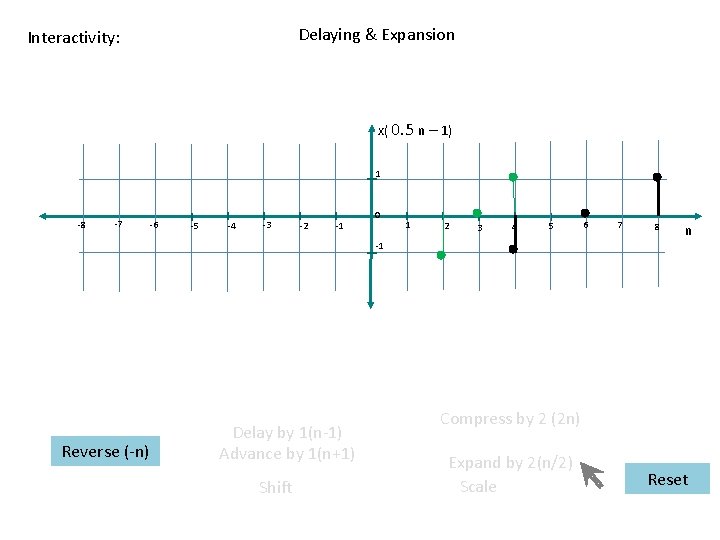
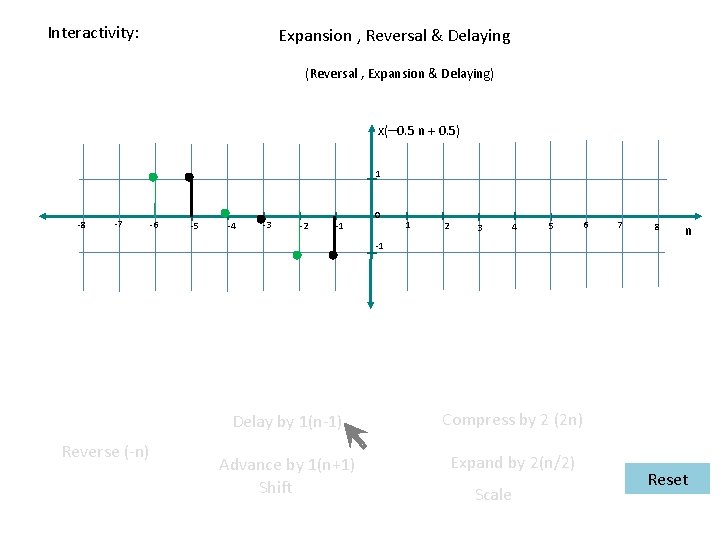
Interactivity: Reversal , Expansion & Delaying x( – 0. 5 + 0. 5 n ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

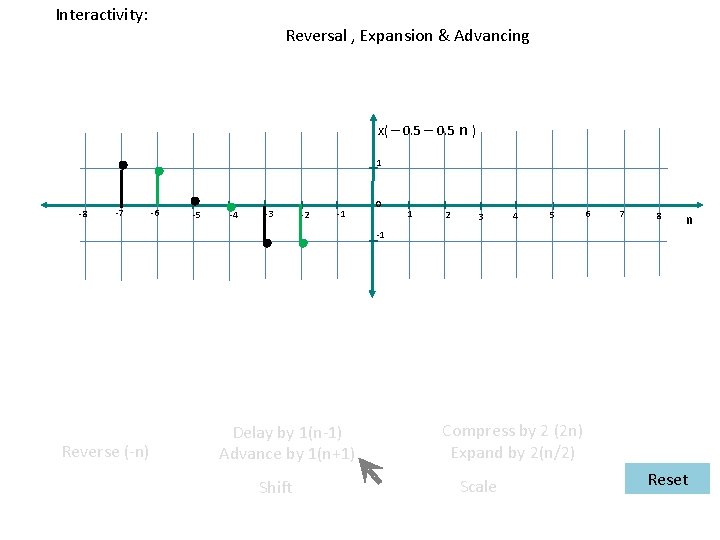
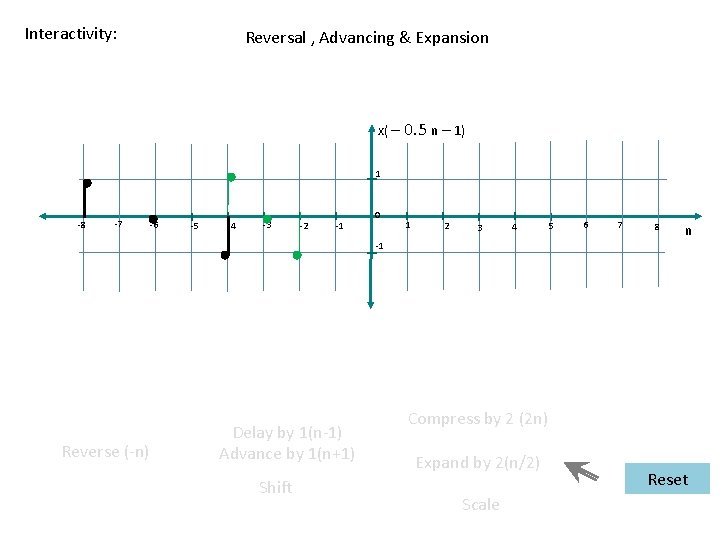
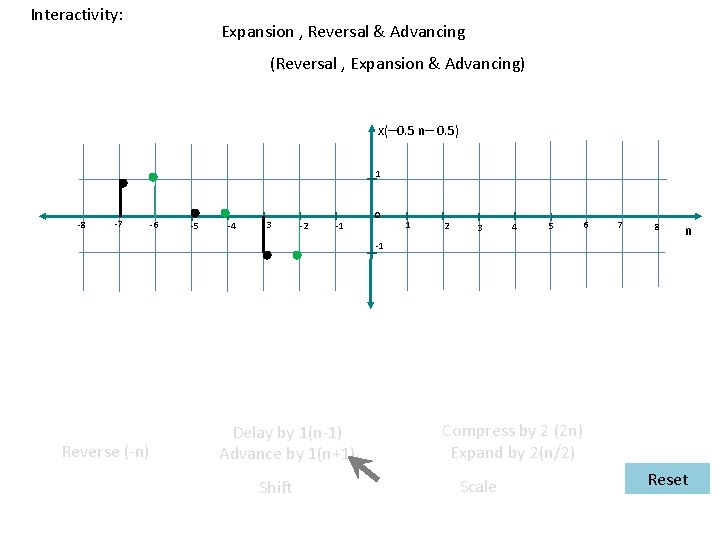
Interactivity: Reversal , Expansion & Advancing x( – 0. 5 n ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

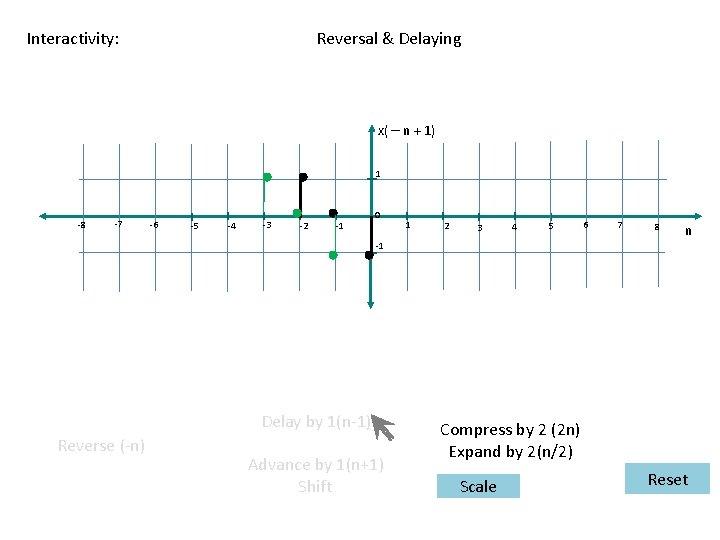
Interactivity: Reversal & Delaying x( – n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

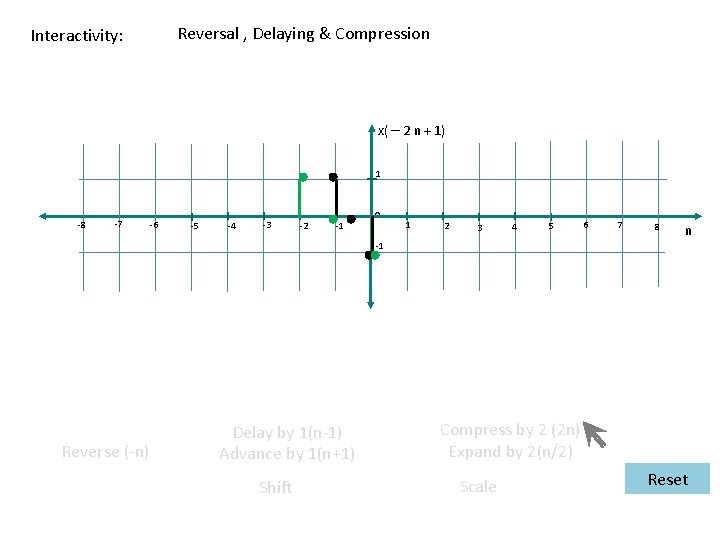
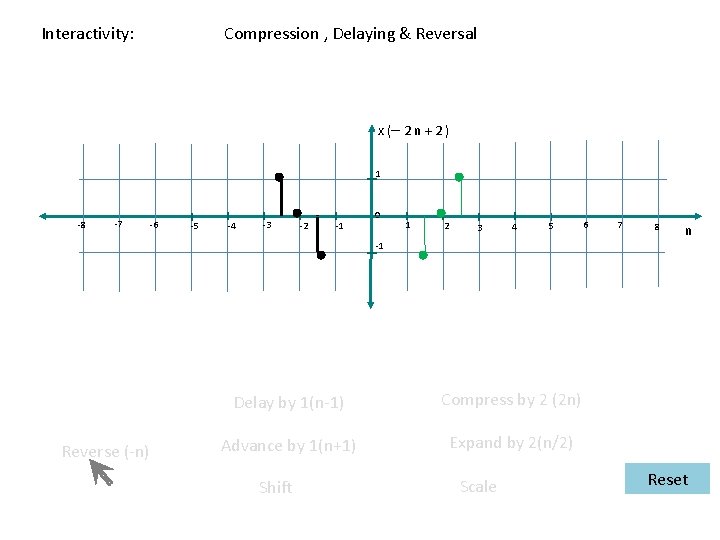
Reversal , Delaying & Compression Interactivity: x( – 2 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

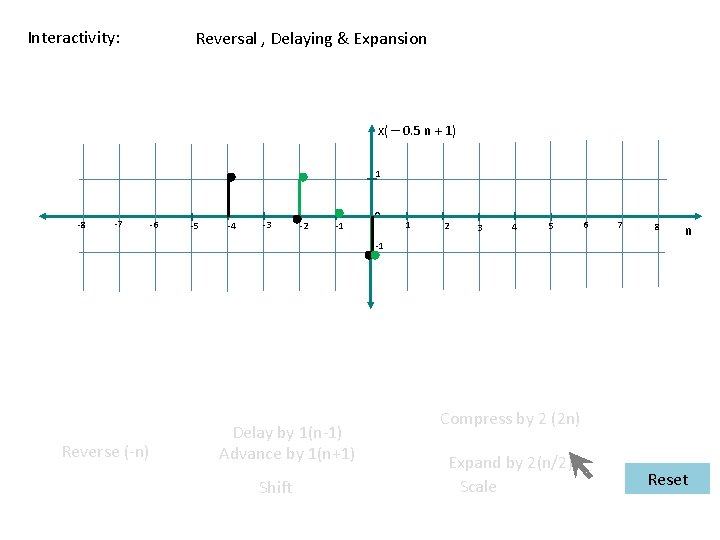
Interactivity: Reversal , Delaying & Expansion x( – 0. 5 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

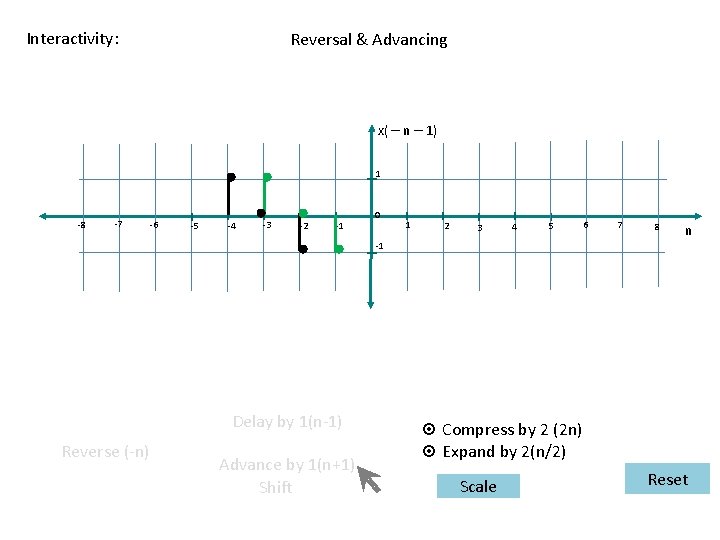
Interactivity: Reversal & Advancing x( – n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

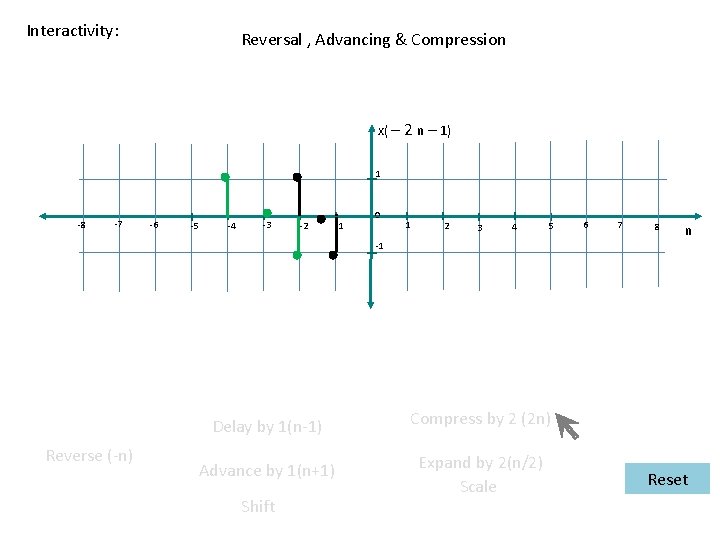
Interactivity: Reversal , Advancing & Compression x( – 2 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Scale Shift Reset

Interactivity: Reversal , Advancing & Expansion x( – 0. 5 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

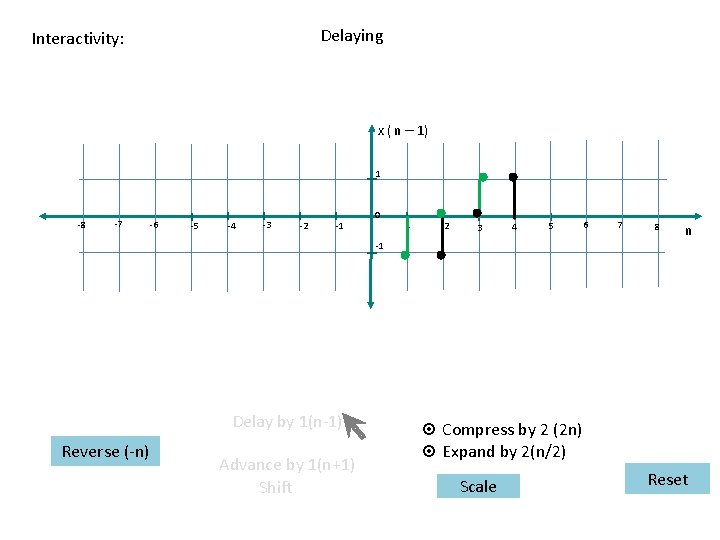
Delaying Interactivity: x ( n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

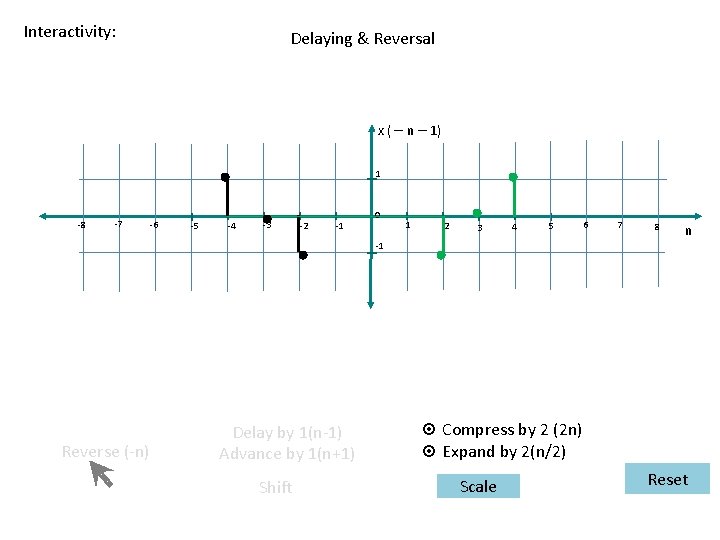
Interactivity: Delaying & Reversal x ( – n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

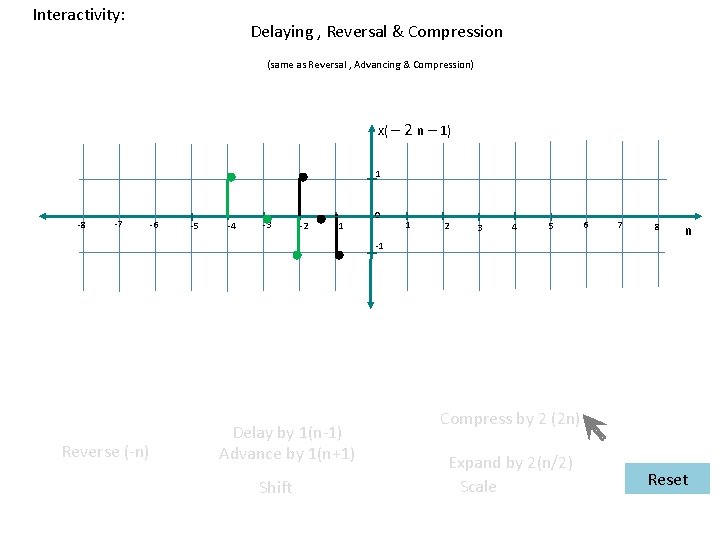
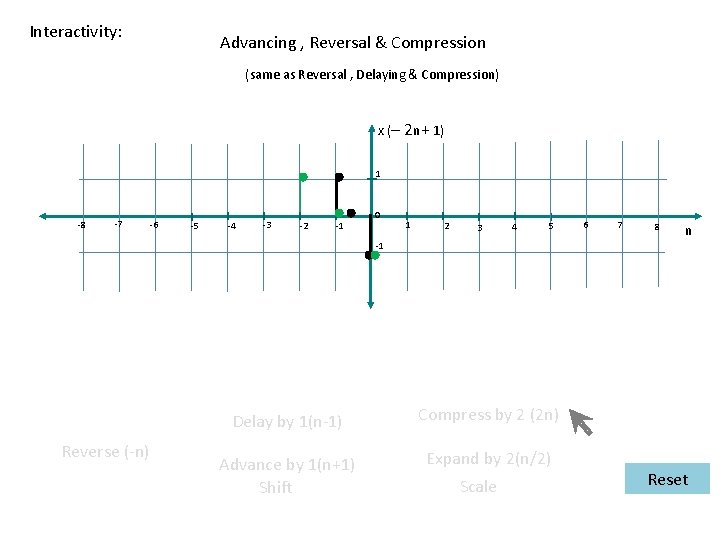
Interactivity: Delaying , Reversal & Compression (same as Reversal , Advancing & Compression) x( – 2 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

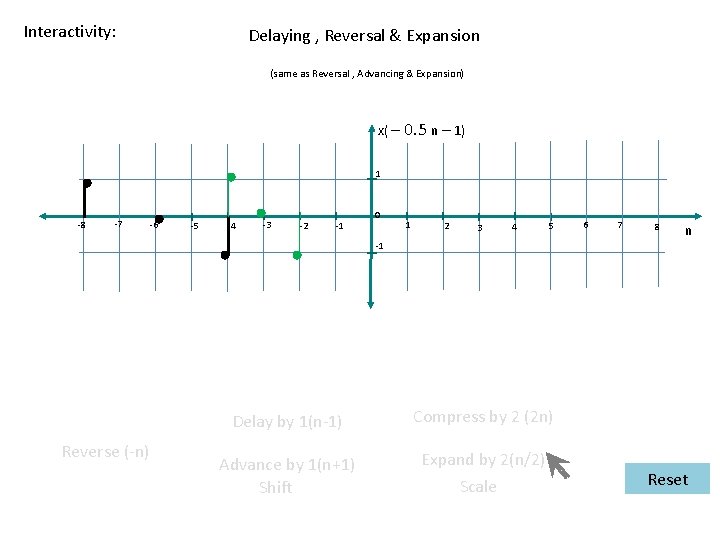
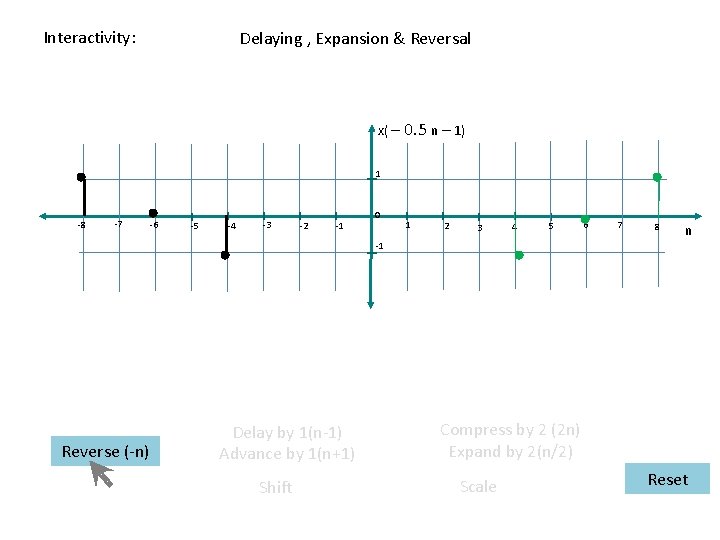
Interactivity: Delaying , Reversal & Expansion (same as Reversal , Advancing & Expansion) x( – 0. 5 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Shift Expand by 2(n/2) Scale Reset

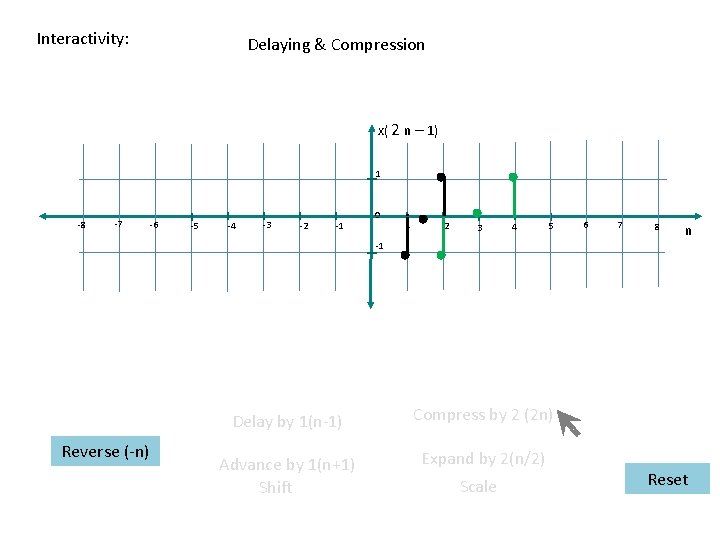
Interactivity: Delaying & Compression x( 2 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Shift Expand by 2(n/2) Scale Reset

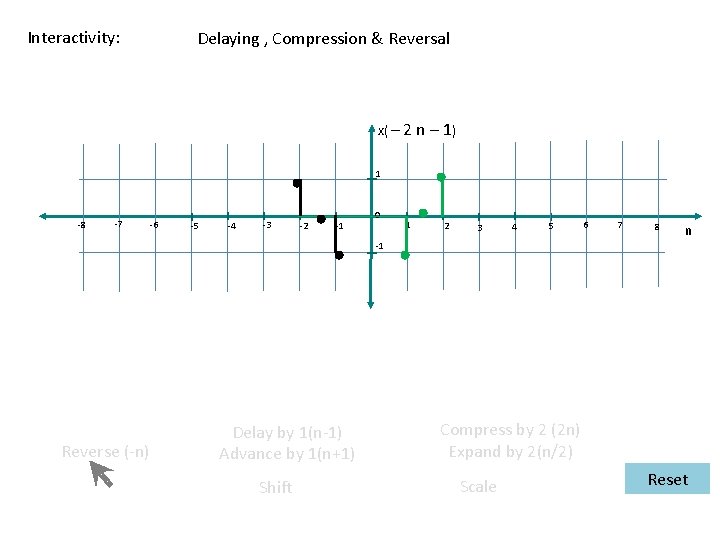
Interactivity: Delaying , Compression & Reversal x( – 2 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Delaying & Expansion Interactivity: x( 0. 5 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Delaying , Expansion & Reversal x( – 0. 5 n – 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

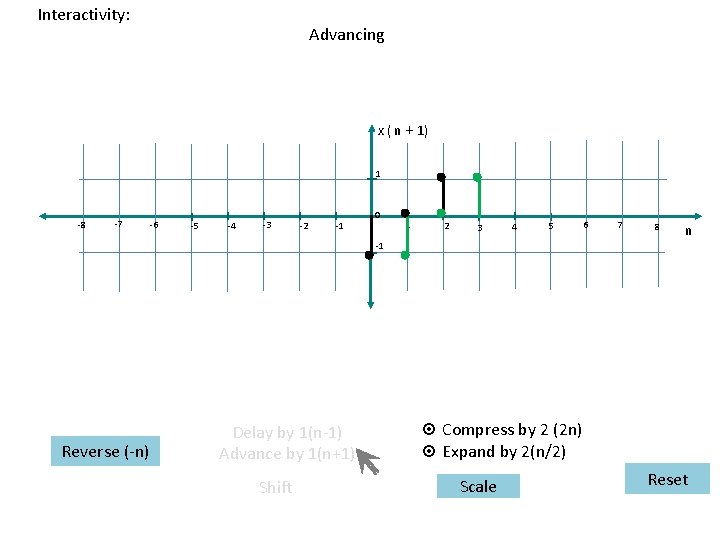
Interactivity: Advancing x ( n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

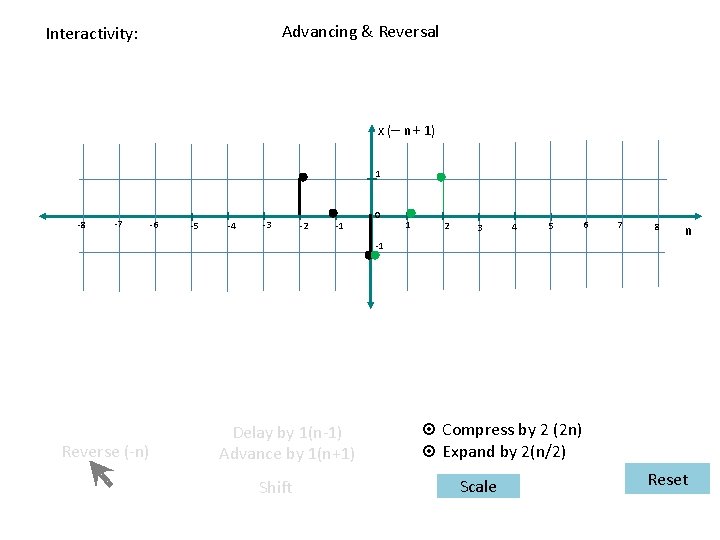
Advancing & Reversal Interactivity: x (– n+ 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift ¤ Compress by 2 (2 n) ¤ Expand by 2(n/2) Scale Reset

Interactivity: Advancing , Reversal & Compression (same as Reversal , Delaying & Compression) x (– 2 n+ 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Shift Expand by 2(n/2) Scale Reset

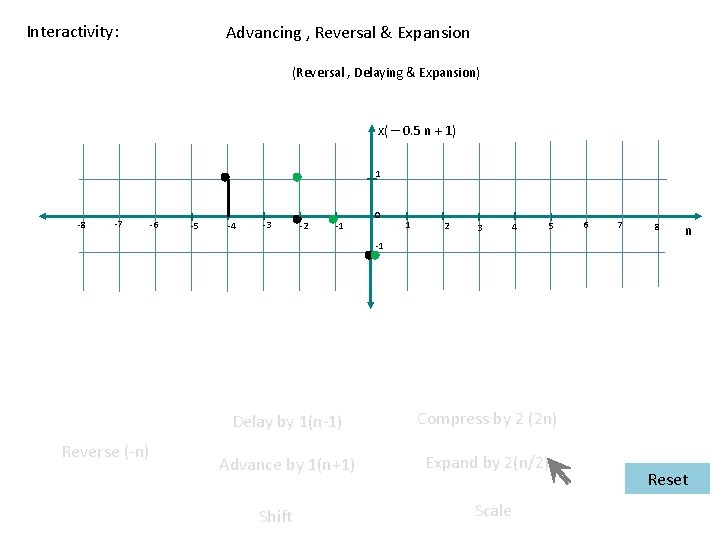
Interactivity: Advancing , Reversal & Expansion (Reversal , Delaying & Expansion) x( – 0. 5 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

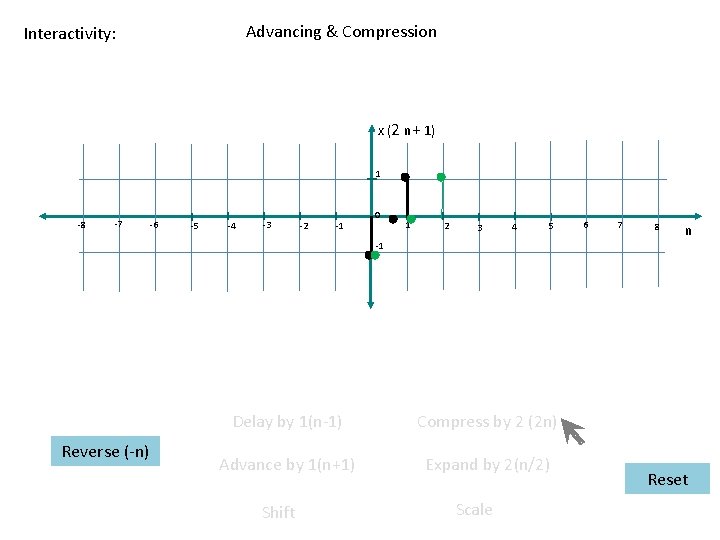
Advancing & Compression Interactivity: x (2 n+ 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

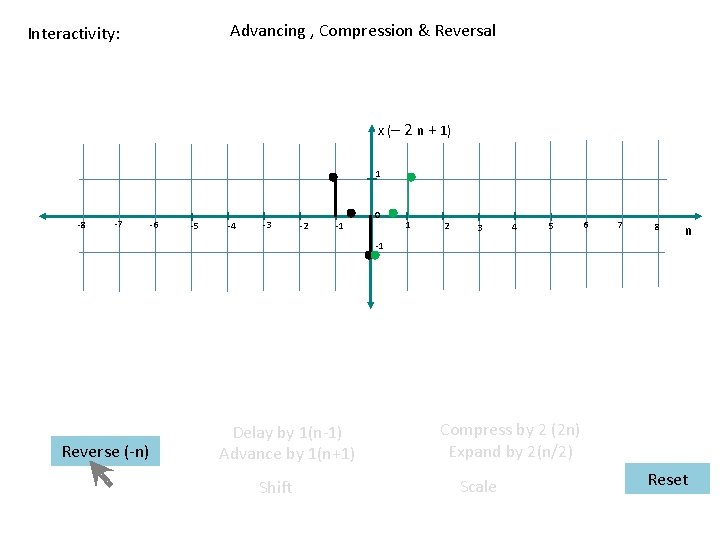
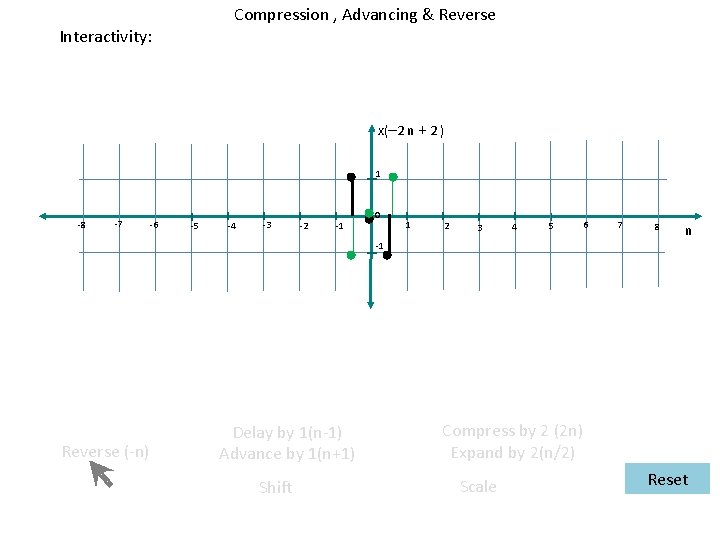
Advancing , Compression & Reversal Interactivity: x (– 2 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Advancing & Expansion x (0. 5 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

Advancing , Expansion & Reversal Interactivity: x (0. 5 n + 1) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Compression Interactivity: x(2 n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 ¤ Delay by 1(n-1) Reverse (-n) ¤ Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Compression & Reversal x( – 2 n ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

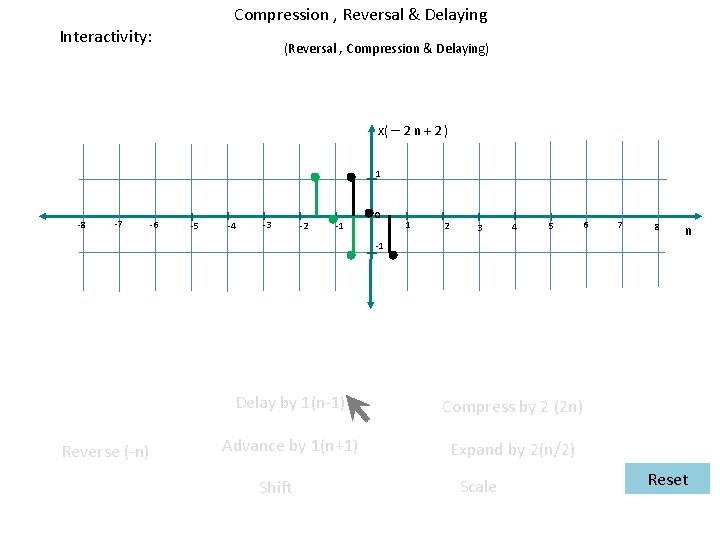
Compression , Reversal & Delaying Interactivity: (Reversal , Compression & Delaying) x( – 2 n + 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

Compression , Reversal & Advancing Interactivity: (Reversal , Compression & Advancing) x( – 2 n – 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2(2 n) Expand by 2(n/2) Reset Scale

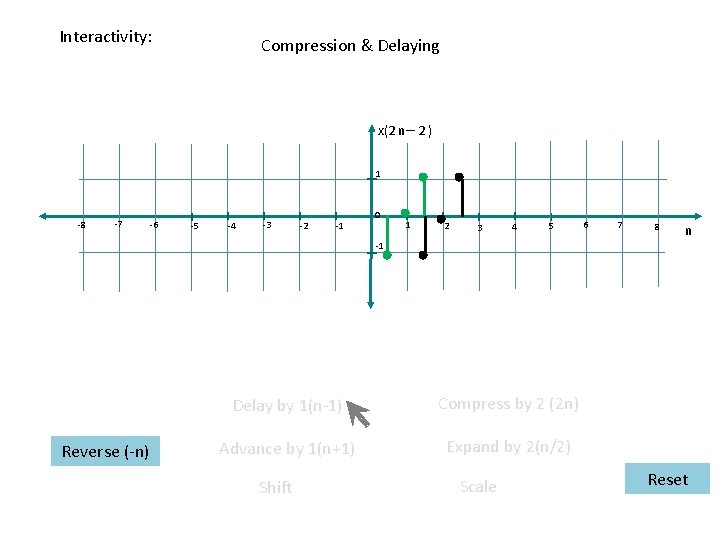
Interactivity: Compression & Delaying x(2 n– 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

Compression , Delaying & Reversal Interactivity: x (– 2 n + 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Expand by 2(n/2) Shift Scale Reset

Compression & Advancing Interactivity: x(2 n+ 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Delay by 1(n-1) Reverse (-n) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Compression , Advancing & Reverse Interactivity: x(– 2 n + 2 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

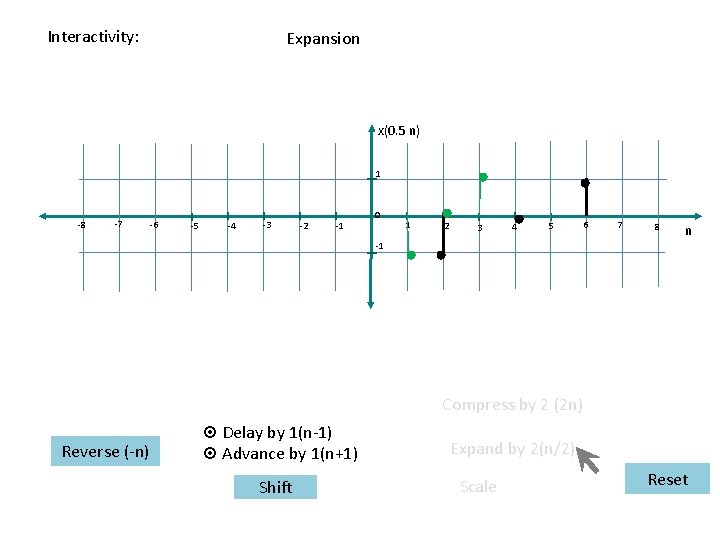
Interactivity: Expansion x(0. 5 n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Compress by 2 (2 n) Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift Expand by 2(n/2) Scale Reset

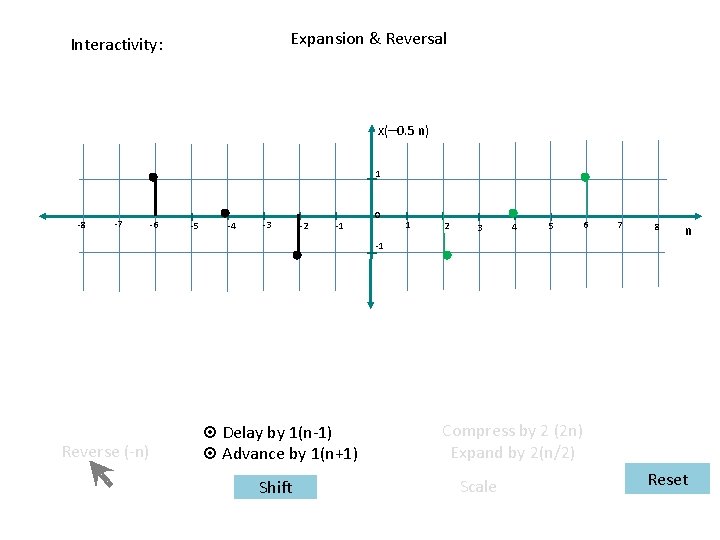
Expansion & Reversal Interactivity: x(– 0. 5 n) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) ¤ Delay by 1(n-1) ¤ Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Expansion , Reversal & Delaying (Reversal , Expansion & Delaying) x(– 0. 5 n + 0. 5) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Compress by 2 (2 n) Advance by 1(n+1) Shift Expand by 2(n/2) Scale Reset

Interactivity: Expansion , Reversal & Advancing (Reversal , Expansion & Advancing) x(– 0. 5 n– 0. 5) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

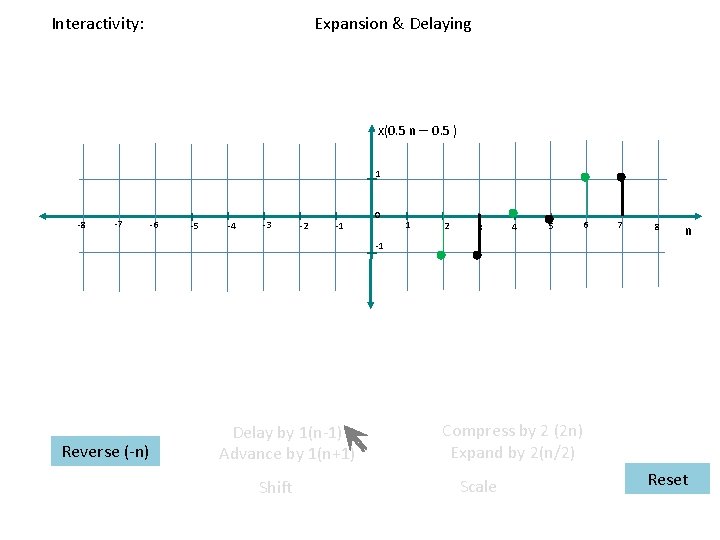
Interactivity: Expansion & Delaying x(0. 5 n – 0. 5 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

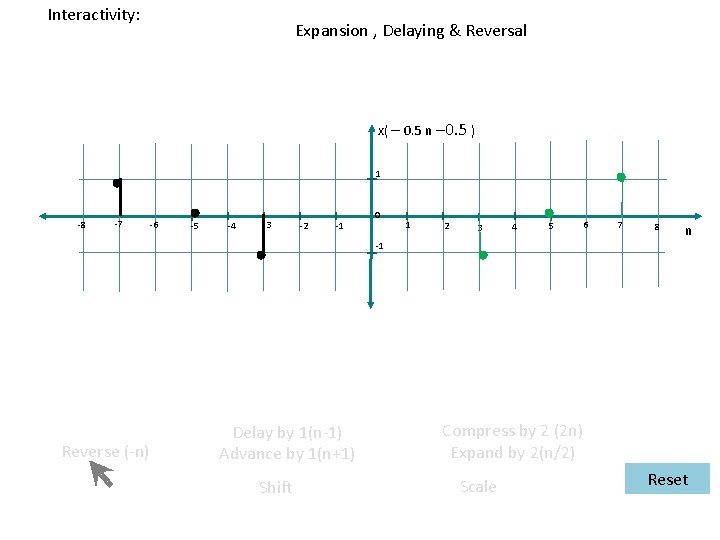
Interactivity: Expansion , Delaying & Reversal x( – 0. 5 n – 0. 5 ) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Expansion & Advancing x(0. 5 n + 0. 5) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

Interactivity: Expansion , Advancing & Reversal x (– 0. 5 n + 0. 5) 1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n -1 Reverse (-n) Delay by 1(n-1) Advance by 1(n+1) Shift Compress by 2 (2 n) Expand by 2(n/2) Scale Reset

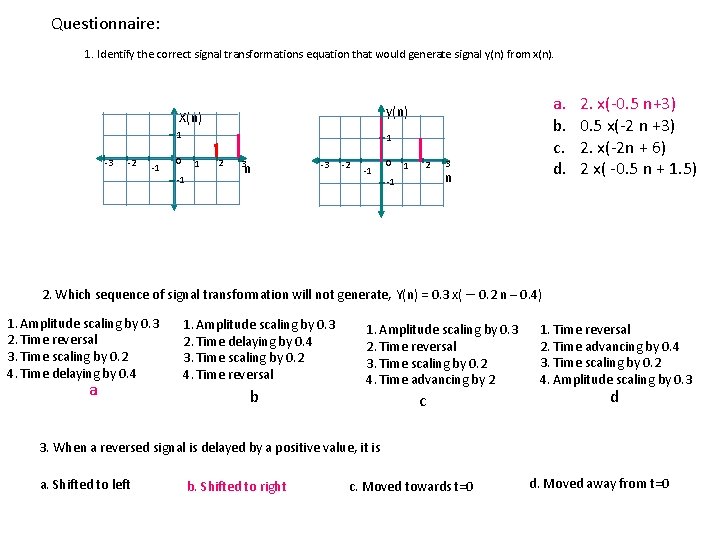
Questionnaire: 1. Identify the correct signal transformations equation that would generate signal y(n) from x(n). 1 -3 -2 -1 a. b. c. d. y(n) X(n) 1 0 1 -1 2 3 n -3 -2 -1 0 1 2 -1 3 n 2. x(-0. 5 n+3) 0. 5 x(-2 n +3) 2. x(-2 n + 6) 2 x( -0. 5 n + 1. 5) 2. Which sequence of signal transformation will not generate, Y(n) = 0. 3 x( – 0. 2 n – 0. 4) 1. Amplitude scaling by 0. 3 2. Time reversal 3. Time scaling by 0. 2 4. Time delaying by 0. 4 a 1. Amplitude scaling by 0. 3 2. Time delaying by 0. 4 3. Time scaling by 0. 2 4. Time reversal b 1. Amplitude scaling by 0. 3 2. Time reversal 3. Time scaling by 0. 2 4. Time advancing by 2 c 1. Time reversal 2. Time advancing by 0. 4 3. Time scaling by 0. 2 4. Amplitude scaling by 0. 3 d 3. When a reversed signal is delayed by a positive value, it is a. Shifted to left b. Shifted to right c. Moved towards t=0 d. Moved away from t=0

Glossary Signal: Any physical quantity that varies with time space, or any other variable. Signal Transformation: Arithmetic operations performed on signal amplitude or time that manipulate the signal. Shifting: The shifting of a signal in time. Delaying: Causing the signal to occur late (shift to right) by subtracting a positive constant from time parameter. Advancing: Causing the signal to occur early (shift to left) by adding a positive constant to time parameter. . Scaling: Compressing or expanding a signal by multiplying the time variable by some quantity. Compression: Narrowing the signal in time, by multiplying time parameter by a positive constant grater than 1. Expansion: Widening the signal in time, by multiplying time parameter by a positive constant lower than 1. Reversal: Flipping the signal over amplitude axis by multiplying time parameter by -1.

References John G. Proakis and Dimitris G. Manolakis, Digital Signal Processing: Principles, Algorithms, and Applications, Prentice Hall, 3 rd edition, 1996 M. H. Hayes, Digital Signal Processing, Mc. Graw Hill, 2007