TRANSFORMASI LINIER KANIA EVITA DEWI DEFINISI Suatu fungsi

TRANSFORMASI LINIER KANIA EVITA DEWI

DEFINISI Suatu fungsi yang memetakan suatu vektor di ruang vektor V ke ruang vektor W (dituliskan ) disebut sebagai transformasi linear bila berlaku :

Operasi linier • Jika V = W maka transformasi disebut operator linear pada V. Contoh:

Transformasi Matriks • Transformasi dengan disebut transformasi matriks, sedangkan A disebut matriks transformasi. Contoh:

Contoh • Tentukan standar matriks (matriks A) dari transformasi linier berikut.

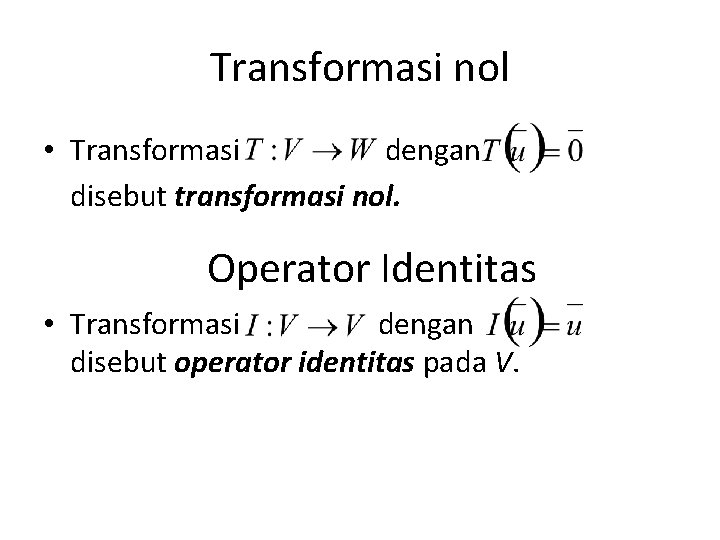
Transformasi nol • Transformasi dengan disebut transformasi nol. Operator Identitas • Transformasi dengan disebut operator identitas pada V.

Teorema 1 • Jika T: V→ W adalah sebuah transformasi linier, maka

Kernel dan Range • Diketahui transformasi linear T: V→W dengan 1. Kernel dari T, dinotasikan ker(T), didefinisikan 2. Range dari T, dinotasikan im(T), didefinisikan

Dimensi • Jika T: V→W adalah transformasi linier 1. Dimensi dari ker(T) disebut nulitas dari T, dinotasikan null(T). 2. Dimensi dari im(T) disebut rank dari T, dinotasikan rk (T).

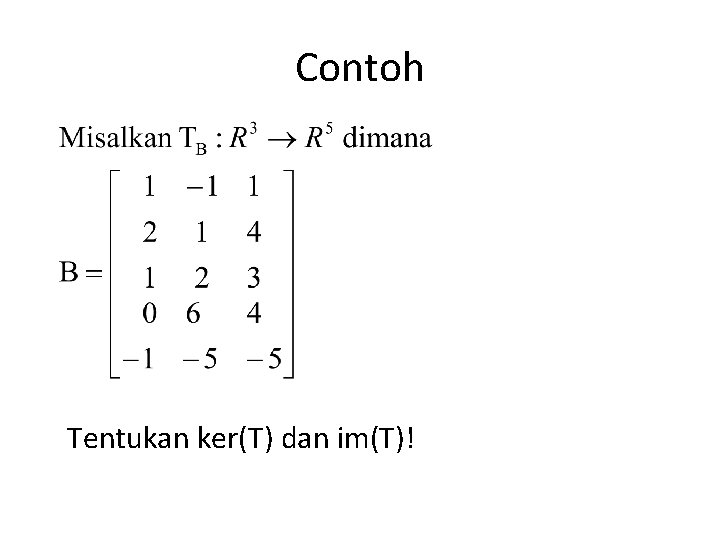
Teorema • Jika adalah transformasi linier dimana A adalah matriks m x n. Maka 1. ker(T) adalah himpunan penyelesaian dari 2. im(T) adalah ruang kolom dari matriks A 3. rk(T) = rk(A) 4. rk(T) + null (T) = n

Contoh Tentukan ker(T) dan im(T)!

Matriks Transformasi • Jika T: V→W adalah transformasi linier, B = {b 1, b 2, …, bn} adalah basis dari V dan C = {c 1, c 2, … cm} adalah basis dari W. Didefiniskan matriks m xn yaitu [T]B, C dengan [T]B, C = (aij) dimana j merupakan

Tentukan [T]B, C • T : F 3 → F 2 adalah transformasi linier yang didefinisikan

Tentukan [T]B, C • T : F 3 → F 2 adalah transformasi linier yang didefinisikan

Teorema 3 • Misal T : V→W adalah transformasi linier, Jika B adalah basis V dan C adalah basis W. Maka untuk setiap v Є V

Contoh • Jika U : R 2 → R 3 dengan 1. Tentukan [U]B, C 2. Jika Tentukan [U(x)]C

Matriks Transisi Matriks P = [I]B 1, B 2 disebut matriks transisi dari basis B 1 ke basis B 2. Definisi Keserupaan Misalkan A dan B adalah matriks m x n. Jika ada sebuah matriks P yang memiliki invers sehingga A = P B P-1, maka A serupa dengan B

Teorema 4 • Jika T: V→V adalah suatu linear pada suatu ruang vektor berdimensi terhingga. V , dan anggap B 1 dan B 2 adalah basis-basis untuk V. Maka Dimana P adalah matriks transisi dari B 2 ke B 1.

Contoh • Jika T: R 2→R 2 didefinisikan oleh 1. Tentukan matriks T yang berkenaan dengan basis standar B 1 ={e 1, e 2} 2. Jika dengan basis B 2 , tentukan matriks T berkenaan