Transformasi dan Model Warna Citra Digital Computer Vision

Transformasi dan Model Warna Citra Digital Computer Vision Materi 3 Eko Prasetyo Teknik Informatika UBHARA 2012

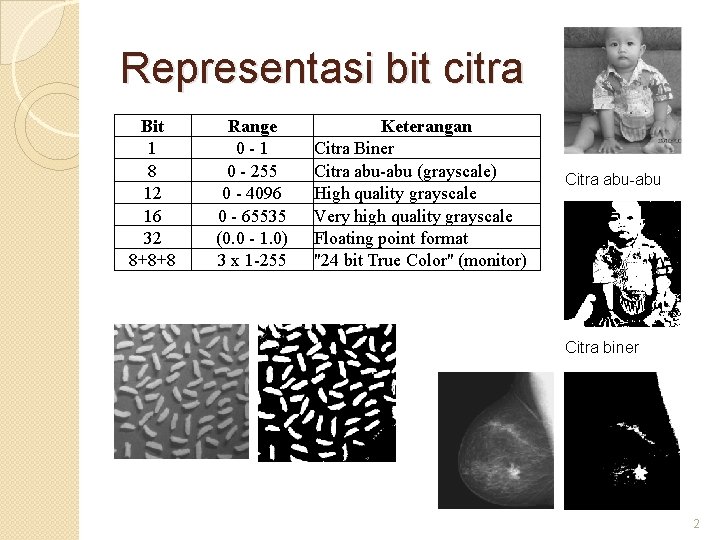
Representasi bit citra Bit 1 8 12 16 32 8+8+8 Range 0 -1 0 - 255 0 - 4096 0 - 65535 (0. 0 - 1. 0) 3 x 1 -255 Keterangan Citra Biner Citra abu-abu (grayscale) High quality grayscale Very high quality grayscale Floating point format "24 bit True Color" (monitor) Citra abu-abu Citra biner 2

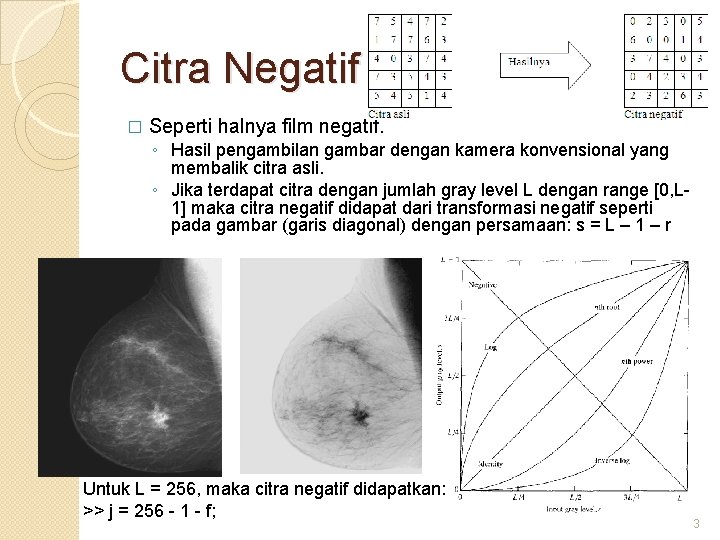
Citra Negatif � Seperti halnya film negatif. ◦ Hasil pengambilan gambar dengan kamera konvensional yang membalik citra asli. ◦ Jika terdapat citra dengan jumlah gray level L dengan range [0, L 1] maka citra negatif didapat dari transformasi negatif seperti pada gambar (garis diagonal) dengan persamaan: s = L – 1 – r Untuk L = 256, maka citra negatif didapatkan: >> j = 256 - 1 - f; 3

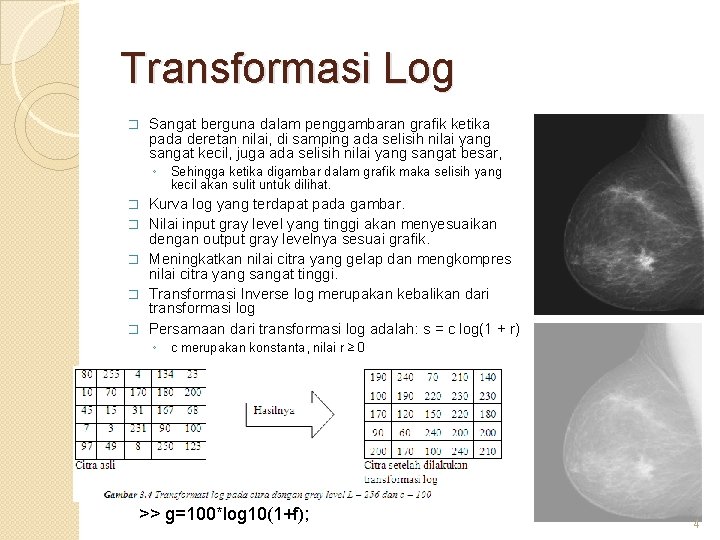
Transformasi Log � Sangat berguna dalam penggambaran grafik ketika pada deretan nilai, di samping ada selisih nilai yang sangat kecil, juga ada selisih nilai yang sangat besar, ◦ � � � Sehingga ketika digambar dalam grafik maka selisih yang kecil akan sulit untuk dilihat. Kurva log yang terdapat pada gambar. Nilai input gray level yang tinggi akan menyesuaikan dengan output gray levelnya sesuai grafik. Meningkatkan nilai citra yang gelap dan mengkompres nilai citra yang sangat tinggi. Transformasi Inverse log merupakan kebalikan dari transformasi log Persamaan dari transformasi log adalah: s = c log(1 + r) ◦ c merupakan konstanta, nilai r ≥ 0 >> g=100*log 10(1+f); 4

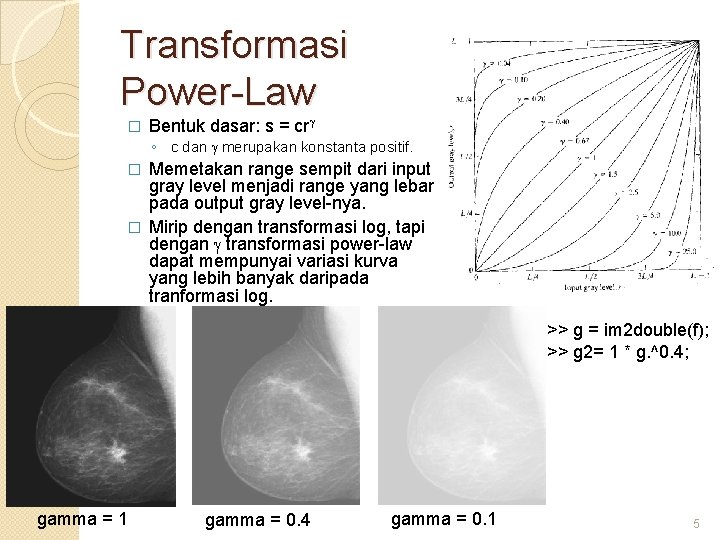
Transformasi Power-Law � Bentuk dasar: s = cr ◦ c dan merupakan konstanta positif. Memetakan range sempit dari input gray level menjadi range yang lebar pada output gray level-nya. � Mirip dengan transformasi log, tapi dengan transformasi power-law dapat mempunyai variasi kurva yang lebih banyak daripada tranformasi log. � >> g = im 2 double(f); >> g 2= 1 * g. ^0. 4; gamma = 1 gamma = 0. 4 gamma = 0. 1 5

Histogram � Histogram adalah dasar dari sejumlah teknik pemrosesan citra pada domain spasial, seperti perbaikan, kompresi dan segmentasi citra. � Histogram dari suatu citra digital dengan range tingkat [0…L-1] adalah sebuah fungsi diskrit h(rk)=nk ◦ rk adalah tingkat keabuan ke-k ◦ nk adalah jumlah piksel dalam citra yang memiliki tingkat keabuan rk. � Normalisasi histrogram dilakukan dengan membagi setiap nilai nk dengan total jumlah piksel dalam citra, yang dinyatakan dengan n. ◦ Histogram yang sudah dinormalisasi dinyatakan dengan p(rk)= nk/n, untuk k=0, 1, …, L-1. � p(rk) menyatakan estimasi probabilitas kemunculan tingkat keabuan rk. � Jumlah dari semua komponen “normalized histogram” sama dengan 1. 6

Histogram Sumbu horisontal dari histogram menyatakan nilai tingkat keabuan rk. � Sumbu vertikal menyatakan nilai dari h(rk)=nk atau p(rk) = nk/n (jika nilainya dinormalisasi). � >> figure, imshow(f); � >> figure, imhist(f); � 7 6 5 4 Jumlah piksel 3 2 1 0 1 -1 2 -1 3 -1 4 -1 5 -1 6 -1 7 -1 8 -1 Lever keabuan 7

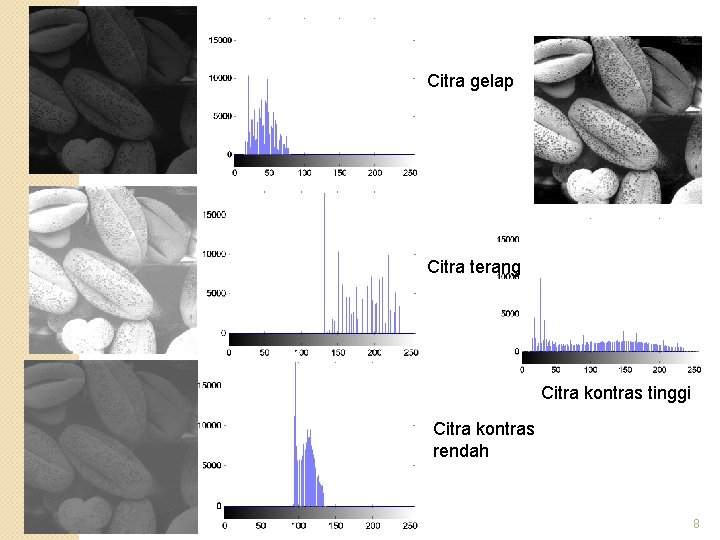
Citra gelap Citra terang Citra kontras tinggi Citra kontras rendah 8

Histogram Normalization �Menskalakan nilai piksel secara linear untuk menggunakan secara penuh jangkauan yang gray-scale yang tersedia. �Transformasi yang digunakan: untuk k=0, 1, 2, …, L-1 disebut “histogram normalization”. 9

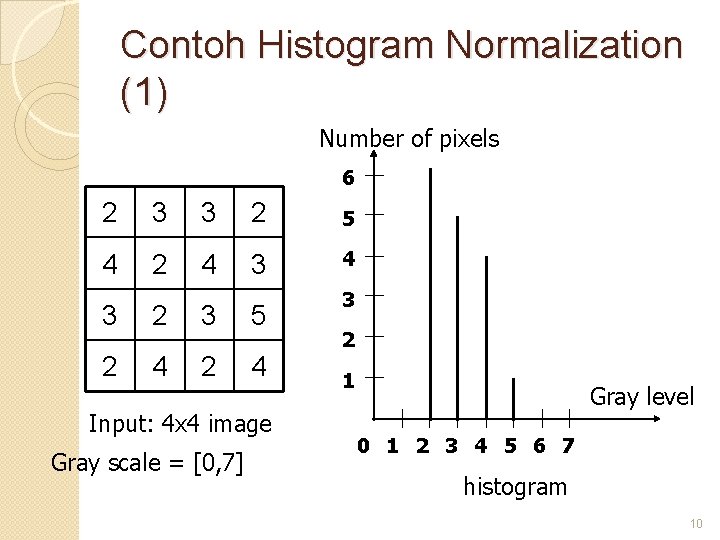
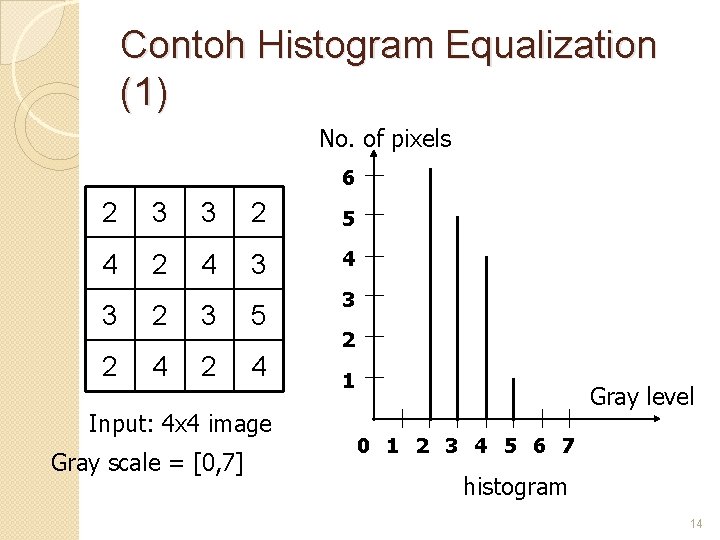
Contoh Histogram Normalization (1) Number of pixels 6 2 3 3 2 5 4 2 4 3 2 3 5 2 4 Input: 4 x 4 image Gray scale = [0, 7] 3 2 1 Gray level 0 1 2 3 4 5 6 7 histogram 10

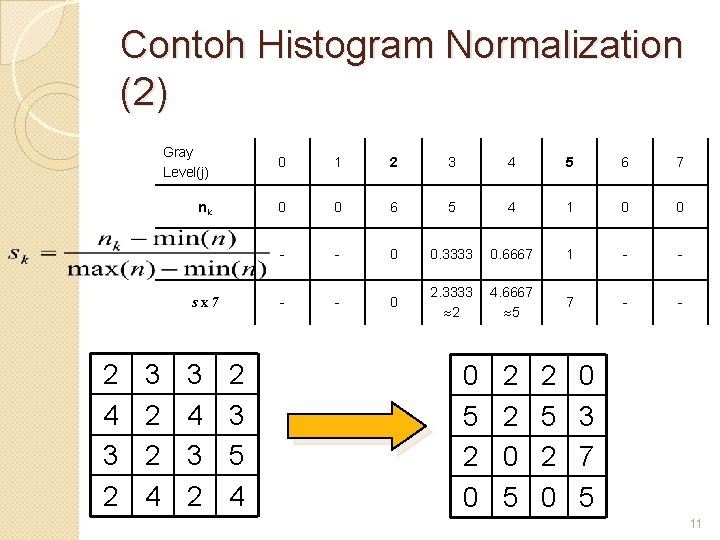
Contoh Histogram Normalization (2) Gray Level(j) 0 1 2 3 4 5 6 7 nk 0 0 6 5 4 1 0 0 - - 0 0. 3333 0. 6667 1 - - 0 2. 3333 2 4. 6667 5 7 - - sx 7 2 4 3 2 2 3 5 4 0 5 2 0 2 2 0 5 2 0 0 3 7 5 11

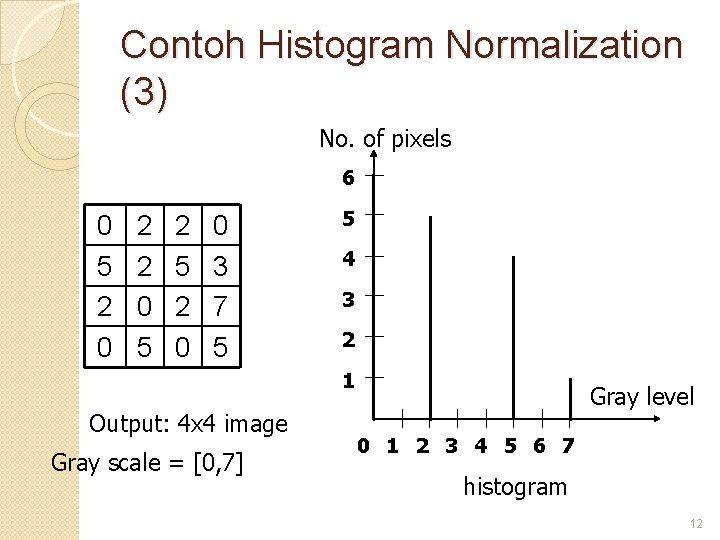
Contoh Histogram Normalization (3) No. of pixels 6 0 5 2 0 2 2 0 5 2 0 0 3 7 5 5 4 3 2 1 Output: 4 x 4 image Gray scale = [0, 7] Gray level 0 1 2 3 4 5 6 7 histogram 12

Histogram Equalization Histogram equalization digunakan untuk memetakan kembali nilai piksel untuk membuat perkiraan linear akumulasi histogram. � Transformasi yang digunakan: � untuk k=0, 1, 2, …, L-1 disebut “histogram equalization” atau “histogram linearization”. � Fungsi yang digunakan : � h = histeq(f, b) ◦ h merupakan citra hasil equalisasi, ◦ f merupakan variabel citra dan b adalah jumlah bins yang digunakan dalam membentuk histogram. nilai default, b=64 pada citra 6 bit. 13

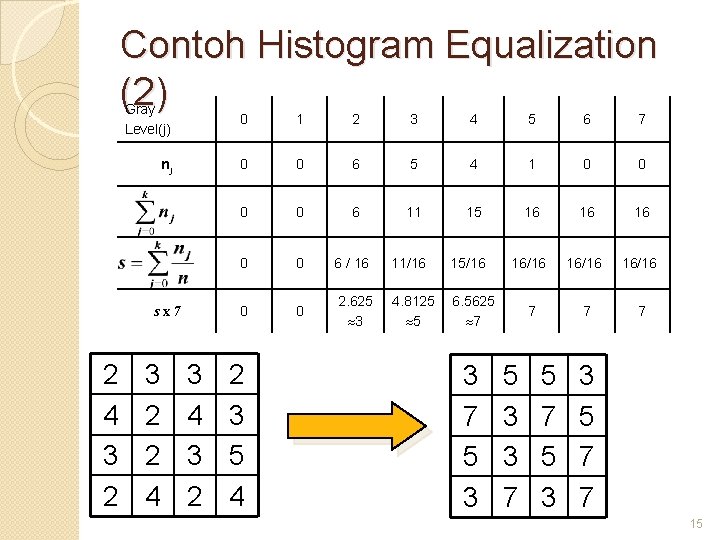
Contoh Histogram Equalization (1) No. of pixels 6 2 3 3 2 5 4 2 4 3 2 3 5 2 4 Input: 4 x 4 image Gray scale = [0, 7] 3 2 1 Gray level 0 1 2 3 4 5 6 7 histogram 14

Contoh Histogram Equalization (2) Gray Level(j) 0 1 2 3 4 5 6 7 nj 0 0 6 5 4 1 0 0 6 11 15 16 16 16 0 0 6 / 16 11/16 15/16 16/16 0 0 2. 625 3 4. 8125 5 6. 5625 7 7 sx 7 2 4 3 2 2 3 5 4 3 7 5 3 3 5 7 7 15

Contoh Histogram Equalization (3) No. of pixels 6 3 7 5 3 3 5 7 7 Output: 4 x 4 image Gray scale = [0, 7] 5 4 3 2 1 Gray level 0 1 2 3 4 5 6 7 histogram 16

Contoh Histogram Equalization (4) � >> g = histeq(f, 256); sebelum sesudah 17

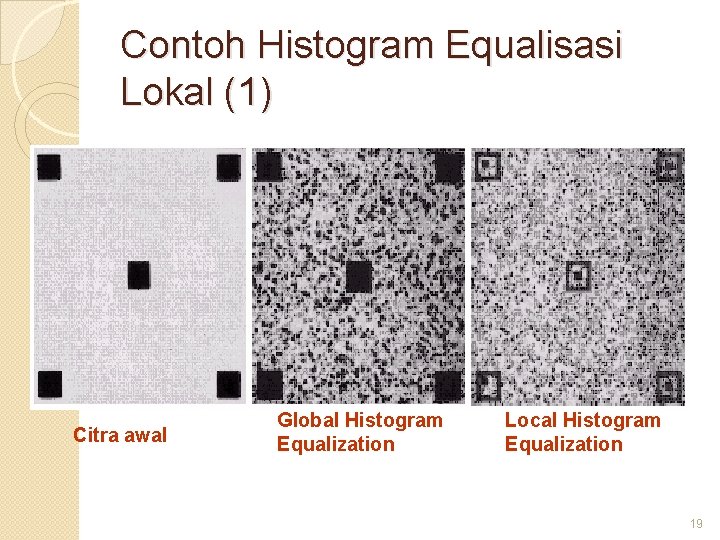
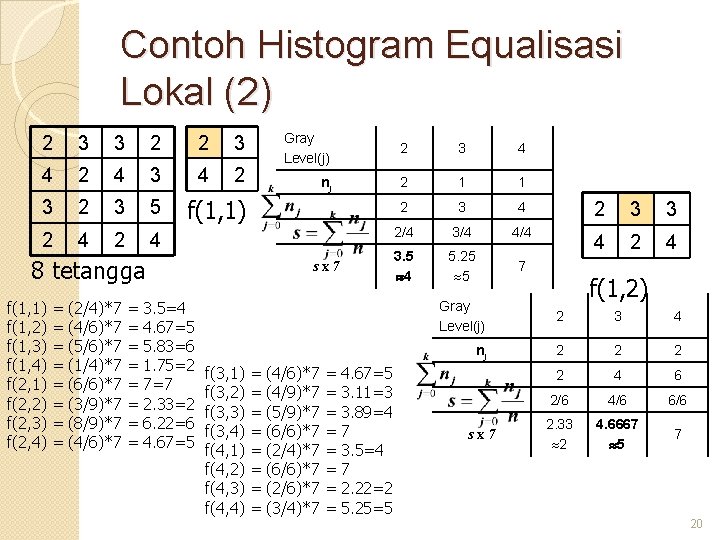
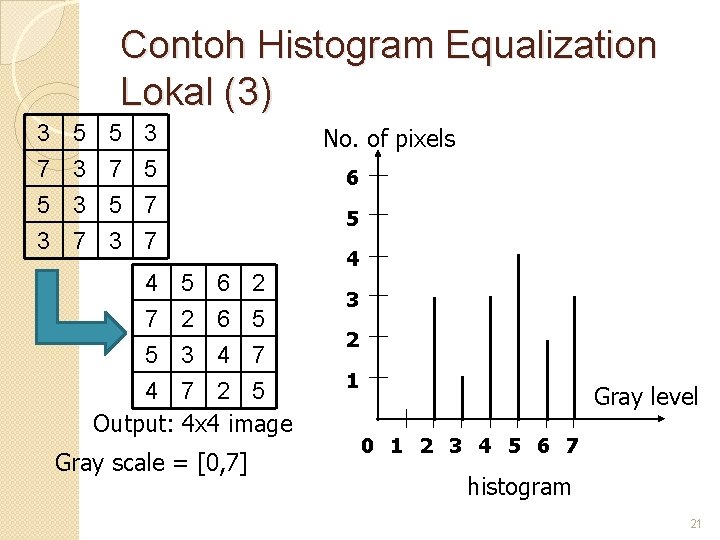
Histogram Equalisasi Lokal � Metode pemrosesan histogram yang sudah dibahas, yaitu “histogram equalization” bersifat global, karena piksel-piksel dimodifikasi menggunakan fungsi transformasi berbasis pada intensitas seluruh piksel pada citra. � Kadang diperlukan perbaikan pada suatu daerah yang kecil di dalam citra. 1 2 Teknik “histogram equalization” dapat diterapkan untuk perbaikan lokal. � Caranya: 3 4 5 6 7 8 9 � 8 tetangga 1. Definisikan daerah ketetanggaan (neighborhood) 2. Pada setiap lokasi piksel, histogram dari piksel-piksel dalam neighborhood dihitung. 3. Tentukan fungsi transformasi “histogram equalization” dan fungsi ini digunakan untuk memetakan intensitas piksel pada pusat neighborhood. 4. Ulangi langkah 2– 3 untuk seluruh piksel dalam citra. 18

Contoh Histogram Equalisasi Lokal (1) Citra awal Global Histogram Equalization Local Histogram Equalization 19

Contoh Histogram Equalisasi Lokal (2) 2 3 3 2 2 3 4 2 4 3 4 2 3 5 2 4 = = = = (2/4)*7 (4/6)*7 (5/6)*7 (1/4)*7 (6/6)*7 (3/9)*7 (8/9)*7 (4/6)*7 = = = = 2 3 4 nj 2 1 1 2 3 4 2 3 3 2/4 3/4 4/4 3. 5 4 5. 25 5 4 2 4 7 f(1, 1) 8 tetangga f(1, 1) f(1, 2) f(1, 3) f(1, 4) f(2, 1) f(2, 2) f(2, 3) f(2, 4) Gray Level(j) 3. 5=4 4. 67=5 5. 83=6 1. 75=2 7=7 2. 33=2 6. 22=6 4. 67=5 sx 7 f(3, 1) f(3, 2) f(3, 3) f(3, 4) f(4, 1) f(4, 2) f(4, 3) f(4, 4) = = = = (4/6)*7 (4/9)*7 (5/9)*7 (6/6)*7 (2/4)*7 (6/6)*7 (2/6)*7 (3/4)*7 = = = = 4. 67=5 3. 11=3 3. 89=4 7 3. 5=4 7 2. 22=2 5. 25=5 f(1, 2) Gray Level(j) 2 3 4 nj 2 2 4 6 2/6 4/6 6/6 2. 33 2 4. 6667 5 7 sx 7 20

Contoh Histogram Equalization Lokal (3) 3 7 5 3 3 5 7 7 4 5 6 2 7 2 6 5 5 3 4 7 2 5 Output: 4 x 4 image Gray scale = [0, 7] No. of pixels 6 5 4 3 2 1 Gray level 0 1 2 3 4 5 6 7 histogram 21

Citra Biner � Citra yang hanya mempunyai nilai level intensitas keabuan hitam dan putih (0 dan 1). � Menjadi dasar dalam pengolahan citra: morfologi, segmentasi, representasi, pengenalan pola, dsb. � Formula: ◦ Piksel yang diberi nilai 1 berkaitan dengan obyek sedangkan piksel yang diberi nilai 0 berkaitan dengan background. ◦ Ketika T adalah konstanta, pendekatan ini disebut global thresholding. 22

Thresholding � Salah satu cara memilih thresholding adalah dengan pemeriksaan visual histogram citra. � Histogram dalam gambar secara jelas mempunyai dua mode yang berbeda. ◦ Mudah untuk memilih threshold T yang membaginya. � Metode yang lain dalam pemilihan T adalah dengan trial and error, mengambil beberapa threshold berbeda sampai satu nilai T yang memberikan hasil yang baik sebagai keputusan yang ditemukan observer. 23

Thresholding (2) � Prosedur 1. 2. 3. 4. 5. untuk pemilihan threshold secara otomatis: Memilih perkiraan awal T. Disarankan perkiraan awal adalah titik tengah antara nilai intensitas minimum dan maksimum dalam citra. Mensegmentasi citra menggunakan T. Ini akan menghasilkan dua kelompok piksel: G 1, yang berisi semua piksel dengan nilai intensitas ≥ T, dan G 2, yang berisi semua piksel dengan nilai intensitas < T. Menghitung rata-rata nilai intensitas 1 dan 2 untuk piksel-piksel dalam region G 1 dan G 2. Menghitung nilai threshold yang baru: Mengulangi langkah 2 sampai 4 sampai perbedaan T dalam iterasi yang berturut-turut lebih kecil daripada parameter To sebelumnya. 24

Formulasi Otsu � Normalisasi histogram sebagai fungsi probability discrete density, sebagai: � ◦ di mana n adalah total jumlah piksel dalam citra, n q adalah jumlah piksel yang dipunyai level intensitas rq, dan L adalah total jumlah level intensitas yang tersedia dalam citra. Andaikan bahwa threshold k dipilih maka C 0 adalah sekumpulan piksel dengan level [0, 1, …, k – 1] dan C 1 adalah sekumpulan piksel dengan level [k, k + 1, …, L – 1]. � Metode Otsu memilih nilai k yang memaksimalkan between-class variance 2 B, yang didefinisikan sebagai: � >> T = graythresh(f) >> T = 0. 5*(double(min(i(: ))) + double(max(i(: )))); >> done = false; >> while ~done g = i >= T; Tnext = 0. 5*(mean(i(g)) + mean(i(~g))); done = abs(T - Tnext) < 0. 5; T = Tnext; end 25

Citra abu-abu ke biner � � � >> f = imread('anak. png'); >> T = graythresh(f) T= 0. 5529 >> g = im 2 bw(f, T); >> imwrite(g, 'anak_biner. tif'); >> f = imread('rice. tif'); >> T = graythresh(f) T= 0. 5255 >> g = im 2 bw(f, T); >> imwrite(g, 'rice_biner. tif'); Citra abu-abu Citra biner 26

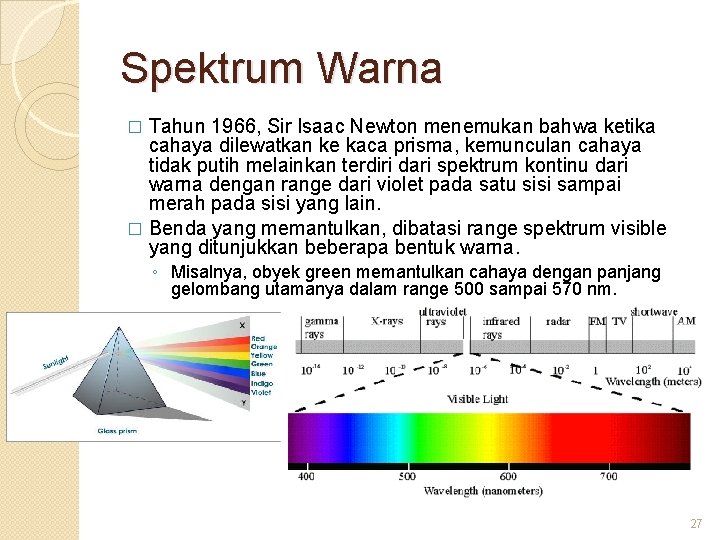
Spektrum Warna Tahun 1966, Sir Isaac Newton menemukan bahwa ketika cahaya dilewatkan ke kaca prisma, kemunculan cahaya tidak putih melainkan terdiri dari spektrum kontinu dari warna dengan range dari violet pada satu sisi sampai merah pada sisi yang lain. � Benda yang memantulkan, dibatasi range spektrum visible yang ditunjukkan beberapa bentuk warna. � ◦ Misalnya, obyek green memantulkan cahaya dengan panjang gelombang utamanya dalam range 500 sampai 570 nm. 27

Kuantitas dasar warna Cahaya kromatis merentangkan spektrum elektromagnetik mulai dari kira-kira 400 sampai 700 nm. � Tiga kuantitas dasar: radiance, luminance, dan brightness. � Radiance adalah jumlah perkiraan energi yang mengalir dari sumber cahaya, dan biasanya diukur dalam watts (W). � Luminance diukur dalam lumens (lm), memberikan ukuran perkiraan energi yang dilihat observer dari sumber cahaya. � ◦ Misalnya, cahaya diemisikan dari operasi sumber dalam jarak region infrared dari spektrum yang dapat mempunyai energi yang signifikan (radiance), tetapi observer akan kesulitan melihatnya; luminasinya hampir menjadi nol. � Brightness adalah deskriptor subyektif yang secara praktek tidak mungkin diukur. 28

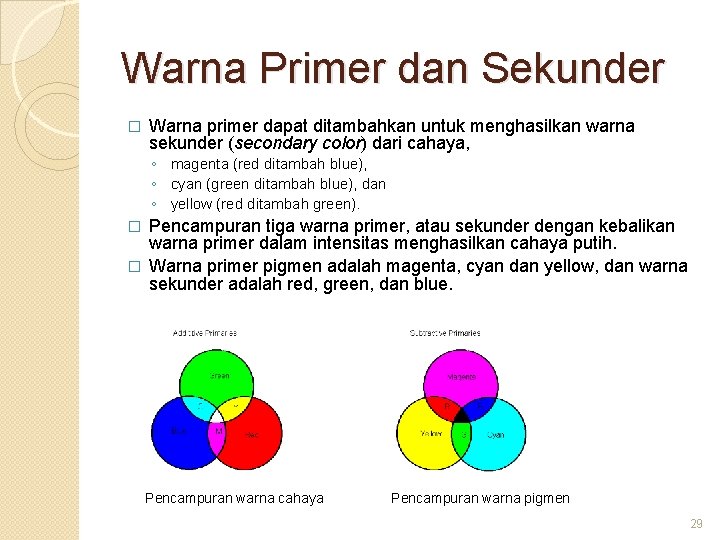
Warna Primer dan Sekunder � Warna primer dapat ditambahkan untuk menghasilkan warna sekunder (secondary color) dari cahaya, ◦ magenta (red ditambah blue), ◦ cyan (green ditambah blue), dan ◦ yellow (red ditambah green). Pencampuran tiga warna primer, atau sekunder dengan kebalikan warna primer dalam intensitas menghasilkan cahaya putih. � Warna primer pigmen adalah magenta, cyan dan yellow, dan warna sekunder adalah red, green, dan blue. � Pencampuran warna cahaya Pencampuran warna pigmen 29

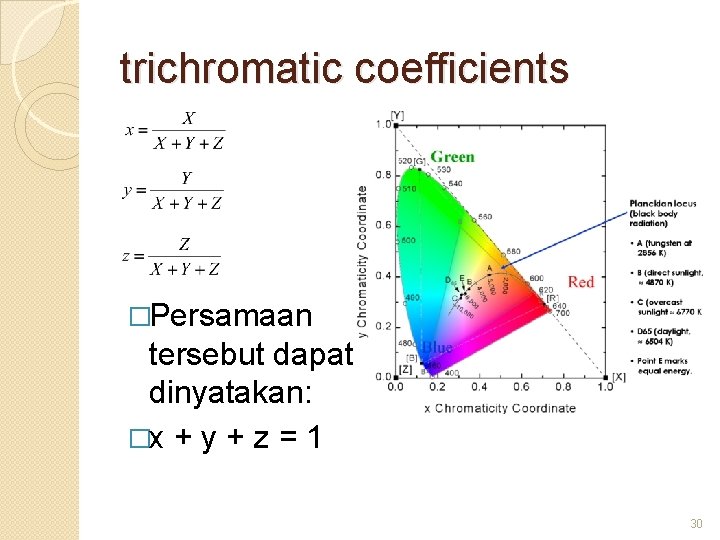
trichromatic coefficients �Persamaan tersebut dapat dinyatakan: �x + y + z = 1 30

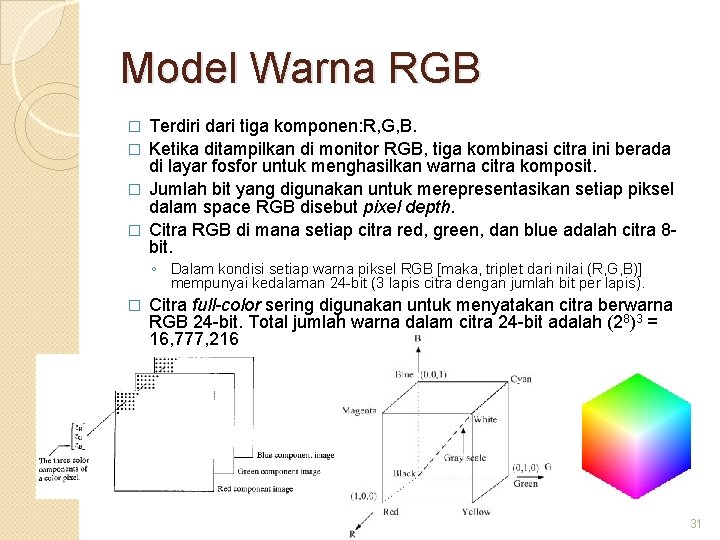
Model Warna RGB Terdiri dari tiga komponen: R, G, B. � Ketika ditampilkan di monitor RGB, tiga kombinasi citra ini berada di layar fosfor untuk menghasilkan warna citra komposit. � Jumlah bit yang digunakan untuk merepresentasikan setiap piksel dalam space RGB disebut pixel depth. � Citra RGB di mana setiap citra red, green, dan blue adalah citra 8 bit. � ◦ Dalam kondisi setiap warna piksel RGB [maka, triplet dari nilai (R, G, B)] mempunyai kedalaman 24 -bit (3 lapis citra dengan jumlah bit per lapis). � Citra full-color sering digunakan untuk menyatakan citra berwarna RGB 24 -bit. Total jumlah warna dalam citra 24 -bit adalah (28)3 = 16, 777, 216 31

Citra RGB >> i = imread('city_bridge. jpg'); >> f. R = i(: , 1); >> f. G = i(: , 2); >> f. B = i(: , 3); Citra RGB Komponen Red Komponen Green Komponen Blue >> rgb_image = cat(3, f. R, f. G, f. B) 32

Model Warna CMY dan CMYK (Cyan, Magenta, Yellow, Black) Perangkat yang menyimpan pigmen berwarna pada kertas, seperti printer dan mesin fotokopi berwarna, membutuhkan data input CMY (konversi RGB ke CMY secara internal). � Konversi (persamaan dibawah): � ◦ Asumsi bahwa semua nilai warna dinormalisasi dalam range [0, 1]. Persamaan di atas menunjukan bahwa cahaya dipantulkan dari permukaan yang dilapisi dengan cyan murni tidak berisi red (karena C = 1 – R dalam persamaannya). � Pengolahan citra dengan model warna ini digunakan dalam hubungan dengan pembuatan output hardcopy. � Kombinasi tiga warna ini untuk pencetakan menghasilkan warna yang tidak sepenuhnya hitam � ◦ Untuk menghasilkan warna hitam yang benar (biasanya lebih dominan dalam pencetakan), warna keempat, black ditambahkan, memberikan kemunculan model warna CMYK >> i. CMY = imcomplement(i. RGB); Citra RGB Citra CMY 33

Model Warna HSI Sistem RGB cocok dengan kenyataan bahwa mata manusia dengan kuat dapat mengetahui warna primer red, green, dan blue. � Sayangnya, RGB, CMY, dan model warna sejenis tidak secara baik cocok untuk menggambarkan warna dalam prakteknya untuk interpretasi manusia. � ◦ Misalnya, tidak mereferensikan ke warna dari automobile dengan pemberian persentase dari setiap warna primer yang mengisi warnanya. ◦ Jangan dianggap bahwa citra berwarna terdiri dari tiga citra primer yang dikombinasikan untuk membentuk citra tunggal. Model warna HSI (hue, saturation, intensity), memisahkan komponen intensitas dari informasi warna yang dibawa (hue dan saturasi) dalam warna citra. � Model HSI adalah tool yang ideal untuk mengembangkan algoritma pengolahan citra berdasarkan pada deskripsi warna yang alami dan intuitif terhadap manusia, pengembang dan usernya. � 34

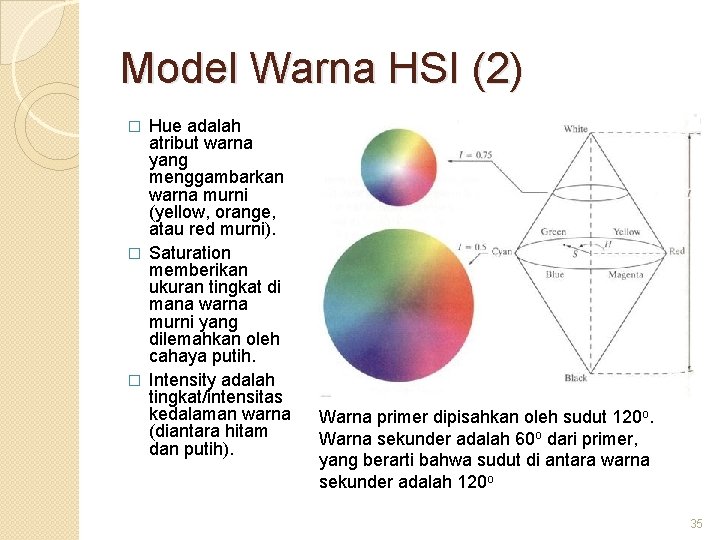
Model Warna HSI (2) Hue adalah atribut warna yang menggambarkan warna murni (yellow, orange, atau red murni). � Saturation memberikan ukuran tingkat di mana warna murni yang dilemahkan oleh cahaya putih. � Intensity adalah tingkat/intensitas kedalaman warna (diantara hitam dan putih). � Warna primer dipisahkan oleh sudut 120 o. Warna sekunder adalah 60 o dari primer, yang berarti bahwa sudut di antara warna sekunder adalah 120 o 35

Model Warna HSI (3) Citra RGB Citra Hue Citra HSI Citra Saturation Citra Intensity/Gray 36

Konversi warna RGB ke HSI Hue Intensity / Gray Saturation 37

Konversi warna HSI ke RGB Jika diberikan nilai HSI dalam interval [0, 1] maka dapat dicari nilai RGB dalam range yang sama. � Persamaan yang aplikatif tergantung pada nilai H. � Ada tiga sektor yang menarik, yang berhubungan dengan interval 120 o dalam pembagian warna primer. � ◦ Dimulai dengan perkalian H dengan 360 o, yang mengembalikan hue ke nilai aslinya dalam range [0 o, 360 o] Sektor RG (0 o ≤ H < 120 o) Sektor GB (120 o ≤ H < 240 o) H = H – 120 o Kemudian komponen RGB dihitung: R = I(1 – S) B = 3 I – (R + G) Sektor BR (240 o ≤ H ≤ 360 o) H = H – 240 o Komponen RGB dihitung dengan: G = I(1 – S) B = I(1 – S) G = 3 I – (R + B) R = 3 I – (G + B) 38

To Be Continued … Materi 4 – Pengolahan Citra dalam Domain Spasial dan Restorasi Citra ANY QUESTION ? 39