Transformarea graficelor funciei de gradul II Graficul funciei

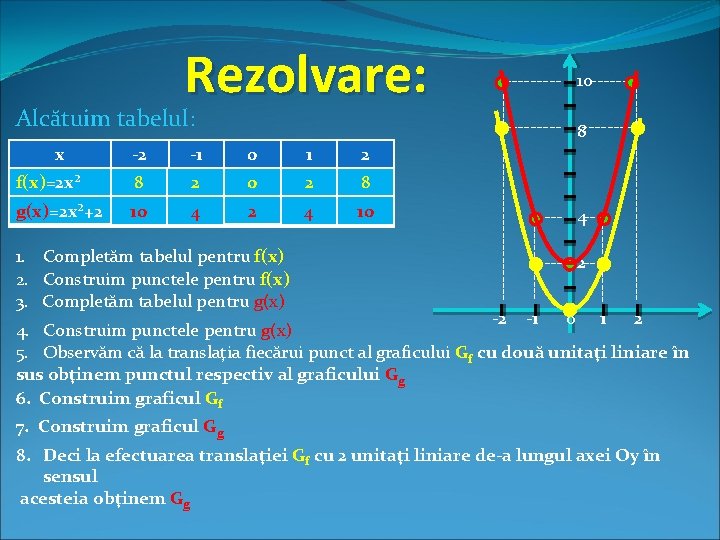
Transformarea graficelor funcţiei de gradul II Graficul funcţiei, f: R R, f(x)=ax²+n, a≠ 0, n∈R* Fie funcţia f: R R, f(x)=2 x². Trasaţi graficul funcţiei, g: R R, g(x)=2 x²+2

0 1 2 f(x)=2 x² 8 2 0 2 8 g(x)=2 x²+2 10 4 2 4 10 1. Completăm tabelul pentru f(x) 2. Construim punctele pentru f(x) 3. Completăm tabelul pentru g(x) ---- 4 --- ------ -1 ------ -2 ---- 2 --- -------------- 8 -------------- x ------- Alcătuim tabelul: ----- 10 ------- Rezolvare: -2 -1 0 1 2 4. Construim punctele pentru g(x) 5. Observăm că la translaţia fiecărui punct al graficului Gf cu două unitaţi liniare în sus obţinem punctul respectiv al graficului Gg 6. Construim graficul Gf 7. Construim graficul Gg 8. Deci la efectuarea translaţiei Gf cu 2 unitaţi liniare de-a lungul axei Oy în sensul acesteia obţinem Gg

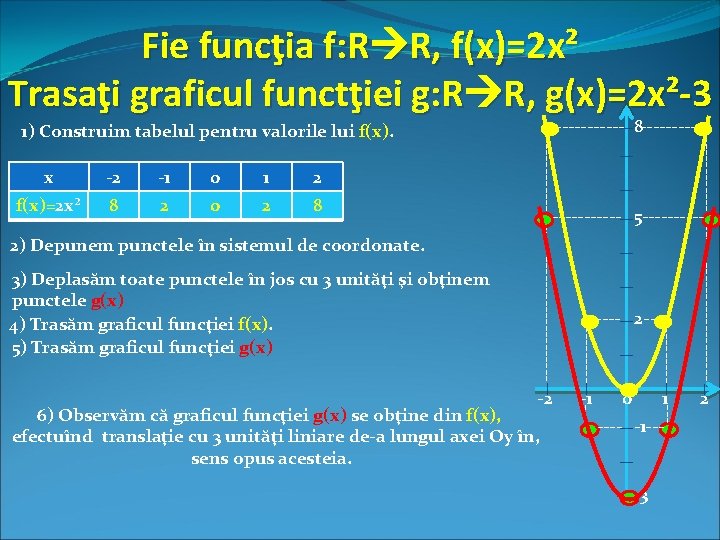
Fie funcţia f: R R, f(x)=2 x² Trasaţi graficul functţiei g: R R, g(x)=2 x²-3 8 2 0 2 8 2) Depunem punctele în sistemul de coordonate. 3) Deplasăm toate punctele în jos cu 3 unităţi şi obţinem punctele g(x) 4) Trasăm graficul funcţiei f(x). 5) Trasăm graficul funcţiei g(x) -2 -1 --------------------- f(x)=2 x² ----- 2 1 2 ------ 5 ----- 6) Observăm că graficul funcţiei g(x) se obţine din f(x), efectuînd translaţie cu 3 unităţi liniare de-a lungul axei Oy în, sens opus acesteia. 2 0 --- 1 ----- 0 --- -1 --------------------- -2 ----- x ------ 8 ------ 1) Construim tabelul pentru valorile lui f(x). ---- -1 --- -3

Generalizăm!!! Ce putem spune despre graficul funcţiei, f: R R, f(x)=ax²+n, a≠ 0, n∈R*? Graficul funcţiei f: R R, f(x)=ax²+n, a≠ 0, n∈R* este o parabola, care se obţine din graficul funcţiei g: R R, g(x)=ax², a≠ 0, efectuînd translaţia de-a lungul axei Oy cu n unităţi liniare în sensul acesteia dacă n>0 sau cu n unităţi liniare în sens opus acesteia, dacă n<0.

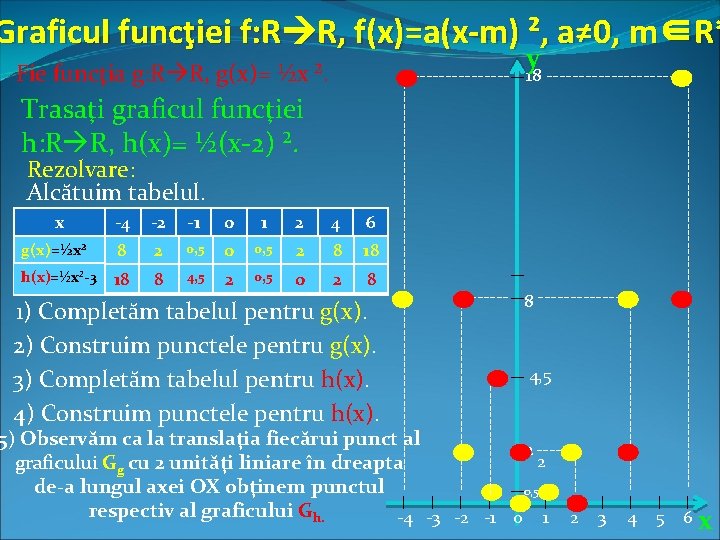
Graficul funcţiei f: R R, f(x)=a(x-m) ², a≠ 0, m∈R* -4 -2 -1 0 1 2 4 6 g(x)=½x² 8 2 0, 5 0 0, 5 2 8 18 h(x)=½x²-3 18 8 4, 5 2 0, 5 0 2 8 1) Completăm tabelul pentru g(x). 2) Construim punctele pentru g(x). 3) Completăm tabelul pentru h(x). 4) Construim punctele pentru h(x). -------------------------------- x ------- 8 ------------------ Rezolvare: Alcătuim tabelul. --------------- Trasaţi graficul funcţiei h: R R, h(x)= ½(x-2) ². -------------------------------- 4, 5 ----- 5) Observăm ca la translaţia fiecărui punct al 2 ---2 graficului Gg cu 2 unităţi liniare în dreapta de-a lungul axei OX obţinem punctul 0, 5 respectiv al graficului Gh. -4 -3 -2 -1 0 1 2 3 --------------- Fie funcţia g: R R, g(x)= ½x ². y 18 ----------- 4 5 6 x

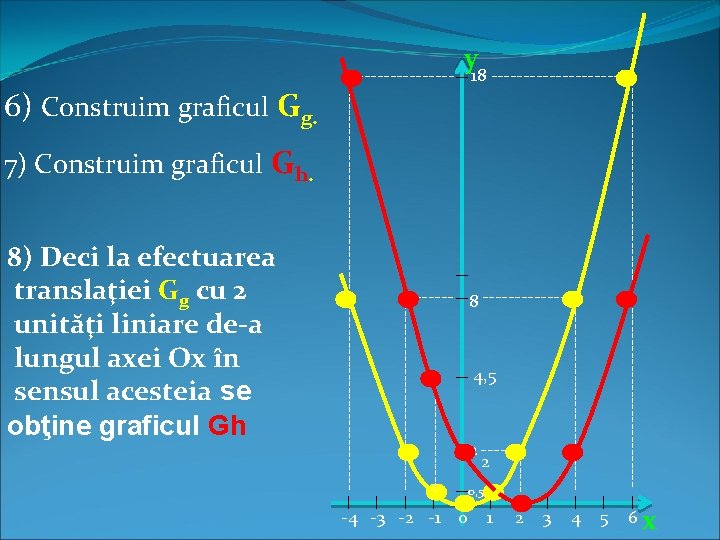
-4 -3 -2 -1 0 -------------------------------- ------- 8 ------- 4, 5 2 ---2 0, 5 1 ----- 8) Deci la efectuarea translaţiei Gg cu 2 unităţi liniare de-a lungul axei Ox în sensul acesteia se obţine graficul Gh --------- 7) Construim graficul Gh. --------------- 6) Construim graficul Gg. -------------------------------- y 18 ----------- 2 3 4 5 6 x

Generaliz ă m! Cum am putea obţine graficul funcţiei, f: R R, f(x)=a(x-m)², a≠ 0, m∈R*. Din graficul funcţiei g: R R, g(x)=ax², a≠ 0. Graficul funcţie f: R R, f(x)= a(x-m)², a≠ 0, m∈R*, este o parabola care se obţine din graficul funcţiei g: R R, g(x)=ax², a≠ 0, efectuînd translaţia de-a lungul axei Ox cu m unităţi liniare în sensul acesteia, dacă m>0, sau cu m unităţi liniare în sensul opus acesteia, dacă m<0.

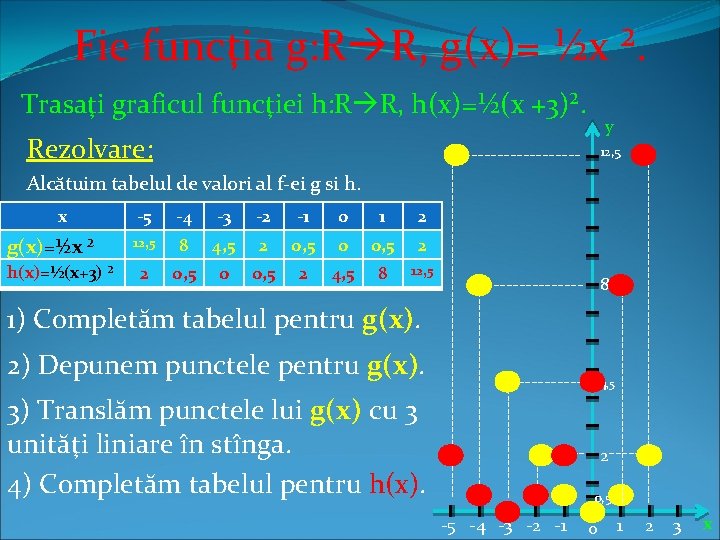
Fie funcţia g: R R, g(x)= ½x ². Trasaţi graficul funcţiei h: R R, h(x)=½(x +3)². -1 0 1 2 12, 5 8 4, 5 2 0, 5 0 0, 5 2 4, 5 8 12, 5 1) Completăm tabelul pentru g(x). 2) Depunem punctele pentru g(x). 3) Translăm punctele lui g(x) cu 3 unităţi liniare în stînga. 4) Completăm tabelul pentru h(x). -------- 8 -5 -4 -3 -2 -1 -------------------------------------------- -2 ------ -3 --------- h(x)=½(x+3) ² -4 ---------------- g(x)=½x ² -5 4, 5 2 ------ x 12, 5 ------ Alcătuim tabelul de valori al f-ei g si h. -------------------------- ------ Rezolvare: y 0, 5 0 1 2 3 x

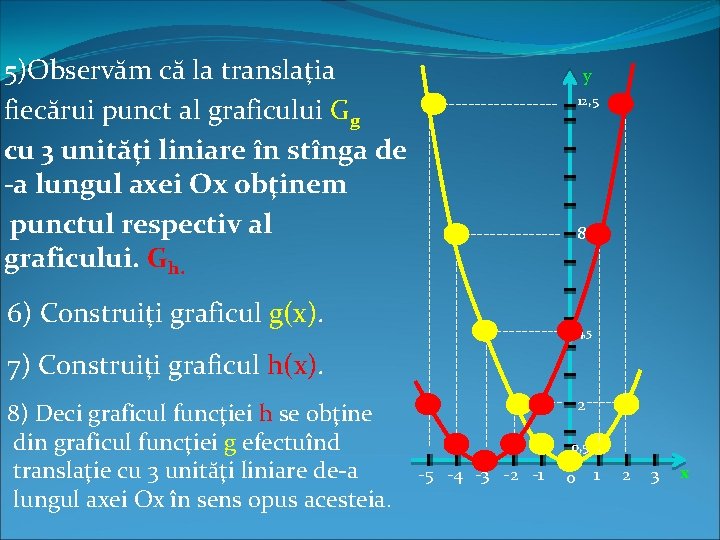
--------- -5 -4 -3 -2 -1 -------------------------------------------- 8 ------------------------------------------ 8) Deci graficul funcţiei h se obţine din graficul funcţiei g efectuînd translaţie cu 3 unităţi liniare de-a lungul axei Ox în sens opus acesteia. 12, 5 4, 5 2 ------ 7) Construiţi graficul h(x). ---------- 6) Construiţi graficul g(x). y ------ 5)Observăm că la translaţia fiecărui punct al graficului Gg cu 3 unităţi liniare în stînga de -a lungul axei Ox obţinem punctul respectiv al graficului. Gh. 0, 5 0 1 2 3 x

Vă doresc succes. . .