TRANSFORMAES E EVOLUES TCNICAS Os transportes TRANSFORMAES E

TRANSFORMAÇÕES E EVOLUÇÕES TÉCNICAS – Os transportes -

TRANSFORMAÇÕES E EVOLUÇÕES TÉCNICAS – Os transportes - Sociedade: üExploro a evolução de transportes com novas oportunidades e novos problemas das sociedades contemporâneas üCompreender as consequências sociais da evolução dos transportes exº mutação dos espaços. . globalização

TRANSFORMAÇÕES E EVOLUÇÕES TÉCNICAS – Os transportes - Tecnologia: Actuo nas utilizações de equipamentos e sistemas técnicos tendo em conta a sua evolução tecnológica no sentido da melhoria de rendimento, da redução do número de horas por tarefa, etc. üOs diferentes meios de propulsão usados em transportes públicos e privados ao longo dos tempo ( o vento. . o vapor de água … motor a diesel…. ) üRelacionar a evolução dos sistemas de propulsão com a necessidade de obter maior desempenho, mas ao mesmo tempo diminuir os níveis de poluição.

MEIOS DE PROPULSÃO O vento Tracção animal O vapor de água

Meio de propulsão – motores a gasolina, gasóleo, ….

TRANSFORMAÇÕES E EVOLUÇÕES TÉCNICAS – Os transportes - Ciência: Actuo face às transformações e evoluções técnicas dos equipamentos relacionando-as com a evolução histórica dos princípios científicos, com especial ênfase nas ciências físicas e químicas, suportada pela evolução da própria matemática ao nível do cálculo diferencial. ü As características dos movimentos: rectilíneos uniformes, variados (acelerados, retardados) e circulares. ü Aplicar as definições de posição, velocidade/ velocidade média, aceleração, força centrífuga, força centripeta e força de atrito à descrição dos movimentos üReconhecer o papel das várias grandezas físicas na descrição dos movimentos reais ü Aplicar a novas situações os conhecimentos adquiridos

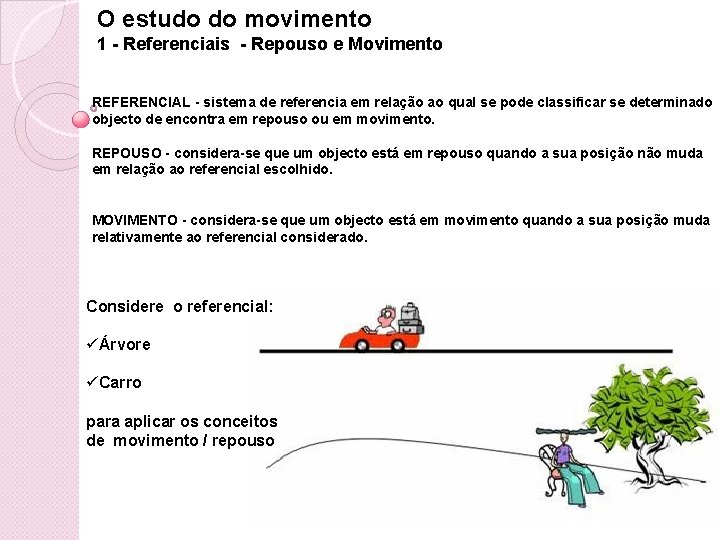
O estudo do movimento 1 - Referenciais - Repouso e Movimento REFERENCIAL - sistema de referencia em relação ao qual se pode classificar se determinado objecto de encontra em repouso ou em movimento. REPOUSO - considera-se que um objecto está em repouso quando a sua posição não muda em relação ao referencial escolhido. MOVIMENTO - considera-se que um objecto está em movimento quando a sua posição muda relativamente ao referencial considerado. Considere o referencial: üÁrvore üCarro para aplicar os conceitos de movimento / repouso

- Trajectórias – ü Linhas definidas pelas sucessivas posições ocupadas pela partícula em movimento Rectilínea Curvilínea

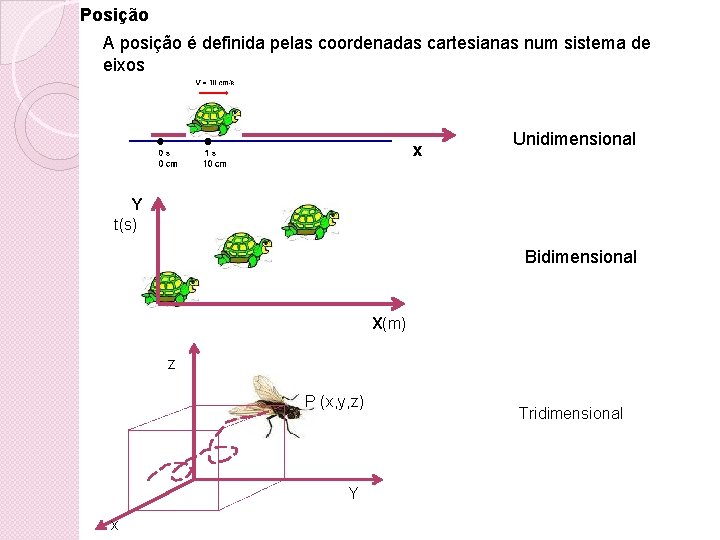
Posição A posição é definida pelas coordenadas cartesianas num sistema de eixos x Unidimensional Y t(s) Bidimensional X(m) z P (x, y, z) Y x Tridimensional

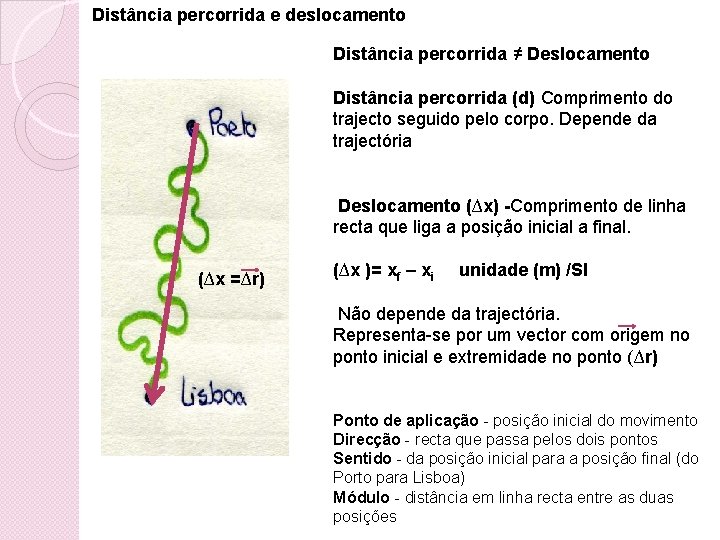
Distância percorrida e deslocamento Distância percorrida ≠ Deslocamento Distância percorrida (d) Comprimento do trajecto seguido pelo corpo. Depende da trajectória Deslocamento (∆x) -Comprimento de linha recta que liga a posição inicial a final. (∆x =∆r) (∆x )= xf – xi unidade (m) /SI Não depende da trajectória. Representa-se por um vector com origem no ponto inicial e extremidade no ponto (∆r) Ponto de aplicação - posição inicial do movimento Direcção - recta que passa pelos dois pontos Sentido - da posição inicial para a posição final (do Porto para Lisboa) Módulo - distância em linha recta entre as duas posições

Variação do tempo ou intervalo de tempo - diferença entre o instante final e o inicial. Unidades - segundo (s) - Sistema Internacional Rapidez média / celeridade média - a razão entre o espaço percorrido e o intervalo de tempo ∆d Rm = ______ ∆t Unidades - metro por segundo (m/s) - Sistema Internacional Velocidade média - a razão entre o deslocamento efectuado e o intervalo de tempo Unidades - metro por segundo (m/s) - Sistema Internacional

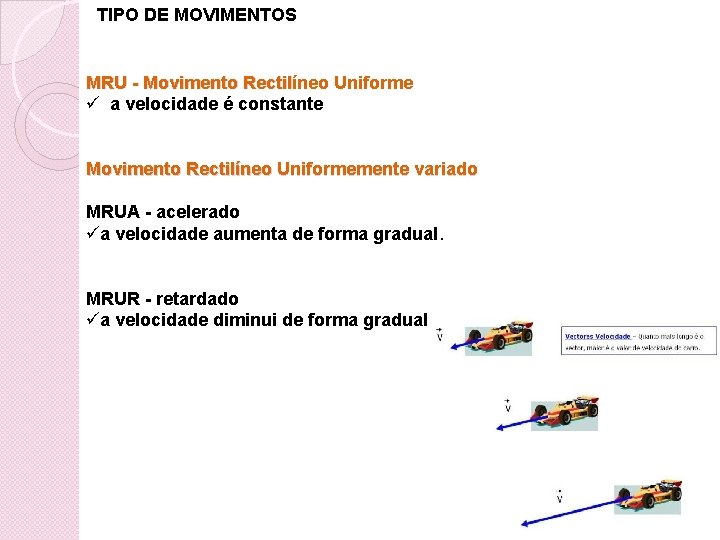
TIPO DE MOVIMENTOS MRU - Movimento Rectilíneo Uniforme ü a velocidade é constante Movimento Rectilíneo Uniformemente variado MRUA - acelerado üa velocidade aumenta de forma gradual. MRUR - retardado üa velocidade diminui de forma gradual.

MRU - Movimento Rectilíneo Uniforme O movimento rectilíneo uniforme consiste num movimento de um corpo qualquer que se desloca percorrendo espaços iguais em tempos iguais em linha recta, ou seja, com aceleração nula e velocidade constante em módulo, direcção e sentido. v = d t unidade (m/s) /SI t = ? t =1 h

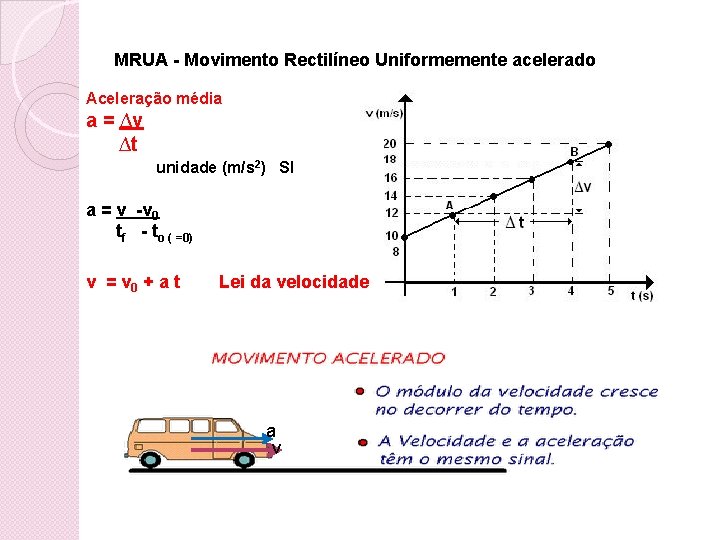
MRUA - Movimento Rectilíneo Uniformemente acelerado Aceleração média a = ∆v ∆t unidade (m/s 2) SI a = v -v 0 tf - to ( =0) v = v 0 + a t Lei da velocidade a v

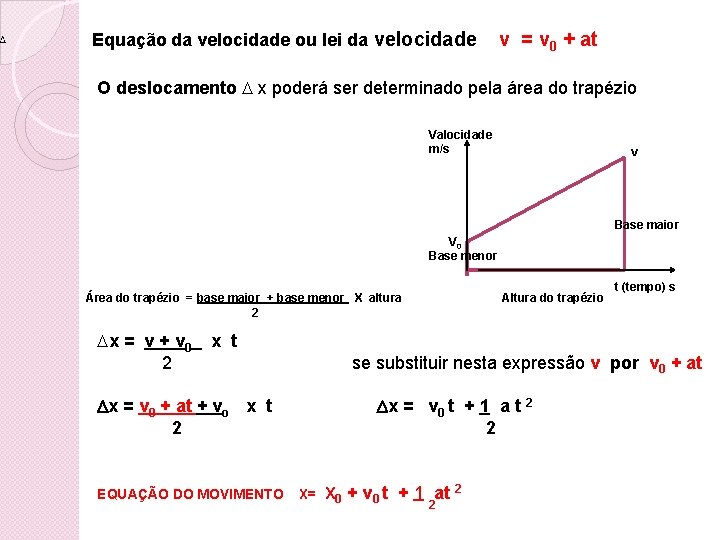
Equação da velocidade ou lei da velocidade v = v 0 + at O deslocamento x poderá ser determinado pela área do trapézio Valocidade m/s v Base maior V 0 Base menor Área do trapézio = base maior + base menor X altura 2 Altura do trapézio t (tempo) s x = v + v 0 x t 2 se substituir nesta expressão v por v 0 + at x = v 0 + at + vo x t x = v 0 t + 1 a t 2 2 EQUAÇÃO DO MOVIMENTO X= X 0 + v 0 t + 1 at 2 2

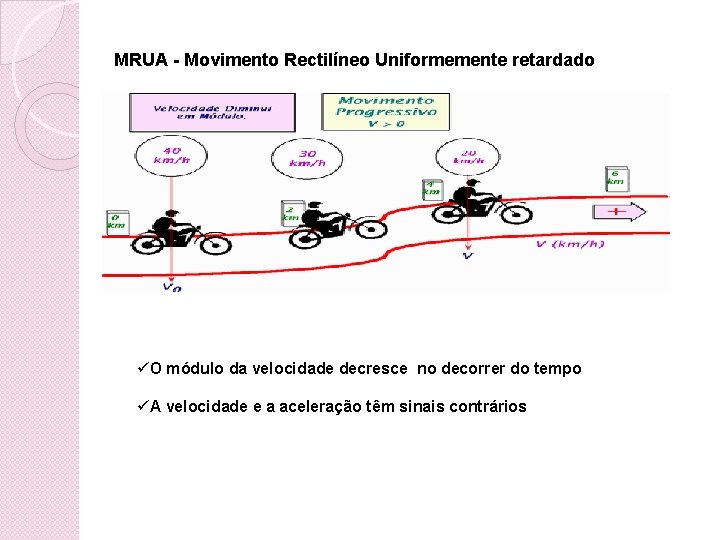
MRUA - Movimento Rectilíneo Uniformemente retardado üO módulo da velocidade decresce no decorrer do tempo üA velocidade e a aceleração têm sinais contrários

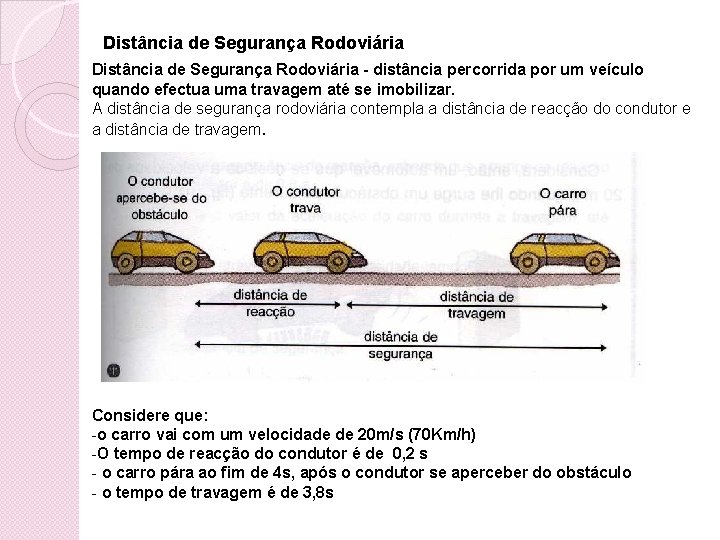
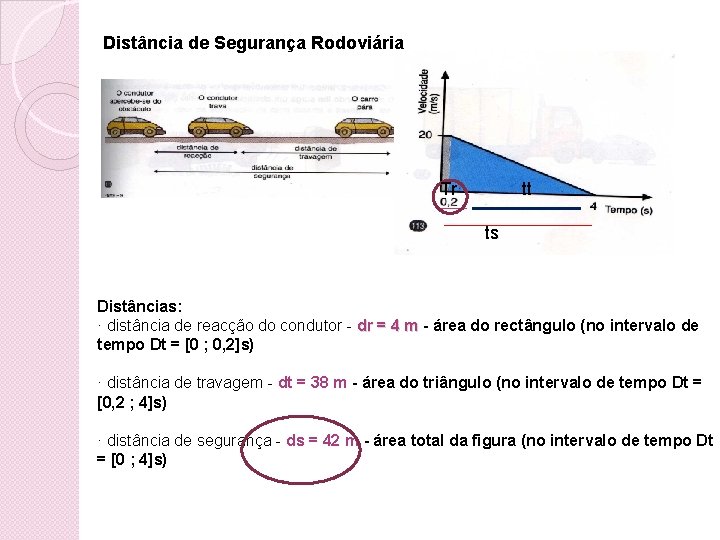
Distância de Segurança Rodoviária - distância percorrida por um veículo quando efectua uma travagem até se imobilizar. A distância de segurança rodoviária contempla a distância de reacção do condutor e a distância de travagem. Considere que: -o carro vai com um velocidade de 20 m/s (70 Km/h) -O tempo de reacção do condutor é de 0, 2 s - o carro pára ao fim de 4 s, após o condutor se aperceber do obstáculo - o tempo de travagem é de 3, 8 s

Distância de Segurança Rodoviária Tr tt ts Distâncias: · distância de reacção do condutor - dr = 4 m - área do rectângulo (no intervalo de dr = 4 m tempo Dt = [0 ; 0, 2]s) · distância de travagem - dt = 38 m - área do triângulo (no intervalo de tempo Dt = [0, 2 ; 4]s) · distância de segurança - ds = 42 m - área total da figura (no intervalo de tempo Dt = [0 ; 4]s)

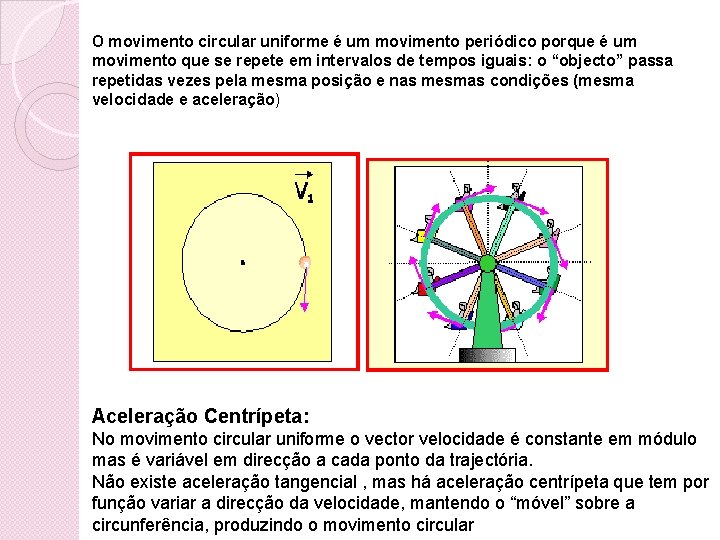
MOVIMENTO CIRCULAR UNIFORME Um “objecto” está em movimento circular uniforme quando a sua trajectória é circular e o módulo de sua velocidade permanece constante. No dia a dia , vemos muitos exemplos de movimento circular uniforme :

O movimento circular uniforme é um movimento periódico porque é um movimento que se repete em intervalos de tempos iguais: o “objecto” passa repetidas vezes pela mesma posição e nas mesmas condições (mesma velocidade e aceleração) Aceleração Centrípeta: No movimento circular uniforme o vector velocidade é constante em módulo mas é variável em direcção a cada ponto da trajectória. Não existe aceleração tangencial , mas há aceleração centrípeta que tem por função variar a direcção da velocidade, mantendo o “móvel” sobre a circunferência, produzindo o movimento circular

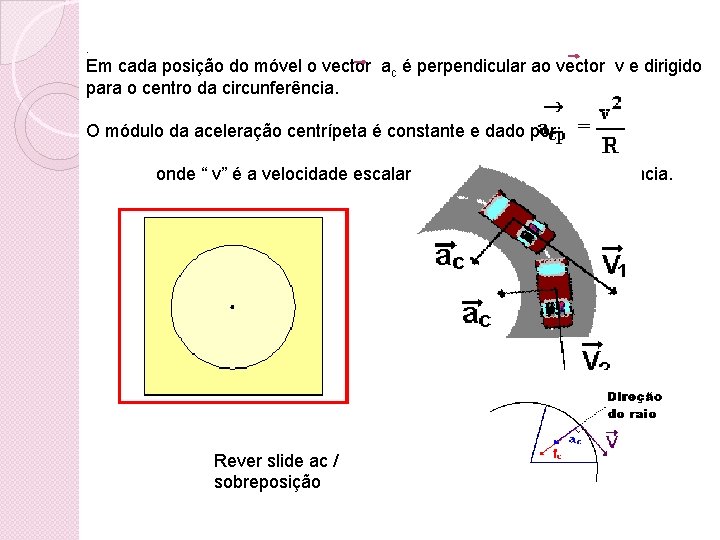
. Em cada posição do móvel o vector ac é perpendicular ao vector v e dirigido para o centro da circunferência. O módulo da aceleração centrípeta é constante e dado por: onde “ v” é a velocidade escalar e “ R” é o raio da circunferência. Rever slide ac / sobreposição

PERÍODO E FREQUÊNCIA de um MCU O intervalo de tempo necessário para que o movimento volte a ter as mesmas características dá-se o nome de período T Exº Relógio. . O ponteiro leva 60 s a cumprir uma volta Frequência (f) : É o número de voltas (n) que o móvel realiza na unidade de tempo ( em cada segundo , em cada minuto , em cada hora ). É dada pela relação : f = T No SI a unidade de frequência é o hertz e se abrevia por hz. 1 rps =1 hz 2 rps = 2 h e assim por diante. . . "O período é o inverso da frequência e a frequência é o inverso do período. "

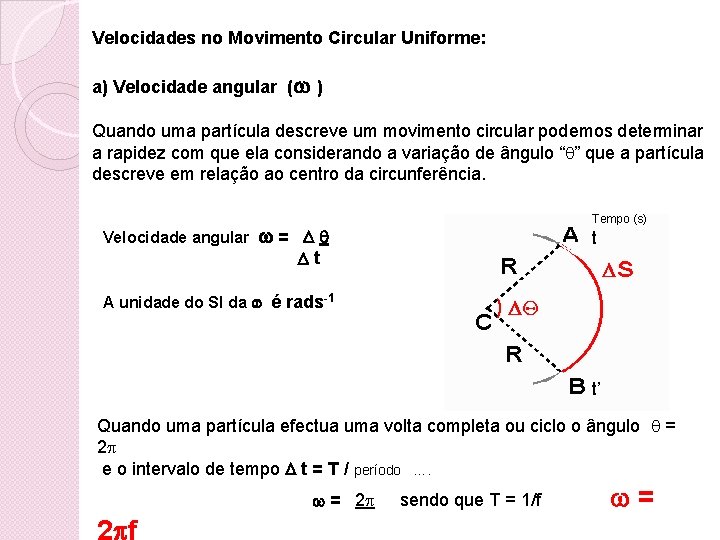
Velocidades no Movimento Circular Uniforme: a) Velocidade angular ( ) Quando uma partícula descreve um movimento circular podemos determinar a rapidez com que ela considerando a variação de ângulo “ ” que a partícula descreve em relação ao centro da circunferência. Velocidade angular = Tempo (s) t t A unidade do SI da é rads-1 t’ Quando uma partícula efectua uma volta completa ou ciclo o ângulo = 2 e o intervalo de tempo t = T / período …. = 2 sendo que T = 1/f = 2 f

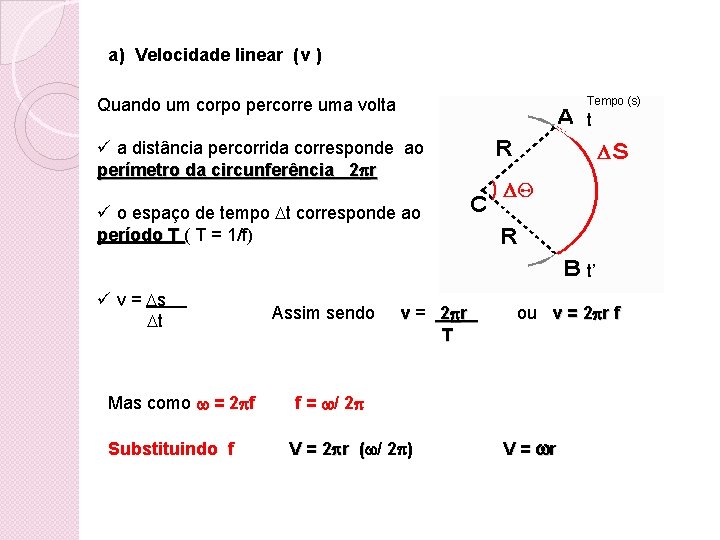
a) Velocidade linear (v ) Quando um corpo percorre uma volta Tempo (s) t ü a distância percorrida corresponde ao perímetro da circunferência 2 r ü o espaço de tempo t corresponde ao período T ( T = 1/f) período T t’ ü v = s t Assim sendo v = 2 r ou v = 2 r f r T Mas como = 2 f f = / 2 Substituindo f V = 2 r ( / 2 ) V = r r (

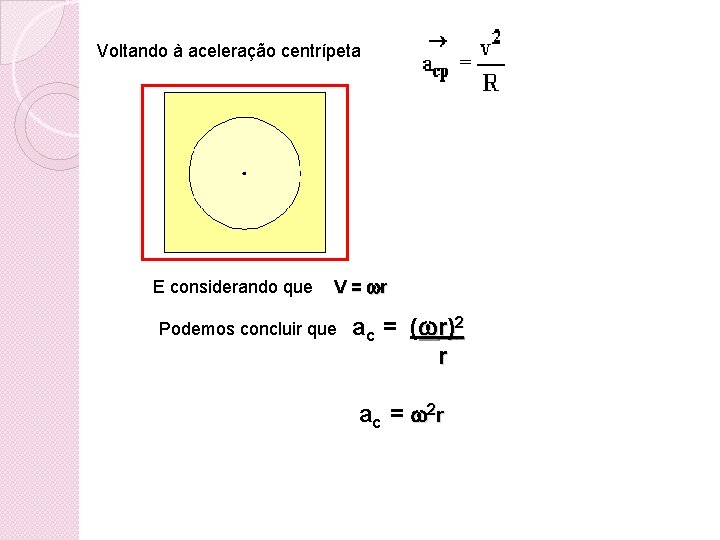
Voltando à aceleração centrípeta E considerando que V = r Podemos concluir que ac = ( r)2 r ac = 2 r

FIM